38. Затяжной прыжок с парашютом

Противоречие объясняется тем, что падение с нераскрытым парашютом ошибочно принято было за свободное, не замедляемое сопротивлением воздуха. Между тем оно существенно отличается от падения в несопротивляющейся среде.

Попробуем установить, хотя бы приблизительно, подлинную картину падения при затяжном прыжке. Будем пользоваться для расчетов следующей найденной из опыта приближенной формулой для величины f сопротивления воздуха при рассматриваемых условиях:

f = 0,03 v² кг,

где v – скорость падения в метрах в секунду. Сопротивление, как видим, пропорционально квадрату скорости; а так как парашютист падает с возрастающей скоростью, то наступает момент, когда сила сопротивления делается равной весу тела. С этого момента скорость падения расти больше не будет; падение из ускоренного становится равномерным.

Для парашютиста это наступает тогда, когда его вес (вместе с парашютом) сделается равным 0,03v²; принимая вес снаряженного парашютиста в 90 кг, имеем уравнение

0,03v² = 90,

откуда v = 55 м/с.

Итак, парашютист падает ускоренно лишь до тех пор, пока не накопит скорости 55 м/с. Это наибольшая скорость, с какою он опускается, в дальнейшем скорость уже не возрастает. Определим – опять приближенно – сколько секунд употребил парашютист для достижения этой максимальной скорости. Примем во внимание, что в самом начале падения, пока скорость мала, сопротивление воздуха ничтожно, и тело падает как свободное, т. е. с ускорением 9,8 м/с. К концу же интервала ускоренного движения, когда устанавливается равномерное падение, ускорение равно нулю. Для нашего приближенного расчета можно допустить, что ускорение в среднем равнялось

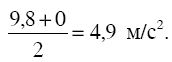
Если принять таким образом, что секундная скорость нарастала на 4,9 м в секунду, то она достигает величины 55 м по истечении

55: 4,9 = 11 с.

Путь 5, проходимый телом в 11 секунд такого ускоренного движения, равен

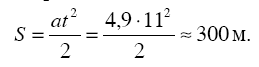
Теперь выясняется подлинная картина падения Евдокимова. Первые 11 с он падал с постепенно уменьшающимся ускорением, пока не накопил скорости 55 м/с, приблизительно на 300-м метре пути. Остальной путь затяжного прыжка он проходил равномерным движением со скоростью 55 м/с. Равномерное движение, согласно нашему приближенному расчету, длилось

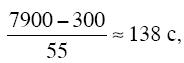
а весь затяжной прыжок

11 + 138 = 149 с,

что мало отличается от действительной продолжительности (142 с).

Сделанный нами элементарный расчет надо рассматривать лишь как первое приближение к действительности, так как он основан на ряде упрощающих допущений.

Приведем для сравнения данные, полученные путем опыта: при весе снаряженного парашютиста 82 кг максимальная скорость устанавливается на 12-й секунде, когда парашют опускается на 425–460 м (Забелин, М. Прыжок с парашютом. М., 1933).