ТЕХНОЛОГИИ. ЧТО ДАЛЬШЕ?

ТЕХНОЛОГИИ. ЧТО ДАЛЬШЕ?

Мы закончили вводное путешествие в мир малых расстояний, доступных человеку при нынешнем уровне развития технологий. Однако границы исследовательских возможностей человека не могут ограничивать природу реальности. Пусть сегодня кажется, что нам трудно придумать и изготовить технические средства, позволяющие напрямую исследовать еще более мелкие размеры и расстояния, мы все же можем попытаться сделать некоторые выводы о структуре и взаимодействиях на них при помощи математических аргументов.

Мы признаем, что без экспериментальных данных невозможно точно определить, что существует на тех невообразимо малых масштабах, в которых нам тоже очень хотелось бы разобраться. Тем не менее даже в отсутствие измерений у нас остаются теоретические рассуждения, способные направить наши усилия и подкрепить догадки о том, как вещество и силы природы могут вести себя на еще более мелких масштабах. Мы можем поискать на доступных нам масштабах новые возможности — средства и способы, которые помогли бы объяснить и соотнести между собой наблюдаемые явления, даже если их фундаментальные компоненты недоступны для непосредственных наблюдений.

Мы пока еще не знаем, какие из наших теоретических построений окажутся верными. Но даже без непосредственного экспериментального доступа к самым маленьким расстояниям можно сказать точно: то, что нам удалось наблюдать, серьезно ограничивает спектр явлений, которые в принципе могут быть обнаружены — ведь именно фундаментальная теория в итоге должна объяснить все, что мы видим. А значит, экспериментальные результаты даже на более крупных расстояниях ограничивают спектр возможностей и заставляют нас рассуждать в определенных, достаточно конкретных направлениях.

Кое?кто даже предполагает, что между энергиями БАКа и еще более высокими энергиями, действующими на еще более маленьких расстояниях, существует пустыня, то есть некий промежуток, практически лишенный значимых расстояний или энергий. Вероятно, подобные теории возникают от недостатка воображения или данных. Но многие ученые считают, что следующие по–настоящему интересные открытия на сверхмалых масштабах должны быть связаны с унификацией всех физических взаимодействий на малых расстояниях.

Эта концепция способна распалить воображение как ученых, так и обычных людей. Согласно такому сценарию мир, который мы видим вокруг, пока не раскрывает нам фундаментальную, очень красивую и простую теорию, лежащую в основе всего на свете, которая охватывает все известные физические взаимодействия (или, по крайней мере, все взаимодействия, кроме гравитации). С того самого момента, когда ученые впервые поняли, что сил в природе больше, чем одна, множество физиков посвятило свою жизнь поиску единой теории.

Одно из самых интересных рассуждений на эту тему представили Говард Джорджи и Шелдон Глэшоу в 1974 г. Они предположили, что, хотя мы наблюдаем при низких энергиях три негравитационных взаимодействия, в которых фигурируют различные силы (электромагнитные, а также слабые и сильные ядерные), при гораздо более высоких энергиях останется лишь одно взаимодействие, одна сила (рис. 19)[23]. Эта сила охватывает все три известных типа взаимодействия (сильное, слабое и электромагнитное). Данное теоретическое построение получило название теории великого объединения (GUT — Grand Unified Theory).

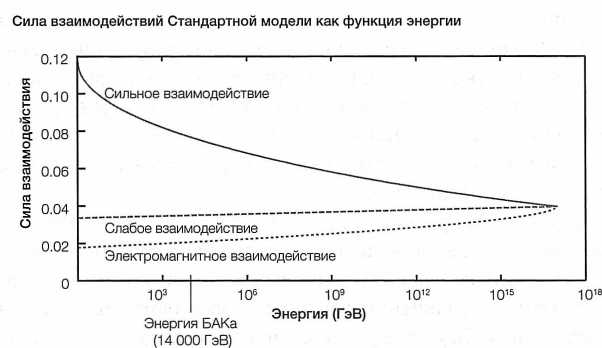
РИС. 19. При высоких энергиях три известных негравитационных взаимодействия могут иметь одинаковую силу, и не исключено, что их можно было бы свести в одно взаимодействие

Возможность того, что силы всех трех взаимодействий действительно сходятся в одной точке, представляется не просто красивой гипотезой. Расчеты с использованием квантовой механики и специальной теории относительности указывают: дело, вполне возможно, обстоит именно так[24]. Однако энергетический диапазон, в котором это происходит, намного превышает все те энергии, которые мы можем изучать в своих экспериментах на коллайдере. Расстояния, на которых согласно расчетам должно «работать» единое взаимодействие, составляют порядка 10^-30см. Но, несмотря на то что подобные расстояния выходят далеко за пределы наших возможностей по непосредственному наблюдению, мы можем подумать о том, какие косвенные следствия унификации взаимодействий можно было бы зарегистрировать имеющимися средствами.

Одним из таких явлений мог бы стать распад протона. Согласно теории Джорджи и Глэшоу — а она попутно вводит новые виды взаимодействий между кварками и лептонами — протоны должны самопроизвольно распадаться. Учитывая достаточно специфическую природу этой теории, ученые смогли подсчитать, с какой частотой должен происходить этот распад. До сих пор никому не удалось его наблюдать, что, по идее, исключает вариант теории, предложенный Джорджи и Глэшоу. Это не означает, однако, что теория великого объединения обязательно неверна. Просто в реальности она может оказаться более сложной, чем предположили эти ученые.

Теория великого объединения наглядно демонстрирует, как можно расширить наши знания за пределами непосредственно наблюдаемых размеров. Пользуясь теоретическими допущениями, мы можем попытаться экстраполировать то, что уже сумели экспериментально проверить, на область пока недоступных прямому измерению энергий. В случае теории великого объединения попытки экспериментально наблюдать распад протона позволили ученым косвенно изучить взаимодействия на расстояниях, выходящих далеко за пределы возможностей непосредственного наблюдения. Эти эксперименты позволили проверить выдвинутое предположение. Приведенный пример показывает, что иногда нам удается сделать интересные заключения о свойствах вещества и фундаментальных взаимодействиях и даже придумать способы распространить выводы, основанные на экспериментальных данных, на гораздо более высокие энергии и более общие классы явлений при помощи рассуждений о расстояниях и масштабах, которые на первый взгляд представляются слишком далекими, чтобы принимать их во внимание. Следующая (и последняя) остановка нашего воображаемого путешествия — так называемая планковская длина, а именно 10^-33 см. Чтобы получить некоторое представление о том, насколько реально мала эта величина, представьте, что она настолько же меньше протона, насколько сам протон меньше… ну, к примеру, Род–Айленда. В этом масштабе даже самые фундаментальные наши представления о пространстве и времени, вероятно, окажутся неверными. Мы не представляем даже, как мог бы выглядеть гипотетический эксперимент по исследованию расстояний, меньших, чем планковская длина. Это самый маленький размер, какой мы в принципе можем вообразить.

Тот факт, что мы не можем даже представить эксперимент, при помощи которого можно было бы исследовать планковские расстояния, вполне может оказаться не просто симптомом ограниченности человеческого воображения, техники или даже финансирования. Недоступность расстояний, меньших, чем планковская длина, может оказаться подлинным ограничением, обусловленным законами природы. Как мы убедимся в следующей главе, из законов квантовой механики следует, что для зондирования малых расстояний необходимы высокие энергии. Но стоит энергии, заключенной в небольшом объеме, оказаться слишком большой, как вещество коллапсирует и образуется черная дыра. В этот момент на передний план выходит гравитация. Дополнительная энергия лишь сделает черную дыру еще больше, в чем мы успели уже убедиться на примере ситуаций, в которых влияние законов квантовой механики невелико. Мы не знаем, как вообще можно исследовать расстояние, уступающее планковской длине. Дополнительная энергия здесь не поможет. Вероятно, что на этих невообразимо крошечных расстояниях традиционные представления о пространстве уже неприменимы.

Мне недавно довелось читать лекцию. После того как я рассказала о нынешнем состоянии физики элементарных частиц и наших предположениях о природе дополнительных измерений, кто?то из слушателей процитировал мне мое собственное забытое заявление о возможных ограничениях наших представлений о пространстве–времени. Меня спросили, как можно совместить рассуждения о дополнительных измерениях с мыслью о том, что на каких?то расстояниях пространство–время просто не существует.

Вообще, рассуждения о том, что категории пространства и времени теряют свою актуальность в определенных условиях, относятся лишь к невообразимо малой планковской длине. Поскольку никто до сих пор не видел объектов размером меньше 10^-17см, можно сказать, что классическая геометрия на измеримых расстояниях не нарушается. Даже если понятие пространства на расстояниях, сравнимых с планковской длиной, теряет актуальность, не стоит забывать, что речь здесь идет о расстояниях много меньших, чем все, что мы до сих пор исследовали. Здесь нет никакого противоречия, если предположить, что при усреднении на много больших наблюдаемых расстояниях возникает узнаваемая структура. В конце концов, на разных масштабах вещество нередко ведет себя очень по–разному. Эйнштейн говорил о непрерывной геометрии пространства на больших расстояниях. Однако его мысли могут оказаться неверными на малых расстояниях, если, конечно, они пренебрежимо слабо влияют на явления, наблюдаемые на измеримых расстояниях, так что добавление еще нескольких фундаментальных ингредиентов не даст различимого эффекта, который мы могли бы зарегистрировать.

Независимо от того, существуют ли на самых малых расстояниях пространство и время, принципиальное свойство планковской длины, о котором сообщают нам уравнения, состоит в том, что гравитация, действие которой на фундаментальные частицы на измеримых расстояниях пренебрежимо мало, становится серьезной силой, сравнимой по интенсивности с остальными известными нам силами. На планковской длине стандартная формула тяготения, согласно теории относительности Эйнштейна, уже неприменима. В отличие от более крупных расстояний, где мы можем предсказать поведение системы таким образом, чтобы оно хорошо согласовывалось с экспериментальными данными, на этих крохотных расстояниях квантовая механика и теория относительности несостоятельны и применять теории, которым мы обычно пользуемся, невозможно. Мы даже не знаем, как подойти к прогнозированию. Общая теория относительности основана на классической пространственной геометрии. На планковской длине категории пространства и времени из?за квантовых флуктуаций может образовать слишком сложную структуру, к которой уже неприложимы традиционные формулы тяготения.

Чтобы делать какие бы то ни было предсказания о планковских расстояниях, нам необходимо обзавестись новой концептуальной теорией, объединяющей квантовую механику и гравитацию в единую теорию, известную как теория квантовой гравитации. Законы природы, наиболее эффективно работающие на планковских расстояниях, должны сильно отличаться от тех, которые уже доказали свою справедливость на доступных нашему наблюдению масштабах. Не исключено, что для понимания планковского масштаба понадобится не менее фундаментальный сдвиг парадигмы, чем переход от классической механики к квантовой. Пусть мы не можем производить измерения на самых крохотных расстояниях, но у нас есть шанс больше узнать о фундаментальной теории гравитации, пространстве и времени при помощи все более сложных теоретических построений.

Самый популярный кандидат на роль «теории всего» — так называемая теория струн. Первоначально в ней речь шла о том, что на определенных масштабах фундаментальные частицы заменяются на фундаментальные струны. Сегодня нам известно, что в теории струн помимо собственно струн фигурируют и другие фундаментальные объекты (в главе 17 мы узнаем об этом больше), а ее название иногда заменяют на более широкое (но менее определенное) — М–теория. В настоящее время эта теория — самое многообещающее направление исследований квантовой гравитации.

Однако теория струн ставит перед исследователями громадные концептуальные и математические проблемы. Никто пока не знает, как сформулировать теорию струн, чтобы ответить на все вопросы, с которым должна иметь дело теория квантовой гравитации. Более того, размеры струн порядка 10^_33 см, скорее всего, неподвластны экспериментам.

Поэтому возникает резонный вопрос: стоит ли тратить время и ресурсы на исследования в области теории струн? Мне очень часто задают этот вопрос. Зачем изучать теорию, из которой вряд ли следует хоть что?нибудь, что можно проверить экспериментально? Некоторые физики считают, что достаточным основанием для этого является математическая и теоретическая непротиворечивость теории. Эти люди надеются повторить успех Эйнштейна, которому удалось разработать общую теорию относительности на основе почти исключительно теоретических и математических построений.

Другим мотивом к изучению теории струн — мотивом, который лично мне представляется очень важным — является то, что она позволяет нам по–новому взглянуть на идеи, следствия из которых могут проявляться и на измеримых расстояниях. Приведем две такие идеи: это суперсимметрия и теории дополнительных измерений, о которых мы тоже поговорим в главе 17. В физике элементарных частиц эти теории имеют экспериментальные следствия. Более того, если некоторые теории, связанные с дополнительными измерениями, подтвердятся и смогут объяснить явления, наблюдаемые на энергиях БАКа, то можно будет рассчитывать на получение данных по теории струн тоже на гораздо более низких энергиях, чем считается в настоящий момент. Открытие суперсимметрии или дополнительных измерений само по себе не докажет теорию струн, но это будет сильный аргумент в пользу работы над абстрактными идеями, у которых нет прямых экспериментально проверяемых следствий.

Данный текст является ознакомительным фрагментом.