7.7. Опасный астероид (99942) Апофис

We use cookies. Read the Privacy and Cookie Policy

7.7. Опасный астероид (99942) Апофис

7.7.1. История обнаружения и исследования астероида Апофис. Несколько следующих подразделов посвящены результатам исследования движения потенциально опасного астероида Апофис с применением описанных выше методов.

Данный астероид, получивший предварительное обозначение 2004 MN4, был открыт в обсерватории Китт Пик (штат Аризона, США) 19 июня 2004 г. в ходе регулярных наблюдений, проводившихся там по программе поиска тел, сближающихся с Землей. Было получено шесть наблюдений астероида в течение двух ночей, после чего он фактически был потерян. 18 декабря того же года этот астероид был случайно переоткрыт Г. Гарраддом в Австралии, выполнявшим наблюдения по программе обзора астероидов в обсерватории Сайдинг Спринг. На этот раз наблюдения были продолжены во многих обсерваториях, что дало Центру малых планет возможность уже 20 декабря опубликовать Электронный циркуляр c орбитой астероида, найденной на основе 31 наблюдения, выполненного с июня по декабрь. 2004 MN4 оказался астероидом, сближающимся с Землей, движущимся по орбите, внутренней по отношению к земной и мало наклоненной к ней. Минимальное расстояние его орбиты от орбиты Земли составило всего 0,002 а.е. Абсолютная звездная величина астероида была оценена как 19,3m, что при характерных для данного типа астероидов альбедо соответствовало диаметру около 400 м. Малость межорбитального расстояния и размеры астероида дали основание классифицировать его как потенциально опасный для Земли.

В течение ближайших трех дней после повторного открытия астероида сразу две автоматические системы SENTRY в США и CLOMON 2 в Италии нашли, что астероид будет иметь очень тесное сближение с Землей 13 апреля 2029 г. Первоначальные оценки вероятности его столкновения с Землей в 2029 г. составляли около одной трехсотой, причем по мере увеличения числа используемых для уточнения орбиты наблюдений вероятность столкновения только возрастала. К 26 декабря по 169 наблюдениям вероятность оценивалась уже как 2,2 %, а к 27 декабря по 176 наблюдениям — как 3,3 %. Напряженность ситуации нарастала. Столкновение Земли с астероидом таких размеров угрожало региональной катастрофой.

К счастью, к вечеру 27 декабря в обсерватории Китт Пик были обнаружены шесть слабых изображений астероида 2004 MN4, полученных по иной программе наблюдений в марте 2004 г. и ранее остававшихся незамеченными. Расширение интервала времени, охваченного наблюдениями, позволило значительно увеличить точность предсказаний и по существу исключить возможность столкновения Земли с данным астероидом в 2029 г. Тем не менее, астероид продолжал интенсивно наблюдаться. В конце января 2005 г. в радиообсерватории Аресибо (Пуэрто-Рико) была проведена серия из пяти радиолокационных наблюдений астероида, позволивших существенно уточнить элементы его орбиты и с большей достоверностью прогнозировать его движение в будущем. Еще два радарных наблюдения астероида были выполнены 7 августа 2005 г. и 6 мая 2006 г. Всего на интервале с 15 марта 2004 г. по 16 августа 2006 г., по данным Центра малых планет, было выполнено 996 наблюдений, в том числе 989 наблюдений прямого восхождения и склонения и семь радарных наблюдений: два наблюдения запаздывания отраженного сигнала и пять наблюдений доплеровского сдвига частоты (http://ssd.jpl.nasa.gov/?radar).

Как оказалось, астероид пройдет мимо Земли 13 апреля 2029 г. на расстоянии даже меньшем, чем это ранее предполагалось: от центра Земли оно составит немного более 38 000 км — меньше высоты полета геостационарных спутников. На ночной половине Земли астероид можно будет наблюдать как звезду 3,3m. Для землян столь близкое прохождение небесного тела само по себе мало чем опасно. Однако опасными могут оказаться его последствия. Для астероида сближение с Землей обернется большим или меньшим изменением элементов орбиты под влиянием возмущения со стороны гравитационного поля планеты. Величина возмущений существенно зависит от минимального расстояния до астероида. К сожалению, сегодня это расстояние может быть рассчитано недостаточно точно. Отсюда возникает некоторая неопределенность прогноза дальнейшего движения астероида. В любом случае значительно изменится большая полуось его орбиты, или, другими словами, его среднее движение. Орбита астероида из внутренней по отношению к Земле (орбиты типа Атона, выходящей за пределы орбиты Земли только в окрестности афелия) превратится в орбиту типа Аполлона, с большой полуосью, превышающей 1 а.е., и подходящую к Солнцу ближе орбиты Земли в окрестности своего перигелия. Орбитальный период, который в настоящее время равен 0,89 года, превысит величину одного года. При этом может оказаться, что продолжительность нового периода, выраженная в годах, составит величину, представляющую собой отношение двух целых чисел, например 7: 6. Это будет означать, что по прошествии семи лет тело совершит относительно Солнца шесть оборотов, в то время как Земля совершит в точности семь оборотов. По истечении этого периода времени ситуация встречи тел на орбитах должна повториться. При небольшом отличии от точной соизмеримости периодов возможно даже ухудшение ситуации, имевшей место в предыдущем сближении. Например, если в предыдущем сближении тело прошло через точку минимального расстояния между орбитами немного ранее, чем Земля, ввиду чего столкновения тел не произошло, то к моменту очередного сближения тело может несколько задержаться и прийти в роковую точку одновременно с Землей. Как показывают расчеты, для 2004 MN4 в результате сближения в 2029 г. возможен целый спектр неблагоприятных преобразований орбиты, которые ведут либо к непосредственным столкновениям через несколько лет с Землей, либо к новым очень тесным сближениям с нею и новым опасным трансформациям орбиты в будущем.

В ближайшие десятилетия или даже столетия астероид будет являться источником постоянной угрозы для Земли, пока вековые возмущения перигелия и узлов орбиты не уведут его восходящий узел на эклиптике достаточно далеко от орбиты Земли. Правда, эти же возмущения через несколько тысяч лет приведут к опасной близости к орбите Земли его нисходящий узел [Заботин, Медведев, 2008]. На интервалах в десятки тысяч лет движения перицентра и узлов будут периодически приводить орбиту астероида к пересечениям с орбитой Земли. Орбита астероида является, таким образом, динамически неустойчивой. В конечном итоге астероид либо выпадет на Землю, либо в результате тесных сближений с нею большая полуось и эксцентриситет его орбиты будут радикально преобразованы, и астероид выпадет на Солнце (при очень большом эксцентриситете) или получит возможность сближаться с другими большими планетами и эволюционировать под влиянием тесных сближений с ними.

Такова в общих чертах картина движения данного астероида и эволюции его орбиты. В июне 2005 г. астероид 2004 MN4 получил постоянный номер 99942 и вскоре после этого ему было присвоено имя Apophis (Разрушитель) (греческое имя египетского божества Aпеп, которое, согласно легенде, таится во мгле и пытается разрушить Солнце во время его ночных странствий по подземному миру).

7.7.2. Точность знания орбиты Апофиса на современном этапе. Для оценки угрозы Земле со стороны (99942) Апофиса первостепенное значение имеет знание его точной орбиты. Орбита астероида имеет необычайно малое межорбитальное расстояние с орбитой Земли, равное 0,00027 а.е. Это определяет возможность очень тесных сближений астероида с Землей, которые происходят в окрестности 13 апреля, если Земля пересекает линию узлов орбиты Апофиса на эклиптике почти одновременно с астероидом. Ближайшее по времени тесное сближение Апофиса с Землей произойдет 13 апреля 2029 г., когда минимальное расстояние между их центрами будет около 38 000 км (рис. 7.4). Размеры Апофиса (?270 ± 60 м) и особенности его орбиты таковы, что до 2012 г. трудно ожидать его новых наземных наблюдений (см. ниже).

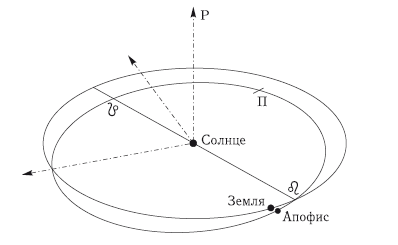
Рис. 7.4. Положения Земли и Апофиса на их орбитах 1 апреля 2029 г.

Радарные наблюдения более информативны и позволяют даже при небольшом их числе существенно повысить точность определения орбиты. Известны, по крайней мере, четыре определения орбиты Апофиса с использованием имеющихся радарных и большей части оптических наблюдений. Все четыре системы параметров орбиты найдены путем взвешенного уравнивания систем условных уравнений и их решения по методу наименьших квадратов. Представляет значительный интерес сравнение найденных параметров орбит и полученных оценок их точности. Как уже было сказано, из-за небольших различий в значениях параметров в начальную эпоху проистекают существенные различия в прогнозе движения Апофиса после 2029 г. и различия в оценке вероятности его столкновения с Землей в 2036 г. и в последующие годы. Ниже дается оценка того, насколько близки найденные решения друг к другу и сколь существенно может отличаться прогноз движения на время после 2029 г. из-за различия моделей движения и неучтенных факторов, влияющих на движение астероида.

Были проведены сравнения систем элементов орбиты и оценки их точности, полученные в Институте прикладной астрономии (ИПА) РАН, Лаборатории реактивного движения (ЛРД НАСА, США), в Пизанском университете (Италия) (NEODyS) и группой сотрудников ЛРД, радиообсерватории Аресибо и Калифорнийского технологического института [Giorgini et al., 2008]. Первые три системы найдены на эпоху 2007, апрель 10,0, четвертая система — на эпоху 2006, сентябрь 1,0. При получении каждой системы было использовано разное число оптических наблюдений. Различалась и процедура назначения весов условным уравнениям. Соответственно различаются и оценки средней ошибки. Тем не менее, первые три системы весьма близки друг к другу, и различие между ними находится в пределах найденных ошибок элементов.

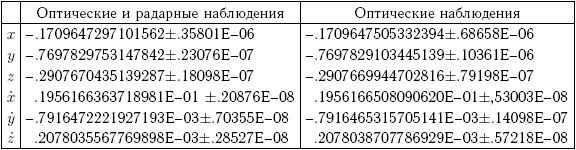
В табл. 7.1 представлены значения координат и компонент скорости Апофиса и их среднеквадратичные погрешности (решение ИПА РАН). Для сравнения рядом указываются данные, соответствующие решению, полученному только по оптическим наблюдением. Очевидно, что включение в решение радарных наблюдений увеличивает его точность в несколько раз.

Таблица 7.1. Координаты и компоненты скорости Апофиса в эпоху JD 2454200,5 (10.04.2007) и их средние ошибки, полученные при использовании оптических и радарных и только оптических наблюдений

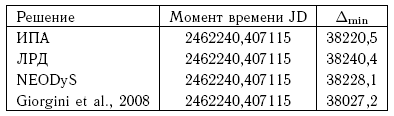
7.7.3. Сближение с Землей в 2029 г. Интересно проследить, какие следствия вытекают из различий между полученными решениями. Эти различия в первую очередь касаются минимального расстояния между Землей и Апофисом, достигаемого 13 апреля 2029 г. Величины этих расстояний в момент времени JD 2462240,407115, близкий к эпохе максимального сближения этих тел в 2029 г., представлены в табл. 7.2.

Следует оговориться, что только в случае решения ИПА эти величины подсчитаны в полном соответствии с моделью, использованной при уточнении орбиты. В решении [Giorgini et al., 2008]) использована так называемая стандартная динамическая модель (учет гравитационных возмущений от больших планет, Земли и Луны, трех малых планет и релятивистских возмущений).

Таблица 7.2. Минимальные расстояния между Землей и Апофисом 13 апреля 2029 г.

В случае решения ИПА добавлен учет светового давления и сжатия Земли и Солнца, а также учет эффекта фазы. Модели движения, использованные в двух других случаях, лишь незначительно отличались от модели, использованной в ИПА. Несмотря на некоторое различие использованных моделей, видно, что все четыре решения дают близкие значения минимального расстояния между Землей и Апофисом.

Следующим этапом рассмотрения сближения является построение эллипса рассеяния в плоскости цели (см. раздел 7.5). Расчеты, выполненные на момент времени JD 2462240,407115, дают ? = 7125 км, ? = 37 550 км, a? = 15,0 км, a? = 351,6 км (рис. 7.5).

Если эллипс рассеяния ограничить только теми точками, которые образованы виртуальными астероидами, берущими начало в области начального эллипсоида рассеяния с осями ±3?Ei, то его большая полуось равна 3a?, а малая — 3?Ei. Эллипс рассеяния, таким образом, весьма вытянут (рис. 7.5). Расстояние от центра эллипса рассеяния до центра Земли столь велико и размеры эллипса столь малы, что ни о каком столкновении в 2029 г. речи быть не может.

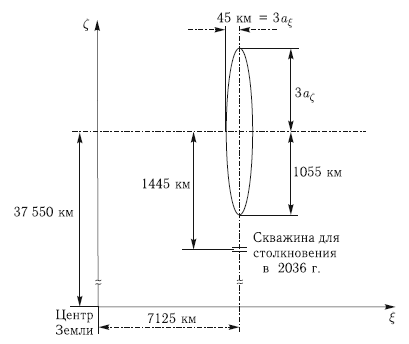
Рис. 7.5. Положение эллипса рассеяния на плоскости цели 13 апреля 2029 г.

7.7.4. Возможность резонансных возвращений в 2036 г. и в последующий период. Различные точки большой полуоси эллипса рассеяния соответствуют различным виртуальным астероидам. Если в номинальном решении варьировать значение среднего движения в пределах от +3?n до величины -3?n, а все остальные элементы оставлять неизменными, то точки пересечения виртуальных астероидов с плоскостью цели пробегают всю большую ось эллипса, начиная с ближайшего к Земле ее конца и заканчивая наиболее удаленным концом (рис. 7.5). Соответствующие виртуальные астероиды пройдут на различных расстояниях от центра Земли и поэтому их орбиты изменятся по-разному.

Особенно значительны по своей величине и возможным последствиям будут изменения большой полуоси. Так, среднее движение астероида, прошедшего через ближайший к Земле конец большой оси эллипса, изменится от 1,11385 до 0,84407 °/сут, а среднее движение астероида, прошедшего через дальний конец большой оси эллипса, изменится от 1,11385 до 0,85429 °/сут. Измененным значениям среднего движения соответствуют периоды обращения, выраженные в годах, P = 1,1677 и P = 1,1537. В силу непрерывности существуют виртуальные астероиды, которые будут иметь периоды обращения, равные любому числу в указанных пределах. В частности, верхний предел близок к отношению 7: 6 ? 1,1667. Виртуальные астероиды с периодами, близкими к 1,1667 года, по истечении семи лет, совершив шесть оборотов вокруг Солнца, опять окажутся вблизи Земли, и минимальное расстояние от Земли для некоторого множества из них может оказаться меньше или равным радиусу Земли, что будет означать столкновение. Более точное представление о реальной ситуации в апреле 2036 г. можно получить, если численным путем проследить движение большого числа виртуальных астероидов, чьи точки пересечения с плоскостью цели в апреле 2029 г. располагаются вдоль большой оси эллипса рассеяния. Получить начальные условия для таких виртуальных астероидов можно путем варьирования среднего движения Апофиса в начальную эпоху в пределах ±3?n (для большей гарантии вариацию можно брать в более широких пределах). Значения минимальных расстояний между Апофисом и Землей в 2036 г., полученные для вариаций среднего движения в пределах от +11 252 10-11 до +11 257 10-11 °/сут, приведены в табл. 7.3.

Таким образом, вариация номинального значения среднего движения примерно в указанных пределах ведет к столкновению Апофиса с Землей в 2036 г. Так как согласно решению ИПА ?n = 2739 10-11 °/сут, то указанные вариации, хотя они и несколько превышают величину 4?n, тем не менее, имеют не исчезающе малую вероятность. Интересно выяснить, в каком месте плоскости цели соответствующие виртуальные астероиды пересекают ее. Очевидно, что точки пересечения располагаются на продолжении большой оси эллипса рассеяния, занимая некоторый его отрезок. Один конец отрезка соответствует величине вариации 4,1082?n, а второй — вариации, равной 4,1100 ?n. На плоскости цели вариация, равная ?n, соответствует величине a? = 351,6 км. Из этого следует, что один конец отрезка находится на расстоянии 4,1082 351,6 = 1444,4 км от центра эллипса, а другой — на расстоянии 4,1100 351,6 = 1445,0 км, т. е. длина отрезка составляет около 600 м (рис. 7.5).

Таблица 7.3. Минимальные расстояния между Апофисом и Землей в 2036 г. при различных вариациях среднего движения астероида (решение ИПА)

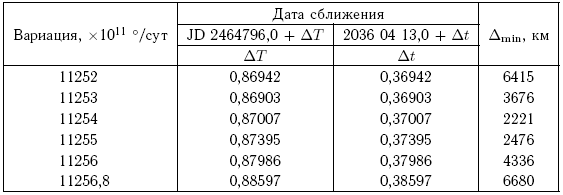
Это так называемая «замочная скважина» (англ. keyhole) на плоскости цели, через которую должен пройти центр Апофиса, чтобы через шесть лет астероид столкнулся с Землей. Вариация других элементов орбиты астероида мало влияет на этот вывод. С учетом их вариации отрезок большой оси превратится в щель на плоскости цели, ограниченную с боков контуром эллипса шириной около 600 м, но результат в принципе останется прежним.

Совершенно аналогично для решения [Giorgini et al., 2008] при указанных в табл. 7.4 значениях вариации среднего движения находим соответствующие им значения ?min (номинальное значение среднего движения равно 1,1128077236422 ± 1733 10-11 °/сут, эпоха JD 2453979,5).

Таблица 7.4. Минимальные расстояния между Апофисом и Землей в 2036 г. при различных вариациях среднего движения астероида (решение [Giorgini et al., 2008])

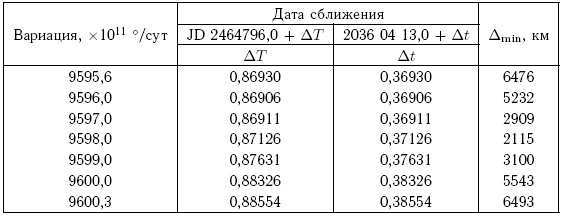
Итак, уже при иных значениях вариации среднего движения решение [Giorgini et al., 2008] также приводит к столкновению, хотя и в чуть более поздний момент времени. В табл. 7.5 сопоставлены расчеты вероятности столкновения Апофиса с Землей в 2036 г., выполненные на основе различных решений.

В таблице для каждого из трех решений последовательно приводятся следующие данные: cреднее движение в исходную эпоху и оценка его ошибки; минимальное расстояние астероида от Земли в апреле 2029 г.; интервал вариаций среднего движения, приводящих к столкновению в апреле 2036 г.; варьированное значение среднего движения в эпоху JD 2454200,5, соответствующее средней по величине вариации; минимальное расстояние от центра Земли в 2036 г.; расстояние от центра Земли до середины «замочной скважины» (скважины для столкновения, или зоны резонансного возврата), ведущей к столкновению в 2036 г.; ширина скважины, выраженная в единицах ошибки среднего движения для данного решения; вероятность столкновения Апофиса с Землей в 2036 г.

Таблица 7.5. Вероятность столкновения Апофиса с Землей согласно различным решениям

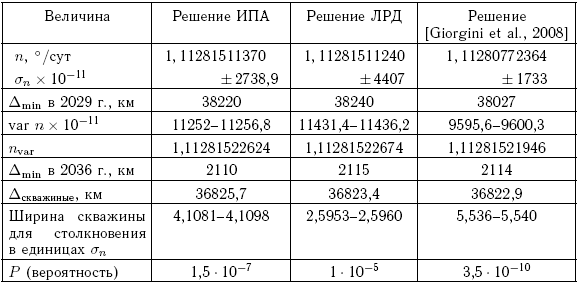
Следует особенно подчеркнуть два момента. Первый момент — это близкие положения «замочных скважин» для всех трех решений: разница их расстояний от Земли находится в пределах 2–3 км.

Второй момент, на который следует обратить внимание, — это очень большой разброс в оценке вероятности столкновения, вытекающей из различных решений. Оценка вероятности столкновения с учетом неполноты наших знаний о величине сил, действующих на астероид, будет рассмотрена в следующем параграфе.

Если виртуальный астероид пройдет мимо «замочной скважины», но близко к ней, то в 2036 г. столкновение будет исключено, но в результате такого тесного сближения с Землей орбита астероида претерпит новые изменения, которые могут привести к опасным сближениям в обозримом будущем. Это весьма неприятная ситуация, так как в результате двух последовательных тесных сближений астероида с Землей точность предсказания его дальнейшего движения резко снижается. Самые, на первый взгляд, малозначительные изменения действующих на астероид сил или потеря точности при интегрировании могут вести к неправильному прогнозу его движения после серии последовательных тесных сближений.

Скважины на плоскости цели 2029 г. отнюдь не единственные в своем роде (см. рис. 10.13 в главе 10). Например, на расстоянии всего в 142 км от центра эллипса рассеяния, по другую сторону от «замочной скважины», ведущей к столкновению в 2036 г., находится скважина для столкновения с Землей в 2051 г. Правда, в данном случае расчет показывает не прямое столкновение, а лишь касательное прохождение астероида мимо Земли на высоте всего в 2000 км. Ширина «замочной скважины», ведущей к касательным прохождениям на высотах, не превышающих 3500 км над поверхностью Земли, составляет 165 м.

7.7.5. Иcследование резонансных возвратов с помощью метода точечных гравитационных сфер. Как уже обсуждалось в этой главе, каждое тесное сближение астероида с планетой сопровождается рассеянием трубки его возможных траекторий и заметной потерей точности прогнозирования движения астероида. Траектории виртуальных астероидов, близкие до прохождения около планеты, претерпевают различные возмущения и расходятся после сближения с ней. С аналогичной трудностью небесные механики сталкивались уже давно при исследовании комет, сближающихся с Юпитером. Она имеет место и для астероида Апофис, а также для других опасных астероидов в случае их тесных сближений с планетами.

После сближения Апофиса с Землей в 2029 г. точность прогнозирования его движения резко падает. Если же для части возможных траекторий после 2029 г. будет иметь место тесное сближение (не соударение!) в 2036 г., то дальнейшее движение по этим траекториям становится практически недетерминированным. Другими словами, современной точности начальных данных недостаточно для исследования методом численного интегрирования возможных соударений в период, последующий за 2036 г., если в этом году будет иметь место тесное сближение астероида с Землей. По мере получения новых наблюдений точность орбиты будет, конечно, расти, однако в ближайшие несколько лет вряд ли удастся достаточно точно предвычислить траектории тесных сближений в 2036 г., чтобы надежно проанализировать все возможные сближения и возможные столкновения в последующие годы.

Интуитивно ясно, что опасными траекториями, на которые может перейти астероид в результате тесного сближения с Землей, являются резонансные траектории невысокого порядка. Например, если после сближения астероид окажется на орбите, которая имеет соизмеримость средних движений 1:1 с Землей, то ровно через год астероид и Земля окажутся в том же месте и возможно их новое тесное сближение или соударение. Из-за расширения трубки возможных траекторий в результате взаимодействия с Землей существует больше возможностей попадания в такие опасные резонансы. Соответствующие области начальных условий называют зонами резонансного возврата. Так, в работе [Chesley, 2005] рассмотрены возможные резонансные возвраты астероида Апофис после сближения в апреле 2029 г. Ко времени написания работы Чизли орбита астероида имела еще сравнительно низкую точность, и в результате рассеяния трубки возможных траекторий после этого сближения астероид мог оказаться на различных резонансных орбитах, указанных на рис. 10.13 в главе 10. Эти орбиты приводили к опасным сближениям Апофиса с Землей в 2034, 2035, 2036, 2037, 2038, 2046 и 2048 гг. Однако по мере увеличения точности орбиты число возможных резонансных возвратов быстро уменьшалось, и уже к августу 2005 г. остался лишь один возможный резонансный возврат в апреле 2036 г. Существенно в этой связи, что в ближайшие несколько лет до 2012 г. точность орбиты астероида Апофис не будет расти в результате поступления новых наблюдений, поскольку в это время наблюдать его с Земли практически невозможно. После появления новых наблюдений и уточнения орбиты Апофиса в 2012–2013 гг. совершенно аналогично уменьшится число возможных траекторий с опасными сближениями в период после 2036 г., которые детально обсуждаются в работе [Соколов и др., 2008].

В первом приближении резонансные возвраты можно исследовать, используя прием, называемый методом точечных гравитационных сфер (ТГС). Для нескольких последовательных сближений с планетой этот метод позволяет с умеренной трудоемкостью получить картину возможных преобразований орбит. При этом, если сближения достаточно тесные и относительная скорость достаточно велика, метод дает приемлемую точность результатов. Точность определяется из сравнения с результатами численного интегрирования неупрощенных уравнений движения. Метод ТГС позволяет в ряде важных случаев рассматривать вместо сложной задачи трех тел последовательность простых задач двух тел. Этот прием в различных модификациях часто применяется в небесной механике и механике космического полета, в частности для проектирования траекторий космических аппаратов с несколькими гравитационными маневрами. Некоторые подробности, а также литературные ссылки можно найти, например, в работах [Соколов и др., 2008; Елькин и др., 2003].

В методе ТГС исследуемая траектория аппроксимируется последовательностью кеплеровых гелиоцентрических орбит соударения с планетами. При «соударении» происходит мгновенное преобразование скорости — поворот вектора планетоцентрической скорости на угол между асимптотами планетоцентрической гиперболы. Модуль планетоцентрической скорости остается при этом постоянным. Элементы кеплеровой орбиты преобразуются в этом случае по формулам классической задачи двух тел. Как известно, по координатам и скоростям в данный момент времени элементы орбиты определяются однозначно. Угол поворота вектора планетоцентрической скорости зависит от прицельного расстояния и в рамках рассматриваемой аппроксимации (сжатия гравитационной сферы в точку, обнуления прицельного расстояния) не определен, т. е. может быть произвольным в некоторых пределах.

Для исследования траекторий, содержащих опасные сближения и соударения астероида Апофис с Землей сразу после возможного тесного сближения в 2036 г., в работе [Соколов и др., 2008] используются следующие методы. В предположении, что движение в промежутке между 2029 и 2036 гг. происходит по резонансной орбите соударения с соизмеримостью средних движений 6:7, методом ТГС строится множество возможных резонансных кеплеровых орбит соударения после тесного сближения в 2036 г. Затем с использованием численного интегрирования уравнений движения с учетом всех возмущений ищутся траектории тесных сближений и соударений с Землей, близкие к построенным кеплеровым резонансным орбитам соударения. Для преодоления основной трудности — потери точности из-за тесных сближений, область допустимых начальных данных можно транспортировать вдоль траекторий в 2035 г., в результате чего ее размеры увеличиваются на несколько порядков. После этого численное нахождение начальных данных, соответствующих опасным траекториям, не представляет принципиальных трудностей. Полученные методом ТГС приближенные значения минимальных геоцентрических расстояний используются при нахождении интересующих нас опасных сближений в качестве первых приближений, начальные данные для численного интегрирования берутся из новой области в 2035 г. Аналогичный подход использовал Ж. Ласкар при исследовании динамического хаоса в Солнечной системе и поиске «уходящих» из нее траекторий Меркурия.

В результате с использованием методов, указанных в работе [Соколов и др., 2008], были построены порождающие эллиптические резонансные траектории соударений в 2037–2052 гг. (95 траекторий). Некоторые из них не могут быть реализованы, так как проходят в 2036 г. на геоцентрическом расстоянии менее радиуса Земли, однако большинство соответствует реальным траекториям. Подробнее были рассмотрены порождающие траектории с соударениями до 2041 г. включительно: численно получены траектории, содержащие соударения Апофиса с Землей в 2040 и 2041 гг. (резонансы 3:4 и 6:5 после 2036 г.), а также тесные сближения в 2037, 2038 и 2039 гг. Численное интегрирование подтвердило корректность использования метода ТГС для построения приближенных решений в случае Апофиса. Для численного интегрирования использовался интегратор Эверхарта. Движение планет и Луны описывалось известными динамическими моделями DE403 и DE405. Минимальные геоцентрические расстояния после 2036 г., полученные по DE403 и DE405, различаются незначительно, разница обычно менее 1 км. Области начальных значений координат в 2035 г., соответствующие указанным соударениям в 2040 и 2041 гг., имеют размеры порядка сотен и десятков метров соответственно. Отметим, что размеры областей начальных данных, соответствующие соударениям, по DE403 и DE405 практически совпадают, в то время как сами эти области отстоят друг от друга на десятки километров.

Представляет также интерес история сближений Земли и Апофиса. Проведенное численное интегрирование от 2006 г. до 1700 г. показало отсутствие тесных сближений на этом интервале. Все сближения происходят 12–14 апреля. Самое тесное сближение имело место в 1819 г. до расстояния 0,84 млн км. Остальные шесть сближений происходили до расстояний 3–4 млн км.

На примере астероида Апофис хорошо видны некоторые важные аспекты проблемы астероидно-кометной опасности, на которые раньше не обращали должного внимания. Так, соударению астероида с планетой могут предшествовать сближения с ней, хотя бы потому, что сближения на умеренные расстояния более вероятны, чем соударения. Этот вопрос обсуждается, в частности, в работе [Елькин, Соколов, 1995]. Отмеченное обстоятельство позволяет заблаговременно обнаружить потенциально опасный объект. С другой стороны, рассеяние возможных траекторий при тесных сближениях ведет к потере точности, затрудняет прогнозирование движения и требует применения специальных методов. Среди возможных движений астероида после тесных сближений появляются опасные траектории, имеющие резонансные возвраты к Земле. Соответствующие «замочные скважины», или зоны резонансного возврата, имеют очень малые размеры и, следовательно, мала вероятность столкновения с Землей. Точное положение «скважин» зависит от величины возмущающих сил: малые недостаточно известные эффекты могут изменить место «скважин» в пространстве начальных данных. Точное определение их положения является сложной актуальной задачей. В то же время само наличие «скважин» и их размеры мало зависят от возмущений. Следует отметить сложную структуру соответствующего множества, аналогичную фрактальной. Небольшое искусственное изменение траектории астероида (удар по нему и т. п.) с целью предотвратить соударение в апреле 2036 г. не гарантирует отсутствия соударений в последующие несколько лет. Отклонив траекторию, можно попасть в близлежащую «замочную скважину», ведущую к соударению. Недостаточная точность знания орбиты Апофиса не позволяет пока исключить возможность попадания в эти зоны резонансного возврата. Поэтому наряду с совершенствованием методов прогнозирования движения астероидов особую ценность имели бы наблюдения АСЗ из космоса, а также использование для уточнения орбиты Апофиса сигналов радиопередатчика, доставленного на орбиту искусственного спутника этого астероида.

7.7.6. Влияние эффекта Ярковского на движение Апофиса. Во всех рассмотренных случаях модель движения Апофиса не включала влияние эффекта Ярковского (см. раздел 3.6). Он вызывается неравномерным нагревом тела солнечными лучами в результате осевого вращения тела и его движения по орбите. Эффект Ярковского зависит от положения оси вращения, орбиты и массы тела, от теплопроводности его поверхностных слоев. Поскольку большинство этих параметров неизвестны, явным образом учесть эффект невозможно. Однако неявным образом этот эффект частично учитывается в результате подгонки элементов орбиты, прежде всего большой полуоси, к наблюдениям, которые, естественно, отражают влияние эффекта, если он достаточно велик. Тем не менее, значительная часть эффекта остается неучтенной, что может вызвать заметные ошибки при прогнозировании движения тела на основе найденной орбиты. В работе [Giorgini et al., 2008] выполнена оценка максимального смещения Апофиса по орбите за период от эпохи оскуляции (2006 г.) до 2029 г. под действием не учитываемой части эффекта. При предполагаемой массе в зависимости от направления вращения и гипотетически заданной теплопроводности поверхностных слоев максимальное смещение вдоль орбиты может составить к 2029 г. от –720 км до +780 км. Эти значения находятся в качественном согласии с оценками влияния эффекта Ярковского на движение ряда АСЗ, найденными Ю. А. Чернетенко иным путем по сравнению с работой [Giorgini et al., 2008].

В работе [Чернетенко, 2007] учет эффекта Ярковского в движении астероидов производился без каких-либо предположений о физических характеристиках этих тел. Предполагалось лишь, что зависимость этого эффекта от гелиоцентрического расстояния r имеет вид 1/r2, а его величина характеризуется в общем случае тремя составляющими ускорения: радиальной, трансверсальной и нормальной, которые определяются из наблюдений (радарных и оптических) совместно с параметрами орбиты. При этом для астероида (6489) Голевка включение в число определяемых по наблюдениям запаздывания параметров трансверсальной составляющей A2 позволило уменьшить ошибку единицы веса с 2,3 мкс до 0,5 мкс. Величина A2 оказалась равной (-2,00 ± 0,14) 10-14 а.е./сут2.

При оценке влияния эффекта Ярковского на движение астероида Апофис было принято, что зависимость ускорения от гелиоцентрического расстояния имеет вид 1/r2, а для A2 принимались некоторые возможные значения (+2, –2, +6, –6) 10-14 а.е./сут2. Значения минимального расстояния от Апофиса до Земли и смещения астероида вдоль орбиты на 13 апреля 2029 г., полученные в результате уточнения параметров движения и последующего интегрирования, приведены в табл. 7.6.

Таблица 7.6. Влияние принятых значений ускорения, вызываемого эффектом Ярковского, на величину минимального расстояния от Апофиса до Земли и смещение астероида вдоль орбиты на 13 апреля 2029 г.

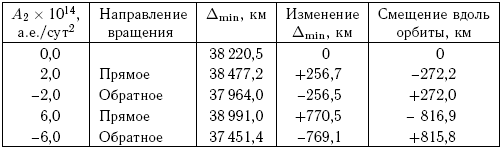
Изменения смещения вдоль орбиты при A2 = (+6,-6) 10-14 а.е./сут2 близки к оценкам, полученным в работе [Giorgini et al., 2008]. Конечно, подобные расчеты имеют только качественный характер, поскольку реальное значение A2 из имеющихся наблюдений найти невозможно. Но метод может быть использован в будущем, если будет получено необходимое число достаточно точных наблюдений.

Оценим теперь, как влияет эффект Ярковского на положение эллипса рассеяния на плоскости цели и на вероятность столкновения Апофиса с Землей в 2036 г. Будем исходить из предположения, что величина A2 для астероида равна -2 10-14 а.е./сут2, что приводит к сокращению его полуоси и к увеличению среднего движения. В результате к апрелю 2029 г. астероид сместится вдоль орбиты на величину +272 км (табл. 7.6). Таким образом, астероид, соответствующий номинальному решению, найденному с учетом дополнительного ускорения, пересечет плоскость цели несколько раньше, и его минимальное расстояние от Земли составит, как показано в табл. 7.6, 37 964 км по сравнению с расстоянием в 38 220,5 км, на котором астероид должен проследовать мимо Земли в 2029 г. согласно решению, полученному ИПА.

7.7.7. Перспективы уточнения орбиты Апофиса. Для планирования возможного изменения орбиты Апофиса в случае, если это изменение будет вести к неизбежному или весьма вероятному столкновению, важно иметь представление о том, каковы перспективы проведения дальнейших астрометрических и физических наблюдений данного астероида и какого уточнения модели движения астероида можно ожидать в предстоящий период. При рассмотрении данного вопроса важно иметь в виду, что активные действия по изменению орбиты Апофиса должны быть предприняты до 2029 г. Величина корректирующего одиночного импульса, прикладываемого к астероиду до апреля 2029 г., чтобы избегнуть столкновения в 2036 г., примерно на три порядка меньше необходимого импульса после сближения в 2029 г. [Ивашкин, Стихно, 2008]. Причина такого различия вполне понятна. В случае, если коррекция выполняется до 2029 г., необходимо лишь несколько изменить минимальное геоцентрическое расстояние астероида (изменить орбиту так, чтобы ее пересечение с плоскостью цели произошло вне ближайшей окрестности «замочной скважины» размером около 600 м). Остальную работу по изменению траектории выполнит гравитационное поле Земли. После 2029 г. гелиоцентрическую орбиту астероида придется смещать уже на величину порядка нескольких радиусов Земли.

Размеры астероида и особенности его орбиты таковы, что благоприятные условия для его наблюдения складываются лишь в определенные весьма непродолжительные периоды времени. На рисунках 7.6–7.8 показаны элонгация астероида Апофис от Солнца, его звездная величина и расстояние от Земли в период 2006–2024 гг. На протяжении 2009–2011 гг. видимая звездная величина астероида будет оставаться в пределах 19,5m–22,1m. Но относительно большой блеск имеет место при малых элонгациях от Солнца. Сомнительно, что при звездной величине, превышающей 21m, астероид можно будет наблюдать в элонгациях, меньших 50°. Таким образом, ближайшее «окно» для оптических наблюдений откроется не ранее декабря 2011 г., когда элонгация превысит 50°, а звездная величина будет меньше 21m.

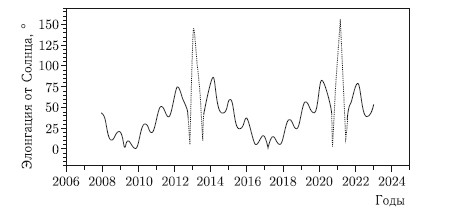
Рис. 7.6. Элонгация астероида Апофис от Солнца

Возможности проведения новых радиолокационных наблюдений Апофиса также очень ограничены. Для наиболее крупного 300-м радиолокатора в Аресибо (Пуэрто-Рико, США) предельно возможное расстояние приема отраженного от астероида сигнала (при заданных размерах астероида и значении радиоальбедо его поверхности) составляет 0,31 а.е. Для 70-м локатора в Голдстоуне (США) расстояние приема составляет всего 0,14 а.е.

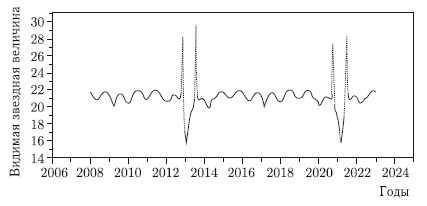
Рис. 7.7. Видимая звездная величина астероида Апофис

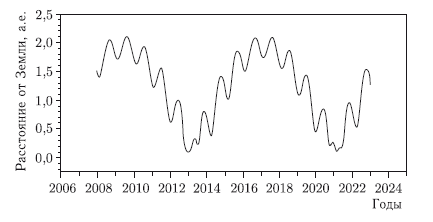
Рис. 7.8. Расстояние от астероида Апофис до Земли

Примерно такие же возможности имеются у радиолокатора в Евпатории и модернизируемого радиотелескопа в Уссурийске. Таким образом, «окна» для радиолокационных наблюдений будут открыты только в конце 2012 г. — первой половине 2013 г., в октябре 2020 г. и феврале — августе 2021 г.

В работе [Chesley, 2005] предпринята попытка оценить, насколько точно может быть определена орбита Апофиса из возможных оптических и радиолокационных наблюдений, при условии, что из них будет получена не только астрометрическая информация о положениях Апофиса, но и найдено положение оси и направление вращения астероида. Как отмечалось ранее, две последние величины важны для оценки влияния эффекта Ярковского на движение астероида. В работе предполагается, что в периоды, наиболее благоприятные для наблюдений, каждую вторую ночь будет получено одно астрометрическое наблюдение со средней ошибкой в 0,2?, а в периоды, когда наблюдения будут менее доступны, но все еще возможны для крупных телескопов, одно наблюдение с той же ошибкой будет получено в течение каждой лунации. Далее предполагается, что в периоды 14–20 февраля и 6–10 июля 2013 г., а затем в периоды 9–12 октября 2020 г. и 16–20 марта 2021 г. с помощью радиолокатора в Аресибо будет выполнено в сумме 23 измерения расстояния до астероида с различной точностью в зависимости от расстояния. С учетом уже имеющихся наблюдений и предположительно осуществленных к исходу того или иного интервала можно оценить, с какой точностью определяется большая полуось эллипса рассеяния на плоскости цели в 2029 г. по всем имеющимся на рассматриваемый момент наблюдениям. Из вычислений Чизли следует, что к началу 2014 г. большая полуось эллипса рассеяния сократится примерно до 30 км, а к началу 2022 г. — до величины, несколько превышающей 10 км, если радарные наблюдения осуществлены не будут, и до 1 км, если они будут выполнены. Кроме того, в работе Чизли моделируется уточнение эллипса рассеяния с учетом годичного приема радиосигналов с эквивалентной точностью ±2 м от передатчика, доставленного на Апофис в 2019 г. С учетом радионаблюдений точность определения большой полуоси эллипса рассеяния повысится до 100 м.

В работе [Giorgini et al., 2008] эта проблема также обсуждается, но с применением иных подходов. Впрочем, результаты в целом оказываются сопоставимыми.

Можно поставить вопрос: какова вероятность того, что с учетом всех факторов столкновение с Апофисом в 2036 г. произойдет, и как вероятность столкновения будет эволюционировать с течением времени? Можно попробовать найти ответ на этот вопрос, если еще раз обратиться к рис. 7.5. Мы уже видели, что «замочная скважина» для столкновения в 2036 г. располагается на расстоянии 1444,7 км = 4,11?? от центра эллипса, что определяет малую вероятность столкновения. Но при этом не был принят во внимание эффект Ярковского. Он способен сдвинуть центр эллипса, а вместе с ним и весь эллипс рассеяния вдоль большой оси в ту или иную сторону. Направление смещения и его величина зависят от положения оси вращения астероида. Если наклон оси вращения к плоскости орбиты астероида меньше 90° (прямое вращение), то, как нетрудно видеть, реактивный эффект покидающих тело тепловых фотонов имеет составляющую, направленную по вектору орбитальной скорости тела (рис. 7.9).

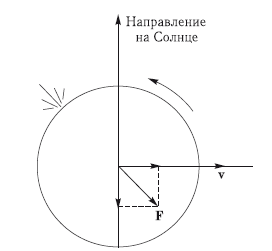
Рис. 7.9. Эффект Ярковского в случае прямого вращения астероида; F — вектор реактивного ускорения, v — орбитальная скорость астероида

Это приводит к увеличению большой полуоси орбиты астероида и уменьшению его среднего движения. Астероид будет двигаться по орбите с некоторым отставанием во времени и догонит плоскость цели 13 апреля 2029 г., несколько позже по сравнению с невозмущенным случаем. Из этого следует, что координата ? центра эллипса окажется больше и астероид пройдет мимо Земли на несколько большем расстоянии от ее центра и от «замочной скважины» (положение последней в возмущенном случае останется практически тем же). В случае обратного осевого вращения астероида все будет обстоять с точностью до наоборот. Астероид пересечет плоскость цели в более ранний момент времени по сравнению с невозмущенным случаем, и весь эллипс как целое сместится в сторону меньших геоцентрических расстояний. По расчету [Giorgini et al., 2008] эффект Ярковского может привести к смещению астероида вдоль орбиты на величину от 325 км до 740 км в зависимости от принятых значений радиуса, плотности вещества и коэффициента теплопроводности. Можно рассчитать, что значение координаты ? при этих смещениях вдоль орбиты изменится на величины того же порядка. При прямом направлении вращения это означает, что расстояние от центра эллипса до «замочной скважины» возрастет на указанные величины и что столкновение практически невозможно (вероятность столкновения меньше 10-7). При обратном направлении вращения эффект Ярковского способен сдвинуть эллипс рассеяния так, что «замочная скважина» окажется в пределах 3a?. Вероятность столкновения в этом случае остается малой, но заметно отличной от нуля.

Данный текст является ознакомительным фрагментом.