10.4. Эффективность непрерывного воздействия на орбиту астероида

10.4. Эффективность непрерывного воздействия на орбиту астероида

Сначала рассмотрим результат длительного воздействия постоянной тяги dg_W, приложенной по оси W (рис. 10.4).

Можно видеть, что результатом приложения тяги вдоль оси W является поворот плоскости орбиты относительно начальной точки приложения непрерывного воздействия. Заметим, что время приложения тяги принималось равным периоду обращения небесного тела.

Решение линеаризованных уравнений имеет вид:

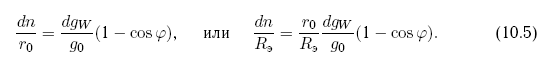
Здесь g₀ — ускорение астероида, вызванное притяжением Солнца: g₀ = µ_c/r₀²,

где µ_c — гравитационный параметр Солнца, а r₀ — радиус орбиты астероида. Величина dg_W представляет собой ускорение тела массой M, создаваемое тягой F. Например, по имеющимся оценкам, масса Апофиса составляет M = 4,6 10¹⁰ кг. Схема изменения орбиты под воздействием тяги dg_W показана на рис. 10.4.

Ясно, что результат изменения текущих координат тела, как и ранее, оказывается чисто периодическим. Максимальный увод будет иметь место через половину витка орбиты, а его величина составит

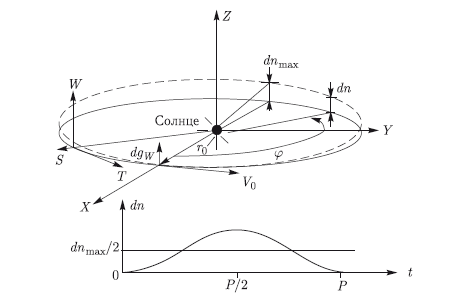
^{Рис. 10.4. Результат длительного воздействия постоянной тяги dg_W, приложенной по оси W}

Обратимся к двум выбранным ранее примерам. В первом случае увода на расстояние, равное диаметру Земли, положив dn_max/R_э = 2, получим, что требуемое значение ускорения dg_W равно: dg_W /g₀ = (R_э/r₀) = 4,25 10^-5. Например, для Апофиса необходимая тяга составит? 11,5 кН (килоньютон). Следовательно, такая тяга, приложенная к Апофису в течение полугода, даст изменение текущих координат на диаметр Земли. Во втором случае (увод из зоны резонансного возврата) тяга, прилагаемая также в течение полугода, оказывается в 1000 раз меньше, т. е. составит всего лишь около 11,5 Н.

Перейдем к случаю приложения тяги dg_S, длительно действующей по оси S. Это воздействие суммируется с ускорением, создаваемым Солнцем, и, следовательно, изменяет период обращения астероида. При постоянной тяге получаем новую орбиту (рис. 10.5), лежащую в той же плоскости.

Следовательно, изменения координат относительно старых значений описываются формулами

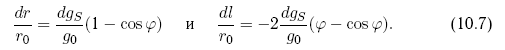
По оси T (вдоль орбиты) появился вековой уход астероида, линейно нарастающий со временем, суммирующийся с периодической составляющей. Величина этого ухода за один виток будет равна dl/r₀ =-4?(dg_S/g₀). Таким образом, получим удобные выражения для векового ухода за N_в витков и требующегося для этого ускорения:

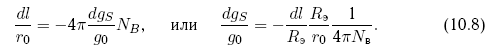
Можно видеть, что приложение длительной по времени тяги по радиус-вектору оказывается более эффективным, чем по нормали. Кроме того, оно тем эффективнее, чем продолжительнее действие тяги. Действительно, в предыдущем случае увод на расстояние dl/R_э = 2 требовал тяги (dg_W /g₀) = = (R_э/r₀), длящейся полвитка. Теперь же величина тяги dg_S, прилагаемой в течение той же половины витка и создающей увод dl/R_э = 2, оказывается равной (dg_S/g₀) = (R_э/r₀)(1/?).

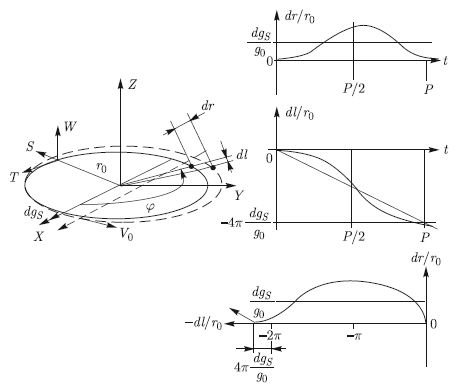
^{Рис. 10.5. Результат длительного воздействия постоянной тяги dg_S, приложенной по оси S}

Таким образом, для того же ограниченного времени действия тяги и заданного значения увода изменение направления прилагаемой силы с трансверсального на радиальное дает выигрыш примерно в 3 раза. Увеличив время непрерывного действия до полного витка орбиты, можно при том же значении увода снизить значение тяги вдвое. Дальнейшее увеличение времени непрерывного воздействия тяги позволит еще больше уменьшить ее необходимое значение. Характер увода астероида от начальной точки в относительных координатах показан на рис. 10.5 справа внизу. Это колебания с постоянной амплитудой по радиус-вектору, но приблизительно линейно нарастающие и отстающие вдоль орбиты.

В заключение данного раздела рассмотрим случай непрерывно действующей тяги dg_T по оси T, которая оказывается наиболее результативной. Вектор тяги, направленный вдоль орбиты, создает ускорение, вызывающее изменение периода обращения угрожающего тела, нарастающее со временем. Теперь орбита будет представлять собой разворачивающуюся спираль (рис. 10.6).

Следовательно, появится линейный вековой уход астероида по координате S и квадратично нарастающий — по координате Т. Соответствующий анализ дает соотношения:

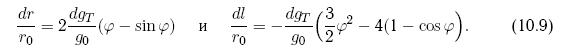
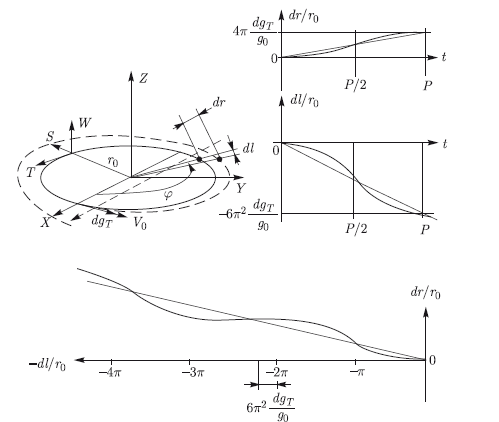
^{Рис. 10.6. Результат длительного воздействия постоянной тяги dg_T, приложенной по оси T}

Из этих соотношений получим величины вековых уходов за N_в витков:

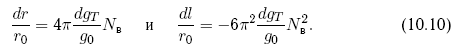
Таким образом, наиболее существенен и эффективен увод по оси T. Увод нарастает линейно по радиус-вектору и квадратично — по нормали. В результате получаем прогрессивно нарастающее относительное отставание от первоначального положения угрожающего астероида. Применяя прежнюю удобную нормировку, получим выражения для увода вдоль орбиты и требуемого ускорения:

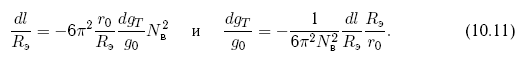
Обращаясь к примерам, получим, что для астероида Апофис в первом случае потребуется в течение одного витка создавать ускорение, равное dg_T = 30 10^-6 м/c², и тягу, составляющую ? 10 кгc. Для второго случая потребная тяга при тех же остальных условиях окажется равной ? 5 гс. Последний пример является иллюстрацией возможности увода с помощью весьма малых реактивных сил, например способом гравитационной буксировки.

Данный текст является ознакомительным фрагментом.