22. Сущности из балка

22. Сущности из балка

Двумерная брана и трехмерный балк

В 1844 году Эдвин Эбботт написал сатирический роман под названием «Флатландия». Хоть сатира на викторианскую культуру в этом романе и кажется старомодной, а отношение к женщинам – возмутительным, само место действия книги имеет прямое отношение к «Интерстеллар», и я очень ее вам рекомендую.

Рис. 22.1. Обложка первого издания «Флатландии»

Роман повествует о приключениях сущности, имеющей форму квадрата и живущей в двумерной вселенной – Флатландии. Квадрат посещает одномерную вселенную, называемую Лайнландией, нульмерную вселенную – Пойнтландию, и, что производит на него особо сильное впечатление, трехмерную вселенную – Спейсландию[67]. Кроме того, когда Квадрат живет во Флатландии, его посещает сферическая сущность из Спейсландии.

При нашей первой встрече с Кристофером Ноланом мы с радостью обнаружили, что оба знаем и любим роман Эбботта.

Представьте что вы, подобно Квадрату в романе Эбботта, – двумерная сущность, живущая в двумерной вселенной, напоминающей Флатландию. Ваша вселенная может быть поверхностью стола, или листком бумаги, или резиновой мембраной. В традициях современной физики я буду называть ее двумерной браной.

Получив хорошее образование, вы предполагаете существование трехмерного балка, в котором находится ваша брана, но вы в этом не уверены. Представьте свою радость, когда однажды вас посетит сфера из трехмерного балка. «Сущность из балка» – так вы могли бы ее называть.

Сначала вы не понимаете, что это сущность из балка, но понаблюдав за ней и хорошенько подумав, не находите иного объяснения. А наблюдаете вы следующее: внезапно, без предупреждения и непонятно откуда, на вашей бране возникает синее пятно (рис. 22.2 сверху слева). Пятно разрастается, превращаясь в синюю окружность, диаметр которой увеличивается до максимального (рис. 22.2 посередине слева), а затем снова сжимается в точку (рис. 22.2 снизу слева) и, наконец, полностью исчезает.

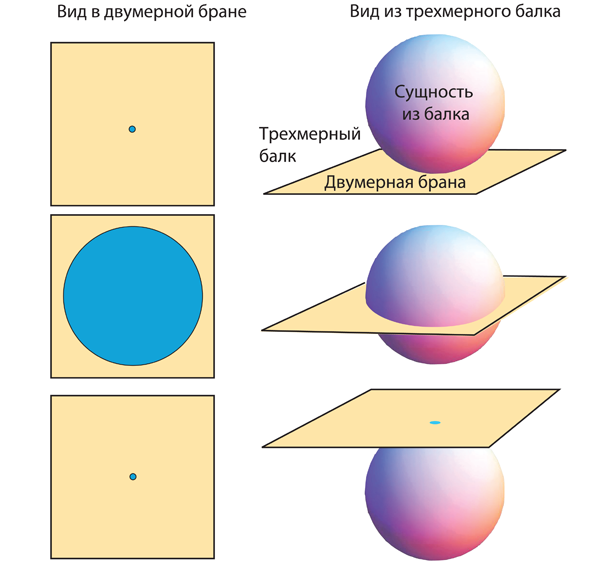
Рис. 22.2. Трехмерная сфера проходит через двумерную брану

Вы верите в принцип сохранения вещества: никакой объект не может возникнуть из пустоты, но этот – появился. Единственное найденное вами объяснение показано на правой половине рис. 22.2. Трехмерная сущность из балка – сфера – проходит через вашу брану. По мере этого вы наблюдаете в своей бране ее изменяющееся двумерное сечение. Сначала это сечение около «южного полюса» сферы, точка (рис. 22.2 сверху справа). Дойдя до экваториальной плоскости, оно расширяется до окружности максимального диаметра (рис. 22.2 посередине справа). И, наконец, у «северного полюса» оно опять сжимается в точку, после чего исчезает (рис. 22.2 снизу справа).

Представьте, что бы произошло, если бы человек (трехмерная сущность), живущий в трехмерном балке, прошел сквозь вашу двумерную брану. Что бы вы увидели?