11. Плосконапряженное состояние материалов

В сопротивлении материалов чаще всего встречаются задачи, когда напряжение действует в двух направлениях, т. е. является плоским. Рассмотрим такое состояние.

Возьмем произвольную точку тела и рассмотрим элементарный параллелепипед с длинами сторон dx, dy, dz в ее окрестности. Рассечем этот параллелепипед плоскостью, перпендикулярной плоскости zy (Рис. 5.1).

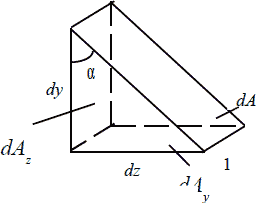
Рис. 5.1

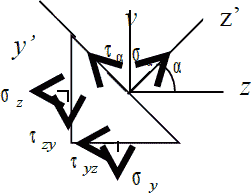
Рис. 5.2

На Рис. 5.2 изображены напряжения на поверхности полученной призмы. Из условий равновесия треугольной призмы через проекции сил, действующих на грани, на оси y’ и z’, можно найти напряжения на наклонной грани призмы.

s_?dA – ?_zdA_zcos? – ?_ydA_ysin? – ?_zydA_zsin? – ?_yzdA_ycos? = 0

?_?dA+ ?_zdA_zsin? – ?_ydA_ycos? – ?_zydA_zcos? + ?_yzdA_ysin? = 0

Учитывая, что dA_z = 1dy = dAcos?, dA_y = 1dz = dAsin?, записанные отношения в результате тригонометрических преобразований примут вид:

?_? = ?_zcos²? + ?_ysin²? + ?_zy sin2?

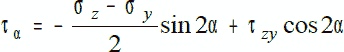
Если совместить оси координат z, y c направлениями главных напряжений, то соотношения примут вид:

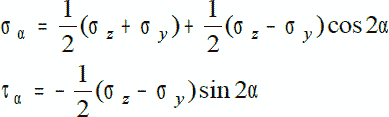
Из последнего уравнения следует, что при ? = 45° касательные выражения принимают свои экстремальные значения в точке.

?_max = ?(?_z – ?_y)

Частный случай плоского напряженного состояния: при ?_x = ?_y ?_? =0, на всех проведенных через точку площадках касательные напряжения равны нулю, т. е. все площадки – главные с нормальными напряжениями ?_? = ?_y = ?_z = ?. Примером такого состояния может служить стенка воздушного шара, находящаяся под давлением.

При ?_x = – ?_y = ? на грани элемента действуют численно равные сжимающие и растягивающие напряжения. Экстремальные касательные напряжения равны главным, а нормальные напряжения равны нулю. Такой частный случай носит название чистого сдвига.