2.9. Кубик Рубика и гравитация

2.9.1. Гравитация – это взаимообмен квантами энергии

Равновесная система. Момент количества движения равен нулю. Возьмем для примера крутильные весы Кавендиша. Шары в крутильных весах расположены на расстоянии ? дуги круга, описываемого плечом коромысла. Можно утверждать, что в данный момент между шарами идет постоянный обмен квантами (импульсами) гравитации, иначе – присутствует взаимное притяжение. Уловить это слабое взаимодействие ни визуально, ни какими приборами невозможно по причине того, что импульс одного фотона имеет очень малую величину. Несмотря на огромное количество перебрасываемых фотонов, статистически они уравновешивают друг друга. Получается своеобразный круговорот квантовой энергии в природе.

Ситуацию можно сравнить с беспрерывным течением жидкости в замкнутом круговом трубопроводе. Если заставить жидкость течь с помощью маломощного насоса, мы не сможем визуально обнаружить течения, так как количество жидкости в каждой единице объема остается постоянным. Чтобы обнаружить течение, необходимо опустить на ее поверхность поплавок.

В крутильных весах, чтобы обнаружить притяжение (переброску квантов-импульсов), необходимо сдвинуть шары на близкое расстояние до появления реакции закручивания подвеса коромысла. В данном случае в роли поплавка выступает закрученный на некоторый угол подвес. При этом общий момент количества движения (масса m на скорость v) остается равным нулю.

?m·v=0

Е₁=Е₂

где Е₁ – это поступившая энергия, Е₂ – энергия данного тела (вещества).

Поскольку в моей лаборатории нет крутильных весов и других более точных приборов, то зайдем в любой технический вуз и заглянем в лабораторию физики. Там, в перерыве между лабораторными занятиями, сидит скучающий лаборант и крутит кубик Рубика, пытаясь собрать его по цветовым граням.

Изрядно помучившись, но так и не достигнув нужного результата, лаборант в сердцах бросает кубик в урну, но промахивается и попадает в сосуд Дьюара с жидким гелием (рис. 2.11).

Для наглядности кубик расположим во фронтальной плоскости, где будем видеть только одну грань.

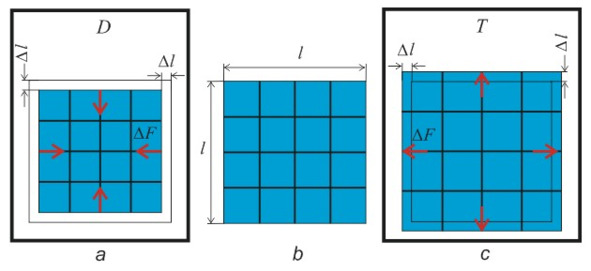
Рис. 2.11. Кубик Рубика находится: a) в сосуде Дьюара; b) на воздухе; c) в тигле.

1. Можно предугадать поведение кубика при температуре окружающей среды – 269^о по Цельсию. Кубик сожмется по всем трем осям (рис. 2.11, а). Его линейные размеры равномерно уменьшатся на величину ?l. В этом случае можно сказать следующим образом: притяжение граней кубика со стороны жидкого гелия стало меньше, чем притяжение при комнатной температуре. Сила притяжения со стороны среды ослабла на величину ?F, и кубик сжался, он втянулся сам в себя.

– ?F=F_He—F

где F_He – сила притяжения жидкого гелия, F – сила притяжения в кубике при комнатной температуре.

2. Жалко игрушку. Лаборант берет щипцы, вытаскивает кубик из сосуда Дьюара, окруженный морозными парами газа. В это время в лабораторию заходит декан и, видя, чем занимается лаборант, вызывает его в свой кабинет, «на ковер».

Далее над кубиком будем издеваться мы. Видим, что кубик «отдышался», принял прежние размеры.

3. Опустим данный кубик в тигель с расплавленным свинцом (t плавления Pb=327^о С) (рис. 2.11, с). Кубик изготовлен из тугоплавкого материала, а на его грани нанесена негорючая краска. Cнова сравним его с эталоном и отметим, что кубик расширился, его линейные размеры по осям увеличились на величину ?l. Данный эксперимент можно описать следующим образом: притяжение граней кубика со стороны расплавленного свинца стало сильнее, чем притяжение при комнатной температуре. Кубик расширился за счет приращения гравитационной силы со стороны свинца на величину ?F.

?F=F_Pb—F

F_Pb – сила притяжения в расплавленном свинце.

3. Вытащим кубик из расплавленного свинца и дадим ему снова «отдышаться» на лабораторном столе для восстановления первоначальных размеров.

Но на этом мучения кубика не заканчиваются. Проведем еще несколько интересных опытов с данной игрушкой, но для этого нам необходимо абстрагироваться и перейти от реального образа к виртуальному. Мысленно представим стенки сосуда Дьюара и тигля аморфными, через которые будем вставлять наш кубик (рис. 2.12).

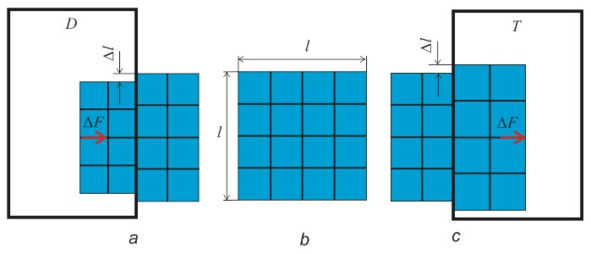
Рис. 2. 12. Кубик Рубика находится: a) наполовину в сосуде Дьюара; b) на воздухе; c) наполовину в тигле.

5. Через боковую стенку Дьюара вставим кубик только наполовину (рис. 2.12, а) и проследим за изменением его размеров. Из рисунка наглядно видно, что левая часть кубика сжалась, а правая часть не изменилась. Левая половина кубика, за счет уменьшения силы притяжения на величину ?F со стороны жидкого гелия, получила смещение вправо. Поскольку обе половины – это две части целого, а одна получила смещение по определенному вектору, то суммарный вектор притяжения будет направлен в ту же сторону, в сторону источника теплоты, в данном случае – смещение вправо.

6. Повторим опыт, но теперь вставим половину кубика в тигель с расплавленным свинцом (рис. 2.12, с). Левая половина кубика осталась неизменной, а правая половина расширилась. Со стороны расплава свинца приложилась дополнительная сила притяжения ?F, и половину кубика растянуло. Кубик в целом получил смещение по результирующему вектору в сторону тигля.

7. Для окончательного вывода проделаем еще два опыта, которые проведем на космической станции, с целью исключения земного тяготения. В невесомости и без трения кубик, помещенный наполовину в сосуд Дьюара, под действием импульсов гравитационного смещения покинет данный сосуд. Кубик, помещенный наполовину в тигель, наоборот, полностью переместится в него.

Из вышеприведенных виртуальных опытов можно сделать основополагающий вывод: энергия от внешнего источника увеличивает (уменьшает) энергию опытного тела (вещества). В результате возникает сила гравитационного смещения по вектору, направленному в сторону более энергонасыщенного источника. Данная сила и есть сила притяжения, сила гравитации. На энергетическом уровне Е₁> Е₂ (рис. 2.12, с).

?Е=Е₁-Е₂

Разница ?Е между поступившей энергией и энергией самого тела – это энергия, которая тратится на тяготение данного тела к источнику энергии.

2.9.2. Эффект Пельтье, Томсон и температура

В 1856 г. У. Томсон (лорд Кельвин) выдвинул гипотезу, что теплота, аналогичная теплоте эффекта Пельтье, должна выделяться (поглощаться) при прохождении тока по однородному проводнику, вдоль которого имеется градиент температуры [10, с. 268]. Эффект Пельтье заключается в том, что при протекании электрического тока через разнородные спаи (соединения) двух металлов в одном спае происходит выделение теплоты, а в другом – поглощение. Предсказанный Томсоном эффект впоследствии был подтвержден экспериментально и получил название «явление Томсона», которое записывается следующим выражением:

Q – количество теплоты, выделяющееся в единицу времени в проводнике длиной dl.

I – сила тока, d?/dl – градиент температуры, ? – коэффициент, называемый коэффициентом Томсона.

Последуем за лордом Кельвином так же, как он в свое время последовал за Пельтье, и используем вышеприведенную формулу для наших целей, но значение ее будет совершенно иным. Для чего заменим линейный размер тела на его объем:

k – коэффициент пропорциональности.

Сила тяготения dF, действующая в единицу времени в элементе вещества с объемом dV, пропорциональна интенсивности излучения I и градиенту температуры d?/dV.

Гравитация – это взаимообмен квантами энергии.

2.9.3. Тепловая машина

Приведенные выше примеры показывают, что мы фактически создали тепловую машину, работающую по циклу Карно7 (рис. 2.13).

В начале процесса кубик имел комнатную температуру, точка (А). Затем мы его привели в контакт с охладителем (ВС), который изотермически (при постоянной температуре) отнял у него некоторое количество теплоты. При этом объем кубика уменьшился. Далее мы вынули кубик из охладителя и нагрели до комнатной температуры (DA). Цикл закончился.

В начале второго цикла кубик привели в контакт с нагревателем (EF), который изотермически передал ему порцию теплоты. Кубик расширился. Закончили цикл, охладив кубик при комнатной температуре (DA).

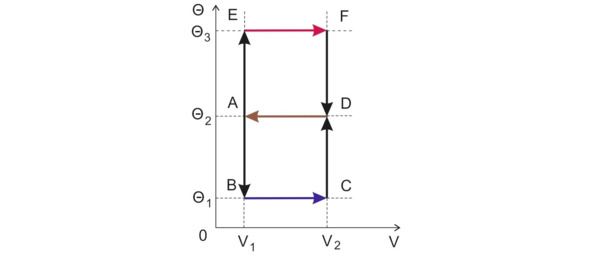
Рис. 2.13. Кубик Рубика и тепловая машина.

Если данный кубик заранее соединить, например, с поршнем, то он бы совершил работу. Но что это за работа – хуже вышивания!

Для того чтобы возникло тяготение, направленное по какому-либо результирующему вектору, необходимо нарушить тепловое равновесие или относительно земли совершить работу по увеличению потенциальной энергии (поднять тело на высоту).