Пространство Минковского

Пространство Минковского

Тогда нарушается закон причинно-следственной связи, закон, от которого я совершенно не собирался отказываться из-за каких-то паршивых попугаев, да еще дохлых вдобавок…

Аркадий Стругацкий, Борис Стругацкий «Понедельник начинается в субботу»

Как мы уже отметили, в СТО пространство и время нужно рассматривать как единый четырехмерный континуум – его называют пространством Минковского. Тогда непривычные (для бытового восприятия) свойства теории объяснять и интерпретировать значительно легче. Пространство Минковского представляют в виде диаграммы с временной и пространственными осями. На временной оси в качестве отсчета используется время, умноженное на скорость света – ct, это упрощает анализ, поскольку все данные имеют одинаковую размерность. Пространственные координаты, также для простоты, часто представлены только координатой x, хотя, конечно, подразумеваются все три. Кроме того, в отличие от общепринятых диаграмм, здесь роль функции играет время, а аргумента – пространственные координаты.

Диаграмма пространства Минковского, точно так же, как обычные диаграммы, используется для отображения в виде графика пути, который проходит материальная частица с течением времени. Если частица движется равномерно и прямолинейно – ее путь будет прямой линией, а котангенс угла наклона к оси x равен скорости частицы в долях скорости света. На рис. 5.2 изображен путь такой частицы от начала координат до точки A. Прямые, направленные под углом 45°, отображают пути фотонов, движущихся со скоростью света как через начало координат, так и через точку А в разные стороны. Позже мы определим такие «фигуры» как световые конусы. Движение частицы от точки А возможно только внутри конуса, поскольку ее скорость не может превышать световую.

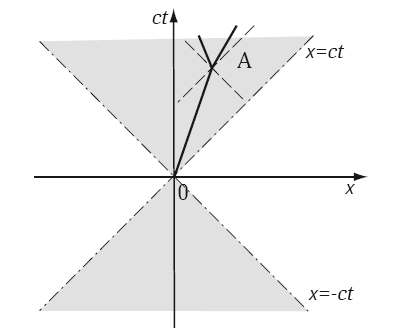
Рис. 5.2. Путь частицы на диаграмме пространство-время

Если частица движется произвольно, то ее путь будет представлен кривой, а котангенс угла наклона касательной к оси x в какой-либо точке будет равен скорости частицы в момент, соответствующий этой точке.

Как в СТО, так и в общей теории относительности (мы увидим это позднее) ключевым понятием является метрическое пространство. Под этим понимается некое множество точек, переход между которыми осуществляется непрерывным образом и определено понятие расстояния между ними. Вспомним обычное пространство Евклида. Квадрат расстояния r между началом координат и точкой с декартовыми координатами x, y, z определяется по правилу: r² = x² + y² + z².

Эта величина всегда положительная, за исключением случая, когда длина равна нулю.

Пространство Минковского тоже метрическое. Однако в нем расстояние между двумя точками называется интервалом и определяется непривычным образом. Квадрат интервала s между началом координат и какой-либо точкой 4-мерного пространства-времени (рис. 5.2) определяется по правилу:

s² = c²t² – x² – y² – z² = c²t² – r².

Временную координату ct и пространственные координаты Декарта x, y, и z, представляющие единую координатную сетку в пространстве Минковского, обычно называют координатами Лоренца. Как видно, временная и пространственные части в определении интервала входят с разными знаками. Из-за этого квадрат интервала может быть положительным, нулевым и даже отрицательным. Пространства, в которых расстояния определяются таким образом, называются псевдоевклидовыми.

Итак, пространство Минковского – это псевдоевклидово метрическое пространство, объединяющее время (длительность) и пространство (протяженность, 3-мерное пространство Евклида).

Точки в пространстве Минковского называют событиями или мировыми точками. Таким образом, каждой мировой точке соответствует момент времени и точка в 3-мерном пространстве. А интервал – это расстояние между двумя мировыми точками или, в ряде интересных случаев, промежуток времени между двумя событиями.

Теперь попытаемся понять, как в рамках исходной системы отсчета в пространстве Минковского выглядит другая инерциальная система отсчета. Оси 0ct и 0x (см. рис. 5.2) в исходной системе образуют базис. Путь наблюдателя, связанного с исходной системой, направлен вдоль оси 0ct. Для него же ось 0x и параллельные ей линии – это сечения одновременности. Наблюдатель другой инерциальной системы движется прямолинейно и равномерно по отношению к первой. Тогда ясно, что его путь направлен вдоль наклонной прямой, например, 0А на рис. 5.2. Для движущегося наблюдателя сечения одновременности также наклонятся. Остается сделать вывод: чтобы перейти к базису движущейся инерциальной системы отсчета нужно осуществить поворот исходного базиса. При этом угол поворота соответствует относительной скорости между системами. Вспомним, что две системы отсчета связаны преобразованиями Лоренца. Именно поэтому такие повороты базиса называют лоренцевыми вращениями.

На рис. 5.3 на диаграмме пространства Минковского изображен базис неподвижной системы K с нештрихованными координатами, и базис движущейся в направлении оси 0x со скоростью V инерциальной системы отсчета K’ с штрихованными координатами. Теперь выпишем преобразования Лоренца от одних координат к другим:

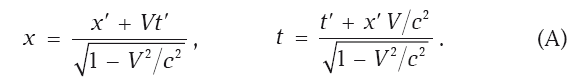
Преобразования дают возможность заключить, что обе системы отсчета эквивалентны. Действительно, если выразить штрихованные координаты через нештрихованные, то получим те же самые преобразования:

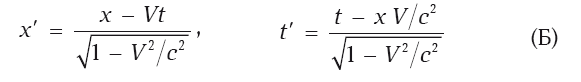
с заменой знака «плюс» перед V на «минус» – по отношению к штрихованной системе нештрихованная движется в противоположном направлении.

Одно из достоинств геометрической интерпретации пространства Минковского состоит в том, что лоренц-инвариантность выражается в инвариантности относительно лоренцевых вращений. В частности, значение интервала, записанного выше, не изменяется после поворота базиса, хотя теперь выражается через новые (штрихованные) координаты нового базиса. Чтобы убедиться в этом нужно лоренцевы преобразования (А) подставить в выражение для квадрата интервала, записанного выше. В результате получим

s² = c²t?² – x?² – y?² – z? ² = c²t?² – r?².

то есть s = s’.

В инвариантности интервала нет ничего удивительного – это лишь геометрическое свойство пространства Минковского, а не следствие каких-то принципов. Действительно, поскольку интервал – это длина в метрическом пространстве, то эта величина не зависит от способов измерения (использования той или иной координатной сетки). Замечательно другое – известные геометрические свойства псевдоевклидовых пространств оказались весьма полезными для описания СТО.

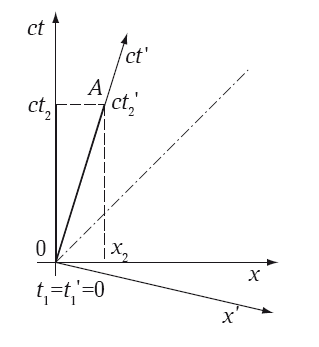
Рис. 5.3. Переход к другой инерциальной системе на диаграмме пространства Минковского

Эффекты сокращения длины, замедления времени, сложение скоростей в СТО являются следствием лоренц-инвариантности. Остановимся на первых двух. Рассмотрим линейку, собственная длина которой l₀ – это длина в ее системе покоя. Пусть система покоя для выбранной линейка – это система K’, которая движется относительно нас (системы K) со скоростью V. Тогда, если концы линейки имеют координаты

x₁? и x₂?, то l₀ = x₂? – x₁?.

Определим длину этого отрезка с точки зрения наблюдателя системы K. Для этого нужно в один и тот же (!) момент времени t определить координаты концов линейки x₂ и x₁ в системе K. Тогда для нас длина линейки буде иметь величину l = x₂ – x₁. Чтобы определить каждое из значений x₂ и x₁ через соответствующие штрихованные координаты используем первую часть преобразований Лоренца (Б) каждый раз с одним и тем же значением t. Затем составим разницу и получим 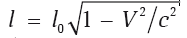, то есть для нас (покоящейся системы K) движущаяся линейка становится короче.

Подтвердим вывод о замедлении времени. Находясь в системе K, будем отслеживать ход часов в системе K?, которые находятся в точке x?. Для нас часы в системе K идут одинаково во всех точках, поэтому часы системы K? можно сравнивать с любыми нашими. Не теряя общности, можно предположить, что x? = 0 и моменты первого сравнения в обеих системах также нулевые: t₁? = t₁ = 0. Вопрос в том, как начнут разниться показания в любой следующий момент сравнения t₂ (а для системы K? – t₂?). Теперь удобнее использовать вторую часть преобразований Лоренца (А). Получаем 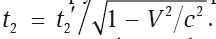 . Как видно, показания часов в нашей системе K будут больше, чем в K?, хотя в обоих случаях отсчет начинался с нуля. Таким образом, движущиеся часы идут медленнее.

На этом этапе важно сделать замечание. Мы все больше убеждаемся, что пространство и время физически объединены в единое целое – пространственно-временной континуум. Действительно, и пространственные, и временные координаты участвуют в единых преобразованиях; инвариантная величина интервал построена как из временных промежутков, так и из пространственных отрезков. Несмотря на это, и пространство, и время сохраняют свою физическую сущность – протяженность и длительность. Формально это различие состоит в том, что временная часть входит в интервал со знаком «плюс», а пространственная – со знаком «минус».

Мы уже отметили, что квадраты интервалов могут быть положительными, нулевыми и даже отрицательными. Для положительных – временная часть превосходит пространственную, и они называются времениподобными. Нулевые соответствуют распространению света и называются светоподобными; совокупность светоподобных, представляющая распространение световых лучей из какой-либо мировой точки, образует, так называемый, световой конус в пространстве Минковского. На рис. 5.4 такой световой конус относится к началу координат и делит пространство-время на две части: внутри и вне конуса. Наконец, для отрицательных квадратов интервалов, пространственная часть превышает временную, и они называются пространственноподобными.

Для нас более интересны времениподобные интервалы. Почему? Отрезок прямой 0A, соединяющий мировую точку внутри конуса и начало координат на рис 5.4 вполне можно интерпретировать как путь материальной частицы, движущейся прямолинейно и равномерно. Скорость ее меньше скорости света, и поэтому путь находится внутри конуса. Квадрат интервала между точкой А и началом координат s² = c ²t ² – xА²  – положительный, и это относится ко всем мировым точкам внутри конуса, скажем A?. Наклон соответствующих отрезков пути меньше, чем у светового конуса. Если бы мы попытались интерпретировать отрезки пути с наклоном больше, чем у светового конуса, как путь материальной частицы, то нужно было бы говорить о скоростях больших скорости света. Но для материальной частицы это невозможно, мы об этом еще скажем.

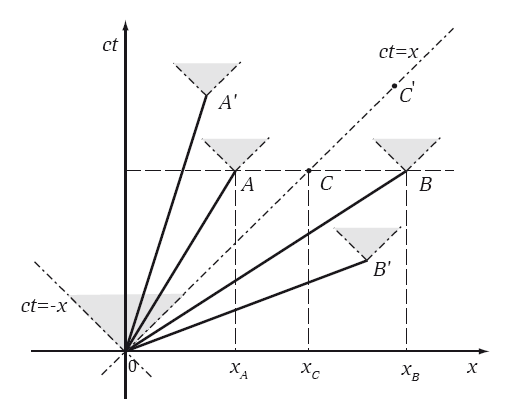
Рис. 5.4. Интервалы в пространстве Минковского

Продолжим обсуждение времениподобных интервалов. На рис. 5.4 отрезок на временной оси, скажем, от начала координат до точки ct, определяет, конечно, такой интервал. В чем его смысл? Он соответствует наблюдателю, который покоится в этой инерциальной системе отсчета, а соответствующий интервал определяет промежуток времени жизни наблюдателя между этими событиями: s = ct. После лоренцева вращения этот отрезок станет наклонным. (Другими словами: в другой инерциальной системе этот наблюдатель будет двигаться прямолинейно и равномерно.) Однако, в силу лоренц-инвариантности значение интервала для этого отрезка не изменится, хотя примет другое выражение: s = (c²t?² – x?²)^1/2. Это позволяет сделать важный вывод, давайте его зафиксируем:

Времениподобный интервал s между двумя событиями на мировой линии наблюдателя определяет промежуток собственного времени наблюдателя между этими двумя событиями: ?=s/c. Еще и поэтому такие интервалы называют времениподобными.

Перейдем к обсуждению светоподобных интервалов. Отрезок прямой 0C на конусе на рис. 5.4 вполне можно интерпретировать как путь фотона (луча света), движущего прямолинейно и равномерно со скоростью света. Действительно, лучу света отвечают прямые x = ct и x = – сt. Это как раз подтверждает, что интервал между любыми двумя мировыми точками на такой прямой равен нулю, т. е. светоподобный. Например, между началом координат и точкой C: s² = c²t ² – x_с² = 0, или между началом координат и точкой C?, или между точками C и C? и т. д.

А теперь дадим еще одно определение. Множество мировых точек, описывающее движения в зависимости от времени материальной частицы (в том числе и безмассовой, как фотон) на пространственно-временной диаграмме (в данном случае на диаграмме пространства Минковского) называется мировой линией. Если интервалы для любых двух точек на прямых мировых линиях времениподобны или светоподобны, то сами линии, соответственно, времениподобные или светоподобные. Конечно, мировые линии могут быть и искривленными. В этом случае, чтобы они соответствовали реальным частицам необходимо, чтобы углы наклона всех касательных не превышали угол наклона светового конуса. Тогда скорость частицы не превысит световую.

Также не нужно путать понятие мировой линии с обычной траекторией частицы в 3-мерном пространстве. Мировая линия – это путь на пространственной-временной диаграмме, траектория – это след, который оставляет зверек в зимнем лесу.

Наконец, обсудим пространственноподобные интервалы. Если мы возьмем любую мировую точку вне конуса, скажем B, как на рис 5.4, то квадрат интервала между этой точкой и началом координат s² = c²t² – x_В² будет отрицательным, и он будет как раз пространственноподобным. Точно так же, это относится ко всем мировым точкам вне конуса, скажем B?, поскольку пространственная часть интервала превышает временную. Наклон соответствующих отрезков больше, чем у светового конуса.

При лоренцевых вращениях в силу инвариантности все интервалы сохранят свои значения, а значит и тип, к которому относятся. То есть все мировые точки, которые были внутри конуса, там и останутся, то же относится к точкам вне конуса. Интересным является поведение светового конуса при таких вращениях. Поскольку скорость света во всех инерциальных системах отсчета одинакова, то угол светоподобных отрезков не изменится (!), а это значит, что световой конус останется на месте.

На рис. 5.3 световой конус после лоренцева вращения не изменил своего положения, он относится как к покоящейся системе отсчета с нештрихованными координатами, так и к движущейся – со штрихованными.

Теперь определим еще одно важное понятие. Если для интервала между двумя событиями s² ? 0, то эти события могут быть соединены мировой линией, которая отвечает реальной частице или лучу света. Такие два события называют причинно связанными.

Если для интервала между двумя событиями s² < 0, то как бы мы не соединяли эти мировые точки непрерывными линиями, найдутся участки, где наклон касательной превышает наклон светового конуса. Такая линия не может быть отнесена к мировой линии какой-либо реальной частицы, а события, для которых s² < 0, называют причинно несвязанными.

Чтобы чувствовать себя уверенней, используя свойства пространства Минковского, полезно осознать, как сравниваются времениподобные интервалы на пространственно-временной диаграмме. Снова возьмем отрезок на временной оси от начала координат до момента t, квадрат его интервала – s² = c²t². Затем рассмотрим наклонный отрезок прямой (времениподобной), также от начала координат до какой-либо мировой точки, но с той же временной координатой t (например, точки A, рис. 5.4). Его квадрат интервала – это s² = c²t²– x_A². Мы видим, что интервал наклонного отрезка меньше, чем интервал вертикального для одинакового значения t!

Это выглядит парадоксально, ведь визуально все наоборот. Но вспомним, что интервал – это не длина траектории, а время, которое в движущейся системе отсчета (наклонный отрезок) течет медленнее, чем в покоящейся. Действительно (рис. 5.3), из преобразований Лоренца следует, что время t?₂ движущихся часов меньше времени t₂ покоющихся. Ясно, что интервал наклонного отрезка станет еще меньше, если мы увеличим наклон. Если наклон сравняется с наклоном светового конуса, то интервал обратится в нуль.

В заключение перечислим основные понятия, определенные только что, и утверждения, важные для понимания свойств пространства Минковского:

• метрическое пространство – множество точек, переход между которыми осуществляется непрерывным образом и введено правило определения расстояния между точками;

• мировая точка или событие – точка на диаграмме пространства Минковского (в 4-мерном пространстве-времени);

• мировая линия – совокупность мировых точек на диаграмме пространства Минковского, описывающая движение в зависимости от времени материальной массивной или безмассовой частицы;

• пространство Минковского – псевдоевклидово метрическое пространство, в котором связь между пространственными расстояниями и промежутками времени, разделяющими события, определяется интервалом, сохраняющимся при переходе от одной инерциальной системы отсчета к другой;

• интервал времениподобный, если его квадрат положительный; в этом случае он эквивалентен промежутку собственного времени наблюдателя, следующего от одного события к другому прямолинейно и равномерно;

интервал светоподобный, если его квадрат равен нулю;

интервал пространственноподобный, если его квадрат отрицательный;

• световой конус в данной мировой точке – совокупность всех светоподобных прямых, проходящих через эту точку;

• причинно связанные события – события, которые могут быть соединены мировой линией, все касательные к таким линиям имеют наклон, не превышающий наклона светоподобных прямых;

• лоренцевы вращения – переход в пространстве Минковского из одной инерциальной системы отсчета в другую;

Теперь, используя представления о пространстве Минковского, продвинемся дальше.

Данный текст является ознакомительным фрагментом.