8. Модели Фридмана и критическая плотность

8. Модели Фридмана и критическая плотность

В основном тексте было сказано, что каждой из моделей Фридмана: открытой, плоской и закрытой, соответствуют свои значения плотности энергии ? или плотности массы ? в соответствии с определением ? = ?с ². Плоской модели соответствует критическая плотность ?_кр = ?_крс ², открытой – ? < ?_кр, а закрытой – ? > ?_кр. Напрашивается очевидный вопрос: в каком мире мы живем?

Рассмотрим ситуацию несколько подробнее. Одно из уравнений Фридмана можно привести к виду:

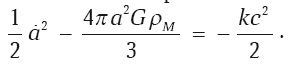
Здесь ?_M означает плотность массы всей материи Вселенной, которую обычно записывают в виде суммы ?_M = ?_m + ?_dm + ?_de, где вклад представлен обычной материей (барионы, излучение), темной материей и темной энергией. Величина k называется знаком кривизны и определяет тип модели Фридмана: гиперболическому пространству соответствует k = –1, плоскому – k = 0, замкнутому – k = +1. В ходе эволюции Вселенной знак кривизны не меняется.

Теперь вспомним, что постоянная Хаббла H= a /a, и нормируем это уравнение на ?_кр = 3H ²/8?G. Тогда оно приобретет форму:

?_M = 1 + ?_c.

Здесь ?_M = ?_M/?_кр и ?_c = kc ²/(a ²H ²).

Как видно, величина ?_c описывает отклонение от единицы в ту либо другую сторону отношения ?_M, а конкретное значение ?_c определяет знак и величину кривизны пространства. Если отклонения нет, то кривизна пространства нулевая. Таким образом, вопрос о геометрии пространства решается, если известно значение ?_M.

Однако определить ?_M напрямую эмпирически невозможно. Поэтому, наоборот, сначала с помощью наблюдений определяют кривизну пространства. Это делается различными способами. Наибольшим доверием пользуется анализ анизотропии реликтового излучения. Другой способ основан на изучении видимой светимости (блеска) сверхновых известного типа в далеких галактиках, независимом определении расстояний до них и сопоставлении этих данных. Также информацию о типе и величине кривизны получают, исходя из картины крупномасштабной структуры Вселенной.

Кривизна трехмерного пространства оказывается весьма малой, радиус кривизны, по крайней мере, в 10 раз превышает размеры наблюдаемой части Вселенной. Это соответствует отклонению плотности всей материи от критической | ?_c | < 0,01. Если плотность массы обычной материи ?_m и темной материи ?_dm известны из эмпирических данных, то плотность темной энергии ?_de не известна. Фактически она определяется расчетным путем из соотношения ?_M ? ?_кр. И, наконец, поскольку оценка кривизны приблизительна, то пока нельзя сказать какая именно из моделей Фридмана соответствует реальному миру.

Данный текст является ознакомительным фрагментом.