Глава 11 Модели звезд

Глава 11 Модели звезд

В § 6 мы получили основные характеристики звездных недр (температура, плотность, давление), используя метод грубых оценок величин, входящих в уравнения, описывающие состояния равновесия звезд. Хотя эти оценки дают правильное представление о физических условиях в центральных областях звезд, они, конечно, совершенно недостаточны для понимания сходства и различия между разными звездами. Например, для решения важного вопроса, какая именно ядерная реакция (протон-протонная или углеродно-азотная) ответственна за излучение той или иной конкретной звезды, необходимо более совершенное знание условий в ее недрах. Наконец, остается пока не рассмотренной основная задача: каков физический смысл диаграммы Герцшпрунга — Рессела? Эта задача, как мы увидим ниже, теснейшим образом связана с проблемой эволюции звезд. Хотя запасы ядерной энергии в недрах звезд очень велики, все же их нельзя считать неисчерпаемыми. Рано или поздно (в зависимости от массы звезды) они подойдут к концу. Что будет при этом происходить со звездой? Как она будет менять свои свойства?

Чтобы понять связь между разными звездами и причины наблюдаемых различий между ними, надо хорошо знать мгновенное состояние разных звезд, как бы «моментальную фотографию» структуры их недр. Точно так же как реальные физические процессы можно представить как последовательность «квазистатических» состояний, очень медленный процесс эволюции звезды (обусловленный истощением запасов ее ядерного горючего) можно представить как последовательность ее равновесных конфигураций. Такие конфигурации, получаемые теоретическим, расчетным путем, носят название «звездных моделей».

Под «звездной моделью» понимается совокупность таблиц (или графиков), дающих «идеализированное» распределение плотности, температуры, давления, химического состава вещества звезды для разных глубин, выраженных в долях ее радиуса. Следует подчеркнуть, что такая модель отнюдь не тождественна реальной звезде. Все же хорошо рассчитанная модель, правильно учитывающая основные физические законы, определяющие структуру звезды, может (и должна!) давать в основном верное представление о свойствах вещества звездных недр. Было бы ошибочно считать, что расчет звездных моделей содержит в себе элемент произвола. Наоборот, он непрерывно и жестко контролируется в процессе самих вычислений. И, наконец, он после своего завершения должен находиться в полном согласии с наблюдаемыми свойствами «моделируемых» звезд. Например, если речь идет о расчете модели звезды главной последовательности, у рассчитанной модели должно выполняться соотношение «масса — светимость».

Если бы была возможность непосредственно наблюдать внутренние области звезд, не было бы надобности в построении их моделей. Ведь структуру туманностей, которые «видны насквозь», мы получаем непосредственно из оптических и радиоастрономических наблюдений. Увы, недра звезд скрыты от нас гигантской толщей звездного вещества и почти нет шансов «увидеть», что там происходит. Мы подчеркнули слово «почти», так как все-таки имеется одна возможность непосредственного наблюдения звездных недр, о которой было рассказано в § 9. Итак, построение звездных моделей есть процедура вынужденная, иначе мы не могли бы делать количественных выводов об основных тенденциях развития большей части вещества во Вселенной.

Как же рассчитываются звездные модели? Прежде всего основой таких расчетов являются физические законы, определяющие равновесную конфигурацию звезды. Об этих законах уже шла речь в § 6 и 7. Это, во-первых, условие гидростатического равновесия, которое должно выполняться для каждого элемента объема внутри звезды (см. формулу (6.1)). Во-вторых,— так называемое «условие лучистого равновесия», описывающее перенос излучения из недр звезды, к ее поверхности (см. уравнение (7.10)). Далее необходимо учитывать, как меняется непрозрачность звездного вещества в зависимости от изменения температуры и плотности, а также зависимость давления от плотности и температуры, т. е. «уравнение состояния». Для вещества «нормальных» звезд последнее описывается уравнением Клапейрона, а для белых карликов — формулой (10.1). Необходимо учитывать и очень сильную зависимость скорости выделения ядерной энергии от температуры (см. стр. 246). Кроме того, считаются заданными такие основные параметры «моделируемых» звезд, как их масса, светимость и радиус.

Ввиду сложности системы уравнений, описывающих состояние звезд, расчет модели не может быть сделан аналитически, т. е. по готовой, пусть даже очень громоздкой, формуле. Успех достигается только численным методом решения этих уравнений (являющихся, кстати, дифференциальными). Предполагается, что модель звезды сферически-симметричная, т. е. все характеристики какого-нибудь элемента ее объема (температура, плотность и пр.) зависят только от расстояния этого элемента от центра звезды. В чем же идея численного метода расчета? Представим себе, что звезда состоит из очень большого числа концентрических сферических слоев. В пределах каждого слоя (если он только выбран достаточно тонким) значения указанных характеристик можно считать постоянными. Зададим значения давления и температуры в центре звезды. Условия гидростатического равновесия позволят тогда найти давление на поверхности первой (самой внутренней) сферы. Далее, путем расчетов определяем, пользуясь формулой Клапейрона, температуру в центре. Затем, зная зависимость скорости ядерного энерговыделения от температуры и используя уравнение для переноса лучистой энергии (7.10), мы получим температуру на поверхности шаровой сферы, а затем, пользуясь формулой Клапейрона,— плотность. Такая процедура (как видим, довольно сложная!) позволяет по данным температуре, плотности и давлению в центре звезды получить те же основные характеристики на некотором относительно малом расстоянии от центра. После этого тем же методом процедура повторяется и получается значение характеристик звездного вещества, на поверхности второй сферы, радиус которой вдвое больше, чем у первой. Так, шаг за шагом, получается «разрез» всей звезды, т. е. значения основных характеристик ее вещества в зависимости от расстояния от центра. Для того чтобы расчет модели увенчался успехом, толщины воображаемых сфер, на которые разбивается звезда, должны быть достаточно малы. С другой стороны, конечно, непрактично делать их слишком маленькими, что привело бы к неоправданно большому увеличению объемов расчета. Практически количество таких сфер бывает порядка нескольких сотен, иногда даже нескольких тысяч.

Масса рассчитанной модели получается как результат суммирования «парциальных» масс, заключенных в пределах элементарных сфер. Учитывая «производство» термоядерной энергии в разных слоях, можно по окончании расчета получить теоретическую светимость звездной модели.

Раньше такие расчеты моделей выполнялись вручную, на арифмометрах. Однако последние три десятилетия расчеты моделей производятся преимущественно на электронных вычислительных машинах. Резкое увеличение «производительности труда», помимо облегчения работы вычислителя, позволило широко варьировать различные параметры, входящие в расчет, и выбирать из них те, которые дают разумные и непротиворечивые модели. В частности, условием непротиворечивости модели, дающей некоторые значения радиуса, массы и светимости звезды, является выполнение закона «масса — светимость», если речь идет о расчете модели звезды главной последовательности. Отчего же могут получиться в процессе расчетов модели, явно несоответствующие реальным звездам? В значительной степени это происходит из-за большой неуверенности в знании химического состава недр звезды, модель которой рассчитывается. Приходится при расчетах работать «методом проб и ошибок», отбрасывая такие предположения о химическом составе, которые приводят к явно несуразным результатам. Имеется и еще довольно специфическая причина расхождения между основными расчетными характеристиками модели звезды (т. е. ее массы, светимости и радиуса) и наблюдаемыми характеристиками соответствующей реальной звезды. Дело в том, что при некоторых условиях процесс переноса энергии в недрах звезды может менять свой характер. Например, перенос энергии путем лучеиспускания может смениться конвективным переносом. Это бывает по разным причинам. Так, если по мере погружения в глубину температура начинает расти довольно резко, лучеиспускание, возможности которого «ограничены», уже не в состоянии обеспечить транспортировку всей выделяющейся в недрах звезды энергии. Наступает неустойчивость, и доминирующим механизмом переноса энергии становится конвекция. Об этом речь шла уже в § 8. Поэтому в процессе вычислений, которые выполняются «шаг за шагом», следует внимательно следить и контролировать, как ведет себя механизм переноса энергии в строящейся модели звезды.

Следует также иметь в виду, что химический состав звезды, определяемый параметрами X, Y , Z (см. § 7), не останется постоянным для всей звезды, а может систематически и притом радикально отличаться в ее разных частях. Например, в центральной области звезды, из-за «выгорания» водорода у сравнительно старых звезд, X может быть значительно меньше, чем на периферии. Модели звезд, учитывающие это обстоятельство, носят название «неоднородных». Такие модели представляют значительный интерес, так как хорошо отражают действительность.

Приводя пример, как строится модель звезды, мы рассматривали такое построение идущим от центра к периферии. Можно и даже часто более удобно рассчитывать модель от поверхности к центру. В этом случае задаются радиус и светимость (или температура) звезды. Естественно, что по окончании расчета суммарная масса сферических слоев должна быть равна массе звезды. Неверные методы расчета могут привести к «исчерпанию» массы модели звезды задолго до того, как расчеты дойдут до центра. Автор когда-то наблюдал такой любопытный феномен в работах некоторых начинающих специалистов в области внутреннего строения звезд...

Рис. 11.1: Модель массивной звезды главной последовательности.

В результате большой работы, проделанной астрофизиками-теоретиками, специалистами по внутреннему строению звезд, в настоящее время имеется много моделей звезд. Эти модели охватывают звезды, занимающие различные места на диаграмме Герцшпрунга — Рессела. Мы сейчас обсудим основные особенности моделей, соответствующие звездному населению нашей Галактики. Прежде всего представляют интерес модели звезд главной последовательности на диаграмме Герцшпрунга — Рессела. Оказывается, что структура звезд верхней части этой последовательности (горячие массивные объекты высокой светимости) значительно отличается от структуры красных карликов, заполняющих ее нижнюю правую часть. На рис. 11.1 наглядно представлена структура массивной горячей звезды. Эта модель была рассчитана для звезды, масса которой в 10 раз больше солнечной, радиус в 3,6 раза больше, а светимость (болометрическая) в 3000 раз превосходит светимость Солнца. Это означает, что моделируемая звезда имеет спектральный класс В0, причем температура ее поверхности около 25 000 К. Как показывают расчеты, в центральной части звезды перенос энергии осуществляется путем конвекции. Радиус конвективной зоны составляет около 25% радиуса звезды. Эта зона содержит в себе также около 25% полной массы звезды. Характерна довольно большая концентрация плотности вещества по направлению к центру. В самом центре плотность примерно в 25 раз превосходит среднюю плотность звезды и близка к 7 г/см³. Центральная температура довольно высока — около 27 миллионов кельвинов, т. е. примерно в два раза больше, чем у Солнца. Качественно этого и следовало ожидать согласно простой формуле (6.2), хотя температура оказалась несколько ниже, чем рассчитанная по этой формуле. Модель не очень сильно зависит от принятого химического состава звезды (X = 0,90, Y = 0,09, Z = 0,01). Любопытно, в каком направлении будет меняться структура звезд такого типа, если уменьшать массу? Расчеты показывают, что при этом, во-первых, в соответствии с формулой (6.2) будет уменьшаться центральная температура, во-вторых, будут уменьшаться относительные размеры конвективного ядра. У таких звезд основным источником энергии является углеродно-азотная реакция. Как мы видели, скорость этой реакции очень сильно растет с ростом температуры (см. формулу (8.3)). Поэтому для «отвода» выделяющегося при этой реакции огромного количества энергии уже недостаточно одного лишь лучистого ее переноса. В этом случае транспортировку энергии берет на себя конвекция. Это и объясняет существование у таких звезд более или менее протяженных конвективных ядер в центральных областях. Схема на рис. 11.1 представляет структуру типичных звезд верхней части главной последовательности. На рис. 11.2 схематически представлена модель красного карлика с массой 0,6, светимостью 0,56 и радиусом 0,64 солнечного. Следовательно, речь идет о модели карликовой звезды спектрального класса К — М. Обращает на себя внимание то обстоятельство, что структура такой звезды значительно отличается от структуры массивных, горячих звезд верхней части главной последовательности. Прежде всего, в центральных частях карликовых звезд уже совсем нет конвективной зоны. Наоборот, в наружных слоях таких звезд перенос энергии осуществляется преимущественно путем конвекции. В приведенной на рис. 11.2 модели конвективная зона занимает наружную часть звезды, причем там сосредоточено примерно 10% ее массы. Причина отличия в структуре звезд нижней части главной последовательности от структуры массивных горячих звезд кроется в сравнительно низкой температуре недр карликовых звезд. Из-за этого растет непрозрачность звездного вещества и перенос вырабатываемой в центре звезды энергии путем излучения становится затруднительным. На помощь приходит конвекция. Концентрация вещества к центру у карликовых звезд не так велика, как у горячих гигантов. Центральная плотность уже только в 20 раз превосходит среднюю, хотя абсолютное значение центральной плотности гораздо выше, около 60 г/см³. В согласии с формулой (6.2) центральная температура в рассматриваемой модели карликовой звезды сравнительно низка — около 9 миллионов кельвинов. При такой температуре энергетика карликовых звезд обеспечивается только протон-протонной реакцией.

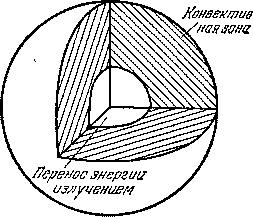Рис. 11.2: Модель красного карлика.

Солнце является довольно типичной звездой средней части главной последовательности. Вместе с тем модель внутреннего строения Солнца по понятным причинам представляет для нас особый интерес.

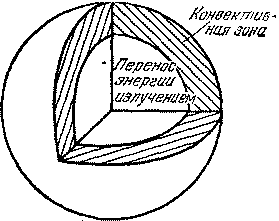Рис. 11.3: Модель Солнца.

В последние годы было рассчитано несколько моделей Солнца, отличающихся численными значениями некоторых параметров расчета (прежде всего химического состава). Имеется еще одна важная особенность расчета моделей Солнца. Особенностью моделей звезд верхней и нижней частей главной последовательности, которые приведены на рис. 11.1 и 11.2, является их однородность. Это означает, что химический состав звезды предполагается постоянным во всем объеме звезды. Последнее предположение вполне естественно для карликовых звезд малой массы и сравнительно низкой светимости, время пребывания которых на главной последовательности превышает возраст Галактики. Поэтому в центральных частях этих звезд израсходована только малая часть первоначального «запаса» водородного «горючего». Что касается массивных звезд верхней части главной последовательности, то приведенная на рис. 11.1 модель относится к сравнительно молодым звездам этого типа. Иное дело Солнце. Возраст Солнца известен — около 5 миллиардов лет. За такой огромный срок уже можно ожидать некоторого уменьшения содержания водорода в центральной части нашего светила, так как заметная часть первоначального запаса водородного горючего Солнца уже израсходована— все-таки Солнце светит очень долго... Тут-то и кроется известная неопределенность в расчете модели Солнца, которая должна быть неоднородной. Какой процент солнечного водорода «выгорел» и в каком объеме? Ведь можно варьировать и объем, и процент «выгоревшего» водорода, что и делается в различных моделях. Любопытно, что центральная температура Солнца получается почти не зависящей от конкретных особенностей различных моделей. Она близка к 14 миллионам кельвинов — значению, которым мы пользовались в § 9. Это означает, что основной термоядерной реакцией в недрах Солнца является протон-протонная реакция, хотя небольшой вклад дает также углеродно-азотный цикл. Для модели, изображенной на рис. 11.3, принято, что в центральной области X = 0,50 и плавно растет до тех пор, пока на расстоянии от центра, равном 0,25 радиуса, становится равным около 75%, после чего, вплоть до самой поверхности, остается постоянным. Так же как и у красных карликов, у этой модели Солнца нет конвективного ядра, однако размеры наружной конвективной зоны значительно меньше. Заметим, что эта зона содержит всего около 2% массы Солнца. Центральная плотность Солнца довольно велика — она больше, чем у моделей звезд как верхней, так и нижней частей главной последовательности и равна 135 г/см³, что почти в 100 раз превосходит среднюю плотность. Такая большая концентрация массы к центру естественно объясняется частичным «выгоранием» водорода в центральных областях нашего светила. В сильнейшей степени этот эффект, как мы увидим, проявляется у красных гигантов. Развитие науки в нашу эпоху открыло совершенно неожиданную возможность уточнения модели Солнца, о чем уже шла речь в § 9.

Специфической особенностью субкарликов является очень низкое содержание тяжелых элементов. Об этом уже говорилось в § 1. Поэтому при расчете моделей таких звезд величина Z полагается равной нулю. Так как содержание тяжелых элементов имеет решающее значение для непрозрачности звездного вещества, то при малом Z прозрачность вещества субкарликов должна быть очень высокой, даже если температура сравнительно низка. Поэтому лучеиспускание достаточно эффективно переносит энергию и нет необходимости в развитии конвекции. Центральная температура таких звезд довольно чувствительно зависит от принятого содержания гелия, которое толком не известно.

Однако, пожалуй, самой интересной структурой обладают красные гиганты. На рис. 11.4 приведена модель довольно типичного красного гиганта, масса, радиус и светимость которого превосходят солнечные соответственно в 1,3, 21 и 225 раз.

В самой центральной части звезды-гиганта находится маленькое ядро, температура которого очень высока — 40 миллионов кельвинов. В этом ядре практически нет водорода — он уже весь «выгорел», превратившись в гелий. Вместе с тем температура там еще недостаточно высока для «тройной» гелиевой реакции (см. § 8).

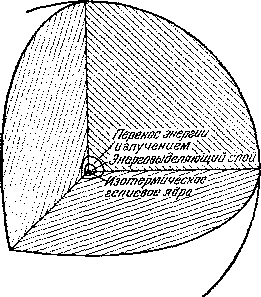Рис. 11.4: Модель красного гиганта.

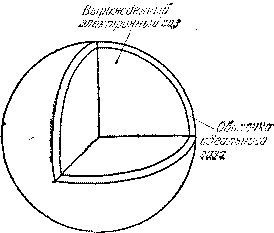Рис. 11.5: Модель белого карлика.

Из-за отсутствия источников энергии температура в области ядра постоянна. Поэтому такое ядро называется «изотермическим». Несмотря на очень малые размеры изотермического ядра (около одной тысячной радиуса звезды), в нем содержится примерно четверть всей массы звезды. Отсюда непосредственно следует, что плотность изотермического ядра огромна — порядка 3 10⁵ г/см³. Это означает, что электронный газ в ядре вырожден (см. § 10). Следовательно, по своим свойствам вещество изотермического ядра красного гиганта не отличается от вещества белых карликов. Они сходны не только по средней плотности, но и по химическому составу и отсутствию ядерных реакций. Поэтому мы имеем все основания утверждать, что в центре красного гиганта находится ... белый карлик! Этот результат имеет большое значение для проблемы происхождения белых карликов, о чем речь будет идти в следующем параграфе.

Вокруг вырожденного изотермического ядра красного гиганта имеется очень тонкая оболочка, где происходят термоядерные реакции углеродно-азотного цикла. Толщина этой оболочки намного меньше радиуса изотермического ядра. В пределах этого тонкого слоя температура вещества резко падает от 40 до 25 миллионов кельвинов. Плотность вещества в оболочке уже в несколько тысяч раз меньше, чем в центре изотермического ядра. Оболочка, в которой происходят ядерные реакции, окружена в свою очередь сравнительно небольшой толщины (около 10% радиуса звезды) слоем, где выделяющаяся в описанном выше слое энергия переносится путем лучеиспускания. Основная же часть наружных слоев красного гиганта, содержащая почти 70% его массы и начинающаяся приблизительно на расстоянии 0,1 его радиуса от центра, находится в состоянии конвекции. Причина образования столь протяженной конвективной зоны — большая непрозрачность вещества — та же, что и у красных карликов. Таким образом, структура красных гигантов отличается крайней неоднородностью.

В противоположность очень сложной структуре красных гигантов структура белых карликов отличается большой простотой. Об этой структуре речь уже шла в § 10. В двух словах: белый карлик— это очень плотный газовый шар, электроны которого вырождены, окруженный сравнительно тонкой оболочкой, из «обычного» газа (рис. 11.5). Парадоксальность ситуации, однако, состоит в том, что, казалось бы столь различные объекты, как красные гиганты и белые карлики, генетически связаны между собой. Об этом речь будет идти в § 13.