9.1. Статистика метеоритных кратеров на небесных телах

9.1. Статистика метеоритных кратеров на небесных телах

Сталкиваясь с планетными телами, малые тела образуют ударные кратеры, популяция которых создает как бы отпечаток популяции малых тел Солнечной системы. Распределение по размерам ударных кратеров на планетных телах с твердой поверхностью является одной из наиболее легко измеряемых (и весьма сложной в интерпретации) характеристик эволюции Солнечной системы. С точки зрения проблемы астероидно-кометной опасности, наблюдаемая частота встречаемости ударных кратеров различного размера является необходимым дополнением к астрономическим наблюдениям малых тел, которые могут столкнуться с Землей.

При известных скоростях столкновения с различными планетными телами (т. е. планетами, их спутниками и другими малыми телами) и знании законов подобия, связывающих размеры ударных кратеров и параметры тел (ударников), их образующих, данные по частоте встречаемости кратеров и ударников могут быть взаимно дополнены. Процедура такого сравнения была разработана в 1960-х гг., и с тех пор постоянно совершенствуется [Hartmann et al., 1981]. Ниже излагаются основные данные о частоте встречаемости кратеров, а также подходы к их интерпретации.

Лунные кратеры. Измерения распределения по размерам лунных кратеров было начато еще по телескопическим наблюдениям и фотографиям [?pik, 1960]. Уже тогда была выявлена главная черта распределения кратеров по размерам — их число N убывает с ростом диаметра кратера D примерно как степенная функция диаметра. Поскольку статистика кратеров, как и многих других объектов, может быть представлена в различных формах, необходимо привести главные из них. Простейшим способом является кумулятивный подсчет числа кратеров N(> D) с размером, больше данного диаметра D.

Тогда типичное распределение ударных кратеров по размерам можно представить в виде

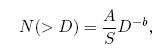
где S — площадь, на которой измерено количество кратеров, b — показатель степенного закона (обычно в диапазоне от 1,5 до 4), A — коэффициент пропорциональности. Кумулятивная форма представления удобна своей простотой, но зачастую приводит к недоразумениям, когда реальный закон распределения отклоняется от простой степенной зависимости.

Инкрементальный способ представления статистики кратеров состоит в подсчете числа кратеров N(D_av), размеры которых заключены в заданном диапазоне размеров D = D₂ ? D₁ при среднем размере, определяемом как среднее арифметическое D_av = (D₁ + D₂)/2 или среднее геометрическое D_av = (D₁ ? D₂)^1/2. Такая статистика описывается выражением

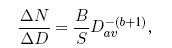
где показатель степенной функции по модулю на единицу больше, чем в кумулятивном законе. Строго говоря, коэффициент пропорциональности B должен быть величиной отрицательной (число кратеров убывает с ростом их размера), однако для практических нужд его практически всегда используют как положительную величину.

После накопления большого опыта в практическом подсчете статистики лунных и марсианских кратеров специально созданная рабочая группа НАСА опубликовала практические рекомендации по стандартизации представления статистики кратеров в инкрементальном виде [Arvidson et al., 1979]. Было рекомендовано, как правило, использовать для инкрементального представления данных не равные интервалы диаметров, а логарифмически равные интервалы, когда отношение D₂/D₁ является величиной постоянной и равной в стандартном случае по умолчанию ?2. В случае постоянства отношения D₂/D₁ показатель степени в инкрементальном законе будет таким же, как и в кумулятивном законе. Поскольку главным сторонником подобного представления был известный американский исследователь У. Хартманн (W. K. Hartmann), мы будем обозначать число кратеров в интервалах с постоянным D₂/D₁ = ?2 как N_H:

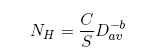
(заметим, что сам Хартманн иногда использовал не средний диаметр D_av, а меньший диаметр интервала измерений D₁; интересующийся читатель должен быть настороже).

Для представления инкрементальных данных рекомендуется использовать линейку граничных диаметров интервалов, один из которых фиксирован при D = 1 км. Тогда интервалы диаметров в сторону больших размеров составляют 1,41, 2, 2,83, 4 км и т. д., а в сторону меньших размеров — 707, 500, 353, 250 м и т. д., при стандартном отношении D₂/D₁ = ?2.

R-представление. Кумулятивное и инкрементальное представления данных для интервалов диаметров кратеров более одного порядка величины вызывают трудности при графическом представлении — диапазон значений величины N изменяется на три порядка (при b— 3) при изменении D на порядок величины. Поэтому для графического представления данных рабочая группа НАСА [Arvidson et al., 1979] стандартизировала так называемое R-представление (от англ. Relative — относительный). При этом круто падающая зависимость N(H) представляется не в абсолютных значениях, а нормируется относительно базовой степенной функции, за которую принята функция D^-3. Таким образом, R-представление изображает отклонение распределения по размерам от простой круто падающей степенной функции:

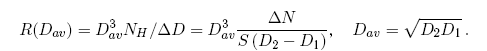
Согласно стандартной модели, статистическая ошибка подсчета числа кратеров N в заданном интервале диаметров оценивается как ±?N. Этот интервал обычно обозначается на рисунках отрезком вертикальной линии. Для R-представления ошибка представляется как интервал от R(N + ?N) до R(N — ?N). После формальных (но необходимых) объяснений терминологии можно перейти к описанию собственно наблюдательных данных о распределении лунных кратеров по размерам. При этом нужно принимать во внимание два важных обстоятельства: 1) уничтожение части кратеров планетарными геологическими процессами; 2) достижение предельной (равновесной, насыщенной) плотности кратеров, определяемой как отношение их числа к площади изучаемой поверхности. Стирание кратеров вулканизмом было характерно для Луны в течение первых 2,5 млрд лет ее истории [Hiesinger et al., 2003; Hiesinger et al., 2000]. В последние 2 млрд лет ландшафт Луны изменялся в основном за счет образования новых ударных кратеров. Однако на Земле и Марсе наличие атмосферы и гидросферы делает уничтожение кратеров важным конкурентом процесса их образования. Здесь наблюдаемое число кратеров ниже некоторого характерного размера остается постоянным за счет равенства скоростей образования новых и стирания старых кратеров. Поэтому необходимо различать статистику подсчитанных кратеров и статистику общего количества кратерообразующих ударов. В идеальной ситуации некий геологический процесс полностью обновляет участок поверхности, на котором начинают стохастически накапливаться новые ударные кратеры. В этом случае наблюдатель фиксирует все кратеры (и их размеры), а статистика распределения кратеров по размерам соответствует (с учетом определенных законов подобия) статистике распределения по размерам малых тел Солнечной системы. В таких условиях полученное распределение по размерам называют производящей функцией.

Второе из двух отмеченных выше усложняющих обстоятельств состоит в том, что по мере накопления со временем все большего количества кратеров они начнут накладываться друг на друга, разрушая ранее образованные кратеры. Ясно, что в этом случае число наблюдаемых кратеров различных размеров будет меньше, чем число ударов. Такие поверхности называются насыщенными или равновесными по отношению к образованию новых кратеров. Для достаточно широкого класса распределений по размерам падающих тел (оно должно быть достаточно крутым с b > 2) равновесная популяция кратеров будет иметь показатель степени в законе распределения по размерам b ? 2 [Gault, 1970]. Поверхности, насыщенные кратерами, были экспериментально обнаружены на снимках Луны высокого разрешения [Shoemaker et al., 1970]. Позднее особенности достижения равновесия кратерных популяций были изучены теоретически и экспериментально [Hartmann, 1984; Hartmann and Gaskell, 1997; Woronow, 1977].

С учетом усложнений, которые обсуждались выше, для начального представления статистики лунных кратеров удобно следовать логике Хартманна, который избрал процессом, достаточно быстро обновившим большие участки лунной поверхности, излияние морских базальтов на видимой стороне Луны. Согласно имеющимся данным, базальты излились на поверхность довольно быстро (в геологическом смысле) — в интервале времени от 3,5 до 2,8 млрд лет назад образовалось почти 60 % общей площади лунных базальтовых морей [Иванов, 2005a; Hiesinger et al., 2003; Hiesinger et al., 2000; Shoemaker and Wolfe, 1982]. Распределение по размером кратеров, наложенных на поверхность лунных морей, показано на рис. 9.1 в инкрементальном виде (а) и в R-представлении (б). Для удобства использования эти данные можно выразить в аналитическом виде как зависимости числа N_H кратеров на 1 км² площади в интервалах диаметров с отношением D₂/D₁ = ?2 в виде [Hartmann, 2005; Ivanov et al., 2001]:

lgN_H = ?2,61 ? 3,82 lgD_L, 0, 3 <D_L < 1,41 км, (9.1)

lgN_H = ?2,920 ? 1,80 lgD_L, 1,41 <D_L < 64 км, (9.2)

lgN_H = ?2,198 ? 2,20 lgD_L, D_L > 64 км, (9.3)

где для определения интервала диаметров использовано левое (меньшее) значение граничного диаметра D_L.

Для кратеров менее 300 м в диаметре для получения производящей функции нужно использовать более молодые участки поверхности, еще не успевшие насытиться постоянно образующимися новыми кратерами. Обычно на Луне такие участки находятся на покровах выбросов и днищах больших кратеров. При использовании этих данных производящее распределение по размерам можно продлить для диаметров < 300 м. Чтобы формально это продолжение соответствовало распределению на лунных морях, его можно записать в виде

lgN_H = ?2,0 ? 2,90 lgD_L, 0,01 < D_L < 0,125 км. (9.4)

С таким добавлением кривая N(D) может двигаться вверх и вниз вдоль вертикальной оси для более молодых и более древних участков лунной поверхности.

Как видно из рис. 9.1, в диапазоне от метровых до километровых кратеров зависимость числа кратеров от их диаметра имеет сложную форму, лишь кусочно соответствующую простым степенным соотношениям.

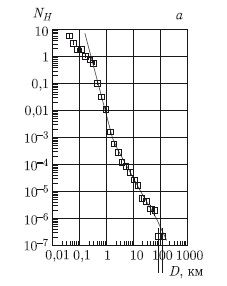
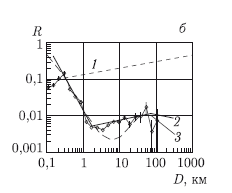
^{Рис. 9.1. Распределение по размерам кратеров на поверхности лунных базальтовых морей в инкрементальном виде (а) и в R-представлении (б). Штриховая прямая 1 на рисунке б показывает примерный уровень «эмпирического» насыщения поверхности кратерами [Hartmann, 1984]. Рисунок первоначально был опубликован автором в работе [Neukum et al., 2001], позднее опубликован в русском варианте [Иванов, 2005a]. Сегменты степенных зависимостей (прямые участки на линии 2) соответствуют формулам (9.1) — (9.3). На рисунке б показана также штриховая линия 3, соответствующая аналитической кривой Нойкума [Ivanov, 2001; Neukum et al., 2001]}

Возраст поверхности, на которой накопились эти кратеры, можно в среднем считать равным 3,3–3,4 млрд лет. Чтобы описать накопление кратеров со временем, или, наоборот, по известному количеству кратеров оценить возраст поверхности, применяется следующий прием: в каком бы диапазоне диаметров ни были произведены измерения, через измеренные точки проводится кривая, соответствующая производящей функции (показанной на рис. 9.1) и находится значение, на котором пересекается вертикальная линия, соответствующая D = 1 км (даже если истинное число кратеров с D? 1 км находится в зоне насыщения). Это значение N(D > 1 км) в кумулятивном представлении или соответствующее ему значение N_H(D_L = 1 км) позволяют ввести временну?ю шкалу, показывающую, с какой скоростью накапливаются кратеры. Такая шкала была построена с помощью измерения радиологического возраста образцов, доставленных с Луны КА «Аполлон» и автоматическими станциями серии «Луна». Параллельно по снимкам высокого разрешения измерялось распределение по размерам кратеров вокруг точек отбора образцов. С помощью стандартного (производящего) распределения по размерам все измерения были приведены к значению N(D > 1 км), которое сравнивается со значениями радиологического возраста образцов. Если поток кратерообразующих тел постоянен, значение N(D > 1 км) должно линейно расти с увеличением возраста пород. На рис. 9.2 показаны результаты такой обработки данных. Данные по возрасту кратера Коперник признаются весьма сомнительными — на лунной поверхности был собран материал, лежащий в пределах яркого луча, исходящего из кратера. Однако выживание вещества на поверхности Луны в течение 1 млрд лет является маловероятным из-за потока микрометеоров [Stoffler et al., 2006].

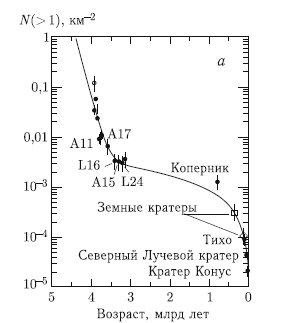
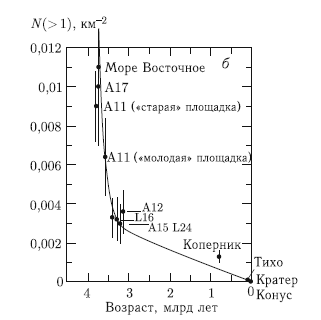
^{Рис. 9.2. Накопленное количество кратеров на различных участках лунной поверхности в зависимости от ее возраста, определенного по возвращенным лунным образцам: а) логарифмический масштаб по оси ординат, б) линейный масштаб по оси ординат.}

^{Сплошная кривая — аналитическое представление [Stoffler et al., 2006]}

На рис. 9.2. видны следующие особенности, важные для анализа АКО (Луна и Земля находятся в едином потоке бомбардирующих тел): в течение последних 3 млрд лет поток кратерообразующих тел был примерно постоянным; ? 4 млрд лет назад поток кратерообразующих тел был в 100–500 раз выше современного. Потоки в течение первых 0,5 млрд лет (не оставившие известных кратерных записей) являются в настоящее время предметом активных исследований [Hartmann et al., 2002]. К настоящему времени показано, что первоначальная идея о постепенном уменьшении темпа бомбардировки, начиная со стадии аккумуляции планет, не выдерживает проверки [Bottke et al., 2007a]. Причины резкой активизации бомбардировки примерно 4 млрд лет назад не ясны. Предложена интересная гипотеза (так называемая модель Ниццы — по названию города, где в обсерватории местного университета работают основные авторы модели). Согласно этой модели, миграция орбит планет-гигантов привела примерно 4 млрд лет назад к попаданию в резонанс периодов обращения Юпитера и Сатурна вокруг Солнца. Резонансные явления «встряхнули» всю Солнечную систему, вызвав поток «новых» кратерообразующих тел. Затухание этого потока и наблюдается на временно?м ходе кривой N(D) [Gomes et al., 2005; Tsiganis et al., 2005].

Несмотря на относительно низкую точность данных, показанных на рис. 9.2, Нойкум [Neukum, 1983; Neukum et al., 2001] предложил часто используемое аналитическое выражение для изменения параметра N(> 1 км) от времени накопления кратеров T (в данном случае N измеряется как число кратеров диаметром более 1 км на площади 1 км², а время — в млрд лет):

N(> 1 км) = 5,44 10^-14[exp(6,93T) — 1] + 8,38 10^-4 Т. (9.5)

Сплошные кривые на рис. 9.2 построены именно по этому уравнению.

Проверка общей картины для последних 100 млн лет может быть проведена по данным о малых (D < 100 м) кратерах Луны. Сравнивая их с современным потоком метеороидов на границе земной атмосферы [Brown et al., 2002; Halliday et al., 1996], можно проверить постоянство потока малых тел метровых размеров [Ivanov, 2006]. На рис. 9.3 показаны данные измерения распределения по размерам на наиболее молодых датированных участках лунной поверхности. Эти данные показывают, что немногочисленные точки измерений позволяют предположить (пока не доказано обратное), что поток кратерообразующих тел был примерно постоянен в последние 100 млн лет. Более того, этот поток примерно соответствует современному потоку болидов, фиксируемых в земной атмосфере [Ivanov, 2006].

Примерное постоянство потока малых тел на Землю и Луну при времени усреднения 0,1–1 млрд лет не означает, конечно, что не существует кратковременных (? 100 млн лет) вариаций потока.

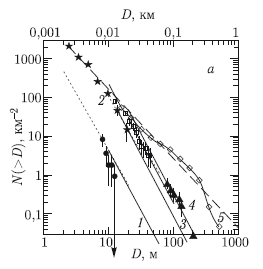
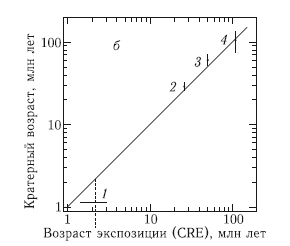
^{Рис. 9.3. а) Кумулятивные зависимости N(> D) для малых (D < 100 м) кратеров, наложенных на покровы выбросов 4 лунных кратеров, возраст которых был определен по длительности экспозиции в потоке космических лучей (cosmic ray exposure = CRE) для возвращенных на Землю образцов: 1 — кратер Южный Лучевой; 2 — кратер Конус; 3 — кратер Северный Лучевой [Moore et al., 1980]; 4 — кратер Тихо [Koenig et al., 1977]. Для сравнения показаны данные для лунных морей, иллюстрирующие в данном случае положение кривой насыщения 5. Пунктирная линия показывает средний уровень N(D) для насыщенной кратерами поверхности N(> D) = 0,047D-1,83 [Hartmann, 1984], хорошо соответствующий самым маленьким из измеренных кратеров на площадке у кратера Конус. б) Cравнение возраста площадок измерений по хронологии Нойкума [Neukum et al., 2001] для кратеров с D > 10 м и зависимости N(> D) ? D-2,9 для меньших кратеров. Возраст космической экспозиции (CRE) определен в работах [Arvidson et al., 1975; Drozd et al., 1974]}

В потоке микроскопических метеоров, например, известны спорадическая и потоковые составляющие. В диапазоне размеров тел, представляющих интерес с точки зрения АКО, механизмом вариации потока может быть, например, разрушение астероида Главного пояса при условии близости его орбиты (в фазовом пространстве) к той или иной резонансной зоне. Резонансное влияние планет-гигантов на астероиды приводит к быстрому изменению их орбит, обновляя поток тел на орбитах, пересекающих орбиты планет. Начало огромному циклу работ по эволюции орбит астероидов на столкновительные орбиты положила, в частности, работа [Farinella et al., 1994]. К настоящему времени показаны возможности эффективного пополнения популяции малых тел на столкновительных орбитах [Gladman et al., 2000]. В то же время эти исследования показали, что малые тела удерживаются на околоземных орбитах всего 3–30 млн лет [Gladman et al., 1997]. Этот масштаб времени и задает примерный интервал усреднения, при котором можно говорить о постоянстве бомбардирующего потока.

В недавней работе [Bottke et al., 2007b] показано, что всплеск частоты падений 60–100 млн лет назад мог быть вызван разрушением в Главном поясе астероида, фрагменты которого в настоящее время образуют семейство Баптистины. В этом случае и кратер Чиксулуб на Земле (возраст 65 млн лет), и уже упоминавшийся кратер Тихо на Луне (возраст 100 млн лет) образовались в период повышения потока бомбардирующих тел из новообразованного семейства. Однако увеличение диапазона усреднения до, например, 500 млн лет нивелирует такой всплеск, который не может длиться более 150–200 млн лет [Bottke et al., 2007b].

Статистика лунных кратеров в применении к Земле. На Земле к настоящему времени известно около 180 кратеров, примерно для 160 из которых уверенно доказано происхождение в результате высокоскоростного удара. На первый взгляд кажется, что при известном времени образования данные для 160 структур представляют собой хорошую базу данных для оценки частоты столкновений крупных космических тел с Землей. Однако важные обстоятельства затрудняют простую интерпретацию имеющихся данных. Во-первых, далеко не для всех кратеров известно точное время образования — если не найден ударный расплав, для которого возможно определение изотопного возраста кристаллизации, то в распоряжении геологов остаются только приблизительные стратиграфические методы. Во-вторых, эндогенная активность Земли велика по сравнению с Луной, и кратеры диаметром менее 20–30 км уже не дают полной записи ударных событий. В-третьих, две трети поверхности Земли покрыты океанами, существующими за счет субдукции плит. Обновление дна океана происходит так быстро, что его возраст составляет в среднем ? 50 млн лет и лишь малая его площадь достигает возраста 120 млн лет. Поэтому кратеры больших размеров на дне океана разрушаются тектоникой плит. Малые кратеры образуются в малом количестве за счет защитного слоя океанской воды.

Для сравнения, геологический возраст наиболее стабильных участков континентальной коры достигает 2 млрд лет. Там и находится основное количество известных метеоритных кратеров. Возраст наиболее крупных из них (диаметр до эрозии ? 200 км [Иванов, 2005b]) близок к 2 млрд лет.

По этим причинам информация о частоте столкновений космических тел с Землей может быть извлечена из данных о земных кратерах только путем совместного использования с данными по лунным кратерам. Для пересчета частоты образования кратеров на Луне к условиям Земли необходимо знать распределение тел по скоростям сближения (от этого зависит эффективность гравитационной фокусировки) и законы подобия при образовании ударных кратеров (чтобы учесть разницу в силе тяжести на поверхности Луны и Земли). Методика такого пересчета от Луны к Земле (а также к другим планетам) была подробно изложена [Hartmann, 1977; Ivanov, 2001; Neukum and Ivanov, 1994]. Приведем здесь главные результаты.

Скорость сближения малых тел с Землей определяется заселенностью различных орбит. Ее статистика может быть получена с помощью моделирования телескопических наблюдений малых тел [Bottke et al., 2002b; Stuart and Binzel, 2004] или с помощью таблиц оскулирующих элементов орбит известных околоземных астероидов [Ivanov, 2001; Ivanov and Hartmann, 2007]. Отличаясь в деталях, оба метода дают схожие результаты.

Для наблюдаемой сейчас совокупности астероидов размером более 1 км, пересекающих орбиту Земли, среднее количество столкновений составляет примерно 3,5 ± 0,5 за 1 млрд лет. Это означает, что если число тел заданного размера составляет 1000 (что близко к оценке числа астероидов с абсолютной звездной величиной H < 18 [Stuart and Binzel, 2004]), то в среднем интервал между столкновениями составляет около 3,5 млн лет, что сравнимо с временем жизни тел на околоземных орбитах [Gladman et al., 2000]. Значит, лишь единицы из известной сегодня тысячи тел реально столкнутся с Землей, а большинство будет выброшено за орбиту Юпитера или упадет на Солнце. Новые тела из пояса астероидов придут им на смену.

Расчет вероятности столкновений автоматически приводит к оценке вероятной скорости удара. На рис. 9.4 показаны распределения по скоростям астероидов, сталкивающихся с Землей и Луной. Модель Боттке [Bottke et al., 2002] дает несколько большие значения средних скоростей удара за счет ненаблюдаемых тел на орбитах с высоким наклонением. Тем не менее, все модели сходятся в том, что средние скорости удара на Земле и Луне близки и составляют 18–20 км/с.

Эти же оценки вероятности столкновений приводят к вычислению отношения числа ударов по Земле и Луне тел одного размера на единицу площади поверхности. Это отношение (иногда называемое болидным отношением, R_b) составляет 1,6–1,8. Как видно, в дополнение к 13-кратному отношению площадей поверхности (6370/1738)² Земля притягивает примерно в 1,7 раза больше тел. В сумме получается, что на один удар по Луне приходится около 20 ударов по Земле (для тел одного и того же размера). Но размеры кратеров, образуемых на Луне, будут несколько больше, чем на Земле, из-за меньшей силы тяжести.

Для представления основных закономерностей подобия при образовании ударных кратеров можно представить простую зависимость отношения диаметра кратера к диаметру ударника для лунных условий при средней скорости удара 20 км/с (рис. 9.5).

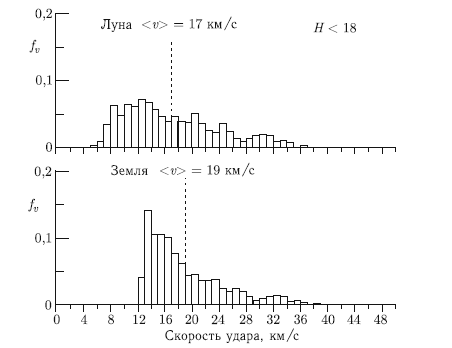
^{Рис. 9.4. Частота скоростей ударов наблюдаемых малых тел по Луне и Земле. По вертикальной оси отложены доли ударов в указанных на горизонтальной оси интервалах скоростей шириной 1 км/с (полное число ударов равно 1)}

С точки зрения свойств материала мишени различаются два основных случая — пористая мишень (типа сухого песка или лунного реголита) и мишень из сплошной (малопористой) горной породы. Для пористой породы при диаметре кратера 300 м ударник должен быть в 30 раз меньше диаметра кратера — примерно 10 м. При падении на поверхность малопористых пород относительный размер кратера будет больше (из-за отсутствия потерь на нагрев динамически сжимаемой пористой среды) — примерно в 4/3 раза. Но зато малопористые породы имеют большую прочность, что приводит к пересечению кривых для малопористых и пористых пород в диапазоне диаметров кратеров около 1 м. При диаметре кратеров 100 м и более размеры кратера ограничиваются не столько прочностью пород, сколько затратами энергии на подъем выбрасываемых пород в поле тяжести. Такие кратеры называются «гравитационными». При диаметре кратера порядка 100 км для его образования требуется ударник всего в 10 раз меньший диаметра кратера. При этом возникает дополнительное новое явление — гравитационный коллапс кратеров, приводящий к образованию центральных одиночных и кольцевых горок, причем происходит уширение кратера за счет оползания его бортов.

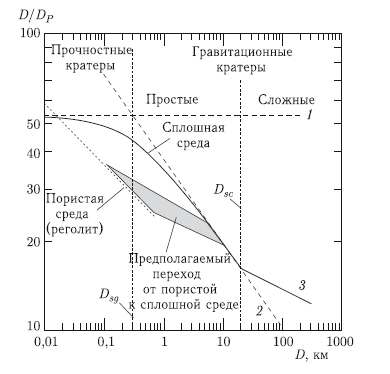
^{Рис. 9.5. Зависимость отношения диаметра лунного ударного кратера к диаметру каменного астероида D/D_P от диаметра кратера D при скорости удара 18 км/с. Граничный диаметр кратеров D_sg (strength-to-gravity) отмечает диапазон перехода от доминирования прочности к доминированию силы тяжести в определении конечного размера кратера. Граничный диаметр D_sc (simple-to-complex) отмечает переход от простых чашеобразных кратеров к сложным кратерам с центральной горкой (подробнее см. [Ivanov and Hartmann, 2007])}

В земных условиях вся эта картина сдвигается в сторону меньших диаметров из-за большей силы тяжести на Земле. Для кратеров диаметром & 10 км численное моделирование процесса кратерообразования в сочетании с данными геолого-геофизических исследований позволяет дать простую приближенную оценку связи параметров ударника и диаметра возникающего при ударе кратера [Ivanov and Hartmann, 2007]:

D ? 4(D_P v^0,58)^0,91, (9.6)

где диаметр кратера D и диаметр каменного астероида D_P выражены в км, а скорость удара v — в км/с. Как ни странно, такая простая формула вполне прилично выполняется для кратеров диаметром от ? 5 до 200 км. Для кратеров меньшего размера большую роль играет строение и свойства массива горных пород в точке удара.

Используя все вышеперечисленные модели, можно пересчитать лунный темп кратерообразования к земным условиям и оценить среднюю частоту образования земных метеоритных кратеров, основываясь только на лунной кратерной хронологии, показанной на рис. 9.2. Для простоты мы не будем делать поправок на влияние атмосферы (что представляет особую задачу — см., например, [Bland and Artemieva, 2003; Bland and Artemieva, 2006]). Наши оценки — это оценки числа столкновений малых тел с Землей, энергия которых выражается в виде диаметра эквивалентного кратера, который мог бы образоваться на поверхности гипотетической безатмоферной Земли. На рис. 9.6 показаны лунные изохроны — кумулятивные оценки числа ударов по всей поверхности Земли, энергия которых выражена в диаметре эквивалентного кратера без учета атмосферы. Для кратеров размером более нескольких километров эти оценки соответствуют реальным кратерам. Такое построение удобно использовать для оценок частоты ударов по Земле.

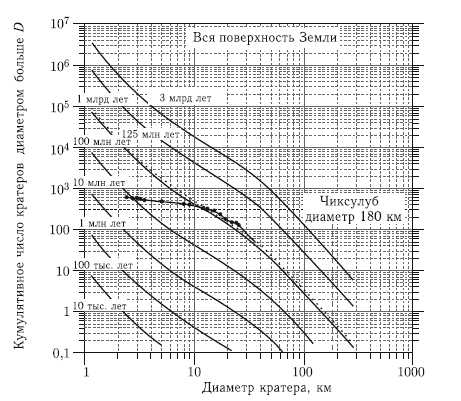
^{Рис. 9.6. Кумулятивное число ударных кратеров на всей поверхности Земли, образовавшихся за данный промежуток времени, оцененное путем пересчета лунной кратерной хронологии. Черными точками показаны независимые оценки, сделанные методом «ближайшего соседа» по сохранившимся ударным кратерам на суше [Hughes, 2000], пересчитанные к полной площади поверхности Земли}

Проверку модели переноса лунной кратерной хронологии на Землю сделать непросто, так как в земных условиях трудно оценить площадь поверхности, на которую нужно нормировать число обнаруженных ударных кратеров [Grieve, 1984; Grieve and Shoemaker, 1994]. Однако в работе [Hughes, 2000] была сделана оценка числа кратеров на единицу площади методом «ближайшего соседа», не требующая сложного анализа геологической ситуации. Для представительной выборки кратеров моложе 125 млн лет автор построил кумулятивное распределение по размерам, показанное на рис. 9.6 пунктирной линией. Можно только удивляться очень хорошему соответствию этих данных модельным результатам переноса лунной кратерной хронологии. Тем не менее, такое совпадение (наряду с обсуждавшимся выше совпадением современного потока болидов и темпа образования малых кратеров на Луне в последние 100 млн лет) позволяет отнестись к полученным результатам с определенным доверием, однако с продолжением совершенствования методик оценки астероидной опасности в будущем.

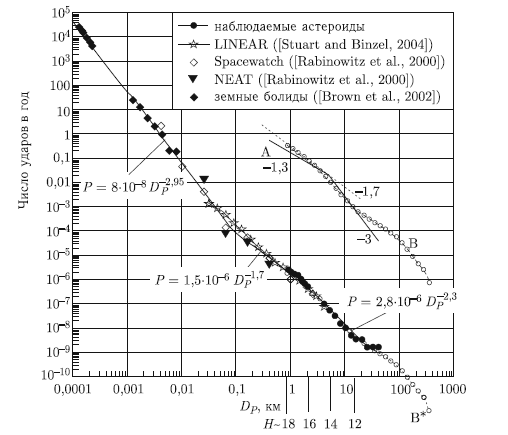
^{Рис. 9.7. Сравнение вероятностей столкновения с Землей астероидов, сделанное по хронологии лунных ударных кратеров в сравнении с данными по болидам [Brown et al., 2002; Halliday et al., 1996] и по моделированию астрономических наблюдений малых тел [Rabinowitz et al., 2000; Stuart, 2001; Stuart and Binzel, 2004]. Для сравнения показаны оценки распределения по размерам астероидов в Главном поясе по данным [Ivezic et al., 2001] (А) и [Jedicke et al., 2002] (B). Кривая B* представляет собой кривую B, масштабируемую к количеству околоземных астероидов}

Показанные на рис. 9.6 распределения кратеров по размеру можно перевести в оценки частоты падения на Землю тел различного диаметра (или непосредственно в кинетическую энергию ударных событий). На рис. 9.7 показаны разнородные данные, полученные в различных диапазонах размеров малых тел различными методами — по наблюдению болидов, по подсчету лунных кратеров, по моделированию астрономических наблюдений малых тел вблизи Земли и в Главном поясе астероидов. Имея каждый в отдельности большую степень неопределенности, все вместе они позволяют построить общую картину частоты падения тел (или, что то же, распределения тел по размерам), бомбардирующих Землю в текущую эпоху. Вырисовывается довольно сложная картина наложения нескольких простых степенных законов, каждый из которых, однако, не может быть экстраполирован за пределы своего диапазона.

Следуя традициям исследователей лунных кратеров, мы можем в предварительном порядке предложить кусочно-линейную (в логарифмических координатах) зависимость частоты ударов от размера падающих тел. С многочисленными оговорками о точности моделей и данных наблюдений мы предлагаем оценивать вероятность входа в атмосферу тел c диаметром > D_P при номинальной плотности ударников 2700 кг/м³ [Stuart and Binzel, 2004] следующими соотношениями [Ivanov and Hartmann, 2007]:

P(> DP) ? 8 · 10^?8D_P^?2,95, D_P < 100 м; (9.7)

P(> DP) ? 1,5 · 10?6D_P^?1,7, 100 м < D_P < 1 км; (9.8)

P(> DP) ? 2,8 · 10?6D_P^?2,3, 1 км < D_P < 20 км. (9.9)

Данный текст является ознакомительным фрагментом.