VI. ТЕОРИЯ ЭПИЦИКЛИЧЕСКИХ ДВИЖЕНИЙ

VI. ТЕОРИЯ ЭПИЦИКЛИЧЕСКИХ ДВИЖЕНИЙ

Теория гак называемых вторичных кругов или эпициклов обыкновенно приписывается Клавдию Птолемею (70—147 гг. хр. эры), хотя этот тщательный наблюдатель и вдумчивый мыслитель не является ее основателем. Зачатки этой теории, т. е. мысль, что движения небесных тел могут быть представлены комбинацией однообразных круговых движений, не были чужды Гиппарху. Из слов самого Птолемея видно, что еще до Гиппарха знаменитый математик Аполлоний Пергский (250–205 гг. до хр. эры) прибегал к способу эпициклов для объяснения второго неравенства, т. е. стояний и попятного движения планет. Но хотя Птолемей не является творцом метода эпициклов, он глубоко и обстоятельно разработал этот способ. Мысль Гиппарха о создании астрономической системы, объясняющей движения всех небесных тел, нашла в его лице весьма последовательного сторонника. Поэтому та картина мира, которую отстаивал Птолемей, называется птолемеевой системой мира, несмотря на то, что она постепенно создавалась мыслителями греческого мира.

Фиг. 13. Клавдий Птолемей (как он чаще всего изображается).

Цель птолемеевой системы — дать возможность вычислить положения небесных тел на небесной сфере для любого момента. В общем эта система представляет собой чрезвычайно остроумную и математически изящную теорию запутанного видимого движения планет, основанную на приеме сложения двух или более круговых движений.

Сущность этой теории состоит в следующем. Все планеты равномерно движутся по особым кругам, названным эпициклами. Центр каждого эпицикла в то же время скользит также с постоянной скоростью по окружности другого, гораздо большего круга, названного деферентом (кругом «управляющим», уносящим). При этом Птолемей допускал, что Земля не находится в геометрическом центре деферента, а лишь около него, так что деферент является эксцентрическим кругом, причем движение по деферентам и эпициклам происходит с запада на восток с постоянной скоростью, равномерно. Значит каждая планета как бы насажена на обод вращающегося колеса, центр которого в свою очередь обращается вокруг Земли, но только медленнее.

Простые эпициклы все же оказались недостаточными для объяснения всех особенностей (аномалий, неравенств) планетных путей, и Птолемей был вынужден придумать с этой целью крайне сложные схемы. Поэтому он сам заметил: «Легче, кажется, двигать самые планеты, чем постичь их сложное движение».

Эта сложность в конце концов явилась причиной падения системы Птолемея. Птолемей, как и все величайшие астрономы древности, не мог освободиться от укрепившихся идей Аристотеля о божественности, совершенстве и вечности небесных тел и их движений. Как мы потом увидим, даже Коперник продолжал держаться мнения, что планетные орбиты могут быть лишь круговыми, вследствие чего ему не удалось окончательно отказаться от эпициклов, полностью опровергнуть положения Птолемея. Это удались только ярому коперниканцу Кеплеру, показавшему на основании наблюдений Тихо Браге, что планеты движутся не по круговым, а по эллиптическим орбитам.

Птолемей изложил астрономические (и вместе с тем тригонометрические) знания своего времени, значительно умножив и расширив их, в сочинении, которое по — гречески называлось «Мегалэ синтаксис» («Большое сочинение»). Оно сохранилось под искаженным арабским названием «Альмагест», потому что вначале оно стало известно лишь по переводу с арабского языка. В этом же большом сводном труде, пользовавшемся в ученых кругах огромным авторитетом вплоть до времен Галилея и Кеплера, он подробно развил свою систему мира, сыгравшую исключительную роль в истории астрономии.

В основе этой системы мира лежит аристотелева физика: шарообразная Земля стоит неподвижно в центре вселенной, а вселенная пространственно ограничена, замыкается небесной сферой, которая вместе с находящимися на ней неподвижными звездами совершает суточное вращение. Между Землей и небом нет ничего общего, и поэтому, — говорил Птолемей, — «не должно сравнивать небесных тел с телами земными и судить о причинах, действующих на первые, по телам, с ними вовсе разнородными». Птолемей подчеркивал, что те, которые с трудом допускают, чтобы такое тяжелое тело, как Земля, могло держаться свободно и никуда не упасть, забывают что все падающие тела стремятся перпендикулярно к поверхности Земли и к ее центру или, что одно и то же, к центру вселенной. Но подобно тому как свободно падающие тела имеют стремление к центру мира, и Земля имела бы то же стремление, если бы она была сдвинута с этого центра.

Согласно системе Птолемея, вокруг покоящейся в центре вселенной Земли обращаются по порядку: Луна, Меркурий, Венера, Солнце, Марс, Юпитер и Сатурн. Птолемей указывал, что такой порядок приняли еще «древние математики», и что трудно окончательно решить, правилен ли такой порядок расположения светил вокруг Земли или нет. Он, правда, пытался дать объяснение такого расположения светил, но при этом не касался величины радиусов этих орбит, не приводил расстояний упомянутых небесных тел от Земли, так как, повидимому, не смог определить, во сколько раз, например, Сатурн дальше от Земли, чем Меркурий.

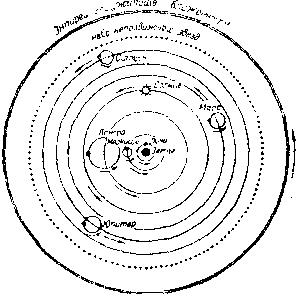
Фиг. 14. Птолемеевская система мира с главными эпициклами, по которым движутся планеты. Средневековые богословы за небом неподвижных звезд помещали эмпирей или «жилище блаженных» — местопребывание бога, ангелов и прочих «небожителей».

Он исходил из предположения, что чем медленнее движения планеты, тем дальше она от Земли, так что Луна должна находиться ближе всех к нам, а Сатурн — дальше всех. Что касается Солнца, то оно должно быть дальше от Земли, чем Луна, потому что движение его медленнее и Луна часто покрывает собой Солнце, вызывая этим солнечные затмения. Орбиты Меркурия и Венеры Птолемей принял внутри солнечной орбиты, орбиты же Марса, Юпитера и Сатурна — вне солнечной орбиты, потому что первые две планеты всегда видны близ Солнца, а другие удаляются от Солнца на большие расстояния. Подобное распределение планет он оправдывал еще тем, что всего «приличнее» принимать столько же небесных тел над Солнцем (Марс, Юпитер и Сатурн), сколько и под ним (Луна, Меркурий и Венера).

Как мы уже отметили, теория эпициклов, исходя из допущения равномерно — кругового движения небесных тел, стремится прежде всего объяснить особенности в движении планет. Она обращает внимание на то, что при движении по эпициклу и центра эпицикла по деференту, направление движения планеты должно меняться. В этих переменах она и видит объяснение всех кажущихся неправильностей в движении планет.

Когда движение планеты по эпициклу направлено в сторону движения центра эпицикла по деференту, наблюдателю с Земли должно казаться, что планета движется со скоростью равной сумме этих скоростей, так что в это время должно получиться прямое движение планеты. Наоборот, когда движения эпицикла и планеты направлены в прямо противоположные стороны, причем движение планеты по эпициклу быстрее движения центра эпицикла, наблюдателю с Земли должно казаться, что планета движется со скоростью, равной разности этих скоростей, и поэтому в это время планета будет казаться движущейся в обратном направлении. Наконец, в тех точках, где планета меняет направление своего движения, и скорость движения по эпициклу делается равной скорости движения центра эпицикла по деференту, планета с Земли должна некоторое время казаться остановившейся. После стояния планеты, видимая с Земли скорость ее движения по эпициклу превосходит скорость движения центра эпицикла, причем оба эти движения направлены в разные стороны, и наблюдателю с Земли кажется, что прямое движение планеты изменилось на обратное и что планета «завязала узел», описала петлю среди звезд.

Мы видим, таким образом, что при помощи теории эпициклов и деферентов удается объяснить второе неравенство в движении планет, т. е. прямые и попятные движения планет и их стояние. Но интересно, что одновременно представить правильно и направления с Земли планеты и расстояния планет от Земли одними и теми же эпициклами нельзя.

Чтобы положения планет, вычисленные на основании теории эпициклов, согласовались с наблюдаемыми положениями, необходимо было знать радиусы эпициклов и деферентов и скорости движения. С этой целью Пто- лемей принял, что в периодах времени обращения по этим кругам есть различие для трех «верхних», т. е. далеких планет (Марса, Юпитера и Сатурна) и для двух «нижних», т. е. близких (Меркурия и Венеры). Все верхние планеты совершают полный оборот по окружности эпицикла в одинаковый промежуток времени, равный году, т. е. периоду, в течение которого Солнце возвращается к одним и тем же звездам. Наоборот, у нижних планет период обращения по эпициклу различен и равен промежутку времени, в течение которого планета возвращается к прежним зоездам (Меркурий—88 дней, Венера — 225). Точно так же Птолемей определял различно промежуток времени, в течение которого центр эпицикла совершает полный оборот по окружности деферента. Он допускал, что для Марса, Юпитера и Сатурна этот промежуток различен и равен тем периодом времени, в течение которого каждая из этих планет, описав полную окружность на небосводе, возвращается к прежним звездам (Марс — почти 2 года, Юпитер—12 лет, Сатурн — почти 30 лет). Что же касается других двух планет, Меркурия и Венеры, которые видны лишь недалеко от Солнца, то для них, наоборот, этот промежуток Птолемей считал одинаковым и равным году.

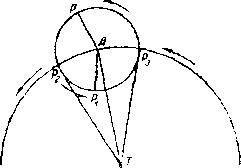
Фиг. 15. Видимое движение планеты по Птолемею. А — центр эпицикла, по которому равномерно движется планета в том же направлении, что и деферент, движущийся вокруг земли Т. Когда планета находится в точке Р, ее движение с Земли будет казаться прямым, ибо движения по эпициклу и деференту направлены в одну сторону. При положении Pj движение планеты из точки Т будет казаться обратным, ибо движение по эпициклу направлено в обратную сторону. При переходе от одного движения к другому, в точках Р_? и Р, планета будет казаться остановившейся.

По системе Птолемея Земля занимает несколько эксцентрическое положение внутри деферента, а все плоскости деферентов проходят через центр земного шара и наклонены друг к другу под различными углами, равно как н плоскости эпициклов к соответствующим деферентам. Дело в том, что наблюдения какой?нибудь планеты, например Юпитера, показывают, что эта планета не движется в плоскости эклиптики (т. е. того круга, по которому, нам кажется, движется Солнце), а бывает то к северу, то к югу от этого круга. Чтобы учесть это обстоятельство, Птолемей принял, что плоскости тех кругов, которые служат для объяснения видимого движения Юпитера и других планет, не совпадают с плоскостью круговой орбиты Солнца, а несколько наклонены к ней. Следовательно, чтобы на основании теории эпициклов воспроизвести движение какой- нибудь планеты со всеми ее петлями, надо не только подобрать соответствующим образом скорости движения планеты и центра эпицикла (т. е. радиусы деферента и эпицикла и времена обращения центра эпицикла по деференту и планеты по эпициклу), но и углы наклона плоскостей деферента и эпицикла к эклиптике.

Итак, в движении планет были замечены некоторые особенности, для объяснения которых Птолемею приходилось плоскость каждого эпицикла наклонять под различными углами как к плоскостям остальных эпициклов, так и к плоскости деферента. Таким образом получилась весьма сложная система взаимно наклоненных круто в. А если мы к тому же примем во внимание, что вследствие крайней сложности закона изменения скорости видимого движения планет, для каждой из планет пришлось ввести целый ряд эпициклов, то станет ясно, какой громоздкой и запутанной была птолемеева система мира.

Особенно важно то, что где одного эпицикла для объяснения движения небесного тела нехватало, там Птолемей считал возможным ввести целую комбинацию эпициклов. В этом случае центр первого эпицикла каждой планеты движется по деференту, но по окружности первого эпицикла движется уже не планета, а лишь центр второго эпицикла и т. д. Сама планета, двигаясь по одному из последних эпициклов, должна совершать в высшей степени сложное движение вокруг Земли. Можно даже сказать, что самое движение по кругам в сущности уничтожено теорией Птолемея, так как согласно этой теории, планеты должны были описывать винтовые линии, так называемые эпициклоиды. Движение по такой кривой, происходящее даже от одновременного движения лишь по двум кругам, столь же мало заслуживает названия кругового движения, как и движение тел по параболе не может быть названо прямолинейным, хотя и слагается из движений по двум прямым линиям.

По теории Птолемея кажущиеся движения планет совершенно не зависят от размеров эпицикла и деферента, лишь бы они изменялись пропорционально. Поэтому этот астроном не давал числовых величин радиусов этих кругов, а лишь ограничивался отношением между этими радиусами, не интересуясь вопросом об изменениях расстояния небесных тел от Земли. А между тем теория эпициклов допускает различные расстояния светил от Земли в разное время, причем сравнение расстояний светил от Земли, вычисленных на основе измерений видимых их диаметров, с расстояниями их от Земли, выведенными из теории эпициклов, обнаруживает несостоятельность, несообразность этой теории. По теории Птолемея, например, расстояние Луны от Земли колеблется на величину, вдвое большую действительной, вследствие чего видимый диаметр Луны во время перигея (наибольшего приближения) должен быть вдвое больше, чем в апогее (наибольшем удалении), что совершенно противоречит наблюдениям. Однако ни Птолемей, ни его последователи такой проверки не делали и удовлетворялись тем, что теория приблизительно верно определяла место светила на небесном своде.

Чрезвычайно интересно то, что хотя птолемеева система мира является геоцентрической, в ней Солнце играет довольно важную роль (что не было замечено Птолемеем). Дело в том, что Меркурий и Венера (так называемые нижние планеты) никогда не видны в части неба, прямо противоположной Солнцу, т. е. они не наблюдаются в противостоянии с Солнцем. А между тем, это несомненно имело бы место, если бы вселенная была устроена согласно с системой Птолемея. В связи с этим Птолемей допускал, что Меркурий и Венера движутся так, что центры их эпициклов всегда расположены на прямой, идущей от Земли к Солнцу, и потому эти планеты далеко от Солнца не отходят и не могут быть видны на противоположной Солнцу части неба. Так как система Птолемея стремится дать возможность вычислить только месторасположение небесного светила на небосводе, то можно было бы совсем устранить деференты Меркурия и Венеры и принять, что они обращаются по эпициклам с центрами в Солнце. Расстояние Меркурия от Солнца было бы тогда почти вдвое меньше расстояния Венеры (как мы поток увидим, такая система существовала в древности).

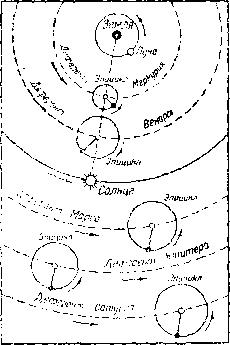
Фиг. 16. Характерная особенность системы Птолемея. Центры эпициклов Меркурия и Венеры лежат на прямой, соединяющей Солнце и Землю, а эпициклы Марса, Юпитера и Сатурна описываются этими планетами в течение года и радиусы их, направленные к планете, всегда параллельны направлению с Земли на Солнце.

Что же касается Марса, Юпитера и Сатурна (так называемых верхних планет), то их можно видеть и в стороне, где находится Солнце, и в противоположной стороне, и поэтому положения центров их эпициклов не связаны с Солнцем. Но для определения положения какой?нибудь из этих планет на эпицикле, необходимо провести через центр его радиус, параллельный направлению с Земли на Солнце, и тогда на конце его окажется планета. А раз для этих планет радиус эпицикла всегда параллелен направлению от Земли к Солнцу, то и в их положениях Солнце имеет особое значение. Поэтому такой эпицикл назывался большим или главным, причем его радиус должен был совершать оборот в течение года, т. е. двигаться сообразно с видимым движением Солнца, и в том же направлении.

Итак, в системе Птолемея движения планет около Земли зависели от их положения относительно Солнца, которое, по понятиям древних, само было одной из планет. Последователи системы Птолемея, однако, не обращали внимания на это обстоятельство или же совершенно не догадывались о том, что оно свидетельствует об обращении планет вокруг Солнца.

Теория эпициклов, разработанная Птолемеем с поразительной тщательностью и, очевидно, не без колоссальных усилий, для времени своего возникновения, когда другие отрасли знания находились еще в самом зачаточном состоянии, была высоко развитой наукой. Птолемей, видя сложность своей теории, говорил, что в движениях небесных тел нельзя ожидать той простоты движения, какую мы видим на Земле. В своем «Альмагесте» он писал: «Нас не должна устрашать многосложность гипотез или же трудность вычисления, а мы должны единственно заботиться о том, чтобы по возможности удовлетворительнее объяснять явления природы». При этом он спрашивал: «Зачем удивляться сложному движению небесных тел, если самая сущность их вовсе неизвестна?» И это «разъяснение», исходившее от лица, которым собственно кончается историк греческой науки о небе, целиком удовлетворяло астрономов, физиков и философов в течение целых 14 столетий.

Однако, для согласования новых наблюдений с планетной теорией Птолемея, астрономы вынуждены были беспрерывно делать к этой теории новые пристройки, ввести в нее дополнительные эпициклы. В XIII в. было уже 75 кругов, заключенных один в другой, так что король Альфонс X Кастильский на созванном им в Толедо в 1250 г. астрономическом конгрессе не мог не указать ученым на то, что подобная запутанность движения светил не достойна вели- 58

кого творца вселенной. Он сказал: «Если бы господь бог при сотворении мира сделал мне честь спросить моего совета, то многое было бы создано получше, а главное — попроще».

Эти слова Альфонса были первым выражением сомнения в правильности общепринятой, но чрезвычайно громоздкой системы Птолемея, построенной на основах геоцентризма, и за них впоследствии король поплатился короной. Ибо тогда считалось еретическим, богохульным все то, что в той или иной мере не гармонировало с геоцентрическим мировоззрением, антропоцентризмом и т. п.

Несостоятельность системы Птолемея обнаруживалась еще в следующем. Сущность всей системы заключается в допущении, что круговую орбиту около Земли описывает не самая планета, а нематериальный центр, т. е. воображаемая математическая точка другого меньшего круга — эпицикла, по которому уже движется планета. А между тем, ни Птолемей, ни его последователи не могли ответить на вопрос, что именно заставляет планету обращаться вокруг совершенно пустого места? Пришлось допустить, что всякий центр эпицикла служит местопребыванием какой?то таинственной, сверхъестественной силы, которая движет планету по окружности. К тому же выходило, что каждая планета в течение суток должна вместе со всеми звездами совершать оборот вокруг Земли! Некоторые средневековые «мудрецы», придя в ужас от сложности всех этих перепутанных между собой движений, решили, что каждая планета наделена особым «духовным руководителем». Это божественное существо невидимой рукой управляет движением планеты по небесной сфере, следя за тем, чтобы она не сбилась со своего пути…

Некоторые ученые считают, что система эпициклов является лишь геометрической абстракцией, что она не претендовала на то, чтобы дать точное изображение действительности. Они полагают, что Птолемей не принимал эпициклы за реально существующие круги, что он приписывал им только геометрическое значение, не касаясь вопроса об их истинной природе. Действительно в «Альмагесте» имеется выражение, которое может быть понято в том смысле, что сам Птолемей смотрел на эпициклы только как на воображаемые круги, по которым происходит движение небесных светил. Но в те времена почти не было ученых, которым была бы доступна такая абстракция, и поэтому астрономы думали, что эпициклы суть нечто действительно существующее. Как бы то ни было, с постепенным усложнением системы Птолемея применение теории эпициклов становилось настолько трудным, что в конце концов должна была появиться мысль: не является ли эта теория лишь «вспомогательной гипотезой», лишь математической фикцией, полезной для вычисления видимого движения планет?

Важно, что в средние века, вплоть до XVI в., сочинение Птолемея считалось астрономическим евангелием и на всю его схему смотрели как на подлинное выражение действительности. Все это время весьма твердо держалась вера в реальность не только птолемеевых кругов, но и твердых сфер. Представлялось, что по поверхности сфер, как в колее катятся центры эпициклов. Тихо Браге заслуженно гордился тем, что ему впервые удалось «разбить небесные сферы». Установив, что кометные орбиты далеко простираются за орбиту Луны и даже Венеры, он тем самым справедливо считал доказанным невозможность существования твердых прозрачных сфер.

В продолжение всего времени от Птолемея до Коперника теоретическая астрономия не сделала почти никаких успехов. Правда, уже в средние века чувствовалась необходимость усовершенствования приведенных Птолемеем таблиц движения планет, потому что всякое новое наблюдение свидетельствовало о недостаточности теории эпициклов: вместо^ того чтобы служить подкреплением теории, оно противоречило ей. Но у астрономов даже не зарождалось мысли о необходимости отказаться от теории, и поэтому они придумывали только некоторые поправки к ней, пытаясь добавлять новые эпициклы к прежним и при этом изменять отношения между радиусами деферентов и эпициклов. Поэт Мильтон говорил об астрономах той эпохи: «И населили они небо концентрическими и эксцентрическими кругами, взгромоздили эпициклы над эпициклами, орбиты над орбитами!»

Несмотря на гибкость, свойственную птолемеевой теории, никогда астрономы не могли добиться того, чтобы вычисленные на основе этой теории положения планет на небосводе полностью согласовались с данными точных наблюдений. В результате же беспрерывного добавления новых эпициклов число этих кругов в конце концов возросло до того, что система эпициклов представляла полнейший хаос и невольно должна была появиться мысль о произвольности подобных допущений.

Однако отбросить эпициклы не решился даже Коперник, так как он не сомневался в том, что все небесные тела движутся равномерно по кругам. Поэтому, решительно отвергнув основное, исходное положение Аристотеля и Птолемея о центральном положении Земли во вселенной, он все же не мог отказаться от эпициклов. Таким образом, учение Коперника, при всем своем огромном астрономическом и культурно — историческом революционном значении, имело весьма существенный недостаток: оно было теорией эпициклов, переработанной на новой гелиоцентрической основе. Этот недостаток теории Коперника был устранен только Кеплером, но и он сначала не решался посягнуть на эпициклы и думал, что несогласие теории эпициклов с позднейшими наблюдениями вызвано великими переменами, происшедшими на небесном своде со времени Птолемея…