23. Ограничение гравитации

23. Ограничение гравитации

Проблема гравитации в пяти измерениях

Если балк существует, его пространство должно быть искривленным. Не будь оно искривлено, гравитация подчинялась бы закону обратных кубов вместо закона обратных квадратов, и тогда Солнце не смогло бы удержать рядом свои планеты – они разлетелись бы в разные стороны.

Ладно-ладно, я не буду спешить и объясню подробнее. Вспомним (из главы 2), что силовые линии гравитационного поля Солнца (как и Земли и любых других сферических тел) устремлены к его центру и притягивают объекты к Солнцу в радиальном направлении (рис. 23.1). Сила гравитационного притяжения Солнца пропорциональна плотности силовых линий (количеству линий, проходящих через заданную площадь). А поскольку поверхности вложенных одна в другую сфер, через которые проходят линии, имеют два измерения, плотность линий уменьшается с увеличением радиуса сферы r как 1/r2, и так же уменьшается сила гравитации. Это ньютоновский закон обратных квадратов для гравитации.

Рис. 23.1. Силовые линии гравитационного поля вокруг Солнца

Теория струн утверждает, что в балке гравитация тоже описывается силовыми линиями. Если пространство балка не искривлено, то силовые линии гравитационного поля Солнца будут радиально распространяться наружу, в балк (рис. 23.2). Поскольку балк обладает дополнительным измерением (в «Интерстеллар» всего одним), есть не два, а три перпендикулярных измерения, в которых гравитация может распространяться. Следовательно, если балк существует и не искривлен, плотность силовых линий, а значит, и сила гравитации должны при удалении от Солнца уменьшаться как 1/r3, а не как 1/r2[68]. Солнечное притяжение, действующее на Землю, будет в 200 раз слабее, а действующее на Сатурн – в 2000 раз слабее. Этак Солнце не сможет удержать планеты рядом с собой, и они улетят прочь, в межзвездное пространство.

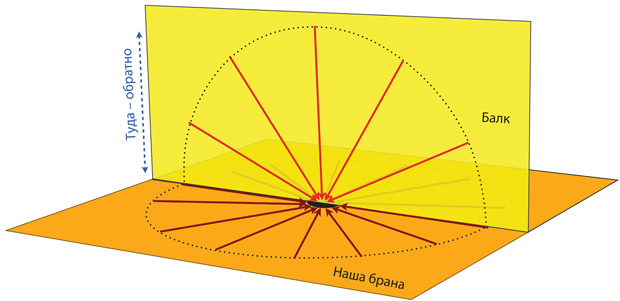
Рис. 23.2. Силовые линии гравитационного поля распространяются в балке радиально, если балк не искривлен. Пунктирные окружности изображены здесь лишь для наглядности (Перерисовка с иллюстрации из книги Лизы Рэндалл «Закрученные пассажи: Проникая в тайны скрытых размерностей пространства» [Рэндалл 2011].)

Однако планеты никуда не улетают, и их поведение однозначно показывает, что солнечная гравитация убывает как обратный квадрат расстояния. Отсюда следует неизбежный вывод: если балк существует, он должен быть искривлен таким образом, чтобы гравитация не могла распространяться в пятое измерение, в измерение «туда – обратно».

Данный текст является ознакомительным фрагментом.