Глава 13 ПРИБЛИЖЕНИЕ НЕЗАВИСИМЫХ ЧАСТИЦ

We use cookies. Read the Privacy and Cookie Policy

Глава 13

ПРИБЛИЖЕНИЕ НЕЗАВИСИМЫХ ЧАСТИЦ

§ 1. Спиновые волн

§ 2. Две спиновые волны

§ 3. Независимые частицы

§ 4. Молекула бензола

§ 5. Еще немного органической химии

§ 6. Другие приме­нения прибли­жения

§ 1. Спиновые волны

В гл. 11 мы разработали теорию распро­странения электрона или любой другой «частицы», например атомного возбуждения, вдоль кристаллической решетки. В предыдущей главе мы эту теорию применили к полупроводникам. Но хотя электронов у нас всегда было много, мы тем не менее неизменно пренебрегали каким-либо взаимодействием между ними. Это, конеч­но, было не более чем приближение, и мы сейчас постараемся глубже разобраться в самой мысли о том, что взаимодействием между элект­ронами разрешается пренебрегать. Мы к тому же воспользуемся возможностью продемонстри­ровать новые применения теории распростране­ния частиц. Поскольку мы по-прежнему будем продолжать пренебрегать взаимодействием меж­ду частицами, то фактически в этой главе будет очень мало нового, разве что новые при­ложения. Однако первый пример, который мы хотим рассмотреть,— это пример, в котором есть возможность совершенно точно выписать правильные уравнения для случая, когда «частиц» больше чем одна. Из них мы сможем увидеть, как делается приближение пренебре­жения взаимодействием. Впрочем, мы не будем слишком тщательно анализировать эту про­блему.

В качестве первого примера рассмотрим «спиновую волну» в ферромагнитном кристалле.

Теории ферромагнетизма мы касались в гл.36 (вып. 7). При нулевой температуре все спины электронов, которые дают вклад в магнетизм всего ферромагнитного кристалла, параллельны между собой. Между спинами существует энер­гия взаимодействия, которая ниже всего тогда, когда все спины направлены вниз. Но при ненулевой темпера­туре имеется какая-то вероятность того, что часть спинов перевернется. Эту вероятность тогда мы приближенно под­считывали. На этот раз мы разовьем квантовомеханическую теорию явления, чтобы знать, что делать, если нужно будет решить задачу точнее. Но мы все еще будем прибегать к идеали­зации; будем считать, что электроны расположены вблизи ато­мов, а спины взаимодействуют только со своими соседями.

Рассмотрим такую модель: пусть в каждом атоме все элект­роны, кроме одного, спарены, и весь магнитный эффект обязан тому, что в каждом атоме остается один неспаренный электрон со спином 1/2. Вообразим еще, что эти электроны расположены в тех самых узлах решетки, где находятся атомы. Модель в об­щих чертах отвечает металлическому никелю.

Кроме того, допустим, что любая пара вращающихся со­седей-электронов взаимодействует друг с другом и что каж­дое такое взаимодействие добавляет в энергию системы по сла­гаемому;

Здесь sпредставляют собой спины, а суммирование идет по всем парам соседей-электронов. Мы уже говорили о по­добной энергии взаимодействия, рассматривая сверхтонкое расщепление водорода, вызываемое взаимодействием магнитных моментов электрона и протона в атоме водорода. Тогда мы выра­жали это в виде Аsе·sр. На этот раз для данной пары, скажем для электронов из атома № 4 и из атома № 5, гамильтониан имеет вид —Ks4·s5. Каждая такая пара дает по одному слагае­мому, а весь гамильтониан (как это бывает и с классическими энергиями) есть сумма таких слагаемых для каждой взаимо­действующей пары. Энергия написана с множителем —К, так что положительное К отвечает ферромагнетизму, т. е. тому слу­чаю, когда наинизшая энергия получается при параллельности соседних спинов. В реальном кристалле могут появиться и другие слагаемые — взаимодействие с соседом через одного и т. д., но на нашем уровне такие усложнения нам не пона­добятся.

Располагая гамильтонианом (13.1), мы обладаем и полным описанием ферромагнетика (в рамках нашего приближения), так что из него должны получиться все магнитные свойства. Кроме того, из него же должны получаться и термодинамические свойства при намагничивании. Если мы сможем определить все уровни энергии, то можно будет найти и свойства кристалла при температуре Т, основываясь на том, что для системы вероят­ность оказаться в данном состоянии с энергией Е пропорцио­нальна 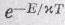. Эта задача никогда не была решена до конца.

Некоторые задачи мы сможем разобрать на простом примере, когда все атомы лежат на одной прямой — случай одномерной решетки. Все эти представления вы потом легко сможете распро­странить на трехмерную решетку. Возле каждого атома имеется электрон; у него есть два возможных состояния — либо спином вверх, либо вниз, и вся система описывается перечислением на­правлений спинов. В качестве гамильтониана системы возьмем оператор энергии взаимодействия. Интерпретируя спиновые векторы (13.1) как сигма-операторы, или сигма-матрицы, мы напишем для линейной решетки

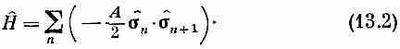
В этом уравнении для удобства написан множитель А/2 (так что некоторые из дальнейших уравнений в точности совпадут с уравнениями из гл. 11).

Каково же наинизшее состояние системы? Состояние наинизшей энергии это то состояние, когда все спины параллельны, скажем все глядят вверх. Это состояние можно обозначить ! ... + + + + ...>, или|осн.), чтобы подчеркнуть, что оно «ос­новное», наинизшее. Энергию этого состояния легко себе пред­ставить. Можно, например, расписать все сигма-векторы через s^х, s^уи s^г, аккуратно подсчитать, каков вклад каждого из них в энергию основного состояния, и все затем сложить. Путь, однако, можно сильно сократить. В гл. 10, § 2 (вып. 8) мы ви­дели, что s^i·s^jможет быть выражено через спин-обменный опе­ратор Паули:

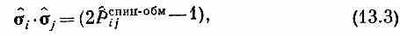
где оператор р^ijспин-°бм обменивает спины i-го и j-го электронов. После этой подстановки гамильтониан обращается в

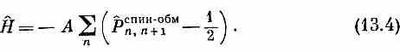
Теперь уже легко подсчитать, что происходит в различных со­стояниях. Например, если и i и j смотрят вверх, то обмен спи­нами ничего не меняет, так что P^ij, действуя на состояние, опять приводят к тому же состоянию, т. е. оно равнозначно умножению на +1. Выражение Р^ij -1/2 просто равно 1/2. (В дальнейшем слова «спин-обм» над Р мы писать не будем.)

В основном состоянии все спины направлены вверх; значит, обмен любой парой спинов приводит опять к исходному состоя­нию. Основное состояние является стационарным. Если подейст­вовать на него гамильтонианом, получится опять то же состоя­ние, умноженное на сумму чисел —(А/2), по одному на каждую пару спинов. Иначе говоря, энергия системы в основном состоя­нии составляет по —А/2 на атом.

Теперь подсчитаем энергии некоторых возбужденных состоя­ний. Удобно будет отсчитывать энергии от основного состояния, т. е. в качестве нулевой энергии выбрать энергию основного состояния. Этого можно добиться, добавив к каждому слагаемо­му в гамильтониане по энергии А/2. Тогда 1/2 в (13.4) просто заменится единицей. Наш новый гамильтониан будет равен

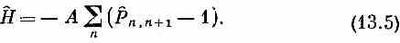
При таком гамильтониане энергия низшего состояния равна нулю; спин-обменный оператор равнозначен умножению на единицу (для основного состояния), что сокращается с единицей в каждом слагаемом.

Для описания состояний, отличных от основного, нам пона­добится своя совокупность базисных состояний. Удобно подойти к делу так: сгруппировать состояния в соответствии с тем, у скольких электронов спин направлен вниз: у одного ли, у двух и т. д. Конечно, состояний, когда один спин направлен вниз, очень много: он может быть опрокинут, скажем, у атома № 4 или у № 5, или у № 6... И можно, конечно, в качестве базисных состояний выбрать именно такие состояния, обозначив их |4>, |5>, | 6>, ... Однако для дальнейшего удобнее, если мы будем отмечать «из ряда вон выходящий атом» (тот, у которого спин направлен вниз) его координатой х. Иначе говоря, мы опре­делим состояние | х5> как такое, в котором все электроны вра­щаются спинами вверх, и один только (тот, что возле атома в точке х5) вращается спином вниз (фиг. 13.1).

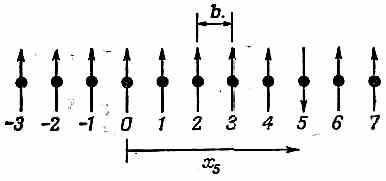
Фиг. 13.1. Базисное состояние |x5> системы спинов, расположенных по одной линии.

Все спины направлены вверх, а тот, что в х5, перевернут.

Вообще, |хn> будет обозначать состояние с одним перевернутым спином, рас­положенным в координате хn n-гоатома.

Как же действует гамильтониан (13.5) на состояние |x5>? Один из членов гамильтониана это, скажем, — А (Р^7,8-1). Оператор P^7,8 обменивает спинами два соседних атома № 7 и № 8. Но в состоянии |x5> они оба направлены вверх, так что ничего не меняется; Р^7,8 равнозначно умножению на единицу:

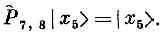
Отсюда следует

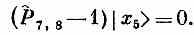
Стало быть, все члены гамильтониана, кроме тех, куда вхо­дит атом № 5, дадут нуль. Операция P^4,5, действуя на со­стояние |x5>, обменивает спинами атом № 4 (со спином вверх) и атом № 5 (со спином вниз). В результате появляется со­стояние, в котором все спины смотрят вверх, кроме атома в точке 4. Иначе говоря,

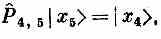
Точно так же

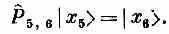
Значит, изо всего гамильтониана выживут только члены

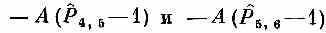
Действуя на |x5>, они дадут соответственно

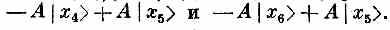
В итоге

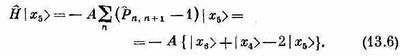
Когда гамильтониан действует на состояние |x5>, то возни­кает некоторая амплитуда оказаться в состояниях | x4> и |х6>. Это просто означает, что существует определенная амплитуда того, что направленный книзу спин перепрыгнет к соседнему атому. Значит, из-за взаимодействия между спинами, если вна­чале один спин был направлен вниз, имеется некоторая ве­роятность того, что позднее вместо него вниз будет смотреть другой. При действии на состояние | хn>гамильтониан дает

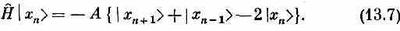
Заметьте, в частности, что если взять полную систему состоя­ний только с одним спином-«перевертышем», то они будут перемешиваться только между собой. Гамильтониан никогда не перемешает эти состояния с другими, в которых спинов-«перевертышей» больше. Пока вы только обмениваетесь спинами, вы никогда не сможете изменить общего количества перевертышей. Удобно будет использовать для гамильтониана матричное обозначение, скажем,

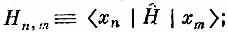
уравнение (13.7) эквивалентно следующему:

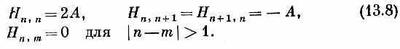
Каковы же теперь уровни энергии для состояний с одним перевернутым спином? Пусть, как обычно, Сn— амплитуда того, что некоторое состояние |y> находится в состоянии |xn>. Если мы хотим, чтобы |y> было состоянием с определенной энергией, то все Сnобязаны одинаково меняться со временем, а именно по правилу

Подставим это пробное решение в наше обычное уравнение Гамильтона

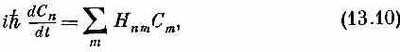
используя в качестве матричных элементов (13.8). Мы, конечно, получим бесконечное количество уравнений, но все их можно будет записать в виде

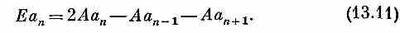
Перед нами опять в точности та же задача, что и в гл. 11, только там, где раньше стояло Е0, теперь стоит 2А. Решения отвечают амплитудам Сn(амплитудам с перевернутым спином), которые распространяются вдоль решетки с константой распростране­ния k и энергией

Е=2A(1-coskb), (13.12)

где b — постоянная решетки.

Решения с определенной энергией отвечают «волнам» перево­рота спина, называемым «спиновыми волнами». И для каждой длины волны имеется соответствующая энергия. Для больших длин волн (малых k) эта энергия меняется по закону

Е=Аb2k2. (13.13)

Как и прежде, мы можем теперь взять локализованный волно­вой пакет (содержащий, однако, только длинные волны), кото­рый соответствует тому, что электрон-«перевертыш» окажется в такой-то части решетки. Этот перевернутый спин будет вести себя как «частица». Так как ее энергия связана с k формулой (13.13), то эффективная масса «частицы» будет равна

Такие «частицы» иногда именуют «магнонами».

§ 2. Две спиновые волны

Теперь мы хотели бы выяснить, что происходит, когда име­ется пара перевернутых спинов. Опять начнем с выбора системы базисных состояний. Выберем такие состояния, когда спины перевернуты в каких-то двух местах (так, как на фиг. 13.2).

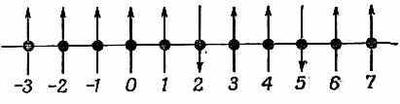
Фиг. 13.2. Состояния с двумя переверну­тыми спинами.

Эти состояния можно, скажем, отмечать x-координатами тех двух узлов решетки, в которых оказались электроны с пе­ревернутым спином. То, что на рисунке, можно обозначить |х2, х5>. В общем случае базисные состояния будут |хn, хm>— дважды бесконечная совокупность! При таком способе описания состояние | x4, х9> и состояние | х9, x4> совпадают, потому что каждое из них просто говорит, что в точках 4 и 9 спин перевер­нут; порядок их не имеет значения. Не имеет также смысла состояние | x4, х4> — такого просто быть не может. Любое со­стояние |y> мы можем описать, задав амплитуды того, что оно обнаружится в одном из базисных состояний.

Итак, Сm,n=<хm,хn|y> теперь означает амплитуду того, что система в состоянии |y> окажется в состоянии, когда у электронов, стоящих вблизи m-го и n-го атомов, спины смотрят вниз. Сложности, которые теперь возникнут, будут связаны не с усложнением идей,— это будут просто усложнения в бухгалтерии. (Одна из сложностей квантовой механики как раз и состоит в громоздкости бухгалтерии. Чем больше спинов перевернется, тем сложнее станут обозначения, тем больше будет индексов, тем страшнее будут выглядеть уравнения; но сами идеи вовсе не обязательно должны усложниться.)

Уравнения движения спиновой системы — это дифферен­циальные уравнения для Сn,m:

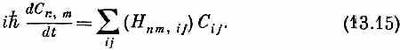
Пусть нам опять нужно найти стационарные состояния. Как обычно, производные по времени обратятся в Е, умноженное на амплитуду, a Cm,n, заменятся коэффициентами аm,n. Затем надо аккуратно рассчитать влияние Н на состояние с перевернутыми спинами т и п. Это сделать нетрудно. Представьте на минуту, что т далеко от n, так что не нужно думать, что будет, если ... и т. д. Обменная операция, производимая в точке хn, передвинет перевернутый спин либо к (n+1)-му, либо к (n-1)-му атому, так что имеется ненулевая амплитуда того, что теперешнее состояние получилось из состояния |хm, хn+1>, и амплитуда того, что оно произошло из состояния |хm, хn-1>. Но передви­нуться мог и второй спин, так что не исключена и какая-то амплитуда того, что Сm,nпитается от Сm+1,n или от Сm-1,n. Все эти эффекты должны быть одинаковы. Окончательный вид гамильтонова уравнения для Сm.nтаков:

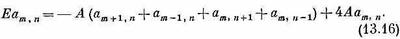
Это уравнение пригодно всегда, за исключением двух слу­чаев. При m=n уравнения вообще нет, а при m=n±1 пара членов в (13.16) должна пропасть. Этими исключениями мы пренебрежем. Мы просто будем игнорировать тот факт, что не­которые из этих уравнений слегка меняются. Ведь как-никак кристалл считается бесконечным и слагаемых в гамильтониане бесчисленно много; пренебрежение некоторым их числом вряд ли сильно на чем-то скажется. Итак, в первом грубом прибли­жении давайте позабудем об изменениях уравнений. Иными сло­вами, допустим, что (13.16) верно при всех m и n, даже когда m и n стоят по соседству. Это самое существенное в нашем прибли­жении.

Теперь уже решение отыскать нетрудно. Мы немедленно по­лучаем

где

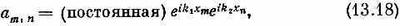
а

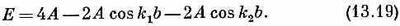
Поразмыслим минутку о том, что было бы, если бы у нас были две независимые, отдельные спиновые волны (как в пре­дыдущем параграфе), соответствующие k=k1и k=k2; их энер­гии из (13.12) имели бы вид

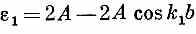
и

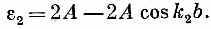
Заметьте, что энергия Е в (13.19) является как раз их суммой:

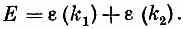
Иными словами, наше решение можно толковать следующим образом. Имеются две частицы, т. е. пара спиновых волн, одна из которых обладает импульсом, описываемым числом k1a другая — числом k2; энергия системы равна сумме энергий этих двух объектов. Обе частицы действуют совершенно независи­мо. Вот и все, что в этом есть — и ничего больше.

Конечно, мы сделали некоторые приближения, но в данный момент мы не будем обсуждать точность нашего ответа. Вы, однако, чувствуете, что в кристаллах разумного размера с миллиардами атомов и, стало быть, с миллиардами слагаемых в гамильтониане большой ошибки от пренебрежения немногими слагаемыми не выйдет. Если бы, конечно, перевернутых спинов стало так много, что их плотность была бы заметной, то при­шлось бы позаботиться и о поправках.

(Интересно, что в случае, когда перевернутых спинов только два, можно написать и точное решение. Но результат особой важности не представляет. Просто интересно, что в этом случае уравнения можно решить точно. Решение таково:

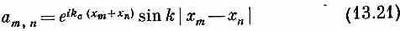
с энергией

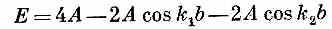
и с волновыми числами kcи k, связанными с k1 и k2формулами

k1= kc-k, k2=kc+k. (13.22)

В этом решении отражено и «взаимодействие» пары спинов. Оно описывает тот факт, что когда спины сближаются, возникает какая-то вероятность их рассеяния. Поведение спинов очень по­хоже на взаимодействие частиц. Но подробная теория их рас­сеяния выходит за пределы того, о чем мы здесь собрались го­ворить.)

§ 3. Независимые частицы

В предыдущем параграфе мы написали гамильтониан (13.15) для двухчастичной системы. Затем, пользуясь приближением, эквивалентным пренебрежению каким-либо «взаимодействием» между двумя частицами, мы нашли стационарные состояния, описываемые формулами (13.17) и (13.18). Это состояние по­просту есть произведение двух одночастичных состояний. Но решение, которое мы написали для аm,n[формула (13.18)], на самом деле удовлетворить нас не может. Мы с самого начала подчеркивали, что состояние | х9, x4> не отличается от состоя­ния |x4, x9), что порядок хmи хnневажен. Вообще говоря, алгеб­раическое выражение для амплитуды Сm,nне должно меняться от перестановки значений хmи хn, потому что она не изменяет состояния. В любом случае она будет представлять амплитуду того, что спин, направленный вниз, обнаружится в хmи в хn.

Но обратите внимание, что (13.18) несимметрично по хmи хn, поскольку k1и k2, вообще говоря, различны.

Все дело в том, что мы не заставили наше решение (13.15) подчиниться этому добавочному условию. К счастью, пока не­трудно все исправить. Заметьте, во-первых, что ничуть не хуже формулы (13.18) другое решение уравнения Гамильтона:

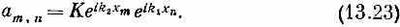
И даже энергия здесь та же самая, что была в (13.18). Значит, любая линейная комбинация (13.18) и (13.23) также будет ре­шением системы и будет обладать по-прежнему энергией, давае­мой (13.19). Решение, которое нужно выбрать по требованиям симметрии,—просто сумма (13.18) и (13.23):

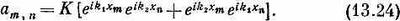
Теперь при данных k1и k2 амплитуда Сm,nне зависит от того, в каком порядке мы берем хmи хn;если мы случайно поставим хmи хnв обратном порядке, мы получим ту же амплитуду. И на­ше толкование уравнения (13.24) на языке «магнонов» тоже ста­нет иным. Уже нельзя говорить, что уравнение представляет одну частицу с волновым числом k1 и другую частицу с волновым числом k2. Амплитуда (13.24) представляет одно состояние с двумя частицами (магнонами). Состояние характеризуется дву­мя волновыми числами k1и k2. Наше решение выглядит как со­ставное состояние одной частицы с импульсом р1= k1/h и дру­гой частицы с импульсом р2=k2/h, но в этом состоянии нельзя сказать, где какая частица.

В этот момент полезно вспомнить гл. 2 (вып. 8) и наш рас­сказ о тождественных частицах. Мы просто только что показали, что частицы спиновых волн (магноны) ведут себя как тождест­венные бозе-частицы. Все амплитуды обязаны быть симметрич­ны по координатам двух частиц; это все равно, что сказать, что после «обмена двумя частицами» мы снова получим ту же амплитуду с тем же знаком. Но вы можете подумать: «Почему же мы все-таки решили в (13.24) сложить два члена? Почему не вычесть?» Ведь при знаке минус обмен хmи хnпросто изменил бы знак аm,n, а это не в счет, это не имеет значения. Но ведь об­мен хmс хn ничего не меняет — все электроны кристалла оста­нутся там же, где и были, так что даже для перемены знака нет, казалось бы, никакого повода. Но это, конечно, плохой ар­гумент.

Наше обсуждение имело двойную цель: во-первых, расска­зать вам кое-что о спиновых волнах; во-вторых, продемонстри­ровать состояние, амплитуда которого равна произведению двух амплитуд, а энергия равна сумме энергий, отвечающих этим амплитудам. Для независимых частиц амплитуда получается умножением, а энергия — сложением. Почему сложением — легко понять. Энергия — это коэффициент при t в мнимом пока­зателе экспоненты; она пропорциональна частоте. Если пара объектов что-то совершает, один с амплитудой 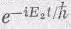, а другой . с амплитудой 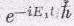, и если амплитуда того, что обе эти вещи произойдут вместе, является произведением отдельных ампли­туд, то в произведении появится единственная частота, равная сумме двух частот. Энергия, отвечающая произведению ампли­туд, есть сумма обеих энергий.

Нам понадобилось довольно долго говорить, чтобы сообщить очень простую вещь: когда вы не учитываете взаимодействия между частицами, вы вправе рассматривать каждую частицу независимо. Они могут отдельно существовать во всевозможных состояниях, в которых они пребывали бы и порознь, и давать тот же вклад в энергию, какой давали бы порознь. Однако сле­дует помнить, что если частицы тождественны, то они могут вести себя как бозе- или ферми-частицы в зависимости от за­дачи. Например, пара электронов, добавленная к кристаллу, ведет себя как ферми-частицы. Обмен местоположениями двух электронов приводит к перемене знака амплитуды. В уравне­нии, соответствующем (13.24), между двумя слагаемыми стоит знак минус. Как следствие этого: две ферми-частицы не могут пребывать в точности в одних и тех же условиях — с одинако­выми спинами и одинаковыми k. Амплитуда такого состояния нуль.

§ 4. Молекула бензола

Хотя квантовая механика снабжает нас основными закона­ми, определяющими строение молекул, эти законы, однако, удается точно применить лишь к самым простым соединениям. Поэтому химики разработали различные приближенные спосо­бы расчета некоторых из свойств сложных молекул. Мы хотим здесь рассказать, как химики-органики применяют приближе­ние независимых частиц. Начнем с молекулы бензола. Мы ее рассматривали с другой точки зрения в гл. 8 (вып. 8). Тогда мы воспользовались приближенным представлением молекулы в виде системы с двумя состояниями, базисные состояния которой показаны на фиг. 13.3. Имеется кольцо из шести углеродов, к каждому из которых приделано по водороду. По принятой схеме валентных связей необходимо допустить, что между поло­виной атомов углерода имеются двойные связи и что в низших энергетических условиях воз­никают две возможности, по­казанные на рисунке. Но, кроме этого, имеются и еще другие, более высокоэнерге­тические состояния. Когда мы в гл. 8 говорили о моле­куле бензола, мы пользова­лись только двумя состоя­ниями, а прочие забыли. И мы обнаружили, что энергия основного состояния молекулы не совпадала с энергией ни одного из нарисованных состояний; нет, она была ниже на величину, пропорциональную амплитуде переброса из одного такого состояния в другое.

А теперь мы хотим взглянуть на ту же молекулу с совершен­но иной точки зрения, применяя приближение другого рода. Обе точки зрения приведут нас к разным ответам, но когда мы усовершенствуем оба приближения, то придем к истине — к правильному описанию бензола.

Однако если не позаботиться об этих усовершенствованиях (что обычно и делают), то не нужно удивляться, что эти описа­ния не сойдутся. Мы по крайней мере покажем, что при новой точке зрения низшая энергия молекулы бензола оказывается ниже, чем у любой из структур с тремя двойными связями (см. фиг. 13.3).

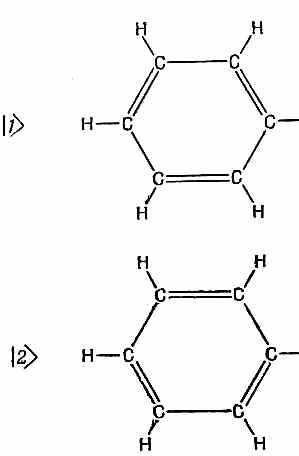
Фиг. 13.3. Два базисных состоя­ния молекулы бензола, исполь­зовавшиеся в гл. 8.

Рассмотрим следующую картину. Представим себе шесть ато­мов водорода, связанных только одиночными связями (фиг. 13.4).

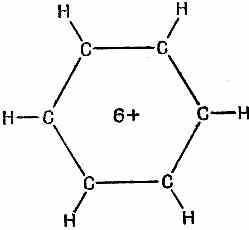
Фиг. 13.4. Бензольное кольцо, из которого убрали шесть электронов.

Мы убрали шесть электронов (поскольку каждая связь обоз­начает пару электронов), так что перед нами шестикратно ионизованная молекула бензола. Теперь посмотрим, что слу­чится, когда мы поодиночке вернем в молекулу всю шестерку электронов, считая, что каждый из них может свободно двигать­ся вокруг кольца. Допустим также, что все связи, показанные на фиг. 13.4, заполнены и не нуждаются в дальнейшем рассмотре­нии. Что происходит, когда мы возвращаем молекулярному иону его электрон? Он, конечно, может расположиться в любом из шести мест на кольце, соответствующих шести базисным со­стояниям. И у него будет некоторая амплитуда (скажем А) того, что он перейдет с одного места на другое. При анализе стационарных состояний обнаружатся несколько возможных уровней энергии. Это только при одном электроне.

Добавим еще один электрон. И сделаем теперь самое стран­ное предположение: то, что делает один электрон, не сказывается на том, что делает другой. На самом деле они, конечно, будут взаимодействовать; они отталкивают друг друга с помо­щью кулоновых сил, и, кроме того, их энергия, когда они по­падают в одно место, должна заметно отличаться от удвоенной энергии, когда они туда попадают поодиночке. Конечно, приб­лижение независимых частиц незаконно, когда мест только шесть, особенно когда в них хотят поместить шестерку электро­нов. Но, несмотря на это, химики-органики сумели многому научиться, делая именно такое приближение.

Прежде чем подробно рассчитывать молекулу бензола, возь­мем пример попроще — молекулу этилена. В нее входят только два атома углерода и по паре атомов водорода с каждой сторо­ны (фиг. 13.5).

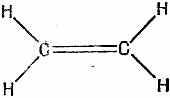
Фиг. 13.5. Молекула этилена.

У молекулы есть одна «лишняя» связь между двумя атомами углерода, в которую входят два электрона. Уберем один из этих электронов; что мы получим? То, что оста­нется, можно будет рассматривать как систему с двумя состоя­ниями: оставшийся электрон может находиться либо возле од­ного атома, либо возле другого. И, как у всякой системы с двумя состояниями, допустимые энергии отдельного электрона могут быть равны либо Е0-А, либо Е0+А (фиг. 13.6).

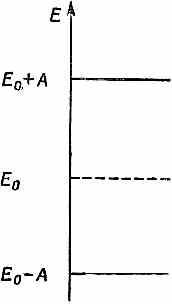
Фиг. 13.6. Возможные уровни энергии «лиш­них» электронов в молекуле этилена.

Добавим теперь второй электрон. Все очень хорошо: электро­нов у нас два — первый можно поставить в нижнее состояние, а второй в верхнее, не так ли? Не совсем,— мы о чем-то забыли. Ведь каждое из со­стояний на самом деле двойное. Когда мы говорим, что допустимо состояние с энер­гией Е0-А, то в действительности там их пара. В одно и тоже состояние могут по­пасть два электрона, один со спином, направленным вверх, другой — вниз (но не больше, из-за прин­ципа запрета). Так что на самом деле имеются два возможных состояния с энергией Е0-А. Можно начертить диаграмму (фиг. 13.7), которая показывает и уровни энергии, и их насе­ленность.

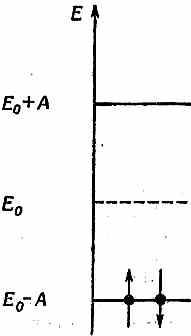
Фиг. 13.7. В добавочной связи молекулы этилена два электрона (один со спином вверх, другой — вниз) могут занять низший уровень энергии.

В состоянии наименьшей энергии оба электрона будут в наинизшем состоянии с противоположными спинами. Энергия «лишней» связи в молекуле этилена поэтому равна 2(Е0-А), если пренебречь взаимодействием между двумя электронами. Теперь вернемся к бензолу. У каждого из двух состояний на фиг. 13.3 есть три двойные связи. И каждая из них очень похожа на связь в этилене и дает вклад в энергию 2(Е0-А), где теперь Е0 — уже энергия, необходимая, чтобы поместить электрон в бензоле на нужное место, а А — амплитуда пере­броса его в соседнее место. Значит, энергия должна быть равна примерно 6(Е0-А). Но когда мы раньше изучали бензол, то пришли к выводу, что его энергия ниже энергии структуры с тремя двойными связями. Посмотрим, получится ли теперь, с нашей новой точки зрения, энергия бензола ниже, чем у трех двойных связей.

Начинаем с шестикратно ионизо­ванного бензольного кольца. Добавляем один электрон. Теперь у нас система с шестью состояниями. Мы пока еще не решали таких систем, но знаем, что нужно делать. Можно написать шесть уравнений для шести амплитуд и т. д. Но не лучше ли сберечь свои силы, ведь мы уже ре­шили эту задачу, исследуя электрон в бесконечной цепочке атомов. Конечно, бензол — не бесконечная цепочка, шесть мест для атомов в нем расположены по кругу. Но представьте, что мы разняли кольцо в цепь и пронумеровали атомы вдоль цепи числами от 1 до 6. В бесконечной линии следующее место имело бы номер 7, но если мы условимся, что оно совпадает с местом номер 1 и т. д., то все окажется в точности похожим на бензольное кольцо. Иными словами, мы можем взять реше­ние для бесконечной линии с добавочным требованием, чтобы решение было периодичным с периодом длиной в шесть атомов. Согласно гл. 11, электрон на прямой обладает состояниями определенной энергии, когда амплитуда того, что он окажется в некотором месте хn, равна . При каждом k энер­гия равна

E=E0-2Acoskb. (13.25)

Теперь из этих решений нам нужно оставить только такие, которые через каждые 6 атомов повторяются. Разберем сперва общий случай, когда в кольце N атомов. Если решение должно иметь период в N атомных расстояний, то eikbNдолжна быть равна единице, или kbN должна быть кратна 2p. Если s — любое це­лое число, то наше условие имеет вид

kbN=2ps. (13.26)

Мы раньше видели, что нет смысла брать k вне пределов ±p/b. Это означает, что мы получим все мыслимые состояния, беря значения s в пределах ±N/2.

Стало быть, мы приходим к тому, что у N-атомного кольца имеется N состояний определенной энергии и их волновые числа ksдаются числами

ks=2ps/Nb. (13.27)

Каждое состояние имеет энергию (13.25). Получается линейча­тый спектр возможных уровней энергий. Спектр для бензола (N=6) показан на фиг. 13.8, б. (Числа в скобках указывают число различных состояний с одинаковой энергией.)

Есть наглядный способ изобразить эти шесть уровней энер­гии. Он показан на фиг. 13.8, а. Вообразим круг с центром на одном уровне с Е0и с радиусом 2А. Если мы отложим, начиная снизу, шесть равных дуг (под углами, считая от нижней точки, ksb = 2ps/N, или 2ps/6 для бензола), то высоты точек круга будут решениями (13.25). Шесть точек представляют шесть возможных состояний. Низший уровень энергии придется на Е0-2А;дальше идут два состояния с одинаковой энергией Е0-А и т. д. Это возможные состояния одного электрона. Если электронов не один, а больше, то в каждое состояние может попасть по два электрона с противоположными спинами.

У молекулы бензола надо здесь разместить шесть электро­нов. Если состояние основное, то они должны попасть в наи­низшие возможные энергетические состояния — пара в s=0, пара в s=+1 и пара в s =-1. Согласно приближению неза­висимых частиц, энергия основного состояния равна

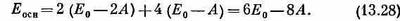
Она действительно оказывается меньше, чем у трех отдельных двойных связей,— на 2А.

Сравнив энергию бензола с энергией этилена, можно опреде­лить А. Эта величина оказывается равной 0,8 эв, или в едини­цах, которые нравятся химикам, 18 ккал/моль.

Этим описанием можно воспользоваться, чтобы вычислить или понять другие свойства бензола. Например, глядя на фиг. 13.8, можно разобраться в возбуждении бензола светом.

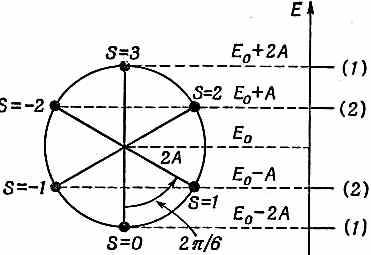
Фиг. 13.8. Уровни энергии в кольце, в котором для электрона приготовлены шесть свободных мест (на­пример, в бензольном).

Что бы произошло, если бы мы попытались возбудить один из электронов? Он мог бы передвинуться к одному из незанятых высших состояний. Наинизшей энергией возбуждения оказался бы переход от наивысшего заполненного уровня к наинизшему пустому. Эта энергия равна 2A. Бензол будет поглощать свет с частотой v=2A/h. Кроме того, будет наблюдаться также по­глощение фотонов с энергиями ЗА и 4A. Нечего и говорить, что спектр поглощения бензола был измерен, и картина спектраль­ных линий оказалась более или менее правильной, если не счи­тать того, что наинизшие переходы наблюдаются в ультрафио­лете; и чтобы удовлетворить всем данным, пришлось бы взять величину А около 1,4—2,4 эв. Иначе говоря, численное значе­ние А вдвое-втрое выше, чем предсказывается энергией хими­ческой связи.

Как же поступает химик в таких случаях? Он анализирует множество молекул сходного типа и выводит какие-то эмпири­ческие правила. Он учит, например: для расчета энергии связи берите вот такое-то и такое-то значение А, а для получения при­ближенно верного спектра поглощения возьмите другое значе­ние A. Вам может показаться, что это звучит слегка абсурдно. И впрямь, в ушах физика, который пытается объяснить всю при­роду из первоначальных принципов, это звучит довольно дико. Но перед химиком задача другая. Он обязан заранее догадаться, что произойдет с молекулами, которых до сих пор не было или которые до конца не поняты. Ему нужен ряд эмпирических пра­вил и ему совершенно все равно, откуда они возьмутся. Так что теорией он пользуется совсем не так, как физик. Он берет урав­нения, в которых отразился свет истины, а потом вынужден менять в них константы, делая эмпирические поправки.

В случае бензола основная причина несогласия лежит в нашем предположении, что электроны независимы; теория, из которой мы исходили, на самом деле незаконна. Тем не менее на нее падает какой-то отблеск истины, потому что результаты, по-видимому, идут в правильном направлении. При помощи таких уравнений плюс некоторые эмпирические правила (со множеством исключений) химик-органик прокладывает свой путь через чащу тех сложнейших вещей, которые он решился изучать. (Не забывайте, что в действительности причина, по которой физику удается выводить что-то из основных принципов, состоит в том, что он выбирает только простые задачи. Он ни­когда не решает задач с 42 или даже с 6 электронами. До сих пор он смог рассчитать с приличной точностью только атом водо­рода да атом гелия.)

§ 5. Еще немного органической химии

Можно ли применить все эти идеи для изучения других молекул? Рассмотрим такую молекулу, как бутадиен (1,3); она показана на фиг. 13.9 с помощью обычной картины валентных связей.

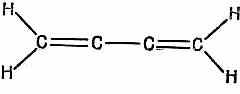
Фиг. 13.9. Изображение с по­мощью валентных связей молекулы бутадиена (1,3).

Мы можем опять затеять те же игры с лишней четверкой электронов, отвечающей двум двойным связям. Если ее убрать, то остается четыре атома углерода по одной линии. А как рас­считывать такую линию, вы уже знаете. «Но позвольте,— скажете вы,—я ведь только знаю, как решать бесконечную ли­нию». Однако решения для бесконечной линии включают также и решения для конечной. Следите. Пусть N — число атомов на прямой; пронумеруем их 1, 2, ..., N (фиг. 13.10).

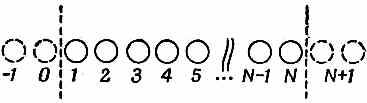
Фиг. 13.10. Отрезок прямой с N молекулами.

В уравне­нии для амплитуды в точке 1 у вас не появится член для пере­хода из точки 0. Точно так же уравнение для точки N будет отличаться от того, которым мы пользовались для бесконечной прямой, потому что никакого вклада точки N+1 не будет. Но представьте, что мы придумали решение для бесконечной прямой со следующим свойством: амплитуда оказаться вблизи атома 0 есть нуль и амплитуда оказаться вблизи атома N+1 тоже нуль. Тогда система уравнений для всех точек от 1 до N на конечной линии также будет удовлетворяться. Казалось бы, таких решений не бывает, ибо все наши решения имеют вид 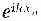и обладают всюду одинаковой абсолютной величиной. Но вспомните, что энергия зависит только от абсолютной вели­чины k, так что другим в равной мере законным решением было бы 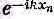. И то же справедливо для любой суперпозиции этих двух решений. Вычитая их, мы получим решение sin kxn, а оно удовлетворяет требованию, чтобы амплитуда при х=0 была нулем. И оно все еще соответствует энергии Е0-2Аcoskb. Далее, подходящим выбором величины k можно также добиться, чтобы амплитуда в xN+1была тоже нулем. Для этого нужно, чтобы (N+1)kb было кратным p, т. е. чтобы

где s — целое число между 1 и N. (Берутся только положительные k, потому что каждое решение содержит и +k, и -k; перемена знака k опять дает то же состояние.) Для молекулы бутадиена N=4, так что имеется четверка состояний с

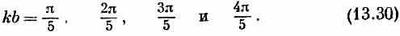
Уровни энергии можно теперь представить, пользуясь кру­говой диаграммой, похожей на бензольную. На сей раз возьмем полукруг, деленный на пять равных частей (фиг. 13.11).

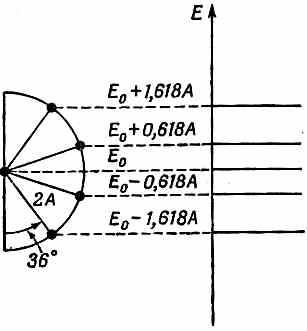
Фиг. 13.11. Энергетические уровни бутадиена.

Точка внизу отвечает s=0, что не дает какого-либо состояния. То же самое справедливо для точки наверху, отвечающей s=N+1. Оставшиеся четыре точки дают четверку разрешенных энергий. Имеется четыре стационарных состояния, чего и следовало ожидать, судя по четырем базисным состояниям. В круговой диаграмме углы равны p/5, или 36°. Наинизшая энергия оказы­вается равной Е0 — 1,618A. (Каких только чудес не бывает в математике! Золотое сечение греков дает нам наинизшее энер­гетическое состояние молекулы бутадиена, как это следует из

нашей теории!)

Теперь уже ясно, как меняется энергия молекулы бутадиена, когда в нее вводят четверку электронов. Эта четверка заполнит два нижних уровня — каждый будет заполнен парой электро­нов с противоположными спинами. Полная энергия будет равна

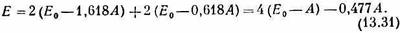
Это выглядит вполне разумно. Энергия чуть пониже, чем просто у двух двойных связей, но связь не так сильна, как в бензоле. Во всяком случае, именно так химик анализирует некоторые ор­ганические молекулы.

Но в его распоряжении есть не только энергии, но и ампли­туды вероятности. Зная амплитуды для каждого состояния и зная, какие состояния заполнены, он может сообщить нам, какова вероятность нахождения электрона в каком-нибудь месте молекулы. Те места, где пребывание электрона более вероятно, вступают в игру при таких химических замеще­ниях, которые требуют, чтобы электрон обслуживал и другую группу атомов. Другие же места молекулы участвуют в таких замещениях, при которых молекула имеет тенденцию передать системе еще один электрон.

Подобные же идеи могут помочь нам получить правильное представление даже о таких сложных молекулах, как хлоро­филл, один из вариантов которого показан на фиг. 13.12.

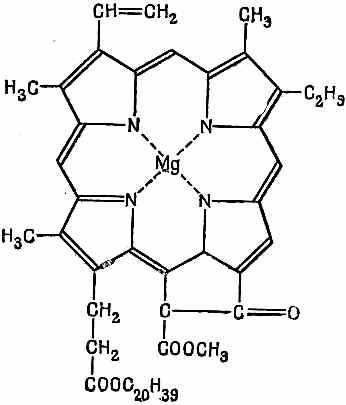
Фиг. 13.12. Молекула хлоро­филла.

Обра­тите внимание, что двойные и одиночные связи образуют длинное замкнутое кольцо с двадцатью интервалами.

Лишние электроны двойных связей могут бегать по этому кольцу. При помощи метода независимых частиц можно получить всю совокупность энергетических уровней. От пе­реходов между этими уровнями возникают сильные линии поглощения, которые лежат в видимой части спектра и при­дают этой молекуле ее густой цвет. И другие сложные мо­лекулы, такие, как ксантофилл, от которого листья по­лучают красную окраску, можно изучить таким же точно способом.

В органической химии при работе с подобного рода теорией использу­ют еще одну идею. Она, пожалуй, самая удачная из всех (или по крайней мере в определенном смы­сле самая точная). Она отвечает на такой вопрос: в каких случаях получается особенно прочная химическая связь? Ответ очень интере­сен. Возьмем вначале для примера бензол и представим ряд со­бытий, которые произойдут, если мы начнем с шестикратно иони­зованной молекулы и примемся добавлять новые и новые электроны. Тогда нужно будет говорить о различных ионах бензола — отрицательных и положительных. Изобразим энер­гию иона (или нейтральной молекулы) как функцию числа элек­тронов. Если мы примем Е0=0 (мы не знаем, чему равно E0), то получим кривую, показанную на фиг. 13.13.

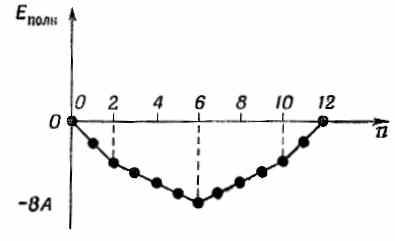
Фиг. 13.13. Сумма всех энергий электронов, ког­да нижние состояния на фиг. 13.8 заполнены n электронами (принято E0=0).

Для первых двух электронов наклон функции постоянен — это прямая линия. Затем для каждой очередной группы электронов он воз­растает, меняясь скачком от одной группы к другой. Наклон изменяется тогда, когда заканчивается заполнение системы уровней с одной энергией и очередному электрону приходится переходить к очередной более высокой системе уровней.

В действительности истинная энергия иона бензола совер­шенно непохожа на фиг. 13.13 из-за взаимодействий электронов и из-за электростатических энергий, которыми мы пренебрегли. Эти поправки, однако, меняются с n довольно плавно. Даже если бы их все учесть, на окончательной энергетической кривой все равно остались бы изломы при таких и, при которых как раз заполняются отдельные уровни энергии.

Рассмотрим теперь очень гладкую кривую, на которой в среднем укладываются все точки (фиг. 13.14).

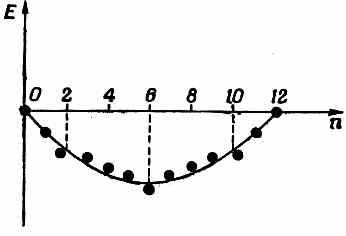
Фиг. 13.14. Точки с фиг. 13.13 и плавная кривая. Молекулы с n=2, 6, 10 устойчивее остальных.

Можно сказать, что точки над этой кривой обладают энергией «выше чем нор­мальной», а точки под нею «ниже чем нормальной». И в общем случае следует ожидать, что у конфигураций с «ниже чем нор­мальной» энергией средняя устойчивость окажется повышенной. Обратите внимание, что конфигурации, которые значительно ниже кривой, всегда оказываются в конце одного из прямоли­нейных отрезков, а именно там, где электронов как раз хватает на то, чтобы заполнить «энергетическую оболочку», как ее на­зывают. Это очень точное предсказание теории. Молекулы и ионы особо устойчивы (по сравнению с прочими подобными кон­фигурациями), когда имеющиеся у них в наличии электроны как раз заполняют энергетическую оболочку.

Эта теория объяснила и предсказала некоторые весьма нео­бычные химические факты. Вот очень простой пример. Возьмем кольцо из трех атомов. Почти невозможно поверить, что химик сможет из трех атомов составить кольцо и сделать его устой­чивым. Но это было сделано. Энергетический круг для трех электронов показан на фиг. 13.15.

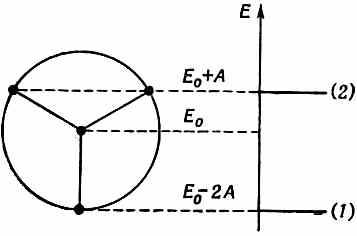
Фиг. 13.15. Энергетиче­ская диаграмма для кольца из трех атомов.

Если поместить в нижнее состояние два электрона, то пойдут в дело только два из трех требуемых электронов. Третий электрон придется поместить на более высокий уровень. Отсюда следует, что молекула не будет слишком устойчивой. Зато двухэлектронная структура обязана быть устойчивой. И действительно, оказывается, что нейтраль­ную молекулу трифенилциклопропанила сделать очень трудно, но зато сравнительно легко соорудить положительный ион, по­казанный на фиг. 13.16.

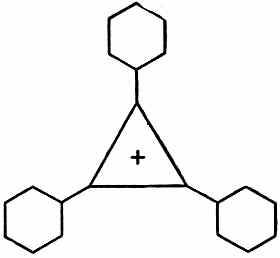
Фиг. 13.16. Катион трифенилииклопропанила.

Правда, кольцо из трех атомов никогда не бывает легко сделать, потому что, когда связи в органической молекуле образуют равносторонний треугольник, всегда появ­ляются большие напряжения. Чтобы соединение было устой­чиво, структуру нужно как-то стабилизировать. Оказывается, что, если поставить по углам три бензольных кольца, можно сделать положительный ион. (Отчего нужно добавлять бензоль­ные кольца, непонятно.)

Подобным же образом можно также проанализировать и пятиугольное кольцо. Если вы начертите энергетическую диа­грамму, то качественно сможете убедиться, что шестиэлектронная структура должна быть особо устойчива, так что такая мо­лекула должна быть устойчивее всего в виде отрицательного иона. И вот кольцо из пяти атомов действительно хорошо из­вестно, легко сооружается и действует всегда как отрицательный ион. Подобным же образом вы легко убедитесь, что кольцо из 4 и 8 атомов не очень интересно, а кольцо из 14 или 10 (как и кольцо из 6) должно быть особенно устойчиво в форме нейт­рального объекта.

§ 6. Другие применения приближения

Есть два других сходных случая, на которых мы остано­вимся лишь вкратце. Говоря о строении атома, можно считать, что электрон заполняет последовательные оболочки. Теорию движения электрона Шредингера удается с легкостью разра­ботать лишь для отдельного электрона, движущегося в «цент­ральном» поле — поле, зависящем только от расстояния от точки. Но как же тогда разобраться в том, что происходит в атоме, в котором 22 электрона?! Один из путей — воспользо­ваться приближением независимых частиц. Сперва вы подсчиты­ваете, что происходит с одним электроном. Получаете сколько-то там уровней энергии. Помещаете электрон в нижнее энерге­тическое состояние. В грубой модели вы продолжаете игнори­ровать взаимодействия электронов и продолжаете заполнять последовательные оболочки, но еще лучшие ответы получатся, если учесть (хотя бы приближенно) влияние электрического заряда электрона. Добавляя электрон, каждый раз вычис­ляйте амплитуду того, что он будет обнаружен в различных местах, и затем с ее помощью прикидывайте вид сферически симметричного распределения заряда. Поле этого распределе­ния (совместно с полем положительного ядра и всех предыдущих электронов) используйте для расчета состояний, доступ­ных очередному электрону. Таким путем вы можете получить вполне разумные оценки энергий нейтрального атома и раз­личных ионизованных состояний. Вы увидите, что и здесь имеются энергетические оболочки, так же как у электронов в кольцевой молекуле. При не совсем заполненной оболочке атом иногда охотнее присоединяет к себе один или несколько элект­ронов, а иногда охотнее их теряет, чтобы прийти в устойчивое состояние, когда оболочка заполнена.

Эта теория объясняет механизм, лежащий в основе самых фундаментальных химических свойств, проявляющихся в пе­риодической таблице элементов. Инертные газы — это те эле­менты, у которых как раз закончилось заполнение оболочки, и их особенно трудно заставить вступать в реакцию. (В действи­тельности, конечно, некоторые из них реагируют, например, с фтором или с кислородом, но в таких соединениях связь очень слаба; так называемые инертные газы инертны лишь отчасти.) Атом, у которого на один электрон больше или на один меньше, чем у инертного газа, легко теряет или присоединяет этот элект­рон, чтобы оказаться в особо устойчивых (низкоэнергетических) условиях, какие возникают от того, что оболочка заполнена до конца,— они являются очень активными химическими элемен­тами с валентностью +1 и -1.