2. Атомы существуют!

Как роковую несправедливость истории науки можно воспринимать то, что Л. Больцман не дожил до осуществления решающих опытов, неопровержимо доказавших реальность существования атомов, результаты которых были истолкованы на основании полученной им барометрической формулы (13). Два года отделили его смерть от полного признания его идей! Как это мало и как долго шел ученый к этому, как много сил затратил он в борьбе за признание их справедливости. Как не хватало Больцману в его ожесточенной дискуссии с представителями различных идеалистических группировок в физике именно этих принципиальных опытов, дающих исследователю столь желанное для него «счастье чувственного восприятия».

Название «решающие» дается таким опытам не случайно. Они подводят черту под множеством исследований того или иного явления, окончательно раскрывая его сущность. К таким опытам можно отнести эксперименты Г.Галилея по измерению ускорения свободного падения, опыты А. А Майкельсона, доказавшие отсутствие эфира, опыты Р. Милликена по определению заряда электрона и т. д. На основании этих опытов рождались новые физические теории — теория всемирного тяготения И. Ньютона, теория относительности А. Эйнштейна. Опыты Р. Милликена дали подтверждение того, что электричество имеет зернистую, дискретную структуру. Это было убедительным доказательством плодотворности атомистических представлений для физики. Опыты по доказательству существования атомов были выполнены в 1908 г. французским ученым Ж. Перреном, и, поскольку они имеют самое непосредственное отношение к теме книги, следует рассказать о них несколько подробнее.

Одним из самых удивительных явлений природы является так называемое броуновское движение. Оно названо так в честь английского ботаника Р. Броуна, открывшего его в 1827 г. Наблюдая в микроскоп взвесь цветочной пыльцы в воде, он заметил, что мельчайшие частицы находятся в непрерывном движении. Траектории частиц были весьма причудливы (см. рис. 3). Движение частиц пыльцы носило ярко выраженный хаотический характер, причина происхождения этого движения была неясной. Многочисленные объяснения броуновского движения не выдерживали проверки временем. Например, сначала было выдвинуто предположение о том, что это движение присуще только частицам органического происхождения (пыльца) и что они движутся за счет присущей им некоей «жизненной силы». Но очень скоро было показано, что такое движение присуще вообще всем малым частицам, находящимся во взвешенном состоянии в жидкости. Броуновское движение пытались связать с дрожанием опор лабораторного стола, на котором находился микроскоп, с влиянием падающего на частицы света, с неравномерным нагревом жидкости, но все эти объяснения были отвергнуты как необоснованные.

Первой правильной догадкой, объясняющей происхождение броуновского движения, было высказанное в 1863 г. О.Винером предположение о том, что его следует связывать с внутренними движениями, присущими самой жидкости. В последующие годы ряд исследователей, в частности в 1888 г. Л. Гюи, показали, что причиной броуновского движения является тепловое движение молекул жидкости, приводящее к столкновению их со взвешенными в жидкости малыми частицами. Это объяснение имело принципиально важное значение для науки, ибо давало в руки исследователям первое наглядное свидетельство теплового движения частиц материи. Однако и оно еще долгое время было уязвимым, поскольку гипотезой являлось существование самих молекул. Достаточно было отрицать их реальность, как это делали Мах, Оствальд и другие, чтобы броуновское движение вновь превратилось в загадку.

У сторонников объяснения броуновского движения на основе теплового движения частиц жидкости, постулируемого молекулярно-кинетической теорией, вскоре нашлись и экспериментальные подтверждения этого. Было установлено, что интенсивность броуновского движения возрастает с увеличением температуры жидкости и с уменьшением массы взвешенных частиц. Постепенно складывалось объяснение явления. В случае большой поверхности взвешенной в жидкости частицы удары молекул о нее, являющиеся причиной движения, не производят никакого действия на взвешенное тело, так как в общем они равномерно толкают тело со всех сторон. При уменьшении массы тела (и, соответственно, его поверхности) удары молекул не уравновешиваются, на частицу со стороны жидкости будет действовать сила, которая по модулю и направлению хаотически меняется. Развитая теория допускала и экспериментальное подтверждение: как только мы докажем совпадение наблюдаемых на опыте отклонений и скоростей броуновских частиц с предсказаниями молекулярно-кинетической теории, мы докажем тем самым и справедливость самой молекулярной теории. Вырисовывались перспективы экспериментального доказательства существования молекул, т. е. подтверждение справедливости дела, которому посвятил всю свою жизнь Людвиг Больцман. Задача состояла теперь в разработке количественной теории броуновского движения.

Первую количественную теорию этого явления создал в 1905 г. А. Эйнштейн. Свой интерес к броуновскому движению он объяснял возможностью проверки справедливости (или ошибочности) молекулярно-кинетической теории. Примечателен подход Эйнштейна к решению задачи. Поскольку все имевшие место до него попытки определения средней скорости движения броуновских частиц были безрезультатны (средняя скорость резко менялась по модулю и направлению, не стремясь к какому-либо пределу при увеличении длительности наблюдений), Эйнштейн выбирает в качестве основной характеристики движения смещение броуновских частиц. Предположив далее, что движение взвешенных частиц полностью хаотично, используя статистику Максвелла — Больцмана, он получил среднее квадратичное смещение частиц вдоль оси x:

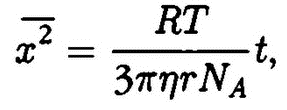
где R — универсальная газовая постоянная, t — время, Т — абсолютная температура, N_A — постоянная Авогадро, ? — коэффициент вязкости, r — радиус броуновской частицы. Поскольку все величины, входящие в эту формулу, определяются экспериментально, из анализа движения броуновских частиц можно вычислить постоянную Авогадро. Сравнение этого значения N_A с данными, полученными из других опытов явилось бы в случае совпадения веским аргументом в пользу справедливости молекулярно-кинетической теории. «Если бы какому-либо исследователю удалось вскоре разрешить поднятые здесь важные для теории теплоты вопросы!» — восклицает Эйнштейн в одной из своих работ.

Прежде всего необходимо было проверить справедливость применения к движению броуновских частиц постулата Эйнштейна о полной хаотичности движения. Идею такой проверки предложил французский физик П. Ланжевен. Для этого надо было расположить в одной точке начало всех смещений броуновских частиц. Если их движение нерегулярно, т. е. подчиняется законам случайности, то концы смещений частиц должны располагаться вокруг их общего центра точно так же, как располагаются при стрельбе вокруг центра мишени попадания пуль. Ж. Перрен выполнил эти исследования. Он проводил в освещенной камере измерения последовательных положений одной и той же броуновской частицы через равные промежутки времени. После 500 измерений он выполнил предлагаемое Ланжевеном геометрическое построение и получил картину, изображенную на рис. 13. Основной постулат Эйнштейна о применимости статистических представлений к анализу движения броуновских частиц получил полное подтверждение. Вслед за этим Перрен и его сотрудники провели вычисления постоянной Авогадро. Рассчитанные ими значения Na совпали со значениями, полученными при использовании других методов, что также подтверждало справедливость теории Эйнштейна. Теперь можно было думать о постановке решающих опытов, называемых experimentum cruris (лат.), доказывающих реальность существования мельчайших структурных единиц материи — молекул и атомов.

^{Рис.13. Положение концов смешений броуновских частиц} 

Эти опыты выполнили в 1906-1908 гг. Ж. Перрен со своими сотрудниками. Идея опытов проста. Анализируя предположения молекулярно-кинетической теории, Перрен пришел к выводу, что ее результаты применимы не только к молекулам жидкости, но и к броуновским частицам, которые можно рассматривать как большие молекулы. При этом распределение броуновских частиц по высоте должно описываться найденной Больцманом барометрической формулой (13) с заменой в ней массы молекул на массу броуновской частицы. Так как броуновские частицы можно непосредственно наблюдать в микроскоп, изучение их распределения по высоте должно было соответствовать этой формуле, т. е. подтвердить или опровергнуть выводы молекулярно-кинетической теории, дать решающие заключения о реальности существования молекул.

^{Рис.14. Уменьшение концентрации броуновских частиц с высотой}

Эксперименты Перрена были весьма трудоемкими и требовали предельной тщательности. Ученый растер в воде желтую краску — гуммигут. Под микроскопом было видно, что в подкрашенной воде находится огромное число желтых шариков различных размеров, твердых и не слипающихся друг с другом. При длительном вращении на центрифуге Перрену удалось отделить порции шариков краски с одинаковыми по размеру зернами. Помещая каплю раствора с зернами гуммигута между двумя горизонтальными стеклами, Перрен наблюдал с помощью микроскопа явное уменьшение взвешенных частиц с высотой, предсказываемое молекулярно-кинетической теорией (см. рис. 8 б). Фокусируя микроскоп на отдельные слои, можно было сфотографировать, а затем подсчитать число частиц в каждом слое. На рис. 14 показаны такие фотографии.

Для выполнения количественных подсчетов Перрен взял четыре слоя, отстоящие друг от друга по вертикали на 5, 35, 65, 95 мкм. Число частиц в слое I, лежащем на высоте h₁, в соответствии с формулой (13) равно

n₁ = n₀ exp (?mgh₁) = п₀ ехр(-3Ph₁/2E),

где Е — средняя кинетическая энергия броуновской частицы, P — ее вес. Аналогично для слоя II получим:

n₂ = п₀ ехр(-3Ph₂/2E).

Из отношения

n₁/n₂ = exp[-³/₂?P(h₁- h₂)/E]

нетрудно получить выражение для определения средней кинетической энергии броуновских частиц:

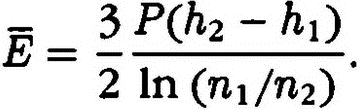
В последнем выражении n₁ и n₂ определяются экспериментально при непосредственном подсчете числа частиц, разность h₂ — h₁ измеряется по сдвигу микрометрического винта микроскопа. Вес броуновских частиц можно определить по формуле

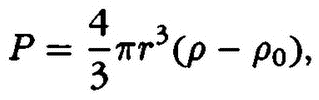
где ?₀ — плотность воды. Радиус частиц r можно получить, измеряя их скорость падения в воде:

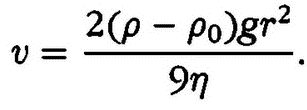
Непосредственно скорость падения отдельных частиц определить нельзя, так как они находятся в хаотическом броуновском движении. Перрен обходит эту трудность следующим способом: эмульсия, налитая в высокий и узкий сосуд, предварительно размешивалась, для того чтобы броуновские частицы распределились в нем равномерно по высоте. Скорость частиц v определялась по скорости оседания границы помутнения. Таким образом были найдены все необходимые для определения г величины, а затем была подсчитана и постоянная Авогадро.

Число зернышек краски в пяти слоях оказалось равным, по данным опытов Перрена, соответственно 100, 47, 22, 6 и 12. Ученый сравнил эти числа с распределением, даваемым формулой Больцмана (13): 100, 46, 23, 11 и 1. Там, где число броуновских частиц было велико (в нижних слоях эмульсии), совпадение теории с экспериментом было полным! Отклонение же числа частиц от теоретического значения при малом числе частиц не должно смущать читателей, ибо согласно законам теории вероятностей именно в области малых чисел отклонения числа частиц от средних значений могут быть значительными (подробнее о теории флуктуации мы поговорим в следующем параграфе).

Повторение опытов с частицами другой природы и другими жидкостями также подтверждали справедливость предсказаний молекулярно-кинетической теории. Эмоциональную атмосферу этих экспериментов передают слова Перрена о том, что он «испытал сильное волнение, когда после первых попыток… получил те же числа, к которым кинетическая теория приходила совершенно другим путем». «Становится весьма трудным отрицать объективную реальность молекул. Атомная теория торжествует, — пишет он в вышедшей в 1912 г. своей монографии “Атомы”, — многочисленные ее противники признают себя побежденными и один за другим отрекаются от того недоверия, которое представлялось им долгие годы законным».

Эксперименты Перрена завершили длившийся со времен Демокрита спор о строении вещества. Читатели этой книги знают, сколь упорным и долгим он был, сколько трудностей ожидало сторонников атомистической теории, независимо от рассматриваемого периода времени. Последней жертвой спора был Л. Больцман. Но эти труды были не напрасны. Они вооружили человечество знанием сокровенных тайн мироздания, дали человечеству ключ к разгадке новых и удивительных тайн природы. После опытов Перрена не признавать атомистику означало идти против очевидных фактов. Один из самых яростных противников атомистики и теории Больцмана В. Оствальд уже в 1908 г. пишет: «Совпадение броуновского движения с требованиями кинетической гипотезы дает право теперь самому осторожному ученому говорить об экспериментальном доказательстве атомистической теории материи. Таким образом, атомистическая теория возведена в ранг научной, прочно обоснованной теории!»

Впрочем, и Э. Мах также вынужден был впоследствии признать существование атомов. Его убедили в этом опыты, когда испускаемые при радиоактивном распаде ?-лучи (позже было установлено, что ими являются двукратно ионизованные атомы гелия He⁺⁺) можно было непосредственно наблюдать, так как при попадании на экран, покрытый сернистым цинком, они вызывали яркую вспышку. Этот прибор получил название спинтарископа. С. Мейер рассказывает: «Одним из самых волнующих воспоминаний останется для меня тот случай, когда Мах после демонстрирования спинтарископа вместо обычных незначительных упрямых возражений скромно заявил: “Теперь я верю в существование атомов”. Так в течение нескольких минут подверглось изменению целое мировоззрение!»

Вместе с признанием реальности существования атомов и молекул резко меняется отношение физиков ко всему созданному Л. Больцманом. Его труды объявляются классическими (рис. 15), а созданная им и другими исследователями кинетическая теория газов перестает быть только теорией газов — она становится кинетической теорией материи! Атомная теория побеждает окончательно. Ее значение для развития науки мне хотелось бы подчеркнуть с помощью слов американского физика-теоретика Р. Фейнмана: «Если бы в результате какой-то мировой катастрофы все накопленные научные знания оказались бы уничтоженными и к грядущим поколениям живых существ перешла бы только одна фраза, то какое утверждение, составленное из наименьшего количества слов, принесло бы наибольшую информацию? Я считаю, что это — атомная гипотеза».

^{Рис. 15. Труды Л. Больцмана}