Вокруг кванта

Опытное доказательство постулатов Бора

Опыт Франка и Герца, по существу, очень похож на опыт Кирхгофа и Бунзена, только атомы натрия в нем они заменили атомами ртути, а вместо луча направили на них пучок электронов, энергию которых они могли менять. При этом Франк и Герц наблюдали интересное явление: пока энергия электронов была произвольной — число электронов, прошедших через атомы ртути, было равно числу электронов исходного пучка. Когда же энергия их достигала определенной величины (в опытах она равнялась 4,9 электрон-вольта, или 7,84 · 10^–12 эрг), число электронов, прошедших ртуть, резко падало — они поглощались атомами ртути. Одновременно с этим в спектре паров ртути вспыхивала яркая фиолетовая линия с длиной волны ? = 2536?, то есть с частотой ? = 1,18 · 10¹⁵ сек^–1. Энергию кванта с такой частотой легко вычислить — она равна E = h? = 6,62 · 10^–27 · 1,2 · 10¹⁵ = 7,82 · 10^–12 эрг, то есть почти точно равна затраченной энергии электрона. Очевидно, это излучение возникает при обратном переходе атома ртути из возбужденного состояния в основное.

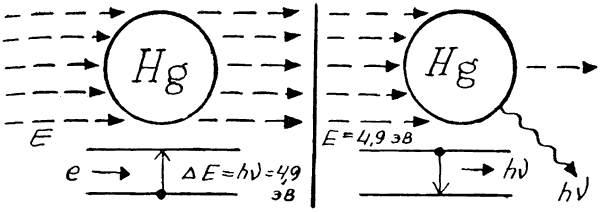
Легко видеть, что наблюдаемая картина — прямое опытное доказательство обоих постулатов Бора: в атоме реально существуют стационарные состояния, и поэтому он не способен поглощать произвольные порции энергии. Переходы электрона между уровнями в атоме возможны только скачками, а частота излучаемых квантов определяется разностью энергий уровней и вычисляется по формуле Эйнштейна ?E = h?. Конечно, «легко видеть» это только сейчас, а в 1913 году даже сами Франк и Герц объяснили свой опыт совсем по-другому.

«Квантование» Солнечной системы

Мы много раз сравнивали атом с солнечной системой, хотя и не придавали глубокого смысла этой аналогии. Тем более неожиданно, что солнечная система, как и атом, тоже подчиняется некоему «правилу квантования». Это правило не имеет ничего общего с квантовой механикой, но тем не менее любопытно, что расстояния планет от Солнца (как и радиусы орбит в атоме) меняются не беспорядочно, а подчиняются довольно строгому закону.

Факт этот был известен Иоганну Кеплеру, и еще в молодости, много размышляя о «гармонии сфер», он пришел к выводу, что в промежутках между сферами, построенными на орбитах планет, можно вписать пять правильных многогранников.

Профессор Даниэль Тициус в 1772 году выпустил в Бонне книгу «Созерцание природы», в которой привел табличку расстояний от Солнца до планет в условных единицах (расстояние до ближайшей к Солнцу планеты Меркурий принято за 4).

Меркурий … 4 = 4;

Венера … 7 = 4 + 1 · 3;

Земля … 10 = 4 + 2 · 3;

Марс … 16 = 4 + 4 · 3;

Юпитер … 52 = 4 + 16 · 3;

Сатурн … 100 = 4 + 32 · 3.

Позднее прибавился

Уран … 196 = 4 + 64 · 3.

Впоследствии Боде уточнил закон Тициуса, приняв расстояние до Меркурия за 8 условных единиц и записав общую формулу для планетных расстояний в виде:

R = 8 + 3 · 2ⁿ,

где n = 0, 1, 2, 3, 4, 6, 7, 8.

Замечательно, что в приведенной схеме нет планеты с номером n = 5, которая должна была бы помещаться между Марсом и Юпитером. Но как раз в этом месте расположен пояс астероидов — малых планет. По мнению астрономов, это осколки некогда существовавшей большой планеты Фаэтон.

Закон Тициуса и Боде еще до конца не понят, хотя существует несколько его доказательств (одно из них принадлежит советскому ученому Отто Юльевичу Шмидту). По-видимому, полное объяснение закону будет найдено вместе с разгадкой происхождения нашей солнечной системы.