3. Кинетическая теория газов
3. Кинетическая теория газов
Очень плодотворным в середине XIX века оказалось представление о молекулярном строении вещества. Когда была принята гипотеза А. Авогадро о том, что в киломоле любого вещества содержится одно и то же количество структурных единиц: 6,02 x 1026 кмоля = 6,02 x 1023 моля, поскольку молярная масса воды M(H2O) = 18 кг/кмоль , следовательно, в 18 литрах воды находится столько же молекул, сколько в 22,4 м3 водяного пара. Это позволяет легко понять, что расстояние между молекулами газообразной воды (пара) значительно больше, в среднем на один порядок, чем в жидкой воде. Можно предположить, что это выполняется для любого вещества. Считая, что в газах молекулы движутся хаотически, можно вывести так называемое основное уравнение кинетической теории:
где Na – 6,02 x 1026 кмоль = 6,02 x 1023 моль – число Авогадро;
VM – молекулярный объем = 22,4 м3;
m – масса одной молекулы;
v – скорость молекулы.
Преобразуем уравнение (4):
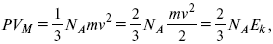
где Ek – энергия одной молекулы.
Видно, что справа стоит полная кинетическая энергия всех молекул. С другой стороны, сравнивая с уравнением Менделеева – Клапейрона, видим, что это произведение равно RT.
Это позволяет выразить среднюю кинетическую энергию молекулы газа:
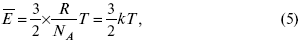
где к = R / Na – постоянная Больцмана, равная 1,38 ґ 10–23 кДж/кмоль. Зная кинетическую энергию молекулы, можно рассчитать ее среднюю скорость
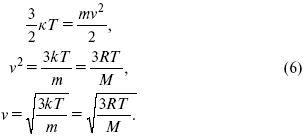
Около 1860 г. Д. К. Максвелл вывел функцию, описывающую распределение молекул газа по скоростям. Эта функция имеет на графике вид характерной кривой с максимумом около наиболее вероятной скорости примерно 500 м/с. Важно заметить, что существуют молекулы со скоростями, превышающими этот максимум. С другой стороны, уравнение (6) позволяет сделать вывод об увеличении доли молекул с большими скоростями при нагревании газа. Спустя почти 60 лет гениальная догадка Д. К. Максвелла была подтверждена в опытах О. Штерна.
Данный текст является ознакомительным фрагментом.