Глава 39 КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
Глава 39
КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
§ 1. Свойства вещества
§ 2. Давление газа
§ 3. Сжимаемость излучения
§ 4. Температура и кинетическая энергия
§ 5. Закон идеального газа
§ 1. Свойства вещества
С этой главы мы начнем изучение новой темы, которая займет у нас довольно много времени. Мы начнем анализ свойств вещества с физической точки зрения. Зная, что вещество построено из большого числа атомов или каких-то других элементарных частей, взаимодействующих электрически и подчиняющихся законам механики, мы постараемся понять, почему скопления атомов ведут себя именно так, а не иначе.
Нечего и говорить, что это трудная задача. И будет лучше, если мы с самого начала подчеркнем, что это чрезвычайно трудная задача и что решать ее нам придется совсем иными способами, чем раньше. Когда мы изучали механику и оптику, то могли начинать с точных формулировок некоторых законов, например законов Ньютона или формулы для поля, порождаемого ускоренным зарядом. Узнав их, мы сразу же могли объяснить бездну всяких явлений, а потом эти законы становились для нас прочной основой, опираясь на которую, мы совершенствовались и в механике, и в оптике. Мы можем продолжать изучение и дальше, но мы не обнаружим при этом какую-то новую физику, мы просто будем решать старые задачи более точными математическими методами.
Такой способ непригоден для изучения свойств вещества. Мы можем сказать о свойствах вещества лишь самые простые вещи. Предмет этот слишком сложен, чтобы можно было начать с самых основных законов. Мы по-прежнему будем пользоваться законами механики и электричества. Но законы эти слишком далеки от тех свойств, которые мы собираемся изучать. От законов Ньютона до свойств вещества очень много шагов и каждый шаг очень труден. Сейчас мы сделаем несколько таких шагов, но мне хочется предупредить вас, что если в предыдущих главах мы анализировали явления более или менее строго, то теперь с каждым шагом мы все больше будем терять строгость. Свойства вещества мы сможем понять лишь весьма приближенно.
Происходит это по нескольким причинам. Во-первых, наш анализ не может быть полным потому, что для этого нужно глубокое знание теории вероятностей; мы ведь не собираемся следить за движением каждого атома, а хотим узнать о среднем числе атомов, движущихся в том или ином направлении, и прикинуть, к чему приведет разница в этих средних. Таким образом, теория вероятностей органически входит в нашу тему, а в математике мы еще не очень сильны и многого от нас не потребуешь.
Вторая и более серьезная причина — чисто физическая. Поведение атомов подчиняется законам не классической, а квантовой механики, и пока мы не изучим квантовую механику, нельзя серьезно говорить об изучении свойств вещества. Речь идет не просто о переходе от больших предметов к маленьким, например от автомобилей к биллиардным шарам, разница между законами классической и квантовой механики гораздо глубже и существенней, и многие объяснения, если исходить из классической механики, будут просто неверными. Так что многих вещей мы пока никак не в состоянии понять, однако мы будем подчеркивать каждый раз, когда объяснения приведут нас в тупик, чтобы по крайней мере хоть предупредить, где он находится. Для этого и говорилось о квантовой механике в предыдущих главах: надо было понять, в каких случаях отказывает механика классическая.
Почему же мы вообще изучаем свойства вещества? Не лучше ли было бы подождать с полгода или год, пока мы не подучим теорию вероятностей и квантовую механику, а потом уж и взяться за свойства вещества поосновательней? На это следует ответить, что трудные вещи лучше изучать не спеша! Сначала мы — плохо ли, хорошо ли — познакомимся с общими идеями, подумаем, что может произойти в тех или иных обстоятельствах, а потом, когда лучше узнаем основные законы, сформулируем все это поточнее.
Каждый, кто хочет всерьез анализировать свойства вещества, должен сначала написать основные уравнения и попытаться решить их. Но каждого, кто начинал с этого, ждала неудача. Успех приходил лишь к тем, кто подходил к делу как физик: у этих людей сначала не было ничего, кроме грубой идеи, а затем они находили верное приближение, соображая, что в этой трудной ситуации можно считать большим, а что малым.
Задачи в этой области столь сложны, что даже не очень четкая и половинчатая идея оправдывает затраченное на нее время, и можно то и дело возвращаться к одной и той же задаче, приближаясь понемногу к ее точному решению. Так мы и поступаем в нашем курсе.
И еще одна причина, по которой мы приступаем сейчас к изучению свойств веществ: нам уже приходилось встречать похожие идеи, например в химии. Некоторые из них известны нам со школы. Было бы интересно понять их с точки зрения физика.
Вот один из самых увлекательных примеров: известно, что равные объемы газов содержат при одинаковом давлении и температуре равное число молекул. Авогадро первым понял закон кратных отношений: из того, что в химической реакции между двумя газами объемы реагирующих газов относятся как целые числа, следует, что равные объемы содержат равное число атомов. Но почему в равных объемах содержится равное число атомов? Можно ли объяснить это, исходя из законов Ньютона? Для этого вам придется изучить эту главу. Мы еще будем впоследствии много говорить о давлениях, объемах, температуре и теплоте.
Мы обнаружим при этом, что многие соотношения между свойствами вещества можно понять, ни слова не говоря об атомах. Например, если какое-нибудь тело сжать, оно нагреется; если тело нагревать, оно начнет расширяться. Связь между этими явлениями можно понять, не изучая строения тела. Занимающаяся такими вещами наука называется термодинамикой. Конечно, глубокое понимание термодинамики возможно лишь после подробного изучения механизма, лежащего в основе того или иного процесса. Вот этим мы и займемся: мы примем с самого начала тот факт, что все вещества состоят из атомов, и постараемся понять свойства вещества и законы термодинамики.
Итак, начнем изучение свойств газов, исходя из законов Ньютона.
§ 2. Давление газа
Каждый знает, что газ оказывает давление. Но отчего? В этом надо разобраться как следует. Если бы наши уши были намного чувствительнее, чем они есть на самом деле, мы бы все время слышали страшный шум. Но природа позаботилась, чтобы наши уши не были столь восприимчивы, ведь они оказались бы для нас совершенно бесполезными — в них постоянно стоял бы дикий гул, похожий на шум от стартующей ракеты. Дело в том, что барабанные перепонки наших ушей соприкасаются с воздухом, а воздух состоит из великого множества беспорядочно движущихся молекул, которые, ударяясь о барабанные перепонки, создают такой шум, как будто сразу очень много барабанщиков отбивают беспорядочную дробь — бум, бум, бум... Однако мы не слышим этих звуков, потому что атомы очень малы, а уши наши недостаточно чувствительны. Беспорядочные удары молекул должны были бы собственно продавить барабанную перепонку, но ее непрестанно бомбардируют и с внутренней стороны, и в результате полная сила, действующая на перепонку, оказывается равной нулю. Если бы откачать воздух с одной стороны или хотя бы сделать разным его относительное количество с обеих сторон, то перепонка продавилась бы в ту или иную сторону, потому что бомбардировка с одной стороны оказалась бы гораздо сильнее. Мы иногда испытываем это неприятное ощущение, когда очень быстро поднимаемся в лифте или на самолете, а хуже всего, если мы еще при этом простужены (в этом случае распухшая слизистая оболочка закрывает каналы, соединяющие через носоглотку внутреннюю полость уха с внешним пространством, и таким образом оба давления не могут быстро уравняться.)
Чтобы проанализировать это явление количественно, предположим, что газ находится в ящике, одна стенка которого представляет собой поршень, способный перемещаться (фиг. 39.1).
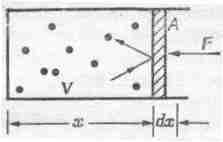
Фиг. 39. 1. Атомы газа в ящике, в котором движется поршень без трения.
Найдем силу, с которой действуют на поршень находящиеся внутри ящика атомы. О поршень ударяются атомы, движущиеся внутри объема V со всевозможными скоростями. Предположим, что вне ящика ничего нет — сплошной вакуум. Что же произойдет? Если предоставить поршень самому себе и не придерживать его, то с каждым ударом молекулы он будет приобретать небольшой импульс и постепенно будет вытолкнут совсем из ящика. Чтобы удержать его в ящике, придется приложить силу F. Какова должна быть эта сила? Говоря о силе, мы будем относить ее к единице площади: если площадь поршня равна А, то действующая на него сила будет пропорциональна площади. Определим давление как величину, равную отношению приложенной к поршню силы к площади поршня:
P =F/A. (39.1)
Чтобы лучше понять, для чего это делается, подсчитаем бесконечно малую работу dW, которую надо затратить, чтобы протолкнуть поршень на бесконечно малое расстояние —dx (позднее это понадобится нам и для других целей); эта работа равна произведению силы на расстояние или, согласно (39.1), произведению давления, площади поршня и расстояния. Все это равно произведению давления на изменение объема, взятого с обратным знаком:
dW=F(-dx)=-PAdx=-PdV. (39.2)
(Произведение площади А на изменение высоты dx равно изменению объема.) Знак минус в этом выражении возникает из-за того, что при сжатии объем уменьшается; если принять это во внимание, то мы получим правильный результат: чтобы сжать газ, надо затратить работу.
Итак, с какой силой надо давить на поршень, чтобы уравновесить удары молекул? При каждом ударе поршню сообщается некий импульс. В каждую секунду поршень получает определенный импульс и начинает двигаться. Чтобы предотвратить это, приложенная нами сила за секунду должна сообщить поршню точно такой же импульс. Таким образом, сила равна импульсу, сообщенному поршню за 1 сек. Можно об этом сказать и иначе: если предоставить поршень самому себе, то он за счет бомбардировки наберет скорость и с каждым ударом будет подталкиваться и двигаться с ускорением. Быстрота изменения скорости поршня, или ускорение, пропорциональна действующей силе. Таким образом, сила, которую мы определили как произведение давления на площадь, равна импульсу, сообщенному поршню за 1 сек всеми молекулами внутри ящика.
Подсчитать импульс, передаваемый поршню за 1 сек, легко; мы сделаем это в два этапа: сначала определим импульс, переданный одним атомом при столкновении с поршнем, а потом умножим эту величину на число соударений атомов с поршнем за 1 сек. Сила и будет произведением этих двух величин.
Займемся теперь этими величинами: предположим сначала, что поршень — это идеальный «отражатель» атомов. Если это не так, то вся наша теория рухнет — поршень начнет нагреваться и произойдет много всяких событий, предсказать которые мы не в состоянии. Однако, когда снова установится равновесие, в результате окажется, что каждое столкновение будет эффективно упругим. В среднем энергия приходящих и уходящих частиц не изменяется. Таким образом, предположим, что газ находится в равновесии и поршень, будучи неподвижным, энергии не поглощает. В этом случае частица, подлетевшая к поршню с определенной скоростью, улетит от него с той же скоростью, причем масса частицы не изменится.
Если v есть скорость атома, a vx— составляющая скорости вдоль оси х, то импульс «к поршню» равен mvx, но раз частица «отражается», то импульс «от поршня» равен той же величине; значит, за одно соударение поршню сообщается импульс 2mvx.
Нужно теперь подсчитать число соударений атома за 1 сек; для этого можно взять любой промежуток времени dt, а потом разделить число соударений на dt. Много ли атомов попадает за это время в цель? Предположим, что в объеме V заключено N атомов, т. е. в каждом единичном объеме имеется n= N/V атомов. Теперь заметим, что за время t достигнут поршня не все частицы, движущиеся к поршню с заданной скоростью, а только те, которые оказались достаточно близко от него. Если частицы были очень далеко, то, хотя они и стремятся к поршню, к сроку они не успеют. Таким образом, за время t о поршень ударятся лишь те частицы, которые в начальный момент были не дальше чем на расстоянии vxt от него. Следовательно, число соударений за время t равно числу атомов, находящихся на расстоянии, не превышающем vxt, а поскольку площадь поршня равна А, то атомы, которые со временем попадут в цель, занимают объем Avxt. А число атомов, попавших в цель, равно произведению объема на число атомов в единичном объеме nvxAt. Но нас, конечно, интересует не число соударений за время t, а мы хотим знать число соударений за 1 сек, поэтому мы делим на t и получаем nvxA. (Время t может быть взято очень малым, для красоты можно писать dt и затем дифференцировать, но это все одно и то же.)
Итак, мы нашли, что сила равна
F=nvxA·2mvx. (39.3)
Обратите внимание, что если фиксировать плотность частиц, то сила оказывается пропорциональной площади! После этого давление найти очень просто:
P=-2nmv2x. (39.4)
Теперь надо исправить кое-какие неточности: прежде всего не все молекулы имеют одну и ту же скорость и не все они движутся в одном направлении, так что нам приходится иметь дело с разными v2x! Каждая молекула, ударяясь о поршень, вносит свой вклад, поэтому надо взять среднее по всем молекулам. Сделав это, мы получим
P=nm<v2x>. (39.5)
А не забыли ли мы множитель 2? Нет, потому что лишь половина атомов движется к поршню. Другие летят в противоположную сторону, а усредняя по v2x, мы усредняем как по положительным, так и по отрицательным составляющим vx.
Если просто усреднить по v2x, получится вдвое больший результат. Среднее v2x для положительных vxравно половине среднего v2x для всех vx.
Но атомы прыгают в ящике как хотят, и поэтому ясно, что x-направление» для них ничем не отличается от любого другого; они движутся куда угодно: вправо — влево, вверх — вниз, взад — вперед. Поэтому <v2x> (средний квадрат скорости движения в одном направлении) равен среднему квадрату скорости в любом другом направлении
<v2x>=<v2y>=<v2z>. (39.6)
Используем это обстоятельство для небольшого математического трюка и обнаружим, что каждый из членов в (39.6) равен их сумме, деленной на три, а сумма — это квадрат величины скорости:
<v2x>=1/3<v2x+v2y+v2z>=<v2>/3. (39.7)
Это очень хорошо, потому что теперь уже не надо заботиться о координатных осях, и формулу для давления можно записать в виде
P=2/3n(mv2/2). (39.8)
Мы выделили множитель <mv2/2>, потому что это кинетическая энергия движения молекулы как целого. Итак, мы нашли
PV=N2/3(mv2/2). (39.9)
Если мы будем знать скорость молекул, то очень быстро подсчитаем давление.
В качестве простого примера можно описать такие газы, как гелий, пары ртути или калия при достаточно высокой температуре или аргон; это одноатомные газы, для которых можно считать, что их атомы не имеют внутренних степеней свободы. Если нам попадется сложная молекула, то в ней могут быть всевозможные внутренние движения, всякого рода колебания и т. д. Мы предполагаем, что можно не принимать их в расчет; но можно ли это делать — вопрос сложный и мы к нему вернемся; в действительности для нашего случая это окажется допустимым. Итак, предположим, что внутреннее движение атомов можно не рассматривать, и поэтому кинетическая энергия движения молекулы как целого восполняет всю энергию. Для одноатомного газа кинетическая энергия — действительно полная энергия. Будем обозначать полную энергию буквой U (иногда ее называют полной внутренней энергией, как-будто у газа может быть какая-то внешняя энергия), т. е. всю энергию всех молекул газа или любого другого объекта.
В случае одноатомного газа мы предположим, что полная энергия U равна произведению числа атомов на среднюю кинетическую энергию каждого из них, потому что мы пренебрегли возможным возбуждением атомов или какими-то внутриатомными движениями. Тогда
PV=2/3U. (39.10)
Немного задержимся и ответим на такой вопрос: предположим, что мы медленно сжимаем газ; каким должно быть давление, чтобы сжать газ до заданного объема? Определить это легко, так как давление есть энергия, деленная на объем. Но когда газ сжимается, производится работа и поэтому энергия газа U возрастает. Процесс сжатия описывается неким дифференциальным уравнением. В начальный момент газ занимает определенный объем и обладает определенной энергией, поэтому нам известно и давление. Как только мы начинаем сжимать газ, энергия U возрастает, объем V уменьшается, а как изменяется давление, нам еще предстоит узнать.
Итак, нам предстоит решить дифференциальное уравнение. Сейчас мы это сделаем. Однако подчеркнем сначала, что, сжимая газ, мы предполагаем, что вся работа уходит на увеличение энергии атомов газа. Вы спросите: «А необходимо ли на этом останавливаться? Куда же еще она может уйти?» Но оказывается, что затраченная работа может уйти и в другое место. Энергия может «вытечь» из ящика сквозь стенки: горячие (т. е. очень быстрые) атомы при бомбардировке будут нагревать стенки ящика и энергия выйдет наружу. Но мы предполагаем, что в нашем случае этого не происходит.
Сделаем небольшое обобщение, хотя и в этом случае мы будем рассматривать лишь очень частный случай: запишем вместо PV=2/3U
PV = (g-1)U. (39.11)
Энергия U умножается на (g-1) для удобства, потому что в дальнейшем нам придется иметь дело с газами, для которых множитель перед U равен не 2/3, а какому-то другому числу. Чтобы можно было описывать и такие случаи, запишем этот множитель так, как его обозначают почти сто лет. Тогда в нашем случае одноатомного газа, такого, как гелий, g=5/з, потому что 5/3-1=2/з.
Мы уже говорили, что совершаемая при сжатии газа работа равна -PdV. Сжатие, при котором тепло не поглощается и не выделяется, называется адиабатическим сжатием; это слово образовано из трех греческих слов: а(не)+dia(сквозь)+bainein(проходить). (Слово адиабатический употребляется в физике в разных смыслах, так что не всегда можно понять, что между ними общего.) При адиабатическом сжатии вся затраченная работа уходит на изменение внутренней энергии. Вот в этом и смысл, что нет потерь энергии и, значит, PdV=-dU. Но поскольку U=PV/g-1, то можно записать
dU=(PdV+VdP)/(g-1). (39.12)
Итак, PdV =-(PdV+VdP)/ (g-1) или, приводя подобные члены, получаем gPdV=-VdP, или
gdv/v+dp/p=0, (39.1З)
Если мы примем, что g постоянна, а это так в случае одноатомных газов, то уравнение интегрируется и мы получаем glnV+lnP=lnC, где С — постоянная интегрирования. Переходя к степеням, мы получаем такой закон:
PVg=C (постоянная). (39.14)
Иначе говоря, если выполнены условия адиабатичности, т. е. потерь энергии нет и газ при сжатии нагревается, то в случае одноатомного газа произведение объема на давление в степени 5/3 есть величина постоянная! Этот результат мы получили чисто теоретически, но опыт показывает, что и в действительности все происходит именно так.
§ 3. Сжимаемость излучения
Приведем еще один пример из кинетической теории газов; он не особенно интересует химиков, но очень важен для астрономов. Внутри нагретого до высокой температуры ящика имеется огромное число фотонов. (В качестве такого ящика надо взять очень горячую звезду. Солнце недостаточно горячо для этих целей. В звезде, правда, слишком много атомов, но если ее температура очень высока, то атомами можно пренебречь и считать, что внутренность звезды целиком заполнена фотонами.) Вспомним теперь, что фотон обладает импульсом р. (При изучении кинетической теории газов мы всегда будем испытывать страшные неудобства: р — это давление, но р — еще и импульс; v — это объем, но это и скорость одновременно, а. Т — это и температура, и кинетическая энергия, и время, и момент силы; тут нужен глаз да глаз.) Сейчас буква р — это импульс, вектор. Поступим так же, как и в предыдущем параграфе, за удары фотонов о стенку ответственна x-составляющая импульса, а удвоенная x-составляющая импульса — это импульс, полученный стенкой после каждого удара. Итак, вместо 2mvxпишем 2рх, а при вычислении числа столкновений нужно по-прежнему подставлять vx; проделав все это, формулу (39.4) для давления мы уже записываем в виде
P=2npxvx. (39.15)
После усреднения мы получим произведение nна среднее значение pxvx(вспомните, что мы говорили о множителе 2), а после того как на помощь будут призваны два других измерения, мы найдем
PV=N<p·v>/3. (39.16)
о
Эта формула почти совпадает с (39.9), потому что импульс равен mv, просто это более общая формула, вот и все. Произведение давления на объем равно произведению полного числа атомов на среднее значение 1/3(p·v).
Чему равно p·v для фотонов? Импульс и скорость направлены одинаково, а скорость равна скорости света, поэтому интересующее нас произведение — это импульс фотона, умноженный на скорость света. Произведение импульса фотона на скорость света — это энергия фотона: Е=рс. Мы имеем дело с энергией каждого фотона и должны умножить среднюю энергию фотона на число фотонов. Получается одна треть полной энергии:
PV=Ui3 (в случае фотонного газа). (39.17)
Для фотонов, следовательно, поскольку впереди стоит 1/3, множитель (g-1) в (39.11) равен l/4, т. е. g= 4/3, значит, излучение в ящике подчиняется закону
РV4/3=С. (39.18)
Таким образом, мы знаем сжимаемость излучения! Можно использовать эту формулу при анализе вклада излучения в давление внутри звезды, подсчитать давление и оценить, как оно изменяется при сжатии звезды. Просто удивительно, как много мы уже умеем!
§ 4. Температура и кинетическая энергия
До сих пор мы не имели дела с температурой; мы сознательно избегали разговоров на эту тему. Мы знаем, что если сжимать газ, энергия молекул возрастает, и мы обычно говорим, что газ при этом нагревается. Теперь надо понять, какое это имеет отношение к температуре. Нам известно, что такое адиабатическое сжатие, а как поставить опыт, чтобы можно было сказать, что он был проведен при постоянной температуре? Если взять два одинаковых ящика с газом, приставить их один к другому и подержать так довольно долго, то даже если вначале эти ящики обладали тем, что мы назвали различной температурой, то в конце концов температуры их станут одинаковыми. Что это означает? Только то, что ящики достигли того состояния, которого они в конце концов достигли бы, если бы их надолго предоставили самим себе! Состояние, в котором температуры двух тел равны — это как раз то окончательное состояние, которого достигают после длительного соприкосновения друг с другом.
Давайте посмотрим, что случится, если ящик разделен на две части движущимся поршнем и каждое отделение заполнено разным газом, как это показано на фиг. 39.2 (для простоты предположим, что имеются два одноатомных газа, скажем, гелий и неон).
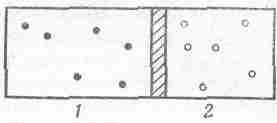
Фиг.39. 2. Атомы двух разных одноатомных газов, разделенных подвижным поршнем.
В отделении 1 атомы массы m1движутся со скоростью v1, а в единице объема их насчитывается n1 штук, в отделении 2 эти числа соответственно равны m2, v2 и n2. При каких же условиях достигается равновесие?
Разумеется, бомбардировка слева заставляет поршень двигаться вправо и сжимает газ во втором отделении, затем то же самое происходит справа и поршень ходит так взад и вперед, пока давление с обеих сторон не сравняется, и тогда поршень остановится. Мы можем устроить так, чтобы давление с обеих сторон было одинаковым, для этого нужно, чтобы внутренние энергии, приходящиеся на единичный объем, были одинаковыми или чтобы произведения числа частиц nв единице объема на среднюю кинетическую энергию было одинаковым в обоих отделениях. Сейчас мы попытаемся доказать, что при равновесии должны быть одинаковы и отдельные сомножители. Пока мы знаем только, что равны между собой произведения чисел частиц в единичных объемах на средние кинетические энергии
это следует из условия равенства давлений и из (39.8). Нам предстоит установить, что по мере постепенного приближения к равновесию, когда температуры газов сравниваются, выполняется не только это условие, а происходит и еще кое-что.
Чтобы было яснее, предположим, что нужное давление слева в ящике достигается за счет очень большой плотности, но малых скоростей. При больших nи малых v можно получить то же самое давление, что и при малых nи больших v. Атомы, если они плотно упакованы, могут двигаться медленно, или атомов может быть совсем немного, но ударяют они о поршень с большей силой. Установится ли равновесие навсегда? Сначала кажется, что поршень никуда не сдвинется и так будет всегда, но если продумать все еще раз, то станет ясно, что мы упустили одну очень важную вещь. Дело в том, что давление на поршень вовсе не равномерное, поршень-то раскачивается точно так же, как барабанная перепонка, о которой мы говорили в начале главы, ведь каждый новый удар не похож на предыдущий. Получается не постоянное равномерное давление, а скорее нечто вроде барабанной дроби — давление непрерывно меняется, и наш поршень как бы постоянно дрожит. Предположим, что атомы правого отделения ударяют о поршень более или менее равномерно, а слева атомов меньше, и удары их редки, но очень энергичны. Тогда поршень то и дело будет получать очень сильный импульс слева и отходить вправо, в сторону более медленных атомов, причем скорость этих атомов будет возрастать. (При столкновении с поршнем каждый атом приобретает или теряет энергию в зависимости от того, в какую сторону движется поршень в момент столкновения.) После нескольких столкновений поршень качнется, потом еще, еще и еще..., газ в правом отделении будет время от времени встряхиваться, а это приведет к увеличению энергии его атомов, и движение их ускорится. Так будет продолжаться до тех пор, пока не уравновесятся качания поршня. А равновесие установится тогда, когда скорость поршня станет такой, что он будет отбирать у атомов энергию так же быстро, как и отдавать. Итак, поршень движется с какой-то средней скоростью, и нам предстоит найти ее. Если нам это удастся, мы подойдем к решению задачи поближе, потому что атомы должны подогнать свои скорости так, чтобы каждый газ получал через поршень ровно столько энергии, сколько теряет.
Очень трудно рассчитать движение поршня во всех деталях; хотя все это очень легко понять, оказывается, что проанализировать это несколько труднее. Прежде чем приступить к такому анализу, решим другую задачу: пусть ящик заполнен молекулами двух сортов с массами m1и m2, скоростями v1и v2 и т. д.; теперь молекулы смогут познакомиться поближе. Если сначала все молекулы № 2 покоятся, то долго это продолжаться не может, потому что о них будут ударять молекулы № 1 и сообщать им какую-то скорость. Если молекулы № 2 могут двигаться значительно быстрее, чем молекулы № 1, то все равно рано или поздно им придется отдать часть своей энергии более медленным молекулам. Таким образом, если ящик заполнен смесью двух газов, то проблема состоит в определении относительной скорости молекул обоих сортов.
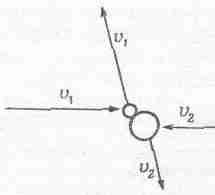
Это тоже очень трудная задача, но мы все-таки решим ее. Сначала нам придется решить «подзадачу» (опять это один из тех случаев, когда, независимо от того как решается задача, окончательный результат запоминается легко, а вывод требует большого искусства). Предположим, что перед нами две сталкивающиеся молекулы, обладающие разными массами; во избежание осложнений мы наблюдаем за столкновением из системы их центра масс (ц. м.), откуда легче уследить за ударом молекул. По законам столкновений, выведенным из законов сохранения импульса и энергии, после столкновения молекулы могут двигаться только так, что каждая сохраняет величину своей первоначальной скорости, и изменить они могут только направление движения. Типичное столкновение выглядит так, как его изобразили на фиг. 39.3.
Фиг. 39. 3. Столкновение двух неодинаковых молекул, если смотреть из системы центра масс.
Предположим на минутку, что мы наблюдаем столкновения, системы центра масс которых покоятся. Кроме того, надо предположить, что все молекулы движутся горизонтально. Конечно, после первого же столкновения часть молекул будет двигаться уже под каким-то углом к исходному направлению. Иначе говоря, если вначале все молекулы двигались горизонтально, то спустя некоторое время мы обнаружим уже вертикально движущиеся молекулы. После ряда других столкновений они снова изменят направление и повернутся еще на какой-то угол. Таким образом, если кому-нибудь и удастся сначала навести порядок среди молекул, то все равно они очень скоро разбредутся по разным направлениям и с каждым разом будут все больше и больше распыляться. К чему же это в конце концов приведет? Ответ: Любая пара молекул будет двигаться в произвольно выбранном направлении столь же охотно, как и в любом другом. После этого дальнейшие столкновения уже не смогут изменить распределения молекул.
Что имеется в виду, когда говорят о равновероятном движении в любом направлении? Конечно, нельзя говорить о вероятности движения вдоль заданной прямой — прямая слишком тонка, чтобы к ней можно было относить вероятность, а следует взять единицу «чего-нибудь». Идея заключается в том, что через заданный участок сферы с центром в точке столкновения проходит столько же молекул, сколько через любой другой участок сферы. В результате столкновений молекулы распределяются по направлениям так, что любым двум равным по площади участкам сферы будут соответствовать равные вероятности (т. е. одинаковое число прошедших через эти участки молекул).
Между прочим, если мы будем сравнивать первоначальное направление и направление, образующее с ним какой-то угол 0, то интересно, что элементарная площадь на сфере единичного радиуса равна произведению 2p на sinqdq, или, что то же самое, на дифференциал cosq. Это означает, что косинус угла 9 между двумя направлениями с равной вероятностью принимает любое значение между -1 и +1.
Теперь нам надо вспомнить о том, что имеется на самом деле; ведь у нас нет столкновений в системе центра масс, а сталкиваются два атома с произвольными векторными скоростями v1 и v2. Что происходит с ними? Мы поступим так: снова перейдем к системе центра масс, только теперь она движется с «усредненной по массам» скоростью vц.м.=(m1v1+m2v2)/(m1+m2). Если следить за столкновением из системы центра масс, то оно будет выглядеть так, как это изображено на фиг. 39.3, только надо подумать об относительной скорости столкновения w. Относительная скорость равна v1-v2. Дело, следовательно, обстоит так: движется система центра масс, а в системе центра масс молекулы сближаются с относительной скоростью w; столкнувшись, они движутся по новым направлениям. Пока все это происходит, центр масс все время движется с одной и той же скоростью без изменений.
Ну и что же получится в конце концов? Из предыдущих рассуждений делаем следующий вывод: при равновесии все направления, w равновероятны относительно направления движения центра масс. Это означает, что в конце концов не будет никакой корреляции между направлением относительной скорости и движением центра масс. Если бы даже такая корреляция существовала вначале, то столкновения ее бы разрушили и она в конце концов исчезла бы полностью. Поэтому среднее значение косинуса угла между w и vц.м. равно нулю. Это значит, что
<w·vц.м.>=0. (39.19)
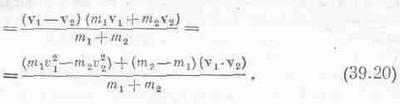
Скалярное произведение w·vц.м. легко выразить через v1 и v2:
Займемся сначала v1·v2; чему равно среднее v1·v2? Иначе говоря, чему равно среднее проекции скорости одной молекулы на направление скорости другой молекулы? Ясно, что вероятности движения молекулы как в одну сторону, так и в противоположную одинаковы. Среднее значение скорости v2 в любом направлении равно нулю. Поэтому и в направлении v1 среднее значение v2 тоже равно нулю. Итак, среднее значение v1·v2 равно нулю! Следовательно, мы пришли к выводу, что среднее т1v21должно быть равно т2v22. Это значит, что средние кинетические энергии обеих молекул должны быть равны:
1/2m1v21=1/2m2v22. (39.21)
Если газ состоит из атомов двух сортов, то можно показать (и мы даже считаем, что нам удалось это сделать), что средние кинетические энергии атомов каждого сорта равны, когда газ находится в состоянии равновесия. Это означает, что тяжелые атомы движутся медленнее, чем легкие; это легко проверить, поставив эксперимент с «атомами» различных масс в воздушном желобе.
Теперь сделаем следующий шаг и покажем, что если в ящике имеются два газа, разделенные перегородкой, то по мере достижения равновесия средние кинетические энергии атомов разных газов будут одинаковы, хотя атомы и заключены в разные ящики. Рассуждение можно построить по-разному. Например, можно представить, что в перегородке проделана маленькая дырочка (фиг. 39.4), так что молекулы одного газа проходят сквозь нее, а молекулы второго слишком велики и не пролезают.
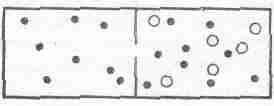
Фиг. 39. 4. Два газа в ящике, разделенном полупроницаемой перегородкой.
Когда установится равновесие, то в том отделении, где находится смесь газов, средние кинетические энергии молекул каждого сорта сравняются. Но ведь в числе проникших сквозь дырочку молекул есть и такие, которые не потеряли при этом энергии, поэтому средняя кинетическая энергия молекул чистого газа должна быть равна средней кинетической энергии молекул смеси. Это не очень удовлетворительное доказательство, потому что ведь могло и не быть такой дырочки, сквозь которую пройдут молекулы одного газа и не смогут пройти молекулы другого.
Давайте вернемся к задаче о поршне. Можно показать, что кинетическая энергия поршня тоже должна быть равна 1/2m2v22. Фактически кинетическая энергия поршня связана только с его горизонтальным движением. Пренебрегая возможным движением поршня вверх и вниз, мы найдем, что горизонтальному движению соответствует кинетическая энергия 1/2m2v22x. Но точно так же, исходя из равновесия на другой стороне, можно показать, что кинетическая энергия поршня должна быть равна 1/2т1v21x. Хотя мы повторяем предыдущее рассуждение, возникают некоторые дополнительные трудности в связи с тем, что в результате столкновений средние кинетические энергии поршня и молекулы газа сравниваются, потому что поршень находится не внутри газа, а смещен в одну сторону.
Если вас не удовлетворит и это доказательство, то можно придумать искусственный пример, когда равновесие обеспечивается устройством, по которому молекулы каждого газа бьют с обеих сторон. Предположим, что сквозь поршень проходит короткий стержень, на концах которого насажено по шару. Стержень может двигаться сквозь поршень без трения. По каждому из шаров со всех сторон бьют молекулы одного сорта. Пусть масса нашего устройства равна m, а массы молекул газа, как и раньше, равны m1и m2. В результате столкновений с молекулами первого сорта кинетическая энергия тела массы mравна среднему значению 1/2 mtv21(мы уже доказали это). Точно так же, столкновения с молекулами второго сорта заставляют тело иметь кинетическую энергию, равную среднему значению 1/2mzv22. Если газы находятся в тепловом равновесии, то кинетические энергии обоих шаров должны быть равны. Таким образом, результат, доказанный для случая смеси газов, можно немедленно обобщить на случай двух разных газов при одинаковой температуре.
Итак, если два газа имеют одинаковую температуру, то средние кинетические энергии молекул этих газов в системе центра масс равны.
Средняя кинетическая энергия молекул — это свойство только «температуры». А будучи свойством «температуры», а не газа, она может служить определением температуры. Средняя кинетическая энергия молекулы, таким образом, есть некоторая функция температуры. Но кто нам подскажет, по какой шкале отсчитывать температуру? Мы можем сами определить шкалу температуры так, что средняя энергия будет пропорциональна температуре. Лучше всего для этого назвать «температурой» саму среднюю энергию. Это была бы самая простая функция, но, к несчастью, эту шкалу уже выбрали иначе и вместо того, чтобы назвать энергию молекулы просто «температурой», используют постоянный множитель, связывающий среднюю энергию молекулы и градус абсолютной температуры, или градус Кельвина. Этот множитель: k=1,38·10-23 дж на каждый градус Кельвина. Таким образом, если абсолютная температура газа равна Т, то средняя кинетическая энергия молекулы равна 3/2kT (множитель 3/2 введен только для удобства, благодаря чему исчезнут множители в других формулах).
Заметим, что кинетическая энергия, связанная с составляющей движения в любом направлении, равна только 1/2kТ. Три независимых направления движения доводят ее до 3/2kT.
§ 5. Закон идеального газа
Теперь можно подставить наше определение температуры в уравнение (39.9) и найти закон зависимости давления газа от температуры: произведение давления на объем равно произведению полного числа атомов на универсальную постоянную k и температуру:
PV=NkT. (39.22)
Следовательно, при одинаковых температуре, давлении и объеме число атомов строго определено — это тоже универсальная постоянная! Таким образом, из законов Ньютона следует, что в равных объемах любых газов при одинаковых температуре и давлении содержится равное число молекул. Вот какой неожиданный вывод!
На практике, когда имеешь дело с молекулами, приходится оперировать большими числами, поэтому химики произвольно выбрали число, очень большое число, и придумали ему специальное название. Они назвали его моль. Моль — это очень искусственное число. Почему химики не приняли за единицу 1024, чтобы вышло круглое число,— это вопрос исторический.
Случилось так, что они для удобства выбрали стандартное число N0=6,02·1023 объектов и назвали это число молем объектов. После этого, вместо того чтобы измерять число молекул в штуках, они измеряют их в молях. Можно написать число молей (выражая их через N0) и умножить его на число атомов в моле, потом умножить на kT, а затем, если захотим, выделить произведение числа атомов в моле на k, тогда получится молярное значение k; для этой величины выделим особую букву R. Молярное значение k равно 8,317 дж: R=N0k=8,317дж/молъ·°К-1. Таким образом мы нашли газовый закон, выраженный в виде произведения числа молей (его обозначают буквой N) на RT, или в виде произведения числа атомов на kT:
PV=NRT. (39.23)
Смысл тот же самый, только единицы измерения разные. В качестве единицы мы используем 1, а химики используют 6·1023!
Сделаем еще одно замечание по поводу газового закона; оно касается вещей более сложных, чем одноатомные молекулы. Пока мы имели дело только с движением одноатомного газа в центре масс. А что если при этом учесть действие сил? Рассмотрим сначала случай, когда поршень удерживается горизонтально расположенной пружинкой, на которую действует сила. Взаимная встряска атомов и поршня в каждый данный момент, конечно, не зависит от положения поршня. Условия равновесия остаются прежними. Независимо от того, где находится поршень, от него требуется только, чтобы скорость его движения была такой, чтобы он получал от молекул столько же энергии, сколько отдавал им. Наличие пружинки не меняет дела. Скорость, с которой движется поршень, в среднем та же. Таким образом, наша теорема о том, что средняя кинетическая энергия в одном направлении равна 1/2kT, справедлива независимо от того, есть силы или их нет.
Рассмотрим, например, двухатомную молекулу, составленную из атомов с массами mАи mB. Нам удалось доказать, что движение в центре масс части А и части В таково, что <1/2mAv2A>=<1/2mBv2B> = 3/2kT. Но как это может быть, если отдельные части связаны друг с другом? Хотя они и связаны между собой, но обмен энергией при взаимных вращениях, изменении расстояния и соударениях с другими молекулами зависит только от того, как быстро они движутся. Только этим определяется обмен энергией при соударениях. Сила в каждый отдельный момент не имеет никакого значения. Следовательно, даже если между отдельными частями молекулы действуют силы, верен тот же принцип.
Докажем, наконец, что газовый закон справедлив и в том случае, когда внутреннее движение не учитывается. До сих пор нам не надо было включать внутреннее движение. Мы просто рассматривали одноатомный газ. Но теперь мы покажем, что скорость центра масс любого объекта, который можно рассматривать как тело массы М, равна
1/2Mv2ц..м.=3/2kT. (39.24)
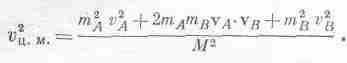
Иначе говоря, можно рассматривать как отдельные части, так и всю молекулу в целом! Посмотрим, почему это можно делать: масса двухатомной молекулы равна М=mА+mB, а скорость центра масс равна vц.м. =(mAvA+mBvB)/M. Нам нужно теперь определить <v2ц.м.>. Если возвести в квадрат vц.м., то получится
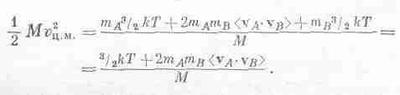
Умножив это на 1I2M и усреднив, получим
[Мы воспользовались тем, что (mA+mB)/М=1.] А чему равно <vA·vB>? (Хорошо бы, чтобы это было равно нулю!) Чтобы найти это среднее, используем наше предположение, что относительная скорость w=vA-vb не предпочитает какое-то одно определенное направление остальным, т. е. средняя составляющая вдоль любого направления равна нулю. Мы предполагаем, следовательно, что
<w·vц.м.>=0.
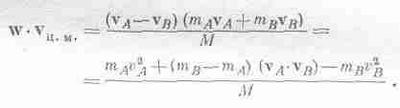
Но что такое w·vц.м.? Это скалярное произведение, равное
Далее, поскольку <,mAv2A>= <mBv2B>, то первый и последний члены взаимно уничтожаются, и мы получаем
(mB-mA)<vA·vB>=0.
Итак, если mА№mB, то <va·vв>=0, а это означает, что жесткому движению всей молекулы, рассматриваемой как одна частица массы М, соответствует средняя кинетическая энергия, равная 3/2kT.
Одновременно мы доказали, что средняя кинетическая энергия внутреннего движения двухатомной молекулы, если не учитывать движения центра масс, равна 3/2kT! Ведь полная кинетическая энергия отдельных частей молекулы равна 1/2mAv2A+1/2mBv2B, а среднее ее значение — это 3/2kT+3/2kT, или 3kT. Кинетическая энергия движения центра масс равна 3/2kT, так что средняя кинетическая энергия вращательного и колебательного движений двух атомов внутри молекулы — это разность этих величин, 3/zkT.
Теорема о средней энергии центра масс — это весьма общая теорема: для каждого объекта, рассматриваемого как единое целое, независимо от того, действуют на этот объект силы или нет, средняя кинетическая энергия каждого независимого движения равна 1l2kT. Эти «независимые направления движения» иногда называют степенями свободы системы. Число степеней свободы молекулы, составленной из rатомов, равно 3r, потому что для определения положения каждого атома нужны три координаты. Полную кинетическую энергию молекулы можно представить либо как сумму кинетических энергий отдельных атомов, либо как сумму кинетической энергии движения Центра масс и кинетической энергии внутренних движений. Последнюю иногда можно представить как сумму кинетической энергии вращений и кинетической энергии колебаний, но это можно сделать только приближенно. Наша теорема, если применить ее к r-атомной молекуле, гласит, что средняя кинетическая энергия молекулы равна 3/2rkT дж, из которых 3/2kT — кинетическая энергия движения молекулы как целого, а остаток 3/2(r-1)kT — это внутренняя кинетическая энергия вращений и колебаний.
* Стоградусная шкала— это шкала Кельвина, в которой за нуль принята температура 273,16°, так что T=273,16+стоградусная температура.
** То, что химики называют молекулярным весом, есть не что иное, как масса моля молекул в граммах. Моль определяется так, что масса моля атомов изотопа углерода 12 (ядра которого состоят из 6 протонов и 6 нейтронов) равна в точности 12 г.
* Этот аргумент, который приводил еще Максвелл, несколько коварен. Хотя окончательный вывод и справедлив, но он не следует непосредственно из соображений симметрии, которыми мы пользовались раньше. Ведь перейдя к движущейся через газ системе отсчета, мы можем обнаружить искаженное распределение скоростей. Мы не смогли найти простого доказательства этого результата.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
2. Кинетическая теория газов. Статистическая механика
2. Кинетическая теория газов. Статистическая механика Если все материальные тела состоят из атомов, то естественно допустить, что в телах, находящихся в газообразном состоянии, частицы в среднем находятся достаточно далеко друг от друга и большую часть времени двигаются
Кинетическая теория вещества
Кинетическая теория вещества Возможно ли объяснить тепловые явления в терминах, относящихся к движению частиц, взаимодействующих между собой с помощью простых сил? Пусть замкнутый сосуд содержит определенную массу газа, например воздуха, при определенной температуре.
Глава 1. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
Глава 1. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ Какими бы ни были воспоминания о школьных годах, в них всегда есть одна общая деталь: в каждом классе всегда находилась горстка детей — самых «крутых», — пылающих неутолимой страстью высмеивать все и вся вокруг. Вот почему
РАБОТЫ БЕРНУЛЛИ И ЭЙЛЕРА ПО МЕХАНИКЕ ЖИДКОСТЕЙ И ГАЗОВ
РАБОТЫ БЕРНУЛЛИ И ЭЙЛЕРА ПО МЕХАНИКЕ ЖИДКОСТЕЙ И ГАЗОВ Проблема взаимодействия между жидкостью и частично или полностью погруженным в нее телом возникла из нужд практики в древности. Еще Архимед открыл закон, выражающий подъемную силу, которая поддерживает плавающее
3. Кинетическая теория газов
3. Кинетическая теория газов Очень плодотворным в середине XIX века оказалось представление о молекулярном строении вещества. Когда была принята гипотеза А. Авогадро о том, что в киломоле любого вещества содержится одно и то же количество структурных единиц: 6,02 x 1026 кмоля =
3. Растворимость газов в жидкостях
3. Растворимость газов в жидкостях Она зависит от давления и температуры. Растворимость газов неодинакова из-за различной химической природы.Пример:N2, H2 – мало растворимы в воде, растворимость NH3, HCl очень велика, в одном объеме H2O растворяется 700 объемов аммиака NH3.Газ + H2O ?
Глава 5 Специальная теория относительности
Глава 5 Специальная теория относительности Установив исходные факты, мы начнем строить, основываясь на них, нашу теорию и попытаемся определить, какие моменты в данном деле можно считать узловыми. Конан Дойль «Записки Шерлока Холмса» Принципы построения Попытки решить
Глава 6 Общая теория относительности
Глава 6 Общая теория относительности Каждый из магов имеет свой предел… [они] могут, скажем, останавливать время, но только в римановом пространстве и ненадолго. Аркадий Стругацкий, Борис Стругацкий «Понедельник начинается в субботу» Предпосылки построения ОТО Наконец,
СЖИЖЕНИЕ ГАЗОВ
СЖИЖЕНИЕ ГАЗОВ Вернемся на несколько лет назад, в 1823 год, когда, используя сжатие и охлаждение, Фарадей смог добиться сжижения различных газов — хлора, диоксида водорода, сульфгидрильной кислоты — и опубликовал первое серьезное исследование по сжижению газов, что было
Глава 1 Специальная теория относительности
Глава 1 Специальная теория относительности Что будет, если посмотреть на себя в зеркало, когда путешествуешь со скоростью света? Какими бы ни были воспоминания о школьных годах, в них всегда есть одна общая деталь: в каждом классе всегда находилась горстка детей – самых