Глава 22 О теории пульсаров
Глава 22 О теории пульсаров
После того как в предыдущих параграфах было рассказано об основных наблюдательных фактах, касающихся пульсаров, уместно перейти к обсуждению существующих теорий. В какой-то степени мы уже осветили раньше теоретический аспект проблемы пульсаров, когда обсуждалось их отождествление с быстро вращающимися нейтронными звездами. Несомненно, что это отождествление является выдающимся достижением современной астрономии. Но, конечно, мало доказать, что пульсары — это быстро вращающиеся нейтронные звезды. Необходимо понять причину их фантастически мощного электромагнитного излучения. Этот вопрос имеет принципиальное значение. Хотя феномен нейтронной звезды теоретически известен астрономам вот уже 40 лет, полной неожиданностью оказалась невероятно высокая активность этих объектов.
В § 19 уже говорилось, что спустя свыше 30 лет после теоретического обоснования необходимости существования нейтронных звезд и незадолго до открытия пульсаров Пиддингтон, Кардашев и вслед за ними Пачини пришли к выводу, что нейтронные звезды должны быстро вращаться и быть сильно намагниченными. Но каким же образом все-таки излучает радиоволны такой объект? Этот вопрос оказался далеко не простым. Надо прямо сказать, что на сегодняшний день не существует общепризнанной количественной теории радиоизлучения пульсаров. Сказанное не означает, что теоретики за 15 лет открытия пульсаров ничего не сделали в этой области. Несомненно, продвижение есть, и многое в какой-то степени прояснилось. Но задача эта на самом деле оказалась исключительно трудной. Слишком «экстремальны» физические условия в пульсарах. Их, например, невозможно в настоящее время моделировать в лабораторных условиях. Чудовищно высокая напряженность магнитного поля, о чем уже речь шла выше, радикально меняет картину распространения радиоволн в плазме. Наконец, большой теоретической проблемой является понимание структуры физических условий недр нейтронной звезды. Грубая модель обсуждалась выше. Но очень важно и вместе с тем необычайно трудно понять причину «звездотрясений», да и вращение сверхтекучего тела вокруг своей оси ставит немало проблем. Ведь из-за отсутствия вязкости и «сцепления» между частицами такое вещество, казалось бы, не должно вращаться как твердое тело...
Итак, нерешенных проблем в физике нейтронных звезд более чем достаточно. Поэтому, освещая современное состояние теории пульсаров, мы будем останавливаться только на самых простых и хорошо апробированных положениях. Заметим, однако, что даже и здесь отсутствует единство взглядов ученых и однозначность в истолковании результатов наблюдений.
Прежде всего следует сказать хотя бы несколько слов об ожидаемых теоретических свойствах нейтронных звезд. Сама возможность существования нейтронных звезд как стабильных конфигураций, находящихся в состоянии равновесия под действием сил гравитации и давления, была высказана еще в 1934 г. американскими астрономами Цвикки и Бааде, которые предположили, что нейтронные звезды образуются при вспышках сверхновых звезд. Долгие годы после этого было совершенно не ясно, образуются ли действительно нейтронные звезды или они представляют собой только изящную математическую конструкцию. Между тем теоретики продолжали исследовать сверхплотное состояние звездного вещества. Уже давно стало ясно, что гипотетические нейтронные звезды не могут представлять собой однородной конфигурации, другими словами, физическое состояние нейтронной звезды должно меняться от ее периферии к центру. Нельзя также считать, что вещество такой звезды состоит только из очень плотно упакованных нейтронов. Во всей ее толще в качестве «примеси» к нейтронам должны быть протоны и электроны. Вблизи поверхности должны доминировать тяжелые ядра, а в самых центральных областях — сверхтяжелые элементарные частицы — гипероны, которые в условиях лабораторных экспериментов крайне нестабильны. Выяснилось, что эти ядра в наружных слоях нейтронной звезды должны образовывать кристаллическую решетку, т. е. периферия нейтронной звезды представляет собой твердое тело. Между тем внутренние ее слои должны представлять собой сверхтекучую жидкость.
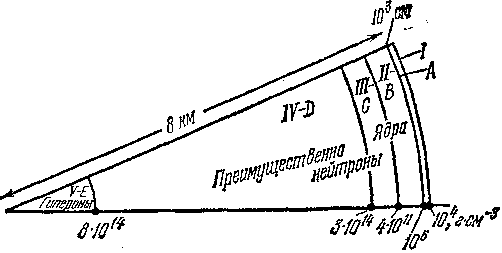 Рис. 22.1: Схема внутреннего строения нейтронной звезды.
Рис. 22.1: Схема внутреннего строения нейтронной звезды.
Следует подчеркнуть, что при построении модели нейтронной звезды теоретики столкнулись с большими трудностями, связанными главным образом с недостаточностью наших знаний о природе ядерных сил, действующих между частицами, образующими нейтронную звезду. Тем не менее «полукачественную» модель нейтронной звезды все же удалось построить. На рис. 22.1 схематически показана стратификация вещества в нейтронной звезде, как она представляется в настоящее время. Вблизи поверхности вещество состоит главным образом из очень плотно «упакованных» ядер железа. Кроме того, там имеется сравнительно небольшое количество ядер гелия и других легких элементов, а также очень плотный вырожденный электронный газ, подобный тому, какой имеется в недрах белых карликов (см. § 10). Присутствие электронов необходимо для компенсации положительного объемного заряда ядер. По мере продвижения в глубь нейтронной звезды ее плотность растет и электроны как бы «вдавливаются» в ядра. При этом образуются богатые нейтронами ядра, более тяжелые, чем ядра железа. При плотности вещества около 3
 1011 г/см3 эти тяжелые ядра перестают быть устойчивыми. Они начинают выбрасывать нейтроны и постепенно по мере продвижения в глубь вещество становится смесью очень плотно упакованных нейтронов, в то время как тяжелые ядра уже играют роль сравнительно небольшой «примеси». Наконец, при плотности около 5
1011 г/см3 эти тяжелые ядра перестают быть устойчивыми. Они начинают выбрасывать нейтроны и постепенно по мере продвижения в глубь вещество становится смесью очень плотно упакованных нейтронов, в то время как тяжелые ядра уже играют роль сравнительно небольшой «примеси». Наконец, при плотности около 5
 1013 г/см3 тяжелые ядра совсем исчезают. При больших плотностях, уже приближающихся к ядерной плотности, вещество состоит преимущественно из очень плотно упакованных нейтронов со сравнительно небольшой примесью протонов и электронов. При плотности
1013 г/см3 тяжелые ядра совсем исчезают. При больших плотностях, уже приближающихся к ядерной плотности, вещество состоит преимущественно из очень плотно упакованных нейтронов со сравнительно небольшой примесью протонов и электронов. При плотности
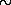 3
3
 1014 г/см3 концентрация заряженных элементарных частиц — протонов и электронов — составляет еще несколько процентов от концентрации нейтронов. Наконец, в самых центральных областях нейтронной звезды появляются и начинают играть существенную роль гипероны (прежде всего сигма-минус-гипероны, обозначаемые символом
1014 г/см3 концентрация заряженных элементарных частиц — протонов и электронов — составляет еще несколько процентов от концентрации нейтронов. Наконец, в самых центральных областях нейтронной звезды появляются и начинают играть существенную роль гипероны (прежде всего сигма-минус-гипероны, обозначаемые символом
 -), а также мю-мезоны, которые вместе с нейтронами, электронами и протонами являются там доминирующими частицами. Не исключено, что в самых центральных областях нейтронной звезды вещество состоит из очень плотно упакованных кварков. Следует, однако, подчеркнуть, что физические условия в самых центральных областях нейтронной звезды известны сейчас особенно плохо. Слишком еще несовершенны наши знания о характере взаимодействия этих частиц в столь необычных условиях.
-), а также мю-мезоны, которые вместе с нейтронами, электронами и протонами являются там доминирующими частицами. Не исключено, что в самых центральных областях нейтронной звезды вещество состоит из очень плотно упакованных кварков. Следует, однако, подчеркнуть, что физические условия в самых центральных областях нейтронной звезды известны сейчас особенно плохо. Слишком еще несовершенны наши знания о характере взаимодействия этих частиц в столь необычных условиях.
Недостаточность знаний физических условий в самых центральных областях нейтронных звезд делает пока далекими от совершенства их модели, т. е. построение теоретической зависимости радиусов нейтронных звезд от их массы. Тем не менее кое-какие результаты теоретиками уже получены. Например, оказалось, что чем меньше масса нейтронной звезды, тем больше ее радиус.
В этой связи следует подчеркнуть, что теория еще не может указать на область допустимых значений масс нейтронных звезд, хотя большая часть специалистов полагает, что массы их должны быть сравнительно невелики, в пределах 0,15
 1,5M
1,5M
 . Этот важный вопрос пока еще далек от ясности.
. Этот важный вопрос пока еще далек от ясности.
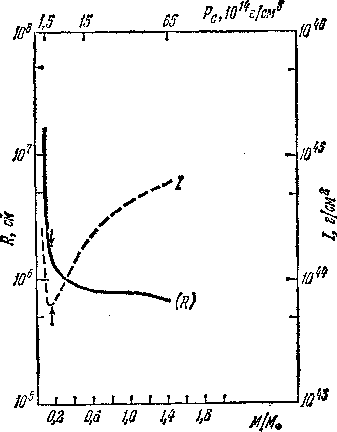 Рис. 22.2: Теоретическая зависимость радиуса и момента инерции нейтронных звезд от их массы.
Рис. 22.2: Теоретическая зависимость радиуса и момента инерции нейтронных звезд от их массы.
На рис. 22.2 приведена од на из существующих моделей нейтронных звезд, дающая зависимость их радиуса от массы. Для масс больших, чем 1M
 , разные модели дают разные зависимости R(M), что объясняется незнанием точного уравнения состояния вещества для плотности, превышающей 1015 г/см3 (сравните с зависимостью «масса — радиус» для белых карликов на рис. 10.1).
, разные модели дают разные зависимости R(M), что объясняется незнанием точного уравнения состояния вещества для плотности, превышающей 1015 г/см3 (сравните с зависимостью «масса — радиус» для белых карликов на рис. 10.1).
Большой интерес представляют уже упоминавшиеся в предыдущем параграфе «звездотрясения», т. е. скачки в периоде пульсаров PSR 0831—45 (Паруса X) и NP 0531 (Краб). У первого пульсара наблюдались два таких скачка, разделенных промежутком времени больше двух лет, причем относительное изменение периода достигало 10-6. У NP 0531 такие скачки значительно меньше. Вероятнее всего «звездотрясения» связаны со скачкообразным изменением момента инерции вращающейся нейтронной звезды. Такое изменение может быть достигнуто, если нейтронная звезда уменьшает свой радиус на величину
 0,01 см. Как можно понять такое явление?
0,01 см. Как можно понять такое явление?
Из-за быстрого вращения равновесной конфигурацией нейтронной звезды должна быть фигура, близкая к эллипсоиду вращения. Но вследствие непрерывного замедления вращения должны меняться параметры этого эллипсоида (он должен становиться все менее сплюснутым). Однако жесткость твердой «коры» нейтронной звезды препятствует «плавному» изменению ее фигуры. По этой причине в коре накапливаются упругие натяжения, и после достижения предела прочности происходит скачкообразная деформация коры, носящая характер сдвига. Таким образом, изучение «звездотрясений» позволяет глубже понять свойства нейтронных звезд.
На рис. 22.2 приведена также теоретически рассчитанная характеристика нейтронной звезды — ее момент инерции I, определяющий кинетическую энергию вращения (E =
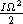 , где
, где
 — угловая скорость). Для допустимых значений массы нейтронных звезд (0,15 < M < 1
— угловая скорость). Для допустимых значений массы нейтронных звезд (0,15 < M < 1
 2M
2M
 ) 7
) 7
 1043 < I < 7
1043 < I < 7
 1044 г/см2.
1044 г/см2.
Из наблюдаемого увеличения периодов пульсаров со временем можно получить
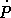 , а следовательно, и
, а следовательно, и
 =
=
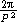
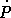 .
.
Скорость уменьшения кинетической энергии вращения пульсара
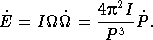 (22.1)
(22.1)
Первая задача физики пульсаров — понять, почему вращающиеся нейтронные звезды тормозятся, тем самым непрерывно выделяя энергию. Простейшее объяснение этого явления сводится к тому, что нейтронные звезды сильно намагничены. Тогда вращающаяся нейтронная звезда, находящаяся в вакууме, будет излучать магнитно-дипольное излучение, частота которого равна частоте вращения, а мощность определяется формулой
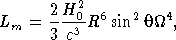 (22.2)
(22.2)
где
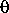 — угол между магнитной осью и осью вращения, H0 — напряженность магнитного поля на поверхности пульсара. Например, пульсар в Крабовидной туманности NP 0531, для которого
— угол между магнитной осью и осью вращения, H0 — напряженность магнитного поля на поверхности пульсара. Например, пульсар в Крабовидной туманности NP 0531, для которого
 = 200 с-1,
= 200 с-1,
 = 2,4
= 2,4
 10-9, теряет энергию
10-9, теряет энергию
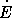 = 3
= 3
 1038 эрг/с. Если причина торможения — магнитно-дипольное излучение, то, приравнивая
1038 эрг/с. Если причина торможения — магнитно-дипольное излучение, то, приравнивая
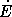 = Lm, найдем, что H0
= Lm, найдем, что H0
 3
3
 1012 Э. Другой причиной торможения этого пульсара может быть излучение им гравитационных волн (см. § 24). Для этого надо только предположить, что фигура нейтронной звезды слегка асимметрична, т. е. представляет собой трехосный эллипсоид. В этом случае мощность гравитационного излучения вращающейся нейтронной звезды определяется формулой
1012 Э. Другой причиной торможения этого пульсара может быть излучение им гравитационных волн (см. § 24). Для этого надо только предположить, что фигура нейтронной звезды слегка асимметрична, т. е. представляет собой трехосный эллипсоид. В этом случае мощность гравитационного излучения вращающейся нейтронной звезды определяется формулой
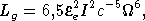 (22.3)
(22.3)
где I — момент инерции, а
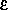 e — эксцентриситет экваториального эллипса нейтронной звезды. Частота гравитационных волн, как оказывается, равна удвоенной частоте вращения.
e — эксцентриситет экваториального эллипса нейтронной звезды. Частота гравитационных волн, как оказывается, равна удвоенной частоте вращения.
Как видно из этой формулы, зависимость мощности гравитационного излучения от угловой скорости
 значительно более сильная, чем в случае магнитно-дипольного излучения. Поэтому заметный эффект может быть только у очень быстро вращающихся пульсаров, например, у NP 0531 (см. об этом в § 24). В том случае, когда центр магнитного диполя не совпадает с центром нейтронной звезды, излучение будет асимметричным. В этом случае звезда приобретет импульс отдачи в направлении от вращения. Не этим ли объясняются высокие скорости пульсаров?
значительно более сильная, чем в случае магнитно-дипольного излучения. Поэтому заметный эффект может быть только у очень быстро вращающихся пульсаров, например, у NP 0531 (см. об этом в § 24). В том случае, когда центр магнитного диполя не совпадает с центром нейтронной звезды, излучение будет асимметричным. В этом случае звезда приобретет импульс отдачи в направлении от вращения. Не этим ли объясняются высокие скорости пульсаров?
Если бы торможение вращающихся нейтронных звезд было обусловлено их магнитно-дипольным излучением, то, как можно показать,


 3. Между тем статистический анализ большого количества пульсаров с известными
3. Между тем статистический анализ большого количества пульсаров с известными
 и
и
 дает эмпирическую зависимость
дает эмпирическую зависимость


 3,4. У пульсара NP 0531, для которого
3,4. У пульсара NP 0531, для которого
 и
и
 наблюдались особенно тщательно, эмпирическая зависимость имеет вид
наблюдались особенно тщательно, эмпирическая зависимость имеет вид


 2,7. Это означает, что рассмотренная выше простая модель торможения намагниченных вращающихся нейтронных звезд недостаточна. И прежде всего предположение, что нейтронная звезда находится в вакууме, заведомо не выполняется. Тем самым задача становится значительно более сложной.
2,7. Это означает, что рассмотренная выше простая модель торможения намагниченных вращающихся нейтронных звезд недостаточна. И прежде всего предположение, что нейтронная звезда находится в вакууме, заведомо не выполняется. Тем самым задача становится значительно более сложной.
Вращающийся намагниченный проводник создает в окружающем пространстве электрическое поле. Составляющая этого поля, перпендикулярная к поверхности проводника, будет стремиться «вырвать» из него электроны и ионы. В реальных условиях нейтронной звезды напряженность электрического поля достигает огромных значений. К тому же температура поверхности нейтронной звезды достаточно высока. По этим причинам пространство вокруг нейтронной звезды заполнится большим количеством заряженных частиц, которые, двигаясь по силовым линиям магнитного поля, будут вместе с нейтронной звездой с той же угловой скоростью вращаться вокруг ее оси. Такое «твердотельное» вращение должно иметь место вплоть до некоторого критического расстояния от оси вращения, т. е. внутри цилиндра. Радиус этого цилиндра R1 = c/
 определяется условием, что на его поверхности скорость твердотельного вращения равна скорости света[ 54 ]. Однако если плотность плазмы вокруг нейтронной звезды достаточно велика, область ее твердотельного вращения будет меньше и определится условием равенства плотностей магнитной энергии и кинетической энергии плазмы.
определяется условием, что на его поверхности скорость твердотельного вращения равна скорости света[ 54 ]. Однако если плотность плазмы вокруг нейтронной звезды достаточно велика, область ее твердотельного вращения будет меньше и определится условием равенства плотностей магнитной энергии и кинетической энергии плазмы.
Итак, вращающаяся намагниченная нейтронная звезда окружает себя довольно плотной магнитосферой, в электродинамическом смысле являющейся ее продолжением. Как показывают расчеты, электрические заряды в магнитосфере нейтронной звезды должны быть разделены, т. е. там должны быть значительные объемные заряды. Плотность зарядов определяется формулой
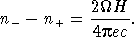 (22.4)
(22.4)
Например, на поверхности пульсара NP 0531, где H
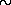 3
3
 1012 Э, a
1012 Э, a
 = 200 с-1, n-- n+
= 200 с-1, n-- n+
 1013 см-3, т. е. довольно значительная. Конечно, полная плотность плазмы около поверхности этого пульсара должна быть гораздо больше.
1013 см-3, т. е. довольно значительная. Конечно, полная плотность плазмы около поверхности этого пульсара должна быть гораздо больше.
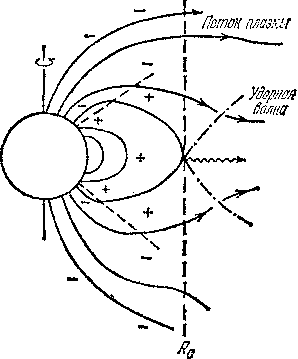 Рис. 22.3: Схема строения магнитосферы пульсара. Rc — радиус светового цилиндра.
Рис. 22.3: Схема строения магнитосферы пульсара. Rc — радиус светового цилиндра.
Заряженные частицы, предварительно ускорившись электрическим полем до релятивистских энергий, будут «вытекать» из магнитосферы на бесконечность по «открытым» силовым линиям, причем заряды разных знаков будут вытекать по разным линиям. На рис. 22.3 приведена схема магнитосферы пульсара для простейшего случая, когда магнитная ось совпадает с осью вращения. В случае, когда оси не совпадают, качественно структура магнитосферы остается такой же.
Около светового цилиндра, который пересекают уходящие в бесконечность магнитные силовые линии, последние уже сильно деформированы потоками вытекающей из магнитосферы пульсара релятивистской плазмы. Поток энергии частиц и магнитного поля, вытекающей через световой цилиндр, можно приближенно оценить формулой
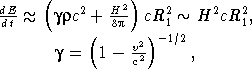 (22.5)
(22.5)
где
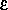 p =
p =
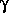
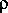 c2 — плотность энергии релятивистских частиц. Если магнитное поле дипольно, то H = H0R3/R13; следовательно,
c2 — плотность энергии релятивистских частиц. Если магнитное поле дипольно, то H = H0R3/R13; следовательно,
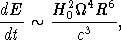 (22.6)
(22.6)
т. е. получается формула, сходная с формулой для мощности магнитно-дипольного излучения в вакууме (22.2). Но, конечно, физическое содержание ее другое: основная часть энергии покидает магнитосферу пульсара в форме потока релятивистских частиц.
Теория позволяет найти только поток энергии этих частиц. Без дополнительных предположений нельзя оценить количество вытекающих из магнитосферы пульсара частиц и среднюю энергию каждой частицы, не говоря уже об энергетическом спектре этих частиц. Рассмотрим конкретно ситуацию в случае пульсара NP 0531. Формула (22.4) в сочетании с законом изменения (n-- n+) как R-3 позволяет определить нижнюю границу потока заряженных частиц через поверхность светового цилиндра этого пульсара:
 (22.7)
(22.7)
С другой стороны, несомненно, что источником энергии излучения всей Крабовидной туманности, мощность которого
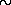 1038 эрг/с, является корпускулярное излучение пульсара NP 0531. Далее, примем во внимание, что энергия релятивистских электронов, находящихся в туманности, лежит в пределах 1010—1014 эВ. Отсюда следует, что поток заряженных частиц через световой цилиндр будет 1036—1040, а концентрация их там
1038 эрг/с, является корпускулярное излучение пульсара NP 0531. Далее, примем во внимание, что энергия релятивистских электронов, находящихся в туманности, лежит в пределах 1010—1014 эВ. Отсюда следует, что поток заряженных частиц через световой цилиндр будет 1036—1040, а концентрация их там
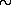 109—1013 см-3, т. е. довольно значительная величина.
109—1013 см-3, т. е. довольно значительная величина.
Таким образом, логическим следствием электродинамики намагниченных вращающихся нейтронных звезд является неизбежность образования вокруг них мощной протяженной магнитосферы со значительным разделением зарядов. Столь же неизбежен вывод о необходимости «пульсарного ветра», т.е. потоков заряженных частиц, вытекающих из магнитосферы по уходящим в бесконечность силовым линиям. Заметим, что этот вывод отнюдь не является тривиальным. До открытия пульсаров молчаливо предполагалось, что атмосферы нейтронных звезд должны иметь совершенно ничтожную протяженность. Например, даже при температуре такой атмосферы
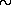 106 К высота однородной водородной атмосферы, вычисленная по известной барометрической формуле h = kT/mHg = kTR2/mHGM, равна
106 К высота однородной водородной атмосферы, вычисленная по известной барометрической формуле h = kT/mHg = kTR2/mHGM, равна
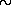 1 см (g = GM/R2 — ускорение силы тяжести на поверхности нейтронной звезды). Столь малое значение h означало бы, что плотность атмосферы нейтронной звезды падала бы практически до нуля на расстоянии в несколько десятков сантиметров. В то же время огромный гравитационный потенциал нейтронных звезд является причиной образования вокруг них очень глубокой «потенциальной ямы», куда должен стекаться межзвездный газ. При некоторых упрощающих предположениях из формулы, описывающей распределение плотности в окрестностях нейтронной звезды, следует, что при r = R = 106 см и T
1 см (g = GM/R2 — ускорение силы тяжести на поверхности нейтронной звезды). Столь малое значение h означало бы, что плотность атмосферы нейтронной звезды падала бы практически до нуля на расстоянии в несколько десятков сантиметров. В то же время огромный гравитационный потенциал нейтронных звезд является причиной образования вокруг них очень глубокой «потенциальной ямы», куда должен стекаться межзвездный газ. При некоторых упрощающих предположениях из формулы, описывающей распределение плотности в окрестностях нейтронной звезды, следует, что при r = R = 106 см и T
 104n
104n
 104n
104n
 , наличие «пульсарного ветра» существенно меняет эту картину. В частности, в такой магнитосфере могут происходить процессы, сопровождаемые неравновесным радиоизлучением огромной мощности.
, наличие «пульсарного ветра» существенно меняет эту картину. В частности, в такой магнитосфере могут происходить процессы, сопровождаемые неравновесным радиоизлучением огромной мощности.
Перейдем теперь к анализу самых общих характеристик этого радиоизлучения. Речь пойдет о природе «окна» излучения, синтетического профиля импульсов, а также о тех характерных вариациях поляризации излучения, которые были описаны в § 21. Что касается природы «окна», то она в основном объясняется «эффектом маяка» (см. рис. 20.1). Это сравнение очень точно. Пучок излучения от некоторого яркого «пятна», жестко связанного с вращающейся нейтронной звездой, описывает в пространстве гигантский конус. Когда пучок проходит через наблюдателя, последний фиксирует импульс радиоизлучения. Геометрической характеристикой пучка является его диаграмма направленности. В предельных случаях последняя может быть «карандашной» или «веерной» (рис. 22.4). В первом случае угловые размеры пучка по всем направлениям приблизительно одинаковы. Во втором случае угловые размеры пучка по одной координате сравнительно невелики, между тем как по другой координате, перпендикулярной к первой, они могут быть равны 360°. С точки зрения механизмов излучения, могут реализовываться как «карандашные», так и «веерные» диаграммы.
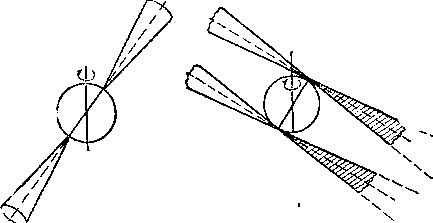 Рис. 22.4: Схема «карандашной» (слева) и «веерной» диаграмм направленности излучения.
Рис. 22.4: Схема «карандашной» (слева) и «веерной» диаграмм направленности излучения.
Из наблюдения профиля импульсов следует, что ширина «окна» около 9° (см. § 21). Однако, как правило, эти профили имеют довольно богатую структуру, в частности, они состоят из значительно более узких субимпульсов. Возникает вопрос: чем объясняются эти субимпульсы? В принципе имеются две возможности объяснения этого эффекта: а) излучение исходит из одной очень маленькой области, жестко связанной с вращающейся нейтронной звездой. В этом случае субимпульсы следует объяснить сложным, как бы «изрезанным» характером диаграммы излучения; б) излучение каждого субимпульса исходит из определенного «пятна» на вращающейся нейтронной звезде и имеет простую (т. е. не «изрезанную») диаграмму. Наличие нескольких субимпульсов означает, что излучающие «пятна» разбросаны по довольно значительной области вращающейся нейтронной звезды. Тот факт, что субимпульсы имеют тенденцию сохранять свою «индивидуальность» в течение нескольких периодов вращения и, кроме того, имеют определенную поляризацию, говорит в пользу второй возможности. Таким образом, характерным «элементом» радиоизлучения пульсара является субимпульс, диаграмма излучения которого проста, а состояние поляризации определенно. Наблюдаемый профиль пульсара определяется последовательностью таких субимпульсов, проходящих через пульсарное «окно».
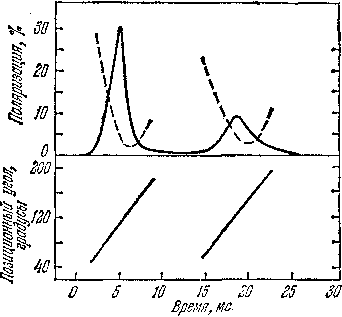 Рис. 22.5: Изменения вектора поляризации оптического излучения пульсара NP0531.
Рис. 22.5: Изменения вектора поляризации оптического излучения пульсара NP0531.
При такой интерпретации относительная длительность импульсов определяется протяженностью области, где находятся излучающие «пятна». Что касается «интеримпульсов», наблюдаемых у некоторых пульсаров, то они объясняются «пятнами», находящимися совсем в другой (почти диаметрально противоположной) области вращающейся нейтронной звезды. Наблюдаемое у пульсара в Крабовидной туманности (а также у некоторых других пульсаров) сравнительно слабое излучение между импульсами следует объяснить распределением излучающих областей по большому объему в окрестностях нейтронной звезды.
Какая же причина «держит» излучающие пятна в строго определенных областях вокруг вращающейся нейтронной звезды? Очевидно, что такой причиной может быть только очень сильное магнитное поле. Естественно также связать наблюдаемую поляризацию и ее изменения по мере прохождения субимпульсов через пульсарное «окно» с изменением ориентации магнитного поля по отношению к наблюдателю из-за вращения нейтронной звезды.
Очень большие и характерные изменения направления вектора поляризации оптического излучения пульсара в Крабовидной туманности (рис. 22.5) и радиоизлучения пульсара PSR 0833—45 (рис. 22.6) проще всего объяснить «карандашной» диаграммой. В обоих этих случаях через пульсарное «окно» проходит, по существу один субимпульс; следовательно, излучение исходит от сравнительно небольших излучающих пятен. Вероятнее всего, что эти «пятна» связаны с магнитными полюсами соответствующих нейтронных звезд. Расчеты, которые мы здесь приводить не будем, показывают, что вращение вектора магнитной оси полностью объясняет наблюдаемые быстрые вариации направления поляризации. Применительно к пульсару в Крабовидной туманности эта теория дает интересную дополнительную информацию. Из скорости изменения направления линейной поляризации оптического излучения этого пульсара следует, что его магнитная ось почти перпендикулярна к оси вращения, причем наименьший угол, образуемый магнитной осью с лучом зрения, равен всего лишь 2°. Любопытно отметить, что радиоизлучение от пульсара в Крабовидной туманности не показывает таких закономерных изменений направления поляризации, как оптическое излучение.
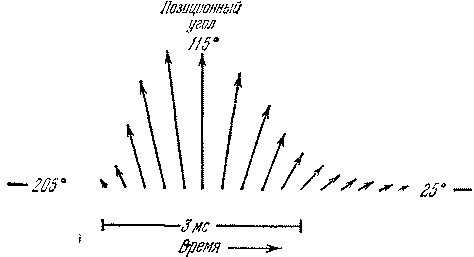 Рис. 22.6: Изменения вектора поляризации радиоизлучения пульсара PSR 0833—45 за время наблюдения одного импульса.
Рис. 22.6: Изменения вектора поляризации радиоизлучения пульсара PSR 0833—45 за время наблюдения одного импульса.
Как же образуются пучки направленного излучения, которые вращаются в пространстве, будучи «привязаны» к вращающейся нейтронной звезде? Как это ни странно, на этот четкий вопрос однозначного ответа пока нет. Разные группы исследователей придерживаются разных мнений.
Так, например, первый астроном, понявший природу пульсаров, Голд, образование пучка излучения связывает с магнитосферой нейтронной звезды, жестко с нею соединенной и вместе с ней вращающейся. Гипотеза Голда ясна из схемы, изображенной на рис. 20.1. Ионизованный газ (плазма) находится в магнитосфере пульсара и вращается вместе с последней с той же угловой скоростью, что и нейтронная звезда. По мере приближения (изнутри) к поверхности «светового цилиндра» скорость вращения приближается к скорости света. При этом в силу эффекта специальной теории относительности, вращающиеся вокруг оси нейтронной звезды электроны плазмы будут излучать частоты, близкие к частоте
 (E/mc2)2, где E =
(E/mc2)2, где E =
 mc2 = mc2
mc2 = mc2
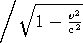 — энергия электронов, вращающихся со скоростью 3, достаточно близкой к c. Релятивистские заряженные частицы всегда излучают внутри некоторого конуса, ось которого совпадает с вектором их мгновенной скорости, а угловой «раскрыв»
— энергия электронов, вращающихся со скоростью 3, достаточно близкой к c. Релятивистские заряженные частицы всегда излучают внутри некоторого конуса, ось которого совпадает с вектором их мгновенной скорости, а угловой «раскрыв»
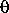 = mc2/E. Всегда можно представить, что около поверхности светового цилиндра плазма распределена не равномерно, а концентрируется в отдельных облаках. Последнее обстоятельство и объясняет наличие пучков излучения.
= mc2/E. Всегда можно представить, что около поверхности светового цилиндра плазма распределена не равномерно, а концентрируется в отдельных облаках. Последнее обстоятельство и объясняет наличие пучков излучения.
В какой-то мере сходную «кинематическую» картину радиоизлучения пульсаров развивали и другие авторы, особенно В. В. Железняков и Г. Смит. Согласно этой картине в магнитосфере пульсара вблизи светового цилиндра имеется область, заполненная плазмой, являющейся источником неравновесного, почти изотропного радиоизлучения. При твердотельном вращении магнитосферы вместе с находящимся в ней облаком из-за эффекта Доплера будет резко увеличиваться частота излучения, когда последнее направлено к наблюдателю. При этом очень сильно будет меняться интенсивность излучения. Таким образом, с точки зрения внешнего наблюдателя такое излучение будет остронаправленным.
Несомненным достоинством «кинематических» теорий радиоизлучения пульсара является возможность непринужденного объяснения одинаковости диаграммы излучения для разных частот. Особенно это относится к пульсару в Крабовидной туманности, импульсы рентгеновского излучения которого практически одновременны с импульсами радиоизлучения. Однако объяснить поляризацию излучения пульсаров и характерные изменения ее со временем очень трудно в рамках только одного «кинематического» механизма.
Совершенно другую геометрию излучения предложили Радхакришнан и Кук. В развитой ими картине излучение вовсе не обязательно связывать с поверхностью светового цилиндра. Излучающим агентом также являются релятивистские электроны, но они релятивистские «сами по себе», а не потому, что движутся (вращаются) с почти световой скоростью, находясь около поверхности светового цилиндра (как в модели Голда). Релятивистские электроны в картине Радхакришнана — Кука движутся в области магнитных полюсов нейтронной звезды и излучают благодаря некоторой модификации синхротронного механизма. В отличие от обычного синхротронного механизма, где релятивистские электроны движутся по спирали вокруг магнитных силовых линий, причем угол между векторами скорости и поля достаточно велик, здесь электроны движутся практически точно по силовым линиям, а излучают только благодаря кривизне последних. В этом смысле рассмотренный выше механизм Голда также, конечно, является синхротронным.
Хотя применение «обобщенного» (так называемого изгибного) синхротронного механизма к радиоизлучению пульсаров представляет несомненный интерес, так как довольно непринужденно объясняет важнейшее его свойство, а именно — направленность, при более детальном рассмотрении обнаруживаются серьезные трудности. Дело в том, что ширина пучков, определяющая длительность субимпульсов, должна хотя и слабо, но все же зависеть от частоты излучения. Ничего подобного, однако, не наблюдается. На всех частотах длительность субимпульсов одинакова. Имеются также серьезные расхождения между наблюдаемыми свойствами поляризации пульсарного радиоизлучения и ожидаемыми согласно той или иной модификации синхротронного механизма.
Резюмируя, следует сказать, что общепринятой теории радиоизлучения пульсаров пока еще нет, хотя отдельные ее элементы, по-видимому, имеются. Вся сложная картина радиоизлучения пульсаров должна определяться совокупным влиянием большого числа факторов: сильного магнитного поля, коллективным взаимодействием заряженных частиц и полей и, конечно, движением плазмы с релятивистской скоростью около внутренней границы светового цилиндра.
До сих пор мы в основном обсуждали вопрос о «геометрии» излучения. Теперь следует остановиться на тех физических процессах, которые могут быть его причиной. Прежде всего рассмотрим вопрос о мощности излучения пульсаров. Последнюю можно найти, измеряя поток излучения во всем радиодиапазоне в течение импульса, зная отношение длительности импульса и период у пульсара и задаваясь видом диаграммы излучения (карандашная, веерная). Полученная таким образом мощность для разных импульсов меняется в очень широких пределах — от 1027 до 1031 эрг/с или, соответственно, от 1014 до 1018 МВт. Эту мощность любопытно сравнить с совокупной мощностью всех земных радио- и телепередатчиков, работающих в том же диапазоне частот, которые при условии, что они работают одновременно, излучали бы несколько тысяч мегаватт. Как видим, естественные космические радиопередатчики неизмеримо мощнее искусственных земных.
Особняком стоит пульсар в Крабовидной туманности. Наряду с радиоизлучением, средняя мощность которого
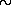 1031 эрг/с (на короткое время она иногда увеличивается в сотню раз), этот пульсар излучает также в оптическом, рентгеновском и гамма-диапазонах. Мощность его оптического излучения, которое отличается удивительной стабильностью, достигает
1031 эрг/с (на короткое время она иногда увеличивается в сотню раз), этот пульсар излучает также в оптическом, рентгеновском и гамма-диапазонах. Мощность его оптического излучения, которое отличается удивительной стабильностью, достигает
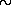 1034 эрг/с, что в 2,5 раза превосходит мощность излучения Солнца. Но основная мощность излучается этим пульсаром в рентгеновском и гамма-диапазонах. Излучаемая мощность в «жестких» квантах этого диапазона достигает значения
1034 эрг/с, что в 2,5 раза превосходит мощность излучения Солнца. Но основная мощность излучается этим пульсаром в рентгеновском и гамма-диапазонах. Излучаемая мощность в «жестких» квантах этого диапазона достигает значения
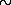 3
3
 1037 эрг/с, что в десять тысяч раз превосходит мощность излучения Солнца на оптических частотах и близка к мощности излучения звезд-гигантов на частотах оптического, инфракрасного и ультрафиолетового диапазонов.
1037 эрг/с, что в десять тысяч раз превосходит мощность излучения Солнца на оптических частотах и близка к мощности излучения звезд-гигантов на частотах оптического, инфракрасного и ультрафиолетового диапазонов.
Представляет интерес оценить для пульсаров мощность излучения единицы объема в излучающей области. Учитывая геометрию пульсаров, можно сделать вывод, что протяженность излучающей области «в глубину» не может превосходить радиуса светового цилиндра. С другой стороны, из длительности импульсов следует, что проекция этой области на поверхность нейтронной звезды должна иметь линейные размеры порядка нескольких десятых ее радиуса. Отсюда, в частности, следует, что у пульсара в Крабовидной туманности объем излучающей области не превосходит 1023 см3. Поэтому излучаемая единицей объема мощность в рентгеновском и гамма-диапазонах у этого пульсара превосходит
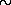 1014 эрг/см3
1014 эрг/см3
 с. Это фантастически большая величина, в миллиарды раз превосходящая мощность генерации термоядерной энергии в единице объема звездных недр.
с. Это фантастически большая величина, в миллиарды раз превосходящая мощность генерации термоядерной энергии в единице объема звездных недр.
Важной характеристикой интенсивности излучения является яркостная температура (см. § 4). Если для оптического излучения пульсара в Крабовидной туманности яркостная температура близка к десяти миллиардам кельвинов, а в рентгеновском диапазоне она равна «всего лишь» сотне тысяч кельвинов, то в радиодиапазоне она достигает огромной величины
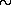 1028 кельвинов!
1028 кельвинов!
Непомерно мощное радиоизлучение пульсара в Крабовидной туманности (а также всех других пульсаров) совершенно исключает возможность его объяснения суммой независимо излучающих заряженных частиц, как это имеет место в случае синхротронного или теплового излучения. С аналогичной ситуацией астрономы встретились еще в сороковых годах, когда радиоастрономические наблюдения обнаружили гигантские всплески солнечного радиоизлучения. Изучение этого интересного явления заставило сделать вывод, что оно возникает при упорядоченных «когерентных» движениях электронов в сравнительно больших объемах плазмы. При таких упорядоченных движениях элементарных зарядов складываются амплитуды излучаемых ими элементарных электромагнитных волн. Следовательно, интенсивность результирующей электромагнитной волны от всей системы излучающих зарядов (пропорциональная квадрату результирующей амплитуды) будет в огромное число раз больше суммы интенсивностей элементарных волн, излучаемых отдельными зарядами. В лабораторных условиях хорошим примером радиоизлучения упорядоченно (когерентно) движущихся электрических зарядов являются обычные передающие антенны. Например, передающая антенна с эффективной поверхностью в десять тысяч квадратных метров может излучать мощность в несколько мегаватт. Если бы вся поверхность, окружающая магнитосферу пульсара в Крабовидной туманности, была покрыта такими передающими антеннами, то мощность излучения была бы всего лишь
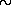 109 МВт, т. е. в десять миллиардов раз меньше мощности радиоизлучения этого пульсара. Даже если бы весь объем его магнитосферы был плотно заполнен такими передающими антеннами, то мощность излучения была бы в сотню тысяч раз меньше наблюдаемой! Этот пример демонстрирует всю ничтожность творения рук и мозга людей по сравнению с естественными процессами в природе.
109 МВт, т. е. в десять миллиардов раз меньше мощности радиоизлучения этого пульсара. Даже если бы весь объем его магнитосферы был плотно заполнен такими передающими антеннами, то мощность излучения была бы в сотню тысяч раз меньше наблюдаемой! Этот пример демонстрирует всю ничтожность творения рук и мозга людей по сравнению с естественными процессами в природе.
Исключительно высокая яркостная температура может быть реализована также и в том случае, когда механизм радиоизлучения представляет собой некоторую разновидность процесса мазерного усиления. В § 4 мы уже познакомились с естественными космическими мазерами, которые так неожиданно оказались связанными с процессом звездообразования. В этом случае мазерное усиление имеет место только для узкого интервала частот, соответствующего радиолиниям молекул OH и H2O. Однако процесс мазерного усиления при некоторых условиях может происходить и в очень широком спектральном интервале, совершенно не связанном с той или иной радиолинией.
Следует еще раз подчеркнуть необычность условий, в которых имеет место генерация и распространение радиоволн. Например, напряженность электрического поля в пульсарном излучении в области генерации доходит до нескольких миллиардов вольт/метр. Отсюда непосредственно следует вывод, что это «собственное» электрическое поле «само по себе» ускоряет «породившие» его электроны до релятивистских энергий. В этой сложной ситуации такие элементарные понятия как показатель преломления, суперпозиция волн и др. уже теряют обычный смысл.
Резюмируя, следует сказать, что радиоизлучение пульсаров представляет собой некоторый когерентный процесс, возникающий в весьма необычных условиях. Для того чтобы такое излучение как-то возникло, необходимо, чтобы в магнитосфере пульсаров было достаточное количество свободных электронов. Необходимость существования свободных электронов в магнитосфере пульсаров следует из основных законов электродинамики (см. выше). Кроме того, имеется довольно мощный поток плазмы, вытекающий с поверхности нейтронной звезды. Это явление мы назвали «пульсарным ветром». Концентрация частиц в таком потоке может быть довольно значительной. Подробнее об этом мы уже говорили применительно к пульсару, находящемуся в Крабовидной туманности. К сожалению, при современном уровне теории неясно, в какой области магнитосферы пульсаров происходит генерация радиоволн. Это может быть слой около магнитных полюсов, непосредственно примыкающий к поверхности нейтронной звезды, или же далекая периферия магнитосферы около внутренней поверхности светового цилиндра. Предстоит еще очень большая работа как наблюдателей, так и теоретиков, чтобы природа радиоизлучения пульсаров, связанная с «активностью» нейтронных звезд, была понята.
Важной особенностью плазмы магнитосферы пульсаров является то, что она состоит не из электронов и положительных ионов (как обычная плазма), а из электронов и позитронов. Само образование такой плазмы можно себе представить следующим образом. Вблизи твердой поверхности сильно намагниченной быстровращающейся нейтронной звезды возникает электрическое поле с составляющей вдоль магнитного поля, отличной от нуля. Это поле вырывает из поверхностных слоев нейтронной звезды первичные заряженные частицы и ускоряет их до огромных значений энергии
 107—108mc2. Двигаясь вдоль искривленных магнитных силовых линий, эти частицы генерируют кванты гамма-излучения. В сильном магнитном поле нейтронной звезды каждый такой квант распадается на электрон и позитрон, которые, в свою очередь, порождают гамма-кванты «изгибного» излучения. Таким образом, в магнитосфере пульсара непрерывно образуются электронно-позитронные лавины, «питающие» находящуюся там плазму. Потоки этой специфической плазмы все время движутся с релятивистскими скоростями от поверхности нейтронной звезды наружу. Когерентно излучающие сгустки такой плазмы и являются «материальным носителем» радиоизлучения пульсаров.
107—108mc2. Двигаясь вдоль искривленных магнитных силовых линий, эти частицы генерируют кванты гамма-излучения. В сильном магнитном поле нейтронной звезды каждый такой квант распадается на электрон и позитрон, которые, в свою очередь, порождают гамма-кванты «изгибного» излучения. Таким образом, в магнитосфере пульсара непрерывно образуются электронно-позитронные лавины, «питающие» находящуюся там плазму. Потоки этой специфической плазмы все время движутся с релятивистскими скоростями от поверхности нейтронной звезды наружу. Когерентно излучающие сгустки такой плазмы и являются «материальным носителем» радиоизлучения пульсаров.
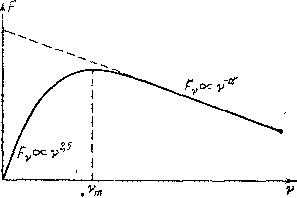 Рис. 22.7: Спектр источника с синхротронной реабсорбцией.
Рис. 22.7: Спектр источника с синхротронной реабсорбцией.
Несомненно, что природа высокочастотного излучения пульсара NP 0531, находящегося в Крабовидной туманности, радикально отличается от природы его радиоизлучения. Это ясно видно хотя бы из общего спектра электромагнитного излучения этого пульсара, приведенного на рис. 20.6. Радио- и высокочастотный спектры никак не «сшиваются», т. е. высокочастотное излучение (в котором, кстати сказать, заключена подавляюще большая часть энергии) никоим образом не является «продолжением» радиоизлучения этого пульсара. Кроме того, между ними имеется еще одно фундаментальное различие: высокочастотное излучение весьма постоянно, т. е. профиль импульсов не меняется со временем, радиоизлучение же переменно и по-другому поляризовано. Все факты говорят о том, что в то время как радиоизлучение NP 0531, так же, как и радиоизлучение других пульсаров, обусловлено неким, пока неизвестным «когерентным» механизмом, высокочастотное излучение есть сумма излучений отдельных релятивистских электронов, движущихся в магнитосфере пульсара, т. е. является синхротронным. Эго значительно упрощает задачу теоретического истолкования наблюдаемых свойств оптического и рентгеновского излучения NP 0531.
В основу теории высокочастотного излучения пульсара в Крабовидной туманности, по нашему мнению, следует положить знаменательный факт «завала» его спектра в ближней инфракрасной области. Какова причина этого явления? Автор настоящей книги еще в 1970 г. привел аргументы в пользу того, что этот «завал» следует объяснить явлением «синхротронной реабсорбции», в то время как само высокочастотное излучение пульсара NP 0531 объясняется обычным «синхротронным» механизмом, являющимся причиной основной части излучения Крабовидной туманности во всем диапазоне электромагнитных волн (см. § 17). Само явление синхротронной реабсорбции состоит в том, что при очень большой плотности релятивистских частиц космический объект перестает быть прозрачным для «собственного» синхротронного излучения. Эта непрозрачность начинается на некоторой частоте и прогрессивно растет в сторону низких частот. По этой причине интенсивность на низких частотах как бы «срезается» и синхротронный спектр источника приобретает вид, изображенный на рис. 22.7. На этом же рисунке для сравнения прерывистой линией изображен спектр того же источника при условии его прозрачности, т. е. при отсутствии синхротронной реабсорбции. Мы видим, что характер высокочастотного спектра пульсара в Крабовидной туманности (см. рис. 20.6) такой же, как у источника, где существенна синхротронная реабсорбция.
Значение частоты
 m, начиная с которой эффект синхротронной реабсорбции становится существенным, тем выше, чем «компактнее» источник, т. е. прежде всего чем больше плотность находящихся там релятивистских электронов.
m, начиная с которой эффект синхротронной реабсорбции становится существенным, тем выше, чем «компактнее» источник, т. е. прежде всего чем больше плотность находящихся там релятивистских электронов.
Угловые размеры источника синхротронного излучения, в спектре которого наблюдается синхротронная реабсорбция, определяются формулой
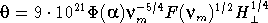 (22.8)
(22.8)
где
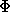 (
(
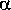 ) — безразмерный множитель порядка единицы,
) — безразмерный множитель порядка единицы,
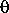 выражается в секундах дуги. Эта очень важная для радиоастрономии формула впервые была получена в 1963 г. советским радиоастрономом В. И. Слышем. Тогда она была особенно полезной для изучения природы только что открытых квазаров, радиоспектры которых часто показывают явление синхротронной реабсорбции на частотах, лежащих в диапазоне сотен и тысяч мегагерц (что соответствует дециметровым и сантиметровым волнам). Тот факт, что в случае пульсара в Крабовидной туманности
выражается в секундах дуги. Эта очень важная для радиоастрономии формула впервые была получена в 1963 г. советским радиоастрономом В. И. Слышем. Тогда она была особенно полезной для изучения природы только что открытых квазаров, радиоспектры которых часто показывают явление синхротронной реабсорбции на частотах, лежащих в диапазоне сотен и тысяч мегагерц (что соответствует дециметровым и сантиметровым волнам). Тот факт, что в случае пульсара в Крабовидной туманности
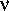 m
m
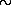 1014 с-1 (сто миллионов мегагерц), сам по себе весьма поразителен. Он означает, прежде всего, что этот пульсар представляет собой «сверхкомпактный» источник.
1014 с-1 (сто миллионов мегагерц), сам по себе весьма поразителен. Он означает, прежде всего, что этот пульсар представляет собой «сверхкомпактный» источник.
Анализ показывает, что в области синхротронного оптического и рентгеновского излучения пульсара в Крабовидной туманности H

 3
3
 103 Э, в то время как полное значение вектора напряженности магнитного поля там
103 Э, в то время как полное значение вектора напряженности магнитного поля там
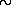 106 Э. Это означает, что излучающая область находится где-то вблизи светового цилиндра, радиус которого для пульсара NP 0531 равен
106 Э. Это означает, что излучающая область находится где-то вблизи светового цилиндра, радиус которого для пульсара NP 0531 равен
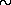 1,5 тысяч километров, что в 100—200 раз больше радиуса нейтронной звезды. По этой причине напряженность магнитного поля в области светового цилиндра в несколько миллионов раз меньше, чем на поверхности нейтронной звезды.
1,5 тысяч километров, что в 100—200 раз больше радиуса нейтронной звезды. По этой причине напряженность магнитного поля в области светового цилиндра в несколько миллионов раз меньше, чем на поверхности нейтронной звезды.
На основе теории синхротронного излучения можно вычислить концентрацию релятивистских электронов в магнитосфере пульсара NP 0531 и их поток в Крабовидную туманность. Оказывается, что этот поток как раз достаточен для непрерывного «питания» этой туманности энергией, необходимой для компенсации ее мощного излучения. Таким образом, синхротронная теория естественно объясняет оптическое и рентгеновское излучение едва ли не самого любопытного космического объекта. Что касается происхождения сверхжесткого гамма-излучения (см. сноску на стр. 616), то скорее всего оно обусловлено столкновениями между заряженными частицами, ускоренными до ультравысоких энергий электрическими полями в магнитосфере пульсара NP 0531.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
1. Трудность согласования квантовой теории и теории излучения
1. Трудность согласования квантовой теории и теории излучения Электромагнитная теория, дополненная теорией электронов Лоренца, дает совершенно ясную и точную картину излучения, испускаемого системой движущихся зарядов. Если заданы структура и закон движения системы
Глава 19 Нейтронные звезды и открытие пульсаров
Глава 19 Нейтронные звезды и открытие пульсаров Как уже говорилось во второй части этой книги, заключительная фаза эволюции звезды, наступающая после того, как будут в значительной степени исчерпаны ресурсы ее ядерного водородного горючего, существенно зависит от массы
ЭФФЕКТИВНЫЕ ТЕОРИИ
ЭФФЕКТИВНЫЕ ТЕОРИИ Параметр среднего роста человека находится примерно на середине шкалы (если строить ее в степенях числа десять, т. е. в логарифмическом масштабе) между мельчайшим вообразимым размером и громадностью Вселенной[8]. Мы очень велики по сравнению с
Глава 12 Перспективы развития теории гравитации
Глава 12 Перспективы развития теории гравитации То, что мы называем прогрессом, – является заменой одной неприятности на другую. Генри Хейвлок Эллис Теории гравитации альтернативные ОТО Ничто не делает нашу жизнь столь приятной, как ее неизбежная
Биметрические теории и теории с массивным гравитоном
Биметрические теории и теории с массивным гравитоном Вспомним, чтобы описать слабые гравитационные волны, мы разбивали динамическую метрику ОТО на метрику плоского пространства-времени и возмущения метрики. Оказалось, что возмущения в виде волн могут распространяться
Чутьё на теории
Чутьё на теории Среди всех качеств Якова Борисовича как физика-теоретика, было, с моей точки зрения, особенно замечательное, выделяющее его из среды других теоретиков, — это чутьё на теории. Я имею в виду удивительный дар почувствовать глубину и перспективу теоретической
Теории великого объединения (ТВО) и теории всего сущего (TBC)
Теории великого объединения (ТВО) и теории всего сущего (TBC) Названия лишь вводят в заблуждение, поскольку предлагают больше, чем могут дать. В действительности они лишь указывают на объединение известных взаимодействий в рамках одной, всеобъемлющей теории. ТВО
Шестая глава ДНК теории струн
Шестая глава ДНК теории струн При поиске алмазов, если вам повезет, вы также можете найти и другие драгоценные камни. Когда я заявил о своем доказательстве гипотезы Калаби в 1977 году в своей двухстраничной статье, за которой последовало само доказательство на семидесяти
Глава V. Рассказы о теории и эксперименте
Глава V. Рассказы о теории и эксперименте Когда мы стареем, Мир нам кажется странным. Все сложнее Понять смерть и жизнь. Ведь жизнь Не вспышка без до и после, А пожар без конца и начала. Т. Элиот. Ист Кокер Я хочу теперь рассказать три истории об успехах физики ХХ в. Из всех
Глава VI. Красивые теории
Глава VI. Красивые теории Спеша за облачком или цветком, Душа приют недолгий обретает, Пред ней в сиянии неба голубом Тень вечности, мелькая, исчезает. Генри Воон. Приют В 1974 г. Поль Дирак приехал в Гарвард, чтобы рассказать о своей исторической работе, ставшей одной из
Глава IX. Контуры окончательной теории
Глава IX. Контуры окончательной теории …Если Вы можете глядеть в посев времен И знаете судьбу зерна любого, Скажите мне… В. Шекспир. Макбет33). Акт I, сцена 3 Вполне возможно, что нас отделяют века от окончательной теории, и она окажется совершенно непохожей на то, что мы
ГЛАВА 1 ВОЛНОВАЯ И КОРПУСКУЛЯРНАЯ ТЕОРИИ СВЕТА
ГЛАВА 1 ВОЛНОВАЯ И КОРПУСКУЛЯРНАЯ ТЕОРИИ СВЕТА Людьми, которые сыграли центральную роль в истории теории света, были Гук, Гюйгенс и Ньютон. Гук и Ньютон были британцами, Гюйгенс — голландцем. Все они сделали замечательные вклады в различные области физики и установили
Как возникают теории
Как возникают теории Почти анекдотическая история связана с именем академика Роберта Симмера. В 1759 году английский естествоиспытатель Р. Симмер сделал заключение о том, что в обычном состоянии любое тело содержит равное количество разноименных зарядов, взаимно