Глава 6 Звезда — газовый шар, находящийся в состоянии равновесия
Глава 6 Звезда — газовый шар, находящийся в состоянии равновесия
Представляется почти очевидным тот факт, что подавляющее большинство звезд не меняет своих свойств в течение огромных промежутков времени. Это утверждение совершенно очевидно для интервала времени по крайней мере в 60 лет, в течение которых астрономы разных стран выполнили очень большую работу, по измерению блеска, цвета и спектра множества звезд. Заметим что хотя некоторые звезды меняют свои характеристики (такие звезды называются переменными; см. § 1), изменения носят либо строго периодический либо более или менее периодический характер. Систематические изменения блеска, спектра или цвета у звезд наблюдаются в очень редких случаях. Например, изменения периодов пульсирующих звезд-цефеид хотя и обнаружены, но они настолько малы, что требуется по крайней мере несколько миллионов лет для того, чтобы изменения периода пульсаций стали значительными. С другой стороны, мы знаем (см. § 1), что светимость цефеид меняется с изменением периода. Можно, следовательно, сделать вывод, что в течение по крайней мере нескольких миллионов лет у таких звезд их важнейшая характеристика — мощность излучаемой энергии — меняется мало. На этом примере мы видим, что хотя длительность наблюдений составляет всего лишь несколько десятков лет (срок совершенно ничтожный по космическим масштабам!), можно сделать вывод о постоянстве свойств цефеид в течение неизмеримо больших интервалов времени.
Но в нашем распоряжении есть еще одна возможность оценить время, в течение которого мощность излучения звезд почти не меняется. Из геологических данных следует, что на протяжении по крайней мере последних двух-трех миллиардов лет температура Земли если и менялась, то не больше, чем на несколько десятков градусов. Это следует из непрерывности эволюции жизни на Земле. А если так, то Солнце за этот огромный промежуток времени никогда не излучало ни в три раза сильнее, ни в три раза слабее, чем сейчас. Похоже на то, что в столь длительной истории нашего светила были периоды, когда его излучение значительно (но не очень сильно) отличалось от нынешнего уровня, но такие эпохи были сравнительно кратковременными. Мы имеем в виду ледниковые периоды, о которых речь будет идти в § 9. Но в среднем мощность излучения Солнца за последние несколько миллиардов лет отличалась удивительным постоянством.
В то же время Солнце — довольно типичная звезда. Как мы знаем (см. § 1), оно представляет собой желтый карлик спектрального класса G2. Таких звезд в нашей Галактике насчитывается по крайней мере несколько миллиардов. Вполне логично также сделать вывод, что и большинство других звезд главной последовательности, у которых спектральные классы отличны от солнечного, также должны быть весьма «долгоживущими» объектами.
Итак, подавляющее большинство звезд очень мало меняется со временем. Это, конечно, не означает, что они в «неизменном виде» могут существовать сколь угодно долго. Наоборот, ниже мы покажем, что возраст звезд хотя и очень велик, но конечен. Более того, этот возраст весьма различен для разных звезд и определяется в первую очередь их массой. Но даже самые «короткоживущие» звезды все-таки почти не меняют своих характеристик в течение миллиона лет. Какие же выводы отсюда следуют?
Уже из простейшего анализа спектров звезд вытекает, что их наружные слои должны находиться в газообразном состоянии. В противном случае, очевидно, в этих спектрах никогда не наблюдались бы резкие линии поглощения, характерные для вещества, находящегося в газообразном состоянии. Дальнейший анализ звездных спектров позволяет существенно уточнить свойства вещества наружных слоев звезд (т. е. «звездных атмосфер»), откуда к нам приходит их излучение.
Изучение спектров звезд позволяет с полной достоверностью сделать вывод, что звездные атмосферы представляют собой нагретый до температуры в тысячи и десятки тысяч градусов ионизованный газ, т. е. плазму. Спектральный анализ позволяет определить химический состав звездных атмосфер, который в большинстве случаев примерно такой же, как и у Солнца. Наконец, изучая звездные спектры, можно определить и плотность звездных атмосфер, которая для различных звезд меняется в очень широких пределах. Итак, наружные слои звезд — это газ.
Но в этих слоях заключена ничтожно малая доля массы всей звезды. Хотя непосредственно оптическими методами недра звезд из-за их огромной непрозрачности наблюдать нельзя, мы можем сейчас со всей определенностью утверждать, что и внутренние слои звезд также находятся в газообразном состоянии. Это утверждение отнюдь не является очевидным. Например, поделив массу Солнца, равную 2
 1033 г, на его объем, равный
1033 г, на его объем, равный
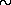 1,4
1,4
 1033 см3, легко найти среднюю плотность (или удельный вес) солнечного вещества, которая будет около 1,4 г/см3, т. е. больше плотности воды. Ясно, что в центральных областях Солнца плотность должна быть значительно выше средней. У большинства карликовых звезд средняя плотность превосходит солнечную. Естественно возникает вопрос: как согласовать наше утверждение, что недра Солнца и звезд находятся в газообразном состоянии со столь высокими плотностями вещества? Ответ на этот вопрос состоит в том, что температура звездных недр, как мы скоро убедимся, очень высока (значительно выше, чем в поверхностных слоях), что исключает возможность существования там твердой или жидкой фазы вещества.
1033 см3, легко найти среднюю плотность (или удельный вес) солнечного вещества, которая будет около 1,4 г/см3, т. е. больше плотности воды. Ясно, что в центральных областях Солнца плотность должна быть значительно выше средней. У большинства карликовых звезд средняя плотность превосходит солнечную. Естественно возникает вопрос: как согласовать наше утверждение, что недра Солнца и звезд находятся в газообразном состоянии со столь высокими плотностями вещества? Ответ на этот вопрос состоит в том, что температура звездных недр, как мы скоро убедимся, очень высока (значительно выше, чем в поверхностных слоях), что исключает возможность существования там твердой или жидкой фазы вещества.
Итак, звезды — это огромные газовые шары. Весьма существенно, что такой газовый шар «цементируется» силой всемирного тяготения, т. е. гравитацией. На каждый элемент объема звезды действует сила гравитационного притяжения от всех остальных элементов звезды. Именно эта сила препятствует разлету различных частей газа, образующего звезду, в окружающее пространство. Если бы не было этой силы, газ, образующий звезду, вначале расплылся бы, образовав нечто вроде плотной туманности, а потом окончательно рассеялся бы в огромном, окружающем звезду межзвездном пространстве. Сделаем очень грубую оценку, сколько бы потребовалось времени, чтобы при таком «расплывании» размер звезды увеличился бы, скажем, в 10 раз. Примем, что «расплывание» происходит с тепловой скоростью атомов водорода (из которого в основном состоит звезда) при температуре наружных слоев звезды, т. е. около 10 000 К. Эта скорость близка к 10 км/с, т. е. 106 см/с. Так как радиус звезды можно принять близким к миллиону километров (т. е. 1011 см), то для интересующего нас «расплывания» с десятикратным увеличением размеров звезды потребуется ничтожно малое время t = 10
 1011/106 = 106 секунд
1011/106 = 106 секунд
 10 суток!
10 суток!
Это означает, что если бы не сила гравитационного притяжения, звезды рассеялись бы в окружающем пространстве за ничтожно малое (по астрономическим понятиям) время, исчисляемое сутками для звезд-карликов или годами для гигантов. Значит, без силы всемирного тяготения не было бы звезд. Действуя непрерывно, эта сила стремится сблизить между собой различные элементы звезды. Очень важно подчеркнуть, что сила гравитации по самой своей природе стремится неограниченно сблизить между собой все частицы звезды, т. е. в пределе как бы «собрать всю звезду в точку». Но если бы на частицы, образующие звезду, действовала только сила всемирного тяготения, то звезда стала бы катастрофически быстро сжиматься. Оценим сейчас время, в течение которого это сжатие станет существенным. Если бы никакая сила не противодействовала гравитации, вещество звезды падало бы по направлению к ее центру по законам свободного падения тел. Рассмотрим элемент вещества внутри звезды где-нибудь между ее поверхностью и центром на расстоянии R от последнего. На этот элемент действует ускорение силы тяготения g =
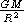 , где G — гравитационная постоянная (см. стр. 15), M — масса, лежащая внутри сферы радиуса R. По мере падения к центру как M, так и R будут меняться, следовательно, будет меняться и g. Мы, однако, не сделаем большой ошибки в нашей оценке, если предположим, что M и R остаются постоянными. Применив к решению нашей задачи элементарную формулу механики, связывающую пройденный при свободном падении путь R с величиной ускорения g, получим уже выведенную в § 3 первой части формулу (3.6)
, где G — гравитационная постоянная (см. стр. 15), M — масса, лежащая внутри сферы радиуса R. По мере падения к центру как M, так и R будут меняться, следовательно, будет меняться и g. Мы, однако, не сделаем большой ошибки в нашей оценке, если предположим, что M и R остаются постоянными. Применив к решению нашей задачи элементарную формулу механики, связывающую пройденный при свободном падении путь R с величиной ускорения g, получим уже выведенную в § 3 первой части формулу (3.6)
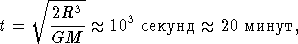
где t — время падения, причем мы положили R
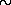 R
R
 , a M
, a M
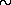 M
M
 . Таким образом, если бы никакая сила не противодействовала гравитации, наружные слои звезды буквально рухнули бы, а звезда катастрофически бы сжалась за какую-нибудь долю часа!
. Таким образом, если бы никакая сила не противодействовала гравитации, наружные слои звезды буквально рухнули бы, а звезда катастрофически бы сжалась за какую-нибудь долю часа!
Какая же сила, непрерывно действующая во всем объеме звезды, противодействует силе гравитации? Заметим, что в каждом элементарном объеме звезды направление этой силы должно быть противоположно, а величина равна силе притяжения. В противном случае происходили бы локальные, местные нарушения равновесия, приводившие за очень короткое время, которое мы только что оценили, к большим изменениям в структуре звезды.
Силой, противодействующей гравитации, является давление газа[ 16 ]. Последнее непрерывно стремится расширить звезду, «рассеять» ее на возможно больший объем. Выше мы уже оценили, как быстро «рассеялась» бы звезда, если бы отдельные ее части не сдерживались силой гравитации. Итак, из того простого факта, что звезды — газовые шары в практически неизменном виде (т. е. не сжимаясь и не расширяясь) существуют по меньшей мере миллионы лет, следует, что каждый элемент вещества звезды находится в равновесии под действием противоположно направленных сил гравитации и газового давления. Такое равновесие называется «гидростатическим». Оно широко распространено в природе. В частности, земная атмосфера находится в гидростатическом равновесии под действием силы гравитационного притяжения Земли и давления находящихся в ней газов. Если бы не было давления, земная атмосфера очень быстро «упала» бы на поверхность нашей планеты. Следует подчеркнуть, что гидростатическое равновесие в звездных атмосферах осуществляется с огромной точностью. Малейшее его нарушение сразу же приводит к появлению сил, меняющих распределение вещества в звезде, после чего происходит такое его перераспределение, при котором равновесие восстанавливается. Здесь мы всегда говорим об обычных «нормальных» звездах. В исключительных случаях, о которых в этой книге будет идти речь, нарушение равновесия между силой гравитации и давлением газа приведет к весьма серьезным, даже катастрофическим последствиям в жизни звезды. А сейчас мы можем только сказать, что история существования любой звезды — это поистине титаническая борьба между силой гравитации, стремящейся ее неограниченно сжать, и силой газового давления, стремящейся ее «распылить», рассеять в окружающем межзвездном пространстве. Многие миллионы и миллиарды лет длится эта «борьба». В течение этих чудовищно больших сроков силы равны. Но в конце концов, как мы увидим дальше, победа будет за гравитацией. Такова драма эволюции любой звезды. Ниже мы будем довольно подробно останавливаться на отдельных этапах этой драмы, связанных с финальными стадиями эволюции звезд.
В центральной части «нормальной» звезды вес вещества, заключенного в столбе, площадь основания которого равна одному квадратному сантиметру, а высота — радиусу звезды, будет равен давлению газа у основания столба. С другой стороны, масса столба равна силе, с которой он притягивается к центру звезды.
Мы сейчас проведем весьма упрощенный расчет, который, тем не менее, вполне отражает существо вопроса. А именно, положим массу нашего столба M1 =
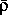 R, где
R, где
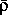 — средняя плотность звезды, и будем считать, что «эффективное» расстояние между центром звезды и основанием столба равно R/2. Тогда условие гидростатического равновесия запишется так:
— средняя плотность звезды, и будем считать, что «эффективное» расстояние между центром звезды и основанием столба равно R/2. Тогда условие гидростатического равновесия запишется так:
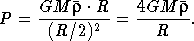 (6.1)
(6.1)
Сделаем теперь оценку величины газового давления P в центральной части такой звезды, какой является наше Солнце. Подставив численное значение величин, стоящих в правой части этого уравнения, найдем, что P = 1016 дин/см2, или 10 миллиардов атмосфер! Это неслыханно большая величина. Самое высокое «стационарное» давление, достигаемое в земных лабораториях, порядка нескольких миллионов атмосфер[ 17 ].
Из элементарного курса физики известно, что давление газа зависит от его плотности
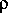 и температуры T. Формула, связывающая все эти величины, носит название «формулы Клапейрона»: P =
и температуры T. Формула, связывающая все эти величины, носит название «формулы Клапейрона»: P =
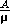
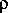 T. С другой стороны, плотность в центральных областях «нормальных» звезд, конечно, больше, чем средняя плотность, но не существенно больше. В таком случае, из формулы Клапейрона непосредственно следует, что одна лишь большая плотность звездных недр сама по себе не в состоянии обеспечить достаточно высокое давление газа, чтобы выполнялось условие гидростатического равновесия. Необходимо прежде всего, чтобы температура газа была достаточно высока.
T. С другой стороны, плотность в центральных областях «нормальных» звезд, конечно, больше, чем средняя плотность, но не существенно больше. В таком случае, из формулы Клапейрона непосредственно следует, что одна лишь большая плотность звездных недр сама по себе не в состоянии обеспечить достаточно высокое давление газа, чтобы выполнялось условие гидростатического равновесия. Необходимо прежде всего, чтобы температура газа была достаточно высока.
В формулу Клапейрона входит также средняя молекулярная масса
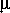 . Основным химическим элементом в атмосферах звезд является водород, и нет оснований полагать, что в недрах по крайней мере большинства звезд химический состав должен существенно отличаться от наблюдаемого в наружных слоях. В то же время, так как ожидаемая температура в центральных областях звезд должна быть достаточно велика, водород там должен быть почти полностью ионизован, т. е. «расщеплен» на протоны и электроны. Так как масса последних пренебрежимо мала по сравнению с протонами, а количество протонов равно количеству электронов, то средняя молекулярная масса этой смеси должна быть близка к 1/2. Тогда из уравнений (6.1) и формулы Клапейрона следует, что температура в центральных областях звезд по порядку величин равна
. Основным химическим элементом в атмосферах звезд является водород, и нет оснований полагать, что в недрах по крайней мере большинства звезд химический состав должен существенно отличаться от наблюдаемого в наружных слоях. В то же время, так как ожидаемая температура в центральных областях звезд должна быть достаточно велика, водород там должен быть почти полностью ионизован, т. е. «расщеплен» на протоны и электроны. Так как масса последних пренебрежимо мала по сравнению с протонами, а количество протонов равно количеству электронов, то средняя молекулярная масса этой смеси должна быть близка к 1/2. Тогда из уравнений (6.1) и формулы Клапейрона следует, что температура в центральных областях звезд по порядку величин равна
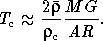 (6.2)
(6.2)
Величина
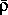 /
/
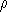 c может быть порядка 1/10. Она зависит от структуры звездных недр (см. § 12). Из формулы (6.2) следует, что температура в центральных областях Солнца должна быть порядка десяти миллионов кельвинов. Более точные расчеты отличаются от полученной нами сейчас оценки всего лишь на 20—30%. Итак, температура в центральных областях звезд исключительно велика — примерно в тысячу раз больше, чем на их поверхности. Теперь обсудим, каковы должны быть свойства вещества, нагретого до такой высокой температуры. Прежде всего такое вещество, несмотря на свою большую плотность, должно находиться в газообразном состоянии. Об этом речь уже шла выше. Но мы можем теперь уточнить это утверждение. При такой высокой температуре свойства газа в недрах звезд, несмотря на его высокую плотность, будут почти неотличимы от свойств идеального газа, т. е. такого газа, в котором взаимодействия между составляющими его частицами (атомами, электронами, ионами) сводятся к столкновениям. Именно для идеального газа справедлив закон Клапейрона, которым мы воспользовались при оценке температуры в центральных областях звезд.
c может быть порядка 1/10. Она зависит от структуры звездных недр (см. § 12). Из формулы (6.2) следует, что температура в центральных областях Солнца должна быть порядка десяти миллионов кельвинов. Более точные расчеты отличаются от полученной нами сейчас оценки всего лишь на 20—30%. Итак, температура в центральных областях звезд исключительно велика — примерно в тысячу раз больше, чем на их поверхности. Теперь обсудим, каковы должны быть свойства вещества, нагретого до такой высокой температуры. Прежде всего такое вещество, несмотря на свою большую плотность, должно находиться в газообразном состоянии. Об этом речь уже шла выше. Но мы можем теперь уточнить это утверждение. При такой высокой температуре свойства газа в недрах звезд, несмотря на его высокую плотность, будут почти неотличимы от свойств идеального газа, т. е. такого газа, в котором взаимодействия между составляющими его частицами (атомами, электронами, ионами) сводятся к столкновениям. Именно для идеального газа справедлив закон Клапейрона, которым мы воспользовались при оценке температуры в центральных областях звезд.
При температуре порядка десяти миллионов кельвинов и при плотностях, которые там существуют, все атомы должны быть ионизованы. В самом деле, средняя кинетическая энергия каждой частицы газа
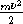 =
=
 kT будет около 10-9 эрг или
kT будет около 10-9 эрг или
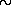 1000 эВ.
1000 эВ.
Это означает, что каждое столкновение электрона с атомом может привести к ионизации последнего, так как энергия связи электронов в атоме (так называемый «потенциал ионизации»), как правило, меньше тысячи электронвольт. Только самые «глубокие» электронные оболочки у тяжелых атомов останутся «нетронутыми», т. е. будут удержаны своими атомами. Состояние ионизации внутри-звездного вещества определяет его среднюю молекулярную массу, величина которой, как мы уже имели возможность убедиться, играет большую роль в недрах звезд. Если бы вещество звезды состояло только из полностью ионизованного водорода (как мы положили выше), то средняя молекулярная масса
 , равнялась бы 1/2. Если бы там был только полностью ионизованный гелий, то
, равнялась бы 1/2. Если бы там был только полностью ионизованный гелий, то
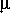 = 4/3 (так как при ионизации одного атома гелия с атомной массой 4 образуются три частицы — ядро гелия плюс два электрона). Наконец, если бы вещество недр звезды состояло только из тяжелых элементов (кислорода, углерода, железа и пр.), то средняя молекулярная масса его при полной ионизации всех атомов была бы близка к 2, так как для таких элементов атомная масса приблизительно вдвое больше, чем число электронов в атоме.
= 4/3 (так как при ионизации одного атома гелия с атомной массой 4 образуются три частицы — ядро гелия плюс два электрона). Наконец, если бы вещество недр звезды состояло только из тяжелых элементов (кислорода, углерода, железа и пр.), то средняя молекулярная масса его при полной ионизации всех атомов была бы близка к 2, так как для таких элементов атомная масса приблизительно вдвое больше, чем число электронов в атоме.
В действительности вещество звездных недр представляет собой некоторую смесь водорода, гелия и тяжелых элементов. Относительное содержание этих основных компонент звездного вещества (не по числу атомов, а по массе) обычно обозначается через буквы X, Y и Z, которые характеризуют химический состав звезды. У типичных звезд, более или менее сходных с Солнцем, X = 0,73, Y = 0,25, Z = 0,02. Отношение Y/X
 0,3 означает, что на каждые 10 атомов водорода приходится приблизительно один атом гелия. Относительное количество тяжелых элементов весьма мало. Например, атомов кислорода примерно в тысячу раз меньше, чем водорода. Тем не менее роль тяжелых элементов в структуре внутренних областей звезд довольно значительна, так как они сильно влияют на непрозрачность звездного вещества. Среднюю молекулярную массу звезды мы можем теперь определить простой формулой:
0,3 означает, что на каждые 10 атомов водорода приходится приблизительно один атом гелия. Относительное количество тяжелых элементов весьма мало. Например, атомов кислорода примерно в тысячу раз меньше, чем водорода. Тем не менее роль тяжелых элементов в структуре внутренних областей звезд довольно значительна, так как они сильно влияют на непрозрачность звездного вещества. Среднюю молекулярную массу звезды мы можем теперь определить простой формулой:
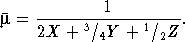 (6.3)
(6.3)
Роль Z в оценке
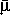 незначительна. Решающее значение для величины средней молекулярной массы имеют X и Y . Для звезд центральной части главной последовательности (в частности, для Солнца)
незначительна. Решающее значение для величины средней молекулярной массы имеют X и Y . Для звезд центральной части главной последовательности (в частности, для Солнца)
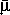 = 0,6. Так как величина
= 0,6. Так как величина
 для большинства звезд меняется в очень незначительных пределах, мы можем написать простую формулу для центральных температур различных звезд, выразив их массы и радиусы в долях солнечной массы M
для большинства звезд меняется в очень незначительных пределах, мы можем написать простую формулу для центральных температур различных звезд, выразив их массы и радиусы в долях солнечной массы M
 и солнечного радиуса R
и солнечного радиуса R
 :
:
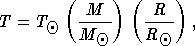 (6.4)
(6.4)
где T
 — температура центральных областей Солнца. Выше, мы грубо оценили T
— температура центральных областей Солнца. Выше, мы грубо оценили T
 в 10 миллионов кельвинов. Точные вычисления дают значение T
в 10 миллионов кельвинов. Точные вычисления дают значение T
 = 14 миллионов кельвинов. Из формулы (6.4) следует, например, что температура недр массивных горячих (на поверхности!) звезд спектрального класса В раза в 2—3 выше температуры солнечных недр, в то время как у красных карликов центральные температуры раза в 2—3 ниже солнечных.
= 14 миллионов кельвинов. Из формулы (6.4) следует, например, что температура недр массивных горячих (на поверхности!) звезд спектрального класса В раза в 2—3 выше температуры солнечных недр, в то время как у красных карликов центральные температуры раза в 2—3 ниже солнечных.
Существенно, что температура
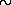 107 К характерна не только для самых центральных областей звезд, но и для окружающего центр звезды большого объема. Учитывая, что плотность звездного вещества растет по направлению к центру, мы можем сделать вывод, что основная часть массы звезды имеет температуру, во всяком случае превышающую
107 К характерна не только для самых центральных областей звезд, но и для окружающего центр звезды большого объема. Учитывая, что плотность звездного вещества растет по направлению к центру, мы можем сделать вывод, что основная часть массы звезды имеет температуру, во всяком случае превышающую
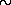 5 миллионов кельвинов. Если мы еще вспомним, что большая часть массы Вселенной заключена в звездах, то напрашивается вывод, что вещество Вселенной, как правило, горячее и плотное. Следует, однако, к этому добавить, что речь идет о современной Вселенной: в далеком прошлом и будущем состояние вещества Вселенной было и будет совсем другим. Об этом речь шла во введении к этой книге.
5 миллионов кельвинов. Если мы еще вспомним, что большая часть массы Вселенной заключена в звездах, то напрашивается вывод, что вещество Вселенной, как правило, горячее и плотное. Следует, однако, к этому добавить, что речь идет о современной Вселенной: в далеком прошлом и будущем состояние вещества Вселенной было и будет совсем другим. Об этом речь шла во введении к этой книге.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
ПОПЫТКИ ПОЛУЧИТЬ БОЛЬШЕ ЭНЕРГИИ ИЗ УГЛЯ — ЭЛЕКТРИЧЕСКИЙ ПРИВОД — ГАЗОВЫЙ ДВИГАТЕЛЬ — ХОЛОДНАЯ УГОЛЬНАЯ БАТАРЕЯ
ПОПЫТКИ ПОЛУЧИТЬ БОЛЬШЕ ЭНЕРГИИ ИЗ УГЛЯ — ЭЛЕКТРИЧЕСКИЙ ПРИВОД — ГАЗОВЫЙ ДВИГАТЕЛЬ — ХОЛОДНАЯ УГОЛЬНАЯ БАТАРЕЯ Я помню, что одно время считал производство электричества за счет сжигания угля в батарее величайшим достижением на пользу развития цивилизации, и я был
ФИГУРЫ РАВНОВЕСИЯ ВРАЩАЮЩЕЙСЯ ЖИДКОСТИ
ФИГУРЫ РАВНОВЕСИЯ ВРАЩАЮЩЕЙСЯ ЖИДКОСТИ Вкратце остановимся на проблеме фигур равновесия вращающейся жидкости, в разработку которой основной вклад внес А.М. Ляпунов.Ньютон показал, что под влиянием центробежных сил и взаимного притяжения своих частиц однородная
1. Понятие химического равновесия. Закон действующих масс
1. Понятие химического равновесия. Закон действующих масс При протекании химической реакции через некоторое время устанавливается химическое равновесие. Существует два признака химического равновесия: кинетический, термодинамический. В кинетическом – ?пр = ?обр, в
5. Расчет равновесного состава химического равновесия
5. Расчет равновесного состава химического равновесия Равновесный состав можно рассчитать только для газовой системы равновесная концентрация.Исходная концентрация всех компонентов Изменение каждого компонента по числу молей (или стехиометрическому
Рядовая звезда — Солнце
Рядовая звезда — Солнце «…Солнце является единственной звездой, у которой все явления могут быть детально изучены», — писал американский астроном Джордж Эллери Хейл, получивший золотую медаль Королевского астрономического общества за метод фотографирования
84 Как отличить подделку, или О состоянии вещества
84 Как отличить подделку, или О состоянии вещества Для опыта нам потребуются: кусочек янтаря или канифоли, кусочек пластмассы, иголка. Есть сложные способы отличить состав вещества, обычно это уже даже не физика, а химия. Определить, из чего состоит вещество, часто бывает
Глава 6
Глава 6 Тюрьма, со слепыми, без единого окна, стенами, размещалась глубоко в недрах облака, на котором была построена Белая Столица. Оказавшись в камере, напуганные Тристам и Том какое-то время молча сидели на кровати, отведенной им на двоих, — в действительности это были
Глава 7
Глава 7 Прошло несколько часов. Тристам и Том лежали на жестких нарах в темной камере без окон, непрестанно ворочаясь с боку на бок. Лишь только напев флейты смолк, старик сразу задремал, что-то неразборчиво бормоча во сне.Тома снова начало знобить; Тристама же разбирал
Глава 8
Глава 8 С прохладным и сыроватым рассветным воздухом смешивался густой дым, валивший из печных труб. На всех перекрестках в центре Белой Столицы были расставлены люди снегобоя. Они походили не столько на стражей порядка, сколько на оккупационные войска.Тристам и Том в
Глава 9
Глава 9 Наступила ночь, за окнами стояла глубокая тишина. Тристам уснул. Рядом с ним, с раскрытой книгой на животе, спал, погруженный в грезы о будущем, Том.В глубине комнаты, растянувшись на матрасе, храпел один из полицейских. Второй сидел на лесенке, стоявшей теперь возле
Глава 10
Глава 10 Тристам внимательно следил за тенью. Она двигалась прямо на военный патруль.«Там ему не проскочить!» — забеспокоился Тристам.Но человек с рюкзаком, наверное, и сам это знал: он вскарабкался по стене и, словно черная кошка, перепрыгивая с крыши на крышу, за считанные
Глава 11
Глава 11 Наутро, как только мальчики проснулись, полицейские повели их вниз, в подземный ход. К счастью, в тесном тоннеле, по которому пришлось продвигаться гуськом, было чисто и сухо.— Долго еще? — спросил Тристам, когда они прошли метров десять.— Тс-с! — шепнул
Глава 12
Глава 12 Тристам толкнул дверь и остановился у порога. Прямо перед ним была лестница, которая шла на второй этаж; несколько ступенек вели вниз, к запертой на засов двери подвала. Слева была кухня, справа — большая гостиная, залитая ярким утренним светом.— Входи, Тристам
Глава 13
Глава 13 Когда в гостиную вошел Том, Тристам сидел на диване. Он повесил мамин кулон себе на шею, заправив кристалл под свитер, и смотрел на портрет Миртиль, лежавший перед ним на низеньком столике. Глаза Тристама блестели, как будто он только что плакал.— Ну и тип! —
Глава 14
Глава 14 Густой туман, соединявший в себе, казалось, все оттенки серого цвета, окутывал Тристама, Тома, лейтенанта и его бойцов. Они гуськом бежали по дороге, вившейся в узкой долине между двумя колоссальными облаками.Порывы ветра окатывали их мириадами мельчайших брызг,
Нейтронная звезда на орбите вокруг черной дыры
Нейтронная звезда на орбите вокруг черной дыры Волны исходили от нейтронной звезды, вращающейся вокруг черной дыры. Звезда весила в 1,5 раза больше Солнца, а черная дыра – в 4,5 раза больше Солнца, при этом дыра быстро вращалась. Образованный этим вращением