Глава 51 ВОЛНЫ
Глава 51
ВОЛНЫ
§ 1. Волна от движущегося предмета
§ 2. Ударные волны
§ 3. Волны в твердом теле
§ 4. Поверхностные волны
§ 1. Волна от движущегося предмета
Мы закончили количественный анализ волн, но посвятим еще одну дополнительную главу некоторым качественным оценкам различных явлений, связанных с волнами; для подробного анализа они слишком сложны. Волнами мы занимаемся уже на протяжении нескольких глав, поэтому предмет настоящей главы было бы вернее назвать «некоторые из более сложных явлений, связанных с волнами».
Первым объектом нашего обсуждения будет эффект, производимый источником волн, движущимся со скоростью, превышающей скорость распространения волн, т. е. быстрее их фазовой скорости. Рассмотрим сначала волны, которые, подобно звуку или свету, имеют определенную постоянную скорость. Если источник звука движется со сверхзвуковой скоростью, то произойдет нечто вроде следующего. Пусть в данный момент источник, находящийся в точке x1, порождает звуковую волну (фиг. 51.1), тогда в следующий момент источник переместится в точку х2, а волна из точки х1распространится в радиусе r1, который меньше расстояния, пройденного источником, а из точки х2, разумеется, пойдет другая волна.
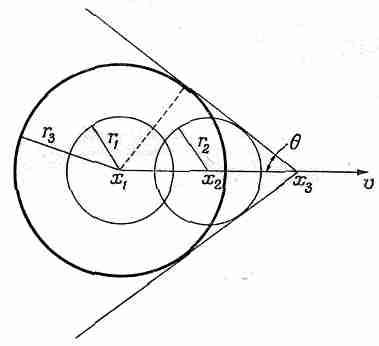
Фиг. 51.1. Фронт ударной волны, образующий конус с вершиной в источнике и углом полураствора q=arcsin(cw/v).
Когда источник переместится еще дальше, в точку х3, и отсюда тоже пойдет волна, то волна из точки х2 распространится в радиусе r2, а волна из точки х1— в радиусе r3. Конечно, все это происходит непрерывно, а не какими-то этапами, и поэтому получается целый ряд таких волновых колец с общей касательной линией, проходящей через центр источника. Мы видим, что источник, вместо того чтобы порождать сферические волны, как это произошло бы, будь он неподвижен, порождает фронт, образующий в трехмерном пространстве конус или в двухмерном пару пересекающихся прямых линий. Из рисунка нетрудно найти угол между этими двумя линиями. За данный отрезок времени источник проходит расстояние, пропорциональное его скорости v, скажем х3-х1 . Тем временем фронт волны распространится на расстояние r3, пропорциональное cw— скорости волны. Ясно поэтому, что синус угла полураствора равен отношению скорости волны к скорости источника, а это может быть только тогда, когда cwменьше v, или скорость объекта больше скорости волны:
sinq=cw/v. (51.1)
Интересно, что движущийся предмет вовсе не обязан быть источником звука, оказывается, что когда предмет движется быстрее скорости звука, то он сам производит звук. Ему для этого вовсе не обязательно вибрировать. Любой предмет, движущийся через среду быстрее, чем эта среда переносит волны, будет автоматически порождать волны просто благодаря своему движению. Это проще понять для случая звука, но тоже самое происходит и со светом. Сначала может показаться, что ничто не может двигаться быстрее скорости света. Однако фазовая скорость света в стекле, например, меньше, чем в пустоте, а через кусок стекла можно пропустить такую частицу, скорость которой будет очень близка к скорости света в пустоте, тогда как фазовая скорость света в стекле может быть равна только 2/3 этой скорости. Частица, летящая быстрее света в среде, порождает коническую световую волну с вершиной в источнике, подобно волнам, вызванным лодкой (эти волны одной и той же природы). Измеряя угол при вершине конуса, мы можем определить скорость частицы. В физике это используется для измерения скорости частиц как один из методов определения их энергии при высокоэнергетических исследованиях. Единственное, что приходится измерять,— это направление излучения света.
Такое излучение называют излучением Черенкова, который первый наблюдал его. Тамм и Франк теоретически выяснили, насколько оно должно быть интенсивным. За эту работу этим ученым в 1958 г. совместно была присуждена Нобелевская премия.
Подобное же явление для случая звука показано здесь на фиг. 51.2; это фотография объекта, движущегося через газ со скоростью, превышающей скорость звука.
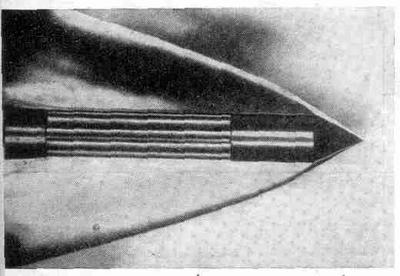
Фиг. 51.2. Ударная волна в газе, вызванная снарядом, движущимся быстрее звука.
Изменение в давлении приводит к изменению показателя преломления, поэтому границу волн с помощью специальной оптической системы можно сделать видимой. Итак, предмет, движущийся быстрее скорости звука, действительно дает коническую волну. Однако при более внимательном рассмотрении оказывается, что граница на самом деле искривлена. В асимптотике это действительно прямая линия, но вблизи вершины она искривлена, и сейчас мы обсудим, отчего так может получаться. Это непосредственно приводит нас ко второй теме данной главы.
§ 2. Ударные волны
Зачастую скорость волны зависит от ее амплитуды, и в случае звука эта зависимость возникает следующим образом. Движущийся в воздухе предмет должен сдвигать его со своего пути, вызывая при этом возмущение в виде какой-то ступенчатой функции давления, причем давление за волновым фронтом оказывается выше, чем в невозмущенной области, т. е. в области, куда волна (которая распространяется с нормальной скоростью) еще не добралась. Воздух за волновым фронтом оказывается адиабатически сжатым, поэтому температура его будет выше, чем перед фронтом. Но скорость звука с температурой увеличивается, поэтому в области позади скачка она оказывается больше скорости звука впереди него.
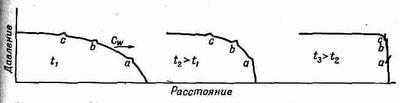
Это означает, что любое другое возмущение за скачком, вызванное, например, постоянным напором тела или чем-то другим, будет бежать быстрее, чем сам фронт: с увеличением давления скорость увеличивается. Эта картина показана на фиг. 51.3, причем для большей наглядности дополнительные возмущения взяты в виде небольших горбиков.
Фиг. 51.3. «Мгновенные снимки» ударного фронта в последовательные моменты времени.
Мы видим, что области высокого давления с течением времени «подгоняют» фронт волны, пока волна давления в конце концов не превратится в волну с резким фронтом. Если сила волны очень велика, то «в конце концов» означает — сразу же; если же волна довольно слабая, то это займет сравнительно много времени; обычно звук скорее рассеивается и замирает прежде, чем это превращение успеет произойти.
Давление, вызываемое звуком нашей речи, очень мало по сравнению с атмосферным — только одна миллионная часть или что-то в этом роде. Но при изменении давления на величину порядка 1 атм скорость волны увеличивается примерно на 20% и «заострение» фронта волны происходит соответственно быстрее. В природе, по-видимому, ничего не протекает бесконечно быстро и то, что мы называем «резким» фронтом, на самом деле имеет все же небольшую толщину; он не бесконечно крут. Расстояние, на котором все это происходит,— порядка средней длины свободного пробега молекулы, но на таких расстояниях волновое уравнение становится несправедливым, ведь при выводе его мы не учитываем молекулярной структуры газа.
Вернемся снова к фиг. 51.2. Мы видим, что кривизну легко объяснить, если понять, что давление вблизи вершины выше, чем вдали от нее, поэтому угол 0 здесь больше. Таким образом, кривизна возникла вследствие зависимости скорости от силы волны. Например, волна от взрыва атомной бомбы в течение некоторого времени движется гораздо быстрее звука, пока не отойдет достаточно далеко и в результате расплывания не будет ослаблена в такой степени, что перепад давления станет малым по сравнению с атмосферным. При этом скорость фронта приближается к скорости звука в газе, в котором он распространяется. (Скорость ударной волны всегда оказывается выше скорости звука в газе перед ней и ниже скорости звука в газе за ней. Таким образом, импульсы, идущие сзади, будут догонять фронт, но сам он движется в среде быстрее, чем нормальная скорость звукового сигнала. Поэтому только по звуку никто не в силах предсказать появление ударной волны, пока не становится слишком поздно. Конечно, свет от взрыва бомбы виден раньше, но предугадать приход ударной волны невозможно, никакого звукового сигнала впереди нее нет.)
Накапливание волн — очень интересное явление, и в основном причина его состоит в том, что после прохода одной волны скорость следующей за ней волны должна возрасти.
Рассмотрим еще один пример того же явления. Представьте себе длинный канал конечной ширины и глубины, заполненный водой. Если с достаточной быстротой двигать вдоль канала поршень, то вода будет собираться перед ним, как снег перед снегоочистителем. Теперь вообразите ситуацию, подобную изображенной на фиг. 51.4, когда где-то в канале вдруг возникает скачок высоты уровня воды
Фиг. 51.4. Падение воды и водовороты.
Можно показать, что длинные волны в канале идут быстрее по глубокой воде, чем по мелкой. Поэтому любой новый толчок или какие-то иные нерегулярности в энергии, поступающей от поршня, побегут вперед и соберутся на фронте волны. Теоретически мы снова в конце концов должны получить резкий фронт. Однако (см. фиг. 51.4) здесь возникают некоторые усложнения. Вы видите волну, идущую вверх по каналу, причем поршень находится где-то далеко с правой стороны канала. Сначала может показаться, что это хорошая волна, такая, какую и следует ожидать, но дальше она становится острее и острее, пока не произойдет то, что изображено на рисунке. Вода на поверхности начинает сильно бурлить и переливаться вниз, но, что самое существенное, край по-прежнему остается резким, и впереди него нет никакого возмущения.
В действительности волна на воде — вещь куда более сложная, чем звук. Однако для иллюстрации мы попытаемся проанализировать скорость так называемого высокого прилива в канале. Дело не в том, что это очень важно для наших целей (никакого обобщения здесь не будет), это только иллюстрация того, как законы механики, которые мы хорошо знаем, способны объяснить подобное явление.
Вообразите на минуту, что поверхность воды имеет такой вид, как изображено на фиг. 51.5,а, и что на верхнем уровне h2 она движется со скоростью v, а фронт со скоростью u надвигается на невозмущенную поверхность, высота которой h1. Мы хотим определить скорость, с которой движется фронт. За промежуток времени Dt вертикальная плоскость, проходившая вначале через точку x1передвинется на расстояние vDt, т. е. от х1до х2, а фронт волны пройдет расстояние uDt.
Применим теперь законы сохранения вещества и импульса. Возьмем сначала первый из них: мы видим, что на единицу ширины канала количество вещества h2vDt, прошедшее мимо точки x1 (область, заштрихованная на фиг. 51.5,6), компенсируется другой заштрихованной областью, представляющей количество вещества (h2-h1)uDt. Разделив на Dt, получим vh2=u(h2-h1). Но этого еще недостаточно, так как, хотя нам известны h1 и h2, мы еще не знаем ни u, ни v, а хотим найти обе величины.
Следующим шагом будет использование закона сохранения импульса. Мы еще не касались вопросов давления в воде и прочей гидродинамики, но и так ясно, что давление в воде на какой-то глубине должно быть как раз достаточным, чтобы поддерживать столбик воды над этой глубиной. Следовательно, давление воды равно произведению плотности r на g и на глубину. Так как давление воды возрастает линейно с глубиной, то среднее давление на плоскость, проходящую, например, через точку х1, равно l/2rgh2, что также представляет среднюю силу на единичную ширину и на единичную длину, толкающую плоскость к точке х2. Чтобы получить полную силу, давящую на воду слева, мы должны еще раз умножить на h2. С другой стороны, давление на рассматриваемую область справа дает противоположно направленную силу, которая по тем же причинам равна ll2rgh21. Теперь мы должны приравнять эти силы к скорости изменения импульса. Таким образом, нам нужно выяснить, насколько в случае, изображенном на фиг. 51.5,6, импульс больше, чем в случае, показанном на фиг. 51.5,а.
Мы видим, что дополнительная масса, которая приобрела скорость v, равна просто rh2uDt—rh2vDt (на единицу ширины), а умножение ее на v дает дополнительный импульс, который должен быть приравнен к импульсу силы FDt:
(rh2uDt-rh2vDt)v=(1/2rgh22-1/2rgh21}Dt.
Исключая из этого уравнения v подстановкой vh2=и(h2-h1) и упрощая его, получаем окончательно u2=gh2(h1+h2)/2h1.
Если разность высот очень мала, так что h1и h2приблизительно одинаковы, то скорость будет равна Цgh. Как мы увидим позднее, это справедливо только при условии, что длина волны много больше глубины канала.
Аналогичную вещь можно сделать и для ударных волн, только теперь нужно добавить уравнение сохранения внутренней энергии, потому что ударная волна — явление необратимое. Действительно, если в задаче о высокой приливной волне проверить закон сохранения энергии, то мы увидим, что он не выполняется. Когда разность высот мала, то энергия почти сохраняется, но как только разность высот становится более заметной, возникают большие потери. Это проявляется в падении воды и водоворотах, показанных на фиг. 51.4.
С точки зрения адиабатического процесса в ударной волне тоже происходит аналогичная потеря энергии. Энергия в звуковой волне за ударным фронтом уходит на нагревание газа, что соответствует бурлению воды при высоком приливе. Оказывается, что необходимо решить три уравнения, чтобы описать все это для случая звука, причем нужно учесть, что температура за ударной волной и перед ней, как мы видели, не одинакова.
Если мы попытаемся пустить высокий прилив в обратную сторону (h2<h1), то окажется, что потеря энергии отрицательна.
Но поскольку энергию взять неоткуда, высокий прилив не может поддерживать сам себя — он не стабилен. Если попытаться создать волну такого вида, то дальше она становится все более и более плоской, ведь зависимость скорости от высоты, которая раньше давала резкий фронт, в нашем случае будет работать в обратную сторону.
§ 3. Волны в твердом теле
Следующий тип волн, о которых нам следует поговорить,— это волны в твердом теле. Мы уже рассмотрели звуковые волны в жидкости и газе, а между ними и звуковыми волнами в твердом теле имеется непосредственная аналогия. Если резко толкнуть твердое тело, то оно сожмется. Оно сопротивляется сжатию и в нем возникнут волны, аналогичные звуковым. Однако в твердом теле могут быть волны и другого рода, которых не бывает в жидкости. Если мы возбудим колебания твердого тела с помощью бокового давления (это называется сдвигом), то тело стремится вернуться в начальное положение. Именно этим, по определению, твердое тело отличается от жидкого. Если искривить жидкость и подержать ее так немного, чтобы она успокоилась, а затем отпустить, то она останется в том же состоянии, но если мы возьмем твердое тело, похожее на дрожащий кусок желе, надавим на него и отпустим, то оно вернется назад, а в теле возникает волна сдвига, которая распространяется так же, как и волна сжатия. Во всех случаях скорость этих волн меньше скорости продольных волн. В каком-то отношении волны сдвига больше напоминают световые волны, ибо здесь мы тоже имеем дело с поляризацией. У звука нет никакой поляризации, это просто волна сжатия, а световые колебания имеют характерную ориентацию, перпендикулярную к направлению их распространения.
Итак, в твердом теле могут быть волны обоих сортов. Во-первых, там распространяются волны сжатия, аналогичные звуку в воздухе, и, во-вторых, волны сдвига. Если наше твердое тело не кристалл, то волна сдвига может быть поляризована в любом направлении. (Конечно, все твердые тела — кристаллы, но если мы возьмем кусок, состоящий из микрокристаллов всех ориентации, то кристаллическая анизотропия усредняется.)
Есть еще один интересный вопрос, касающийся звуковых волн. Что получится, если длина волны в твердом теле становится все меньше и меньше? До каких пор может это продолжаться? Ясно, что она не может стать меньше расстояния между атомами, ибо если под волной мы понимаем такое явление, когда одна точка идет вниз, а следующая — вверх и т. д., то кратчайшая возможная длина волны при этом, очевидно, равна межатомному расстоянию. Вам известно, что колебания могут быть как продольные, так и поперечные, длинноволновые и коротковолновые.
Если мы рассматриваем длины волн, сравнимые с межатомным расстоянием, то скорость уже не будет постоянной; возникает дисперсионный эффект, когда скорость становится зависимой от волнового числа. А высшая гармоника поперечных волн все же должна характеризоваться именно тем, что каждые два соседних атома делают нечто противоположное друг другу.
С атомистической точки зрения ситуация здесь напоминает два связанных маятника, о которых мы уже говорили. У них могут быть два вида собственных колебаний: один — когда они качаются вместе, и другой — когда в противоположные стороны. Так что волны в твердом теле можно рассматривать и с иной точки зрения — как колебания связанных гармонических осцилляторов, подобных огромному числу связанных маятничков, причем высшая гармоника получается, когда маятнички колеблются в противоположные стороны, и низшие — при других соотношениях фаз.
Эти кратчайшие волны настолько малы, что обычно их невозможно получить технически. Однако они очень интересны, поскольку свойства этих коротких звуковых волн помогают нам объяснить в термодинамической теории твердого тела его тепловые свойства, в частности удельную теплоемкость. Переход к предельно коротким звуковым волнам означает переход к индивидуальному движению атомов; это в конечном счете одно и то же.
Очень интересным примером звуковых волн в твердом теле являются волны, идущие по земному шару, как продольные, так и поперечные. Хотя нам и не известно почему, но внутри Земли время от времени происходят землетрясения. Одни породы сдвигаются относительно других, и это движение сходно с очень низким звуком. Из такого источника выходят и путешествуют по всей Земле волны, подобные звуковым, и хотя их длина значительно больше длины обычных звуковых волн, но все же это звуковые волны. Наша Земля не однородна: давление, плотность, сжимаемость и т. д. изменяются с изменением глубины, а поэтому изменяется и скорость. Возникает нечто похожее на показатель преломления, и волны идут не по прямому пути, а по некоторой кривой. Кроме того, картина осложняется тем, что продольные и поперечные волны распространяются с разной скоростью, а поэтому и решения для них будут разными. Если мы в каком-то месте поставим сейсмограф и будем наблюдать, как скачет его самописец после того, как где-то произошло землетрясение, то мы увидим не просто какие-то неправильные прыжки. Мы увидим, как самописец сначала запрыгает, затем успокоится, затем опять запрыгает. Более конкретные детали происходящего зависят от положения сейсмографа. Если он расположен достаточно близко к месту землетрясения, то сначала мы примем продольные волны от возмущения, а уж потом, несколько секунд спустя,— поперечные, ибо они идут медленней. Измеряя разницу времени между их приходами, можно сказать, насколько далеко произошло землетрясение, разумеется, если мы достаточно хорошо знаем скорости и состав внутренних областей.
На фиг. 51.6 показан пример поведения различных видов волн в Земле.
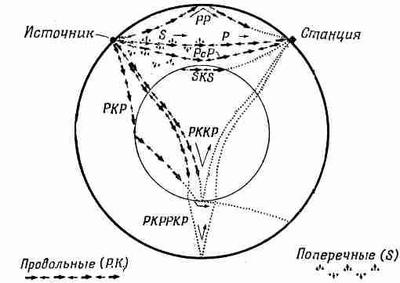
Фиг. 51.6. Схема земного шара.
Показаны пути продольных и поперечных звуковых волн.
Два сорта волн обозначены различными значками. Если в каком-то месте (назовем его «источник») произошло землетрясение, то поперечные и продольные волны, идущие по прямому пути, придут на станцию в разные моменты времени. Кроме того, возникнут отражения от границ неоднородности, дающие в результате другие пути и времена. Подобные исследования показали, что у Земли есть некое ядро, не проводящее поперечных волн. Однако даже если станция расположена диаметрально противоположно источнику, то поперечные волны все же приходят, но с неправильной фазой. Это получается оттого, что поперечные волны, падающие наклонно на поверхность, разделяющую два вещества, всегда рождают две новые волны: поперечную и продольную. Но внутри ядра Земли поперечные волны не распространяются (по крайней мере в отличие от продольных волн для них этого не обнаружено). Затем на границе ядра оба вида волн возникают вновь и попадают на станцию.
Именно по поведению волн, вызванных землетрясениями, было обнаружено, что поперечные волны не могут распространяться в некоторой сфере внутри Земли. Это означает, что центр Земли жидкий в том смысле, что он не проводит поперечных волн. Изучение землетрясений — это единственный источник наших сведений о внутреннем строении Земли. Таким образом, в результате большого числа наблюдений на различных станциях в период многих землетрясений были выяснены все детали; известно все: скорости, кривые и т. д. Мы знаем скорости различных сортов волн на любой глубине. А зная это, мы, следовательно, можем выяснить, каковы собственные гармоники Земли, ибо нам известна скорость распространения звуковых волн: другими словами, известны упругие свойства на любой глубине. Предположим, что мы приплюснули земной эллипсоид и затем отпустили его. Задача определения периода и формы свободных колебаний сводится просто к вопросу о суперпозиции волн, идущих по эллипсоиду. Мы уже выяснили, что при подобном возмущении возникает множество гармоник, начиная от низшей, которая для Земли эллипсоидальна, и вплоть до более высоких и более сложных.
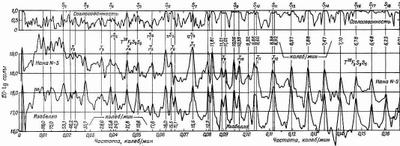
Чилийское землетрясение в мае 1960 г. произвело такой «шум», что его эхо много раз обошло вокруг Земли. Как раз к этому времени были изготовлены новые высокочувствительные сейсмографы, с помощью которых определялись основные гармоники Земли и сравнивались с величинами, вычисленными из теории звука по известным скоростям, найденным из других независимых землетрясений. Результат этого эксперимента показан на фиг. 51.7, где отложена сила сигнала в зависимости от его частоты (фурье-анализ).
Фиг. 51.7. Зависимость силы от частоты, зарегистрированная сейсмографом в городах Нака (Перу) и Изабелла (Калифорния).
Согласованность (или когерентность) обозначает степень связанности сигналов, регистрируемых этими станциями.
Заметьте, что одни из принимаемых частот оказывались более сильными, чем другие; наблюдались очень четкие максимумы. Это и есть собственные частоты Земли, поскольку они являются главными частотами ее колебаний.
Иными словами, если все движение Земли сводится к суперпозиции множества различных гармоник, то можно надеяться, что запись нерегулярных толчков на любой станции даст одну и ту же суперпозицию многих частот. Если проанализировать это в терминах частот, то мы сможем определить характеристические частоты Земли. Тонкие вертикальные линии на рисунке изображают рассчитанные частоты, и мы видим замечательное согласие, убеждающее нас, что теория звука вполне работает и внутри Земли.
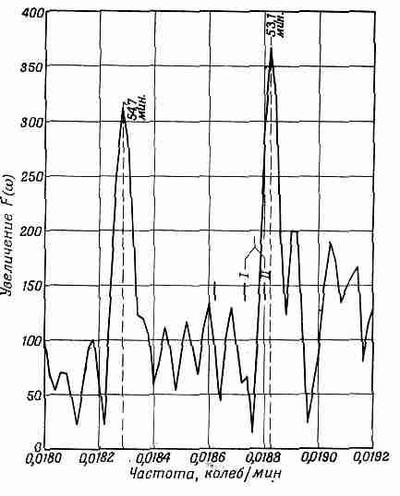
Очень интересный факт обнаруживается на фиг. 51.8, где представлены очень точные измерения (с еще большим разрешением) низшей эллипсоидальной гармоники.
Фиг. 51.8.Фурье-анализ записи высокочувствительного сейсмографа на станции Изабелла. Хорошо виден спектральный дублет.
Заметьте, что здесь не один, а два немного отличающихся максимума: первый — с периодом 54,7 мин и второй — 53,1 мин. Природа этих двух максимумов не была известна, когда они были обнаружены, хотя с тех пор ее могли найти. Существуют по крайней мере два правдоподобных объяснения. Одно из них — это возможная асимметрия в распределении вещества Земли, которая может дать два подобных максимума. Другое, еще более интересное объяснение состоит в следующем. Вообразите волны, идущие от источника вокруг Земли в двух направлениях. Если мы в уравнениях движения учтем эффект вращения Земли, которым обычно пренебрегали при анализе, то скорости этих волн окажутся разными. Движение во вращающейся системе из-за действия кориолисовой силы изменяется, и это может вызвать наблюдаемое расщепление.
Коротко о методе получения этих кривых. На сейсмографе мы записываем не зависимость амплитуды от частоты, а перемещение как функцию времени, причем всегда какой-то очень неправильной и причудливой формы.
Чтобы найти из нее долю различных синусообразных волн для всех частот, мы уже знаем, что нужно делать. Фокус состоит в умножении полученных данных на синусообразную волну данной частоты и интегрировании, т. е. усреднении; при этом усреднении все другие частоты исчезают.
Таким образом, на рисунках фактически показаны графики интегралов от произведения полученных данных на синусообразные волны с различным числом периодов в минуту.
§ 4. Поверхностные волны
Следующий интересный тип волн, которые, несомненно, видел каждый и которые обычно в элементарных курсах служат примером волн,— это волны на поверхности воды. Вы скоро убедитесь, что более неудачного примера придумать трудно, ибо они нисколько не похожи ни на звук, ни на свет; здесь собрались все трудности, которые только могут быть в волнах. Давайте начнем с длинных волн на глубокой воде. Если считать океан бесконечно глубоким и на его поверхности происходят какие-то возмущения, то возникнут волны. Вообще говоря, возможны любые возмущения, но синусоидальное движение с очень небольшим возмущением дает волны, напоминающие обычные гладкие океанские волны, идущие к берегу. Вода, разумеется, в среднем остается на месте, а движутся сами волны. Что ж это за движение — поперечное или продольное? Оно не может быть ни тем, ни другим: ни поперечным, ни продольным. Хотя в каждом данном месте горбы чередуются со впадинами, оно не может быть движением вверх и вниз просто из-за закона сохранения количества воды. Куда должна деваться вода из впадины? Ведь она же практически несжимаема. Скорость волн сжатия, т. е. звука в воде, во много раз больше: мы сейчас их не рассматриваем. Итак, для нас сейчас вода несжимаема, поэтому при образовании впадины вода из этого места может двигаться только в стороны. Так оно и получается на самом деле: частички воды вблизи поверхности будут двигаться приблизительно по окружности. Как-нибудь, когда вы будете нежиться на воде, лежа на круге, и придет такой гладкий вал, посмотрите на соседние предметы и вы увидите, что они движутся по окружностям. Так что картина получается неожиданная: здесь мы имеем дело со смесью продольных и поперечных волн. С увеличением глубины круги уменьшаются, пока на достаточной глубине от них ничего не останется (фиг. 51.9).
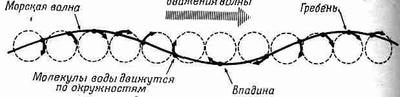
Фиг. 51.9. Волны, на глубокой воде образуются частицами, движущимися по окружности.
Обратите внимание на систематический сдвиг фазы от одной окружности к другой. Кок может при этом двигаться плавающий предмет?
Очень интересно определить скорость таких волн. Это должно быть какой-то комбинацией плотности воды, ускорения силы тяжести, которая в данном случае является восстанавливающей силой, и, возможно, длины волны и глубины. Если мы рассмотрим случай бесконечной глубины, то скорость больше не будет зависеть от нее. Но какую бы формулу для фазовой скорости волн мы ни взяли, она должна содержать эти величины в такой комбинации, чтобы давать правильную размерность. Испробовав множество различных способов, мы найдем, что только одна комбинация g и l может дать нам размерность скорости, именно Цgl, которая совсем не включает плотности. На самом деле эта формула для фазовой скорости не вполне точна, и полный анализ динамики, в который мы не будем входить, показывает, что все действительно получится так, как у нас, за исключением Ц2p, т. е.
vфаз=Цgl/2p (для волн «тяжести»).
Интересно, что длинные волны бегут быстрее коротких. Так что когда проходящая вдали моторная лодка создает волны, то после некоторого промежутка времени они достигнут берега, но сначала это будут редкие всплески, поскольку первыми приходят длинные волны. Затем приходящие волны становятся все короче и короче, ибо скорость падает как квадратный корень из длины волны.
«Это же неверно,— может возразить кто-нибудь,— ведь чтобы делать такое утверждение, мы должны смотреть на групповую скорость». Правильно, конечно. Формула для фазовой скорости не говорит нам о том, что приходит первым; об этом может нам сказать только групповая скорость. Так что мы должны получить групповую скорость и мы сможем показать, что она равна половине фазовой скорости. Для этого нужно только вспомнить, что фазовая скорость ведет себя как квадратный корень из длины волны. Так же, т. е. как квадратный корень из длины волны, ведет себя и групповая скорость. Но как может групповая скорость быть вдвое меньше фазовой? Посмотрите на группу волн, вызванных проходящей мимо лодкой, и проследите за каким-то определенным гребнем. Вы обнаружите, что он бежит вместе с группой, но постепенно становится все меньше и меньше, а дойдя до переднего фронта, совсем умирает. Но таинственным и непостижимым образом на смену ему с заднего фронта поднимается слабенькая волна и становится она все сильнее и сильнее. Короче говоря, по группе движутся волны, тогда как сама группа движется вдвое медленнее этих волн.
Поскольку групповая и фазовая скорости не равны друг другу, то волны, вызванные движущимся объектом, будут уже не просто коническими, а гораздо более сложными и интересными. Вы можете видеть это на фиг. 51.10, где показаны волны, вызванные движущейся по воде лодкой.

Фиг. 51.10. След прошедшей моторной лодки.
Заметьте, что они совсем не похожи на то, что мы получали для звука (когда скорость не зависит от длины волны), где фронт волны был просто распространяющимся в стороны конусом. Вместо него мы получили волны позади движущегося объекта, фронт которых перпендикулярен его движению, да еще движущиеся под другими углами небольшие волны с боков. Всю эту картину движения волн в целом можно очень красиво воссоздать, зная только, что фазовая скорость пропорциональна квадратному корню из длины волны. Весь фокус заключается в том, что картина волн стационарна относительно лодки (движущейся с постоянной скоростью); все другие виды волн отстанут от нее.
До сих пор мы рассматривали длинные волны, для которых восстанавливающей силой была сила тяжести. Но когда волны становятся очень короткими, то основной восстанавливающей силой оказывается капиллярное притяжение, т. е. энергия поверхностного натяжения. Для волн поверхностного натяжения фазовая скорость равна
vфаз=Ц2pT/lr(для ряби),
где Т — поверхностное натяжение, а r — плотность. Здесь все наоборот: чем короче длина волн, тем большей оказывается фазовая скорость. Если же действуют и сила тяжести и капиллярная сила, как это обычно бывает, то мы получаем комбинацию
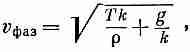
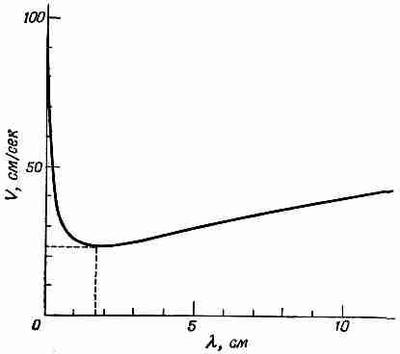
где k=2p/l — волновое число. Как видите, скорость волн на воде — вещь действительно довольно сложная. На фиг. 51.11 показана фазовая скорость как функция длины волны.
Фиг. 51.11. График зависимости фазовой скорости от длины волны для воды.
Она велика для очень коротких волн, велика для очень длинных волн, но между ними существует некоторая минимальная скорость распространения. Исходя из этой формулы, можно вычислить и групповую скорость: она оказывается равной 3/2 фазовой скорости для ряби и 1/2 фазовой скорости для волн «тяжести». Слева от минимума групповая скорость больше фазовой, а справа групповая скорость меньше. С этим фактом связано несколько интересных явлений. Поскольку групповая скорость с уменьшением длины волны быстро увеличивается, то, если мы создадим какие-то возмущения, возникнут волны соответствующей длины, которые идут с минимальной скоростью, а впереди них с большей скоростью побегут короткие и очень длинные волны. В любом водоеме можно легко увидеть очень короткие волны, а вот длинные волны наблюдать труднее.
Таким образом, мы убедились, что рябь, которая столь часто используется для иллюстрации простых волн, на самом деле гораздо сложнее и интереснее: у нее нет резкого волнового фронта, как в случае простых волн, подобных звуку или свету. Основная волна, которая вырывается вперед, состоит из мелкой ряби. Благодаря дисперсии резкое возмущение поверхности воды не приводит к резкой волне. Первыми все равно идут очень мелкие волны. Во всяком случае, когда по воде с некоторой скоростью движется объект, то возникает очень сложная картина, поскольку разные волны идут с разной скоростью. Взяв корыто с водой, можно легко продемонстрировать, что самыми быстрыми будут мелкие капиллярные волны, а уже за ними идут более крупные. Кроме того, наклонив корыто, можно увидеть, что там, где меньше глубина, меньше и скорость. Если волна идет под каким-то углом к линии максимального наклона, то она заворачивает в сторону этой линии. Таким способом можно продемонстрировать множество различных вещей и прийти к заключению, что волны на воде — куда более сложная вещь, чем волны в воздухе.

Скорость длинных волн с круговым движением воды уменьшается на мелком месте и увеличивается на глубоком. Таким образом, когда волна идет к берегу, где глубина меньше, она замедляется. Но там, где вода глубже, волна движется быстрее, так что мы снова сталкиваемся с механизмом ударной волны. Однако на этот раз, поскольку волна не столь проста, ударный фронт ее гораздо больше искажен: волна «перегибается через себя» самым привычным для нас образом (фиг. 51.12).
Фиг. 51.12. Морская волна.
Именно это мы видим, когда волна набегает на берег: в ней выявляются все присущие природе трудности. Никому до сих пор не удалось вычислить форму волны в тот момент, когда она разбивается. Это очень легко сделать, когда волны малы, но когда они становятся большими, все слишком усложняется.
Интересное свойство капиллярных волн можно наблюдать при возмущении поверхности движущимся объектом. С точки зрения самого объекта вода течет мимо него, и волны, которые в конечном итоге останутся вместе с ним, всегда будут волнами, которые как раз имеют нужную скорость, чтобы оставаться на воде вместе с объектом. Точно так же если поместить объект в поток, который будет омывать его, то картина волн окажется стационарной и как раз нужной длины волны для того, чтобы двигаться с той же скоростью, что и вода. Но если групповая скорость меньше фазовой, то возмущение идет по потоку назад, поскольку групповая скорость недостаточна для того, чтобы догнать поток. Если же групповая скорость больше фазовой, то волновая картина появится перед объектом. Если пристально следить за плывущим в потоке объектом, то можно заметить впереди него небольшую рябь, а позади него — длинные волны.
Другие интересные явления подобного рода можно наблюдать в льющейся жидкости. Если, например, быстро выливать молоко из бутылки, то можно заметить, как струя молока пересекается множеством перекрещивающихся линий. Это волны, вызванные возмущением на краях бутылки; они очень похожи на волны, вызванные объектом, плывущим по потоку. Но теперь такой эффект возникает с обеих сторон, поэтому получается картина пересекающихся линий.
Итак, мы познакомились с некоторыми интересными свойствами волн, с различными усложнениями, зависящими от фазовой скорости и длины волны, а также с зависимостью скорости волны от глубины и т. д.; все это приводит к весьма сложным, а потому и интересным явлениям природы.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
Продольны или поперечны световые волны?
Продольны или поперечны световые волны? Все рассмотренные нами оптические явления говорят в пользу волновой теории. Искривление луча света у краев малых отверстий и препятствий и объяснение преломления — это самые сильные аргументы в ее пользу. Руководствуясь
Волны материи
Волны материи Как истолковать тот факт, что в спектрах элементов оказываются лишь определенные характерные длины волн?В физике часто случалось, что существенный успех был достигнут проведением последовательной аналогии между не связанными по виду явлениями. В этой
Волны вероятности
Волны вероятности Согласно классической механике, если мы знаем положение и скорость данной материальной точки, а также внешние действующие силы, мы можем предсказать на основе законов механики весь ее будущий путь. В классической механике утверждение «Материальная
Волны на поверхности воды
Волны на поверхности воды Каждый знает, что водяные волны бывают разные. На поверхности пруда едва заметная зыбь слегка качает пробку рыболова, а на морских просторах огромные водяные валы раскачивают океанские пароходы. Чем же отличаются волны друг от друга?Посмотрим,
Электромагнитные волны
Электромагнитные волны В то же время, когда спектроскопия начала так бурно развиваться, английский физик Джемс Клерк Максвелл (1831 —1879) обобщал результаты опытных исследований электрических и магнитных свойств материи. При этом он вовсе не имел дела со светом и со всеми
Длина волны электромагнитных волн
Длина волны электромагнитных волн Но там, где есть периодическое колебание, которое распространяется в пространстве, там можно говорить и о длине волны. У водяных волн мы называли длиной волны расстояние между двумя ближайшими гребнями. А что такое гребень водяной волны?
Глава 24 Черные дыры и гравитационные волны
Глава 24 Черные дыры и гравитационные волны Основоположник теории внутреннего строения звезд выдающийся английский ученый А. С. Эддингтон был, как известно, крупнейшим знатоком общей теории относительности. Он впервые во время солнечного затмения в 1919 г. измерил
Глава 10 Гравитационные волны
Глава 10 Гравитационные волны А синуса график волна за волной На ось ординат набегает. Студенческая песня Электромагнитные волны Развивая рассказ о создании новой теории гравитации ОТО, мы все время возвращались к идеям Ньютона и результатам его теории. Сейчас,
Электромагнитные волны
Электромагнитные волны Развивая рассказ о создании новой теории гравитации ОТО, мы все время возвращались к идеям Ньютона и результатам его теории. Сейчас, начиная рассказ о гравитационных волнах, мы нарушим эту традицию и обратимся к электромагнетизму Максвелла.
140. Что такое гравитационные волны?
140. Что такое гравитационные волны? Гравитационные волны являются гипотетическими волнами в структуре пространства-времени, движущимися со скоростью света, как рябь на поверхности пруда.Согласно общей теории относительности Эйнштейна, жесткое 4-мерное
Волны, идущие по поверхности
Волны, идущие по поверхности Подводники не знают морских бурь. В самые сильные штормы на глубине в несколько метров под уровнем моря царит штиль. Морские волны – один из примеров волнового движения, захватывающего лишь поверхность тела.Иногда может показаться, что
Волны и качка
Волны и качка Волны на море, бросающие корабль, то вздымающие его высоко на гребень, то погружающие в глубокую водяную долину, кажутся нам огромной высоты – выше многоэтажного дома. Однако это заблуждение: волны вовсе не так высоки, как кажется пассажиру корабля. Самые
Гравитационные волны
Гравитационные волны В 1919 г. Эйнштейн предсказал, что движущиеся массы производят гравитационные волны, распространяющиеся со скоростью света. К сожалению, амплитуда такого гравитационного излучения, испускаемого любым источником, созданным в лаборатории, слишком
16. Обнаружение червоточины: гравитационные волны
16. Обнаружение червоточины: гравитационные волны Как люди в «Интерстеллар» могли обнаружить червоточину? У меня как физика есть любимая версия, о которой я сейчас поведаю, выйдя за рамки непосредственных событий «Интерстеллар». Разумеется, эта лишь мои догадки,
Глава 16. Обнаружение червоточины: гравитационные волны
Глава 16. Обнаружение червоточины: гравитационные волны Свежая информация о проекте ЛИГО и поиске гравитационных волн – на сайте научного коллектива ЛИГО ligo.org (в особенности см. разделы News и Magazine) и на сайте лаборатории ЛИГО ligo.caltech.edu; также см. фильм Кая Стаатса