Глава 46 ХРАПОВИК И СОБАЧКА

Глава 46

ХРАПОВИК И СОБАЧКА

§ 1. Как действует храповик

§ 2. Храповик как машина

§ 3. Обратимость в механике

§ 4. Необрати­мость

§ 5. Порядок и энтропия

§ 1. Как действует храповик

В этой главе мы поговорим о храповике и собачке — очень простом устройстве, позволяю­щем оси вращаться только в одном направлении. Возможность получать одностороннее вращение заслуживает глубокого и тщательного анализа, из него проистекут интересные заключения.

Вопросы, которые мы будем обсуждать, воз­никают при попытке найти с молекулярной или кинетической точки зрения простое объяснение тому, что существует предел работы, которая мо­жет быть получена от тепловой машины. Правда, мы уже знаем сущность доказательства Карно, но было бы приятно найти и элементарное его объяснение — такое, которое показало бы, что так физически на самом деле происходит. Суще­ствуют, конечно, сложные, покоящиеся на зако­нах Ньютона математические доказательства ограниченности количества работы, которое можно получить, когда тепло перетекает с од­ного места в другое; но очень непросто сделать эти доказательства элементарными. Короче говоря, мы не понимаем их, хотя можем просле­дить выкладки.

В доказательстве Карно то обстоятельство, что при переходе от одной температуры к дру­гой нельзя извлечь неограниченное количество тепла, следует из другой аксиомы: если все происходит при одной температуре, то тепло не может быть превращено в работу посредством циклического процесса. Поэтому первым делом попытаемся понять, хотя бы на одном элементар­ном примере, почему верно это более простое утверждение.

Попробуем придумать такое устройство, что­бы второй закон термодинамики нарушался, т. е. чтобы работу из теплового резервуара получали, а перепада температур не было. Пусть в сосуде находится газ при некоторой тем­пературе, а внутри имеется вертушка (фиг. 46.1), причем будем считать, что T₁=T₂=T.

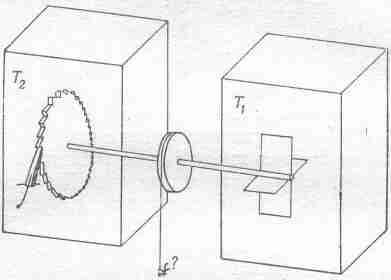
Фиг. 46.1. Машина, состоящая из храповика и собачки.

От ударов молекул газа вертушка будет покачиваться. Нам остается лишь пристроить к другому концу оси колесико, которое может вертеться только в одну сторону,— храповичок с собачкой. Собачка пресечет попытки вертушки поворачиваться в одну сторону, а повороты в другую—разрешит. Колесико будет медленно поворачиваться; может быть, удастся даже подвесить на ниточку блошку, привязать нить к барабану, насаженному на ось, и поднять эту блошку!

Возможно ли это? По гипотезе Карно — нет. Но по первому впечатлению — очень даже возможно (если только мы верно рас­судили). Видно, надо посмотреть повнимательнее. И действи­тельно, если вдумаешься в работу храповика с собачкой, все оказывается не так просто.

Во-первых, хотя наш идеализированный храповик и пре­дельно прост, но есть еще собачка, а при ней положено быть пружинке. Проскочив очередной зубец, собачка должна воз­вратиться в прежнее положение, так что без пружинки не обой­тись.

Весьма существенно и другое свойство храповика и собачки (на рисунке его нельзя показать). Предположим, что части наше­го устройства идеально упруги. Когда собачка пройдет через ко­нец зубца и сработает пружинка, собачка ударится о колесико и начнет подпрыгивать. Если в это время произойдет очередная флуктуация, вертушка может повернуться и в другую сторону, так как зубец может проскользнуть под собачкой, когда та приподнята! Значит, для необратимости вертушки важно, чтобы было устройство, способное гасить прыжки собачки. Но при этом гашении энергия собачки перейдет к храповику и примет вид тепловой энергии. Выходит, что по мере вращения храповик будет все сильнее нагреваться. Для простоты пусть газ вокруг храповика уносит часть тепла. Во всяком случае, вместе с хра­повиком начнет нагреваться и сам газ. И что же, так будет про­должаться вечно? Нет! Собачка и храповик, сами обладая неко­торой температурой Т, подвержены также и броуновскому дви­жению. Это значит, что время от времени собачка случайно поднимается и проходит мимо зубца как раз в тот момент, когда броуновское движение вертушки пытается повернуть ее назад. И чем горячее предмет, тем чаще это бывает.

Вот отчего наш механизм не будет находиться в вечном дви­жении. Иногда от щелчков по крыльям вертушки собачка под­нимается и вертушка поворачивается. Но иногда, когда вертуш­ка стремится повернуть назад, собачка оказывается уже при­поднятой (из-за флуктуации движений этого конца оси) и храповик действительно поворачивает обратно. В итоге—чистый нуль. И совсем нетрудно показать, что, когда температура в обоих сосудах одинакова, в среднем вращения не будет. Будет, конечно, множество поворотов в ту или иную сторону, но чего мы хотим — одностороннего вращения,— тому не бывать.

Рассмотрим причину этого. Чтобы поднять собачку до верха зубца, надо проделать работу против натяжения пружинки. Назовем эту работу e; пусть q — угол между зубцами. Шанс, что система накопит достаточно энергии e, чтобы поднять собач­ку до края зубца, есть ехр(-e/kT). Но вероятность того, что собачка поднимется случайно, тоже есть ехр(-e/kT). Значит, сколько раз собачка случайно поднимется, давая храповику свободно повернуться назад, столько же раз окажется достаточ­но энергии, чтобы при прижатой собачке вертушка повернулась вперед. Выйдет равновесие, а не вращение.

§ 2. Храповик как машина

Пойдем дальше. Рассмотрим другой пример: температура вертушки T₁, а температура храповика Т₂; T₂меньше Т_{1. Т}ак как храповик холодный и флуктуации собачки сравнитель­но редки, ей теперь очень трудно раздобыть энергию e. Но из-за того, что вертушка горячая, она часто получает энергию e, и наше устройство начнет, как и задумано, вертеться в одну сторону.

Посмотрим-ка, удастся ли нам теперь поднимать грузы. Привяжем к барабану нить и привесим к ней грузик вроде нашей блошки. Пусть L будет момент, создаваемый грузом. Если мо­мент L не очень велик, наша машина груз поднимет, так как из-за броуновских флуктуации повороты в одну сторону веро­ятнее, чем в другую. Определим, какой вес мы сможем поднять, как быстро он будет подниматься и т. д.

Сперва рассмотрим движение вперед, для которого храповик и предназначен. Сколько энергии нужно занять у вертушки, чтобы продвинуться на шаг? Чтобы поднять собачку, нужна энер­гия e. Чтобы повернуть храповик на угол q против момента L, нужна энергия Lq. Всего нужно занять энергию e+Lq. Вероят­ность заполучить ее равна ехр[-(e+Lq)/kT₁. В действитель­ности дело не только в самой этой энергии, но и в том, сколько, раз в секунду она окажется в нашем распоряжении. Вероят­ность в секунду только пропорциональна ехр[-(e+Lq)/kT₁]; обозначим коэффициент пропорциональности 1/t (он в конце выкладок выпадет). После каждого шага вперед совершенная над грузом работа есть Lq. Энергия, взятая у вертушки, равна e+Lq. Энергией e наматывается нить, затем следует: щелк, щелк, клингенкланггеклунген..., и энергия переходит в тепло, Вся одолженная энергия идет на то, чтобы поднять блошку и собачку, которая потом падает и отдает тепло другой стороне (храповику).

Рассмотрим теперь случай обратного вращения. Что проис­ходит здесь? Чтобы храповик повернулся назад, надо лишь снабдить собачку такой энергией, чтоб ей хватило сил подняться и пропустить храповик. Эта энергия по-прежнему равна e. Вероятность (в пересчете на секунду) того, что собачка подни­мется на нужную высоту, теперь равна (1/t)ехр(-e/kT₂). (Множитель пропорциональности тот же, но в показателе стоит kT₂из-за того, что температура иная.) Когда это случается, т. е. зубчатка проскальзывает назад, работа уже высвобождается (высвободился один зубец, а вместе с ним и работа Lq). Энергия, взятая у системы храповик — собачка, есть e, а энергия, пере­данная газу на другом конце оси при температуре T₁, есть Lq+e. Это тоже легко понять. Положим, что собачка поднялась сама собой за счет флуктуации. Когда она упадет и пружинка ударит ее по зубцу, возникнет сила, стремящаяся повернуть зубчатку, ведь плоскость-то, о которую ударилась собачка, наклонная. Эта сила производит работу; то же можно сказать о весе грузика. Обе силы суммируются, и вся медленно высво­бождаемая энергия появляется в виде тепла на той стороне, где вертушка. (Конечно, так и должно быть по закону сохра­нения энергии, но мы обязаны осторожно продумать все на­сквозь!)

Мы замечаем, что все эти энергии в точности те же, что и раньше, только переставлены. Итак, смотря по тому, какое из отношений больше, грузик либо медленно поднимается, либо медленно опускается. Конечно, на самом деле он непрерывно ходит туда-сюда, покачивается, но мы говорим об усредненном поведении.

Положим, что при определенном весе вероятности окажутся равными. Тогда привесим к нити бесконечно легкий грузик. Весь груз медленно пойдет вниз, и машина будет совершать работу, энергия будет откачиваться от храповика и пересылаться вертушке. Если же убрать часть груза, неравновесность переки­нется на другую сторону. Груз поднимается, тепло отбирается от вертушки и поставляется шестерне. Мы попадаем в условия обратимого цикла Карно благодаря тому, что груз выбран как раз так, чтобы обе вероятности были равны. Это условие таково: (e+Lq)/T₁=e/T₂. Пусть машина медленно тянет груз вверх.

Таблица 46.1 · ОПЕРАТИВНАЯ СВОДКА ДЕЙСТВИЙ ХРАПОВИКА И СОБАЧКИ

Энергия Q_lотбирается от лопастей, а энергия Q₂доставляется шестерне, и эти энергии находятся в отношении (e+Lq)/e. Когда мы опускаем груз, то опять Q₁/Q₂=(e+Lq)/e. Итак (табл. 46.1), мы имеем

Q₁/Q₂=T₁/T₂. Далее, полученная работа относится к энергии, взятой у вер­тушки, как Lq к Lq+e, т. е. как (T₁-Т₂)/Т₁. Мы видим, что наше устройство, работая обратимо, ни за что не сможет высо­сать работы больше, чем позволяет это отношение. Это тот вывод, которого мы и ожидали на основе доказательства Карно, а од­новременно и главный результат этой лекции.

Однако мы можем использовать наше устройство, чтобы по­нять еще кое-какие явления, даже неравновесные, лежащие вне области применимости термодинамики.

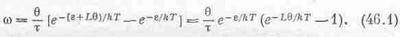
Давайте подсчитаем теперь, как быстро наш односторонний механизм будет вращаться, если все его части одинаково нагре­ты, а к барабану подвешен грузик. Если мы потянем чересчур сильно, могут произойти любые неприятности. Собачка соскользнет вдоль храповика, пружинка лопнет или еще что-нибудь случится. Но предположим, мы тянем так осторожно, что все работает гладко. В этих условиях верен вышеприведен­ный анализ вероятностей поворота храповика вперед или назад, и нужно только учесть равенство температур. С каждым скач­ком валик поворачивается на угол 9, так что угловая скорость равна величине 9, помноженной на вероятность одного из этих скачков в секунду. Ось поворачивается вперед с вероятностью (1/t)ехр[-e+Lq)/kT], а назад она поворачивается с вероят­ностью (1/t)ехр(-e/kT). Угловая скорость равна

График зависимости w от L показан на фиг. 46.2.

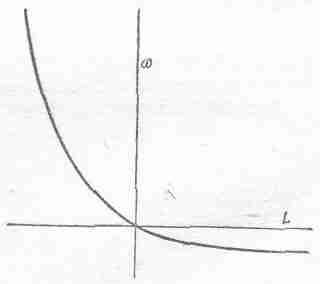
Фиг. 46.2. Угловая скорость храповика как функция враща­тельного момента.

Мы видим, что, когда L положительно, результат один, когда отрицательно — совсем другой. Если L растет, будучи положительным, что бывает, когда мы хотим повернуть храповик назад, скорость вра­щения назад близка к постоянной величине. А когда L стано­вится отрицательным, w поистине «рвется вперед», так как у e показатель степени огромен! Таким образом, угловая скорость, вызываемая действием разных сил, весьма несимметрична. Пойти в одну сторону легко: мы получаем большую угловую скорость от маленькой силы. Идя в обратную сторону, мы можем прило­жить много усилий, а вал все же будет двигаться еле-еле.

Такое же положение возникает в электрическом, выпрямите­ле. Вместо силы там имеется электрическое поле, а взамен угловой скорости — сила тока. Для выпрямителя напряжение тоже не пропорционально сопротивлению, наблюдается та же несимметричность. Анализ, проделанный нами для механиче­ского выпрямителя, годится и для электрического. Вид полу­ченной выше формулы типичен для зависимости пропускной способности выпрямителя от напряжения.

Уберем теперь все грузики и обратимся к первоначальному механизму. Если бы Т₂было меньше Т₁, храповик вертелся бы вперед. Этому поверит любой. Но вот во что трудно поверить сразу, так это в обратное. Если T₂больше T₁, храповик вращает­ся назад! Динамический храповик с избытком теплоты внутри вертится назад, потому что собачка храповика отскакивает. Если собачка в какой-то момент находится на наклонной пло­скости, она толкает эту плоскость в сторону подъема. Но это происходит все время, ведь если случится, что собачка подни­мется достаточно высоко, чтобы проскочить край зубца, она окажется на новой наклонной плоскости. Словом, горячие храповик с собачкой идеально приспособлены для вращения в сторону, обратную той, в какую им первоначально предназна­чено было вертеться!

Как бы хитроумно мы ни сконструировали «однобокий» ме­ханизм, при равенстве температур он не захочет вертеться в одну сторону чаще, чем в другую. Когда мы смотрим на него, он может поворачиваться либо туда, либо сюда, но при продол­жительной работе ему никуда не уйти. Тот факт, что он не уйдет никуда, на самом деле фундаментальный, глубокий принцип; все в термодинамике покоится на нем.

§ 3. Обратимость в механике

Что же это за глубокий механический принцип, который утверждает, что при постоянстве температуры и достаточно про­должительной работе наше устройство не уйдет ни назад, ни вперед? Очевидно, мы получили фундаментальное утверждение о том, что нельзя придумать машину, которая, будучи пре­доставлена самой себе в течение долгого времени, охотней по­вернулась бы в какую-то одну определенную сторону. Попро­буем выяснить, как это вытекает из законов механики.

Законы механики действуют примерно так: сила есть масса на ускорение; сила, действующая на частицу, есть сложная функция положений всех прочих частиц. Бывает, что силы за­висят и от скорости, например в магнетизме, но не о них сейчас речь. Возьмем простой случай, скажем тяготение, когда силы определяются только расположением частиц. Положим, что мы решили нашу систему уравнений и получили для каждой части­цы определенную траекторию x(t). Для достаточно сложных систем и решения очень сложны; с течением времени возможно появление самых невероятных конфигураций. Если мы приду­маем любое, какое только нам придет в голову, расположение частиц и терпеливо подождем, то это расположение непременно наступит! Следя за решением в течение долгого времени, мы увидим, что оно как бы перепробует все, что возможно. В про­стейших устройствах это не обязательно, но в более или менее сложных системах с большим числом атомов такая вещь про­исходит.

Но решения способны и на большее. Решая уравнения дви­жения, мы можем получить некоторую функцию, скажем t+t²+t³. Мы утверждаем, что другим решением будет - t+t²-t³. Иными словами, если всюду в решение подставить -t вместо t, то мы получим еще одно решение того же уравнения. Это произойдет оттого, что при замене t на -t в первоначальном дифференциальном уравнении ничего не изменится: в нем при­сутствуют лишь вторые производные по времени. Значит, если наблюдается некоторое движение, то возможно и точно проти­воположное движение. К нашему замешательству, может ока­заться, когда мы следим за движением достаточно долго, что оно временами совершается в одну сторону, а временами — в обрат­ную. Одно направление ничем не привлекательней другого. Поэтому невозможно сконструировать машину, для которой после длительной работы одно направление окажется более вероятным, чем другое, если только машина достаточно сложна.

Можно, правда, изобрести машину, для которой это утверж­дение явным образом неверно. Взять, например, колесо, закру­тить его в пустом пространстве, и оно навсегда пойдет вертеться в одну сторону. Имеются поэтому некоторые условия, вроде сохранения момента вращения, из-за которых наши рассужде­ния нарушаются. Но это только означает, что наши доказатель­ства надо проделать поаккуратней. Надо, например, учесть, что вращательный момент забирают себе стенки или еще что-то, так что специальные законы сохранения перестают действовать. Тогда опять, если система достаточно сложна, наше доказатель­ство годится. Оно основано на обратимости законов механики.

Отдавая должное истории, мы хотели бы отметить устрой­ство, изобретенное Максвеллом, впервые разработавшим дина­мическую теорию газов. Он нарисовал такую картину: пусть имеются два сосуда с газом при одной и той же температуре. Между сосудами имеется маленькое отверстие. Возле него сидит небольшой чертик (конечно, это может быть и прибор!). В от­верстии есть дверца, чертик может ее открывать и закрывать. Он следит за молекулами, подлетающими слева. Как только он замечает быструю молекулу, он отворяет дверцу. Увидит мед­ленную — и дверцу на замок! Можно сделать его чертиком высшей квалификации, пристроив на затылок ему еще пару глаз, чтобы с молекулами в другом сосуде он поступал наобо­рот: пропускал налево медленные, а быстрые не выпускал. Вскоре левый сосуд остынет, а правый нагреется. Спраши­вается, будут ли нарушены идеи термодинамики существова­нием этакого чертика?

Оказывается, что если чертик конечного размера, то сам он вскоре так нагреется, что ничего не увидит. Простейшим чертиком явится, скажем, откидная дверца с пружинкой. Бы­строй молекуле хватает сил открыть дверцу и проскочить, а медленной не хватит, и она отлетит прочь. Но это опять-таки знакомая нам система храповик — собачка, только в другом виде; в конце концов механизм просто нагреется. Чертик не может не нагреться, если его теплоемкость не бесконечна. В нем, во всяком случае, имеется конечное число шестеренок и коле­сиков, так что он не сможет отделаться от излишка тепла, кото­рое приобретет, наблюдая молекулы. Вскоре он так начнет дрожать от броуновского движения, что не сможет сказать, что это там за молекулы, приближаются ли они, удаляются ли, словом, не сможет работать.

§ 4. Необратимость

Все ли законы физики обратимы? Конечно, нет! Попробуйте-ка, например, из яичницы слепить обратно яйцо! Или пустите фильм в обратную сторону — публика в зале тотчас же начнет смеяться. Необратимость — самая яркая черта всех событий.

Откуда же она появляется? Ведь ее нет в законах Ньютона. Если мы считаем, что любое явление может быть в конечном счете объяснено законами физики, и если также оказывается, что все уравнения обладают фантастическим свойством давать при t®-t другое решение, то ведь тогда обратимо любое явление. Но как же тогда получается, что в природе, в явлениях большого масштаба, все необратимо? Видимо, значит, есть какие-то законы, какие-то неизвестные нам, но важные уравне­ния, быть может, в электричестве, а может, в нейтринной фи­зике, для которых уже существенно, куда идет время.

Рассмотрим теперь этот вопрос. Один закон такого рода мы уже знаем — он утверждает, что энтропия только растет. Когда одно тело теплое, а другое холодное, тепло переходит от теплого к холодному. Это утверждение нам подошло бы. Но хорошо бы и этот закон понять с точки зрения механики. Нам уже удалось получить при помощи чисто механических соображений все следствия из постулата о том, что тепло не может течь в обрат­ную сторону; это помогло нам понять второй закон. Значит, не­обратимость из обратимых уравнений получать мы способны. Но использовали ли мы при этом только законы механики? Раз­беремся в этом глубже.

Так как речь зашла об энтропии, то нам придется найти ее микроскопическое описание. Когда мы говорим, что в чем-то (например, в газе) содержится определенное количество энер­гии, то мы можем обратиться к микроскопической картине этого явления и сказать, что каждый атом имеет определенную энергию. Полная энергия есть сумма энергий атомов. Равным образом, у каждого атома есть своя определенная энтропия. Суммируя, получим полную энтропию. На самом деле здесь все обстоит не так уж гладко, но все же давайте посмотрим, что получится.

В виде примера подсчитаем разницу энтропии газа при одной температуре, но в разных объемах. В гл. 44 для изменения энт­ропии мы получили

DS=?dQ/T.

В нашем случае энергия газа до и после расширения одна и та же, потому что температура не менялась. Значит, чтобы вос­полнить работу, проделанную газом, нужно придать ему какое-то количество тепла. Для малых изменений объема

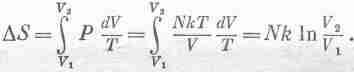
dQ=PdV. Подставив это в dQ, получим, как в гл. 44,

Например, при удвоении объема энтропия меняется на Nkln2.

Рассмотрим теперь другой интересный пример. Пусть име­ется цилиндр с перегородкой посредине. По одну ее сторону — неон («черные» молекулы), а по другую — аргон («белые» мо­лекулы). Уберем перегородку и позволим газам перемешаться. Как изменится энтропия? Можно представить себе, что вместо перегородки между газами стоит поршень с отверстиями, в ко­торые проходят белые молекулы и не проходят черные, и дру­гой поршень с обратными свойствами. Сдвигая поршень к осно­ванию цилиндра, легко понять, что для каждого газа задача сводится к только что решенной. Энтропия, таким образом, меняется на Nkln2; это значит, что энтропия на одну молекулу возрастает на kln2. Цифра 2 появилась оттого, что вдвое уве­личился объем, приходящийся на одну молекулу. Странное об­стоятельство! В нем проявилось свойство не самой молекулы, а свободного места вокруг нее. Выходит, что энтропия увели­чивается, когда температура и энергия не меняются, а измени­лось только распределение молекул!

Мы знаем, что стоит убрать перегородку, и газы через неко­торое время перемешаются из-за столкновений, колебаний, уда­ров молекул и т. д. Стоит убрать перегородку, и какая-то белая молекула начнет приближаться к черной, а черная — к белой, они проскочат мимо друг друга и т. д. Постепенно какие-то из белых молекул проникнут случайно в объем, занятый чер­ными, а черные — в область белых. Через какое-то время полу­чится смесь. В общем это необратимый процесс реального мира, он должен привести к росту энтропии.

Перед нами простой пример необратимого процесса, пол­ностью состоящего из обратимых событий. Каждый раз, когда происходит столкновение двух молекул, они разлетаются в оп­ределенных направлениях. Если запустить киноленту, на кото­рой засняты столкновения, в обратную сторону, то ничего непра­вильного на экране не появится. Ведь один вид столкновений столь же вероятен, как и другой. Поэтому перемешивание пол­ностью обратимо, и тем не менее оно необратимо. Каждому известно, что, взяв отдельно белое и отдельно черное и перемешав их, мы через несколько минут получим смесь. Подождем еще сколько-то там минут — они не отделятся, смесь останется смесью. Значит, бывает необратимость, основанная на обрати­мых ситуациях. Но теперь нам ясна и причина. Мы начали с расположения, которое в каком-то смысле упорядочено. В хаосе столкновений оно стало неупорядоченным. Переход от упоря­доченного расположения к беспорядочному является источником необратимости.

Конечно, если бы мы сняли на киноленту это движение и пустили бы потом пленку назад, то увидели бы, как постепенно устанавливается порядок. Кто-нибудь мог бы возразить: «Но это — против всех законов физики!» Тогда мы бы прокрутили фильм еще раз и просмотрели бы каждое столкновение. Все они были бы безупречны, каждое подчинялось бы законам фи­зики. Все дело, конечно, в том, что скорости каждой молекулы были бы выдержаны в точности, так что, если проследить их пути вспять, мы возвратимся к начальным условиям. Но такая ситуация крайне маловероятна. Если иметь дело не со специаль­но приготовленным газом, а просто с белыми и черными моле­кулами, их никогда не удалось бы вернуть назад.

§ 5. Порядок и энтропия

Итак, мы должны теперь потолковать о том, что понимать под беспорядком и что — под порядком. Дело не в том, что по­рядок приятен, а беспорядок неприятен. Наши смешанные и несмешанные газы отличаются следующим. Пусть мы разделили пространство на маленькие элементы объема. Сколькими спо­собами можно разместить белые и черные молекулы в элементах объема так, чтобы белые оказались на одной стороне, а черные на противоположной? И сколькими способами можно их разме­стить без этого ограничения? Ясно, во втором случае способов гораздо больше. Мы измеряем «беспорядок» в чем-то по числу способов, каким может быть переставлено его содержимое, лишь бы внешне все выглядело без изменения. Логарифм числа способов — это энтропия. В цилиндре с разделенными газами число способов меньше и энтропия меньше, т. е. меньше «бес­порядок».

Пользуясь этим техническим определением «беспорядка», можно понять наше утверждение. Во-первых, энтропия изме­ряет «беспорядок». Во-вторых, Вселенная всегда переходит от «порядка» к «беспорядку», поэтому энтропия всегда растет. Порядок не есть порядок в том смысле, что именно эта расста­новка молекул нам нравится; смысл в том, что число разных способов расставить молекулы (лишь бы со стороны расстановки выглядели одинаково) относительно ограничено. Когда мы кру­тили назад наш фильм о перемешивании газов, было не так уж много беспорядка. Каждый отдельный атом имел в точности необходимые скорость и направление, чтобы выйти куда поло­жено! Энтропия была в общем невысока, хотя это и не было за­метно.

А что можно сказать о необратимости других физических законов? Когда мы рассматривали электрическое поле ускоряе­мого заряда, было сказано, что мы должны брать запаздывающее поле. В момент t на расстоянии rот заряда надо брать поле, созданное ускорением в момент t-r/c, а не в момент t+r/c. Поэтому законы электричества на первый взгляд необратимы. Вместе с тем очень странно, что эти законы следуют из уравне­ний Максвелла, которые в действительности обратимы. Однако можно привести довод, что если бы мы пользовались только опережающим полем, полем, отвечающим положению дел в мо­мент t+r/c, и сделали это совершенно последовательно в пол­ностью замкнутом пространстве, то все происходило бы в точ­ности так же, как при употреблении запаздывающих полей! Эта кажущаяся необратимость в теории электричества, та­ким образом (по крайней мере в замкнутой полости), вовсе не является необратимостью. Вы это должны уже слегка сами чув­ствовать; вы знаете уже, что когда колеблющийся заряд создает поле, отражающееся от стен оболочки, то в конечном счете устанавливается равновесие, в котором односторонности нет места. Запаздывающие поля — только прием, удобный метод решения.

Насколько нам известно, все основные законы физики, по­добно уравнениям Ньютона, обратимы. Тогда откуда необра­тимость? Она — из-за превращения порядка в беспорядок. Но это утверждение все равно не понятно, пока мы не знаем, откуда порядок. Почему ситуации, в которых мы оказываемся ежеднев­но, никогда не бывают равновесными? Одно мыслимое объяс­нение таково. Рассмотрим снова наш цилиндр со смесью белых и черных молекул. Если следить за ним достаточно долго, может оказаться, что по чисто случайному, крайне невероятному, но все же мыслимому стечению обстоятельств белые молекулы рас­пределятся главным образом у дна, а черные — у крышки. После этого с течением времени они опять начнут перемеши­ваться.

Стало быть, одно возможное объяснение высокой степени упорядоченности нынешнего мира заключается в том, что нам просто повезло. Вероятно, как-то однажды во Вселенной слу­чилась флуктуация, все как-то разделилось, а теперь вновь воз­вращается к прежнему. Такая теория не несимметрична; на вопрос, как мог бы выглядеть разделенный газ немного раньше или немного позже, она ответит: в любом случае мы увидели бы серое пятно, потому что молекулы опять смешались бы. Как бы ни потекло время, вперед или назад, газ все равно переме­шался бы. Таким образом, по этой теории именно необратимость является одной из случайностей жизни.

Легко показать, что это не так. Предположим, что мы смот­рим не на весь цилиндр сразу, а на какую-то часть его. Пусть в какой-то момент мы открыли в этой части определенную сте­пень порядка: белое с черным в ней разделены. Что отсюда сле­дует для частей, которые мы еще не рассматривали? Если мы и впрямь считаем, что порядок возникает из беспорядка путем флуктуации, то мы обязаны рассмотреть самую вероятную флук­туацию из тех, которые способны в нашей части установить порядок. Но при такой наивероятнейшей флуктуации остальная часть сосуда вовсе не должна рассортироваться — совсем нао­борот! Значит, из гипотезы, что мир — это флуктуация, сле­дует, что, когда мы взглянем на часть мира, прежде нами не виденную, мы должны обнаружить в ней смесь, беспорядок, в отличие от известного нам прежде мира. Если весь наш поря­док есть флуктуация, выброс, мы не смеем надеяться на поря­док где-либо сверх того, где он уже обнаружен.

Теперь предположим, что разделение произошло от того, что в прошлом Вселенная была действительно упорядочена (не из-за флуктуации, а просто белое и черное были первоначально обособлены). Тогда эта теория предскажет, что в других местах тоже должен быть порядок, порядок не как случайность, а из-за того, что в прежние времена порядок был лучше. Тогда можно ожидать, что мы обнаружим в местах, которые мы еще не ви­дели, порядок.

Астрономы, например, пока наблюдали не все звезды. Каж­дую ночь они наводят свои телескопы на новые звезды, и эти звезды ведут себя так же, как и старые. Из этого мы заключаем, что Вселенная — не флуктуация и что наш порядок — это память о тех временах, когда все только начиналось. Мы не говорим, что нам понятна логика этого. По каким-то причинам Вселенная когда-то имела очень малую для своего энергосодер­жания энтропию, и с той поры энтропия выросла. Это — путь по направлению в будущее. В этом начало всех необратимостей. Именно это порождает процессы роста и распада. Именно из-за этого мы вспоминаем не будущее, а прошлое, вспоминаем собы­тия, которые ближе к тому моменту в истории мира, когда поря­док был лучше нынешнего. Именно поэтому мы не способны вспомнить события того времени, беспорядок при котором сильней теперешнего,— мы называем это время будущим.

Мы уже говорили когда-то, что в стакане вина откроется нам вся Вселенная, стоит только заглянуть в него поглубже. Ста­кан вина — штука достаточно сложная, есть там и влага, и стекло, и свет, и еще многое другое.

Прелесть физики еще и в том, что даже такие простые и иде­ализированные вещи, как храповик с собачкой, действуют лишь оттого, что и они — часть Вселенной. Храповик с собачкой работают в одну сторону только потому, что они находятся в тесном контакте с остальной Вселенной. Если бы храповик с собачкой поместить в сосуд и изолировать на некоторое время, то колесико перестанет предпочитать одно направление враще­ния другому. Но по той же причине, по какой мы, открывая шторы, впускаем свет, из-за чего мы идем остывать в тень и греть­ся на солнце, по той же причине храповик с собачкой вертятся лишь в одну сторону. Односторонность связана как-то с тем, что храповик — это часть нашей Вселенной. Часть Вселенной не только в том смысле, что подчиняется законам Вселенной, но и потому, что его одностороннее поведение связано с односторон­ним поведением всей Вселенной. Оно не может пока быть понято до конца: наука приоткрыла великую тайну ранней истории мира, которая сейчас служит лишь предметом разных гипотез.