Законы эллиптического движения Кеплера

Законы эллиптического движения Кеплера

Вторым человеком, сыгравшим решающую роль в утверждении гелиоцентрической системы, был немецкий ученый Иоганн Кеплер (1571–1630), рис. 2.7. Иоганн родился в бедной семье. Поступил в Тюбингенский университет, где с увлечением занимался математикой и астрономией. Его учитель профессор Местлин втайне был последователем Коперника. Конечно, в университете Местлин преподавал астрономию по Птолемею, но дома он знакомил своего ученика с основами нового учения. И вскоре Кеплер стал горячим и убежденным сторонником теории Коперника. Он закончил обучение как священник, но не был допущен к богословской деятельности, как вольнодумец. Он стал профессором математики и морали в городе Граце.

Рис. 2.7. Иоганн Кеплер

Затем был вынужден переезжать с места на место, в основном, из-за преследований со стороны католической церкви. Жил и умер в нищете.

Несмотря на жизненные перипетии, Кеплер в любых условиях вел научную работу. Для Карла Маркса, как пример самоотверженности, он был одним из двух любимых героев, другим был Спартак. После смерти Кеплера наследникам досталось: поношенная одежда, 22 флорина наличными, 29 000 флоринов невыплаченного жалованья, 27 опубликованных рукописей и множество неопубликованных – они позже были изданы в 22-томном сборнике. Со смертью Кеплера его злоключения не закончились. В конце Тридцатилетней войны было полностью разрушено кладбище, где он похоронен, и от его могилы ничего не осталось. Часть архива Кеплера исчезла. В 1774 году большую часть архива (18 томов из 22) приобрела Петербургская академия наук, там всё и хранится в настоящий момент.

Альберт Эйнштейн назвал Кеплера «несравненным человеком» и писал о его судьбе: «Он жил в эпоху, когда еще не было уверенности в существовании некоторой общей закономерности для всех явлений природы. Какой глубокой была у него вера в такую закономерность, если, работая в одиночестве, никем не поддерживаемый и не понятый, он на протяжении многих десятков лет черпал в ней силы для трудного и кропотливого эмпирического исследования движения планет и математических законов этого движения!»

Основываясь на мистической натурфилософии и пантеистических мотивах, Кеплер развил мысль о мировой гармонии. В его ранних работах использовались пифагорейские идеи. Число планет и расстояния от них до Солнца были связаны с числом и расположением правильных геометрических (евклидовых) тел, при этом движение планет вокруг Солнца объяснял действием своеобразных интеллектуальных сил, или душ. Эти результаты сегодня не представляют особой ценности (их критиковали и современники, в частности, Галилей). Но их публикация в 1596 году в книге, которую коротко называют «Космографической тайной», привлекла внимание Тихо Браге. Он пригласил Кеплера к себе в Прагу для совместной работы. Именно это сотрудничество, которое состояло в кропотливом анализе точных данных каталогов наблюдений Тихо Браге за движениями планет, привело к замечательным результатам.

В 1600 году Кеплер занялся исследованием движения Марса. Он перебрал всевозможные комбинации эпициклов, деферентов, эксцентров и эквантов, чтобы добиться наилучшего совпадения расчетных результатов с наблюдаемым перемещением планеты, но добился точности в совпадении угловых координат планет лишь в 8 угловых минут, то есть всего около ? видимого диаметра лунного диска. Даже по тем временам это было очень низкой точностью. Естественно, такой результат не удовлетворил Кеплера. Часто приводят его слова: «эти 8 минут привели к пересмотру всей астрономии». Перебрав около семидесяти различных комбинаций, Кеплер пришел к выводу, что орбита Марса должна быть эллипсом.

Чтобы согласиться с собственным выводом, Кеплеру нужно было переломить себя. Как и большинство его современников, он был убежденным сторонником концепции идеального кругового движения. К сожалению, в 1601 году скончался Тихо Браге, но бесценные записи его наблюдений остались у Кеплера, и он в полной мере ими воспользовался.

Свои открытия Кеплер опубликовал в 1609 году в книге «Новая астрономия». В последующие годы он существенно дополнил свою работу, включив в нее даже результаты исследования движения спутников Юпитера; эти результаты были напечатаны в 1619 и 1621 годах. Из огромной массы полезных сведений и довольно-таки путаных рассуждений были выведены и сформулированы три закона движения планет. Первые два были даны в «Новой астрономии», третий – в труде «Гармония мира», изданном в 1619 году. Сегодня они известны под названием законов Кеплера. В современной формулировке эти законы звучат так:

Первый закон: Каждая планета движется по эллипсу, в одном из фокусов которого находится центр Солнца.

Второй закон: Площадь сектора орбиты, описанная радиус-вектором планеты, изменяется пропорционально времени.

Третий закон: Квадраты времен обращения планет вокруг Солнца относятся как кубы их средних расстояний от Солнца (под «средним расстоянием» здесь понимается большая полуось эллипса):

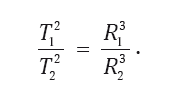
Законы Кеплера показали, как движутся планеты. Это, конечно, имеет практическую ценность для небесной механики. На рис. 2.8 проиллюстрирован второй закон Кеплера, где показано, что за равное время t радиус-вектор «Солнце – планета» «заметает» равные площади S. Очевидно, что чем ближе планета к Солнцу, тем больше ее скорость. Третий закон легко позволяет найти среднее расстояние планеты от Солнца, если известно время ее полного обращения по орбите. Эти вычисления принимают особо простой вид, если расстояние измерять в астрономических единицах (1 а. е. равна среднему расстоянию от Солнца до Земли), а время – в годах (время одного полного оборота Земли вокруг Солнца). Если период обращения планеты вокруг Солнца равен T годам, то ее среднее расстояние от Солнца в астрономических единицах равно T^2/3.

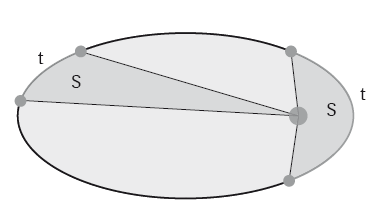
Рис. 2.8. Иллюстрация второго закона Кеплера

Выводы Кеплера – это результат многолетнего кропотливого труда, но они не сразу были восприняты сторонниками теории Коперника. Галилей, как говорилось, «до конца» оставался верен концепции круговых движений. Однако простота в расчетах при использовании законов Кеплера была неоспоримой, а точность предсказания положения планет значительно превосходила птолемеевские. Все это обеспечило законам Кеплера широкое признание и популярность в использовании уже в XVII веке.

Данный текст является ознакомительным фрагментом.