Скорость распространения гравитационных взаимодействий
Скорость распространения гравитационных взаимодействий
В конце главы обсудим еще одну интересную проблему. ОТО включает две фундаментальных константы: гравитационную G и скорость света c. Присутствие первой из них очевидно и естественно – мы имеем дело с гравитационной теорией. Но скорость света – это скорость электромагнитного взаимодействия. А электромагнитное и гравитационное взаимодействия совершенно разной природы. Строго говоря, в ОТО должна быть другая константа – скорость распространения гравитационного взаимодействия, обозначим ее cg. Фактически Эйнштейн постулировал использование скорости света. Возможно, основанием для этого был принцип соответствия с СТО, где фигурирует как раз скорость света. Но это не выглядит убедительно. Если нет серьезных теоретических оснований, то этот факт нужно проверять. Этой проблемой занялся больше 10-ти лет назад научный тандем в составе нашего соотечественника (сейчас работающего в США, в университете Миссури-Коламбия), теоретика Сергея Копейкина и американского экспериментатора Эдварда Фомалонта из Национальной Астрономической Обсерватории, Шарлотсвилл, США. Мы коротко приведем их постановку задачи и результаты.
Представим, что Солнце внезапно исчезло из центра нашей Солнечной системы. Через какое время Земля почувствует его исчезновение? Для света все ясно: поскольку известна его скорость распространения, то оптически исчезновение Солнца обнаружится только через 8 мин 20 сек. Это время необходимо свету, чтобы преодолеть расстояние в одну астрономическую единицу (150 млн км), отделяющее нас от Солнца.
ОТО предсказывает точно такое же время и для исчезновения гравитационного притяжения Солнца на орбите Земли. В этом случае Земля продолжит движение по своей орбите в течение еще 8 мин 20 сек, а затем начнет двигаться по прямой линии, так как сигнал об исчезновении притяжения Солнца дойдет именно за это время. В отличие от ОТО, в теории Ньютона Земля мгновенно почувствует отсутствие Солнца. Но этим фантастическим способом невозможно экспериментально определить скорость распространения гравитационного взаимодействия.
Реальное явление – это некоторые гравитационные возмущения Солнца, связанные с его движениями относительно центра масс Солнечной системы. Однако центр Солнца расположен недалеко от центра масс всей Солнечной системы, и изменения гравитационного поля, вызываемые небольшими долговременными колебаниями положения Солнца относительно этой точки, пренебрежимо малы и недоступны для современных наблюдений. Скорость распространения гравитационного взаимодействия cg (скорость гравитации) можно измерить только в том случае, если гравитационное поле является переменным и эта переменность достаточно быстрая, чтобы возникли гравитационные релятивистские эффекты, доступные для современной измерительной техники. При этом возможны два метода, один из которых основан на детектировании гравитационных волн и прямом измерении скорости их распространения, а второй – на измерении переменного гравитационного поля движущегося тела. Как мы уже знаем, пока гравитационные волны не зарегистрированы непосредственно. А вот вторая возможность оказалась перспективной.
Изложим идею эксперимента Копейкина-Фомалонта. Самым массивным телом в Солнечной системе, которое создает переменное гравитационное поле, является Юпитер. Для данного эксперимента его движение можно вполне считать прямолинейным и равномерным. Как на примере этой модели можно представить, что гравитационное взаимодействие передается с конечной скоростью? Если бы использовалась теория Ньютона, где скорость передачи гравитационного взаимодействия бесконечна, то эквипотенциальные («равно-силовые») поверхности, перемещались бы, как вмороженные, вместе с Юпитером, оставляя его в центре. Но поскольку скорость распространения конечна, то эквипотенциальные поверхности будут запаздывать. Механизм запаздывания показан на рис. 10.6. Пусть за время ?t информация о положении Юпитера в точке А переместилась до поверхности А?. Но за это же время Юпитер перейдет из точки А в точку В, то есть сместится из центра этой поверхности, и т. д.
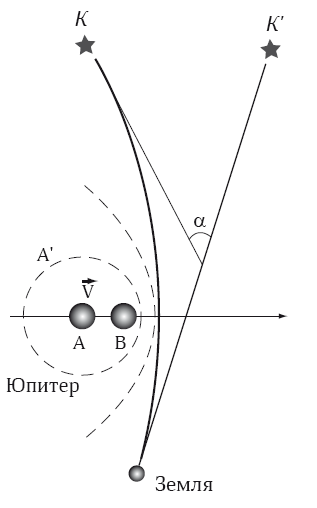
Рис. 10.6. Отклонение радиоволны в переменном поле Юпитера
Теперь ясно, что для оценки скорости гравитационного взаимодействия, нужно оценить степень запаздывания. А для этого необходимо «поэкспериментировать» с переменным гравитационным полем Юпитера, анализируя излучение, проходящее рядом с ним. В качестве источника излучения был выбран радиоквазар за Юпитером, радиоволны от которого детектировались на Земле. Наблюдалось положение на небе квазара К? во время прохождения Юпитера и сравнивалось с его же положением К на «чистом» небе. Таким образом определялся угол ? отклонения радиоволн переменным гравитационным полем Юпитера.
Теперь предположим, что фундаментальная скорость, которая входит в ОТО – это не c, а независимая скорость распространения гравитационного взаимодействия cg. Какая бы скорость не использовалась, ОТО позволяет рассчитать теоретически переменное гравитационное поле движущегося Юпитера. Электромагнитная волна (фотоны), испущенные квазаром, движутся по геодезическим этого поля. Для определения геодезической существенными являются производные от метрики, которые для переменного гравитационного поля Юпитера характеризуются отношением V/cg, где V – скорость Юпитера. При анализе отклонения радиоволн от квазара рассматривались эффекты, связанные как раз с этим отношением. В пределах точности данного эксперимента было установлено, что скорость распространения гравитационного взаимодействия численно равна скорости света в вакууме, cg = c.
Провести аналогичный эксперимент в поле Солнца невозможно, поскольку оно статично, и уравнение его движения не содержит членов типа V/cg. Вспомним также о гравитационных волнах. В эксперименте Копейкина-Фомалонта речь шла о фундаментальной скорости в ОТО, как скорости передачи гравитационного взаимодействия cg, как бы не связанной с распространением волн. Однако уравнения ОТО устроены так, что гравитационные волны будут распространяться с той же скоростью. После эксперимента можно утверждать, что в пределах точности измерений эта скорость равна c.
Данный текст является ознакомительным фрагментом.