7. История с почти детективным началом. Загадка века. Ионы и электроны. Невидимка находит напарника. Строем сквозь кристалл. Вопросы без ответа.
7. История с почти детективным началом. Загадка века. Ионы и электроны. Невидимка находит напарника. Строем сквозь кристалл. Вопросы без ответа.
Многие занимательные детективные истории начинаются с… исчезновения. Поиски пропажи, будь это человек, документ или драгоценный камень, служат основой остросюжетного повествования.
На этот раз речь идет о необычной пропаже. Как читатель уже знает, исчезло электрическое сопротивление.
Приступая к следствию по такому необыкновен — ному делу, мы должны прежде всего уяснить себе, что такое электрическое сопротивление вообще.
Напомним, что металл представляет собой сложную систему, состоящую из положительных ионов, то есть атомов, потерявших один или несколько электронов, и электронов, находящихся в свободном состоянии. Эти свободные электроны, или, как их называют, электроны проводимости, и являются носителями электрического тока.
В идеальном кристалле ионы расположены в строгом порядке, каждый на своем месте. Они находятся в узлах пространственной решетки, так называемой кристаллической решетки.
Для того чтобы представить себе размеры этого микромира, достаточно сказать, что для измерения расстояния между соседними ионами, самая маленькая мера длины, применяемая в технике, — микрометр, равная, как вытекает из ее названия, одной миллионной доли метра, оказалась слишком большой. Расстояние между ионами в кристаллической решетке измеряется в нанометрах (один нанометр равен одной миллиардной доли метра).
Напомним еще раз, что поведение «невидимок» (микрочастиц) подчиняется особым квантовым законам.
В идеальном кристалле электрон ведет себя как волна. Он свободно проходит сквозь кристаллическую решетку, подобно тому как световая волна распространяется в прозрачной среде.
Поэтому в идеальном кристалле сопротивление электрическому току отсутствует.
При температуре выше абсолютного куля ионы совершают тепловые колебания. Порядок в кристалле нарушается.
Такая среда перестает быть прозрачной для электронов. Происходит, как говорят физики, рассеивание электронов, подобно тому как морская волна рассеивается, встретив препятствие. Электроны рассеиваются также на атомах примесей, хаотично расположенных в кристалле.
Возникает сопротивление прохождению электрического тока, или, короче, электрическое сопротивление.
Но вот в 1950 году при исследовании сверхпроводимости ртути оказалось, что критическая температура образцов ртути зависит от их изотопного состава. Она возрастает при уменьшении среднего атомного веса исследуемого образца.
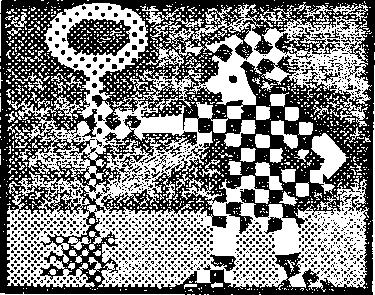
Это явление, обнаруженное впоследствии также на олове, галлие и некоторых других сверхпроводящих элементах, получило название изотопического эффекта.
Изотопический эффект — чудесный ключ, с помощью которого ученые получили воз можность открыть дверь в замечательный мир сверхпроводимости.
Известно, что масса ионов кристаллической решетки в тысячи раз больше массы свободных электронов.
Поэтому масса изотопа является характеристикой кристаллической решетки и главным образом влияет на ее свойства.
После открытия изотопического эффекта стало ясно, что сверхпроводимость, которая вообще является свойством системы электронов, каким?то образом связана с состоянием кристаллической решетки.
А значит, и возникновение эффекта сверхпроводимости обусловлено взаимодействием электронов с решеткой кристалла. Это взаимодействие ответственно за появление электрического сопротивления, а при определенных условиях оно должно привести к отсутствию электрического сопротивления, то есть к сверхпроводимости.
Прошло всего несколько лет после открытия изотопического эффекта, и в 1957 году американские исследователи Дж. Бардин, Л. Н. Купер и Дж. Р. Шриффер (этот триумвират принято сокращенно называть БКШ — по первым буквам их фамилий) и советский ученый Николай Николаевич Боголюбов создали теорию, объясняющую явления, происходящие в мире сверхпроводимости.
На «живом серебре» (такое образное название носит ртуть на украинском и немецком языках) была впервые открыта сверхпроводимость. Именно на ртути был обнаружен изотопический эффект, создавший важную предпосылку для разработки современной теории сверхпроводимости.
На страницах этой книги мы лишены возможности пользоваться сложными математическими уравнениями, описывающими законы квантовой механики. Поэтому дается лишь упрощенное представление о природе сверхпроводимости.
В обычном проводнике каждый электрон ведет себя как индивидуалист. Между электронами проводимости отсутствует, образно говоря, чувство локтя. Более того, по закону Кулона электрон отталкивает соседа.
В сверхпроводниках происходит объединение электронов в пары. Участники таких пар притягиваются друг к другу.
У читателя, твердо усвоившего из элементарного курса физики, что между электронами существуют кулоновские силы отталкивания, это последнее утверждение не может не вызвать недоумения.
Но возможность электронов при определенных услових притягиваться друг к другу не противоречит законам физики.
Свободный электрон, двигаясь через кристаллическую решетку, притягивает к себе положительные ионы металла, вызывая тем самым деформацию решетки. Это приводит к появлению в решетке области избыточного положительного заряда, образующейся благодаря высокой плотности ионов там, где решетка деформировалась.
Второй электрон притягивается избытком положительного заряда и тем самым косвенно взаимодействует с первым электроном (то есть притягивается к нему).
При достаточно низких температурах у ряда металлов такое притяжение преобладает над кулоновским отталкиванием. Тогда электроны могут объединяться попарно.
Такие пары электронов получили название куперовских пар, по имени Л. Купера, одного из создателей теории сверхпроводимости.
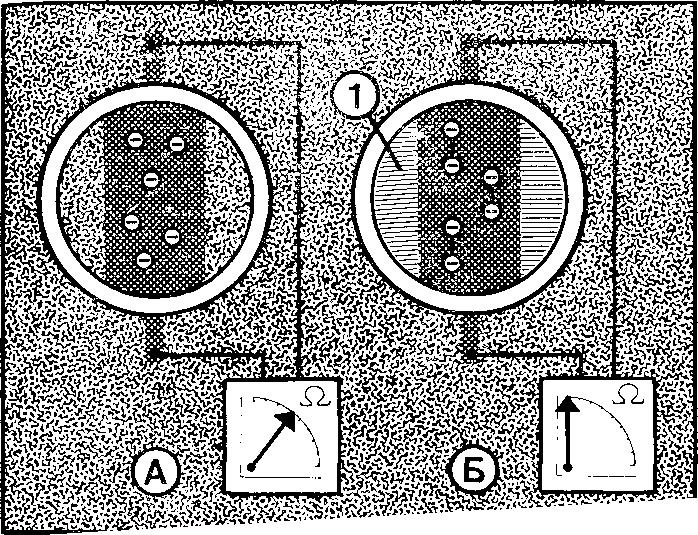
Невидимка находит напарника. I — жидкий гелий. А — в обычном проводнике электроны перемещаются в одиночку, каждый из них отталкивает соседа. Б — в сверхпроводнике электроны объединяются в пары. Строй куперовских пар свободно перемещается по кристаллу. Электрическое сопротивление равно нулю.
Казалось, электрону легче всего выбрать себе напарника из ближайших соседей. Но это не так. Напарник электрона должен находиться от него на относительно большом расстоянии, с тем чтобы ку- лоновская сила отталкивания была достаточно мала.
Электроны куперовской пары находятся друг от друга на расстоянии один микрометр. В обыденной жизни это, разумеется, мизерная величина. Но не забывайте, что мы с вами сейчас находимся в микромире, где счет идет на доли нанометра.
Электрон должен «чувствовать» своего напарника, находящегося от него на расстоянии, в десятки тысяч раз превышающем расстояние до его ближайшего соседа.
Если мы мысленно построим шар радиусом в один микрометр, в центре которого один из электронов куперовской пары, то его партнер должен находиться где?то на поверхности шара. Между тем внутри этого шара находятся мириады электронов.
Каким?то удивительным для нас, жителей макромира, способом электрон в таких условиях выбирает себе напарника. И не ошибается в своем выборе! Расчеты показывают, что образование сформированных таким образом куперозских пар энергетически наиболее выгодно.
Спаривание двух электронов возникает только тогда, когда большое число других электронов находится в этом же состоянии.
Такой коллектив электронов в кристалле можно уподобить строю солдат, совершающих марш по местности, пересеченной завалами и рытвинами. Здесь каждый подстраховывает своего товарища, не давая ему оступиться или попасть в яму.
Точно так же «строй» куперовских пар легко «марширует» по сверхпроводнику. Электрическое сопротивление исчезает.
Однако с ростом температуры интенсивность тепловых колебаний увеличивается, и при температуре выше критической куперовские пары распадаются. Сверхпроводник превращается в обычный проводник.
В сверхпроводнике, при температуре отличной от абсолютного нуля, не все электроны объединяются в куперовские пары. Наряду со спаренными электронами там имеются и обычные электроны, которые могут рассеиваться и испытывать сопротивление так же, как электроны проводимости в нормальном кристалле.
Количество куперовских пар уменьшается при повышении температуры и приближении ее к критической. Наоборот, при абсолютном нуле все электроны должны образовать пары.
Из рассказанного в предыдущей главе читатель уже знает, что электроны проводимости в металле ведут себя как Ферми — жидкость.
Электронная жидкость движется под действием электрического поля в кристаллической решетке, как обычная жидкость по трубопроводу под действием перепада давления. Взаимодействуя с кристаллической решеткой и всевозможными примесями, электроны рассеиваются, испытывая сопротивление движению.
«Трение» электронной жидкости о кристалл, то есть ее «вязкость», мы наблюдаем как сопротивление электрическому току.
Исчезновение сопротивления в сверхпроводнике можно трактовать как исчезновение вязкости элек тронной жидкости. Таким образом, сверхпроводимость можно рассматривать как сверхтекучесть электронной жидкости. Сверхпроводимость, как мы уже знаем, осуществляется благодаря спариванию электронов. Иными словами, в момент перехода в сверхпроводящее состояние Ферми — жидкость переходит в Бозе — жидкость.
Так как при переходе в сверхпроводящее состояние не все электроны спариваются, мы можем представить себе сверхпроводник как бы пропитанным двумя электронными жидкостями. Одна из них, состоящая из нормальных электронов, обладает свойством обычной жидкости, другая, состоящая из куперовских пар, — сверхтекуча.
В сверхпроводнике ток может переноситься как нормальными, так и спаренными электронами.
Постоянный ток весь переносится куперовскими парами. В этом случае сверхпроводящий металл подобен двум параллельным проводникам: один из которых с нормальным сопротивлением, другой с сопротивлением равным нулю; причем проводник с нулевым сопротивлением шунтирует проводник с нормальным сопротивлением, а следовательно, общее сопротивление равно нулю.
Если ток переменный, то часть тока в сверхпроводнике может переноситься нормальными электронами. Однако при относительно небольших частотах эта часть невелика.
Читателя, наверное, интересует судьба и другой Ферми — жидкости — гелия 3.
После того как стал ясным механизм спаривания электронов в металле, напрашивалась мысль, что похожий процесс может произойти и в гелии 3.
Расчеты показали, что при достаточно сильном охлаждении здесь неминуемо должны спариваться атомы гелия.
Штурм абсолютного нуля продолжался.
Наконец в 1972 году при температуре 0,00265К гелий 3 был получен в сверхпроводящем состоянии.
Завершая рассказ о гелии 3, уместно остановиться еще на одном интересном свойстве этой квантовой жидкости.
Оказывается, гелий 3 сохраняет конечную растворимость (около 6 %) в жидком гелии 4 вплоть до абсолютного нуля температуры.
Возникла идея использовать это свойство для того, чтобы заставить гелий 3 и гелий 4 «работать» совместно.
Действительно, при соприкосновении почти чистого жидкого гелия 3 с разбавленным раствором гелия 3 в гелии 4 атомы гелия 3 должны перейти в раствор. При этом поглощается теплота растворения, и температура раствора понижается.
Растворение осуществляется в одной части прибора — в камере растворения, а удаление атомов гелия 3 из раствора путем откачки в камере испарения.
Непрерывная циркуляция гелия 3 осуществляется системой насосов и теплообменников. При этом в камере растворения можно неограниченно долго поддерживать температуру 10–20 милликельвинов.
Другими способами можно достигнуть и еще более низких температур — в миллиардные доли кельвина.
Современная теория сверхпроводимости позволяет объяснить ряд явлений, долгое время считавшихся загадочными.
Стало ясным, например, почему различные аллотропические модификации одного и того же металла, отличающиеся друг от друга различной структурой кристаллической решетки, имеют разные критические температуры перехода в сверхпроводящее состояние.
Кристаллическая решетка, как читатель уже знает, играет важную роль в процессе сверхпроводимости.
Для того чтобы понять суть другого удивительного явления — квантования магнитного потока в сверхпроводящем контуре, — уместно привести следующую аналогию.
В 1911 году Резерфорд предложил планетарную модель атома, согласно которой в центре атома находится положительно заряженное ядро, вокруг которого движутся электроны, подобно планетам вокруг Солнца. Движущиеся с центростремительным ускорением электроны должны непрерывно излучать электромагнитную энергию. В соответствии с законами классической физики они должны были потерять всю свою энергию и упасть на ядро. Между тем давно известно, что атом представляет собой устойчивую систему частиц.
Разрешить это противоречие удалось в 1913 году датскому физику Нильсу Бору, заложившему основы современной квантовой теории атома.
Согласно постулатам Бора, энергия электрона в атоме и ряд других величин не могут изменяться непрерывно. Допустимы только определенные значения физических величин, а следовательно, только определенные орбиты. Двигаясь вокруг ядра по своим «разрешенным» орбитам, электроны не излучают электромагнитные волны.
Представьте себе сверхпроводящее кольцо, по которому течет ток. Электроны в сверхпроводящем кольце как бы движутся по гигантским боровским орбитам. Поэтому к их движению применимы правила квантования Бора.
Сверхпроводящий ток создает вне сверхпроводника магнитное поле, а следовательно, и магнитный поток (вспомните, так называют произведение индукции магнитного поля на величину площади, охватываемой контуром). Оказывается, что эта величина может принимать только дискретный (прерывистый) ряд значений. Иными словами, магнитный поток квантуется.
Если при изучении свойств атома мы сталкиваемся с квантованием в микромире, которое мы не в состоянии непосредственно наблюдать, то сверхпроводимость дает нам пример квантования макроскопической величины — потока магнитного поля.
Здесь мы наблюдаем квантовый эффект, гигантский по своим масштабам.
Теоретически и экспериментально установлено, что величина минимальной порции — кванта магнитного потока — составляет две десятимиллионные доли гаусса[6] на квадратный сантиметр.
Эффект квантования магнитного потока послужил прекрасной основой для создания приборов, измеряющих электрические и магнитные величины с немыслимой ранее точностью.
Может ли современная теория сверхпроводимости дать исчерпывающее объяснение всех явлений, происходящих в этом удивительном мире?
Исследователи пока не могут теоретически рассчитать критическую температуру конкретных металлов и с полной достоверностью ответить на вопрос, способен ли тот или иной металл стать сверхпроводником. Осталось немало и других нерешенных проблем.
Напомним читателю, что явление сверхпроводимости впервые наблюдалось в 1911 году. Но только в 1957 году, спустя почти полвека, наука смогла дать ответ на вопрос, что такое сверхпроводимость.
В науке случается так, что теория отстает от экспериментальных исследований. Но другой пример такого большого отставания привести трудно. Это свидетельствует о сложности и необычности проблемы сверхпроводимости.
Наука не существует изолированно от материальной жизни общества. Наиболее интенсивно проводятся научные исследования, которые обещают практический выход.
Начало второй половины XX века ознаменовалось рядом открытий в области сверхпроводимости, завершившихся разработкой теории сверхпроводимости.
В 1957 году была опубликована работа молодого советского физика Алексея Алексеевича Абрикосова, в которой впервые изложена теория сверхпроводимости сплавов.