Глава пятая ЧАСЫ И ЛИНЕЙКИ КАПРИЗНИЧАЮТ

Глава пятая

ЧАСЫ И ЛИНЕЙКИ КАПРИЗНИЧАЮТ

Снова садимся в поезд

Перед нами очень длинная железная дорога, по которой движется поезд Эйнштейна. На расстоянии 864 000 000 километров друг от друга находятся две станции. При скорости 240 000 километров в секунду поезду Эйнштейна понадобится час, чтобы пройти это расстояние.

На обеих станциях имеются часы. На первой станции в вагон садится путешественник и перед отходом поезда проверяет свои часы по станционным. По приезде на другую станцию он с удивлением замечает, что его часы отстали. В мастерской путешественника заверили, что его часы в полном порядке.

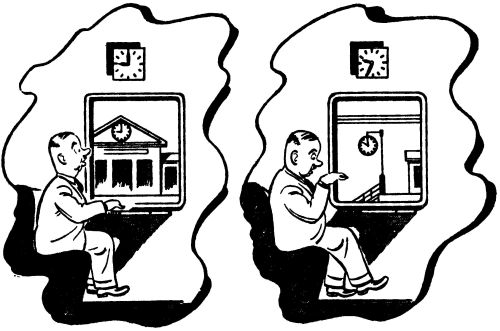
В чем же дело?

Чтобы разобраться в этом, представим, что пассажир направляет к потолку луч света из фонарика, поставленного на пол вагона. На потолке расположено зеркало, от которого луч света отражается обратно к лампочке фонарика. Путь луча, каким его видит пассажир в вагоне, изображен в верхней части рисунка на стр. 51. Совсем иначе выглядит этот путь для наблюдателя, находящегося на платформе. За то время, что луч света пройдет от лампочки до зеркала, само зеркало вследствие движения поезда переместится. Пока луч будет возвращаться, лампочка переместится еще на такое же расстояние.

Мы видим, что для наблюдателей на платформе свет прошел явно большее расстояние, чем для наблюдателей в поезде. С другой стороны, мы знаем, что скорость света есть абсолютная скорость, она одинакова и для едущих в поезде, и для тех, кто стоит на платформе. Это заставляет нас сделать вывод: на станции между отправлением и возвращением луча света прошло больше времени, чем в поезде!

Нетрудно вычислить отношение времен.

Предположим, наблюдатель на платформе установил, что между отправлением и возвращением луча света прошло 10 секунд. За эти 10 секунд свет пробежал 300 000 X 10 = 3 000 000 километров. Отсюда следует, что стороны АВ и ВС равнобедренного треугольника ABC составляют каждая 1 500 000 километров. Сторона АС равна, очевидно, пути, пройденному поездом за 10 секунд, то есть 240 000 X 10 = 2 400 000 километров.

Теперь легко определить высоту вагона, которая будет высотой BD треугольника ABC.

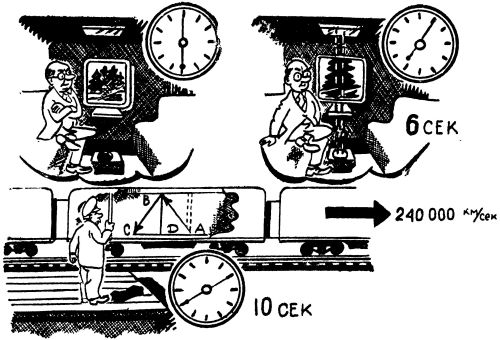
В прямоугольном треугольнике квадрат гипотенузы (АВ) равен сумме квадратов катетов (AD и BD). Из равенства: AB² = AD² + BD² получаем, что высота вагона 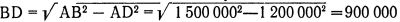километров. Высота весьма солидная, что, впрочем, не удивительно при астрономических размерах поезда Эйнштейна.

Путь, пройденный лучом от пола до потолка вагона и обратно, с точки зрения пассажира, равен, очевидно, удвоенной высоте, то есть 2 X 900 000 = 1 800 000 километров. Для прохождения этого пути свету понадобится 1 800 000 / 300 000 = 6 секунд.