1.3.4. Математическая модель радиоактивного распада. Эмпирический закон и его статистическое обоснование

В 1902 г. в журнале Philosophical Magazine вышла статья Эрнеста Резерфорда и Фредерика Содди, озаглавленная «Причина и природа радиоактивности». В этой статье впервые радиоактивный распад был описан математически.

Эти авторы изучали распад так называемого ThX (В то время еще не была сформулирована изотопная концепция и исследователи относились к этой радиоактивной субстанции как к индивидуальному веществу, хотя указывали, что «сейчас еще мало что известно о действительной природе активного компонента тория». Позже было установлено, что это радиоизотоп ²²⁴Ra с периодом полураспада 3,64 сут.) и заметили, что «активность ThX уменьшается со временем приблизительно в геометрической прогрессии, т.е. если через I_o обозначить начальную активность, а через I_t – активность спустя время t, то

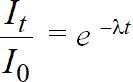, (1.1)

где ? – постоянная; e – основание натуральных логарифмов».

Вслед за Резерфордом и Содди будем пока называть величину I_t “активностью” (добавляя от себя – в смысле, принятом Резерфордом) или “инструментальной активностью”. Поскольку в эмпирической формуле (1.1) взято отношение значений этой «активности» в разные моменты времени, то размерность величины I_t для проверки выполнимости (1.1) безразлична, т.е. задача сводится к измерению относительной убыли I_t со временем.

В дальнейшем для простоты будем опускать индекс «t» у символа I и всех других символов величин, зависящих от времени и пропорциональных I.

В настоящее время считается твердо установленным, что излучение, производимое радионуклидами, есть следствие ядерных превращений (Интересная подробность: закон радиоактивных превращений сформулирован в 1902 г., а планетарная модель атома, предполагающая существование атомного ядра, предложена Резерфордом позже, – в 1911 г. Таким образом, Резерфорд, выявив экспоненциальный закон убывания способности радиоактивного препарата излучать, еще и сам не мог связывать это явление с «ядерными превращениями». В дальнейшем оба понятия – «радиоактивный распад» и «ядерные превращения» будут в равной мере использоваться как равнозначные). Это знание позволяет утверждать, что, чем выше скорость ядерных превращений, тем интенсивнее излучение и тем больше значение той величины, которая выше была названа «активностью» (в смысле, принятом Резерфордом). Иными словами, вполне допустимо измерять не интенсивность общего излучения, производимого образцом радионуклида, т.е. измерять не поток, а только некоторую (но всегда одну и ту же) часть ионизационного эффекта, которая регистрируется инструментально, чтобы наблюдать экспоненциальное убывание радиоактивности как некий феномен, допускающий количественную оценку.

Итак, рассуждая на современном уровне достигнутых знаний, можно утверждать, что инструментальная активность (или активность в смысле Резерфорда) пропорциональна скорости ядерных превращений:

I – – dN/dt, (1.2)

где N – число ядер радионуклида как функция времени (для очень больших значений N эту функцию допустимо полагать непрерывной); – – символ прямой пропорциональности; знак «минус» перед производной («мгновенной» скоростью, т.е. «приростом числа ядер в единицу времени») поставлен для того, чтобы компенсировать отрицательное значение этого обобщенного «прироста», который в действительности является убылью.

Опытным путем, трудами многих исследователей было установлено, что при измерении излучения одного и того же препарата с помощью одного и того же инструментального метода величина I не зависит ни от каких внешних факторов (температура, давление, освещенность, электрические и магнитные поля; природа и структура химического соединения, в состав которого входит радионуклид* и др. Слабая зависимость параметра ? от внешних условий выявлена только для K-захвата.), а зависит только от времени; но при измерении массы радионуклида I пропорционально изменяет свое значение (т.е. является экстенсивной величиной).

Таким образом,

I – m, (1.3)

где m – масса радионуклида.

Но из признания истинности атомно-молекулярной концепции строения вещества (на чем строится все современное естествознание) следует, что

m – N . (1.4)

Из сопоставления пропорциональных связей (1.2)-(1.4) следует, что

– dN/dt – N.

Введя коэффициент пропорциональности k, получаем дифференциальное уравнение с разделяющимися переменными

– dN/dt = kN, (1.5)

интегрирование которого при условии: t = 0, N = N₀

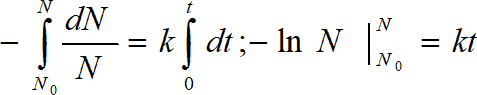
приводит к выражению:

N=N₀e^-kt, (1.6)

которое по математической форме совпадает с эмпирической формулой Резерфорда и Содди (1.1), если принять во внимание, что обозначение коэффициента пропорциональности, введенного в уравнение (1.5), безразлично для смысла получившегося соотношения. Отсюда k ? ? .

В дальнейшем удобно пользоваться постоянным обозначением

– dN/dt = A. (1.7)

Рассматривая формулы (1.2) , (1.6) и (1.7) в совокупности, убеждаемся в справедливости следующих соотношений:

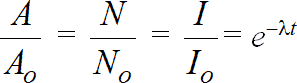, (1.8)

A = A_oe^-?t; N = N₀e^-?t; I = I₀e^-?t ; (1.9)

A = ?N . (1.10)

Можно преобразовать зависимость (1.8), введя иной способ измерения времени: описывая эволюцию (распад) каждого радионуклида, будем измерять время в относительных единицах: n = t/T_1/2, т.е. не в секундах, часах и т.д., а в числах периодов полураспада, что является безразмерным аргументом.

Тогда

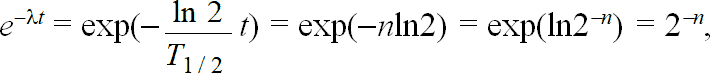
т.е.

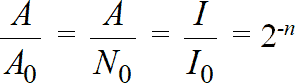. (1.11)

В реальных условиях радионуклиды почти никогда не встречаются в компактном состоянии, являя собой некоторую фазу, все атомные ядра которой радиоактивны и характеризуются одной и той же величиной ?. Обычно атомы радионуклидов так или иначе распределены в некотором стабильном веществе, входя в состав химических соединений, растворов различной природы или более грубых смесей.

В этом случае образец подобного тела (проба, навеска и т.п.), содержащего радионуклид (чаще всего несколько различных радионуклидов), принято называть радиоактивным источником.

Теперь можно ввести понятие активности радионуклида (радионуклидов) в источнике (образце). Это – отношение числа спонтанных ядерных превращений радионуклида (радионуклидов) dN, происходящих в данном источнике (образце) за интервал времени dt, к этому интервалу: A = dN/dt. Здесь нет знака «минус», т.к. dN определено как положительная величина (число превращений), а не как «отрицательное приращение» (т.е. убыль вследствие распада) числа ядер (см. (1.7).

При этом в зависимости от вида радионуклида после слова «активность» следует указывать символ соответствующего радионуклида, например, «активность ²²⁶Ra в источнике», «активность ¹³⁷Cs в растворе» и т.п.

В противоположность инструментальной активности (ее иногда называют относительной) величину A, вводимую формулой (1.7) и сформулированным выше определением, называют абсолютной активностью. Но в профессиональных текстах часто слово «абсолютная» опускается, если из контекста ясно, что речь идет о скорости распада радиоактивной субстанции, происходящего во всем источнике (образце).

Введем еще несколько определений.

Удельная активность радионуклида (радионуклидов): отношение активности радионуклида (радионуклидов) в образце к массе образца или к массе элемента (соединения).

Объемная активность радионуклида (радионуклидов): отношение активности радионуклида (радионуклидов) в образце к объему образца.

Удельная поверхностная активность радионуклида (радионуклидов): отношение активности радионуклида (радионуклидов) в радиоактивном материале, распределенном по данной поверхности, к площади этой поверхности.

Наряду с абсолютной (удельной, объемной и удельной поверхностной) активностью в лабораторной и инженерной практике часто пользуются инструментальной активностью, вводимой так же удельно (т.е. на единицу массы, объема или поверхности).

В соответствии с международной системой единиц (СИ) единицей абсолютной активности является «беккерель» (в честь первооткрывателя радиоактивности Анри Беккереля). Один беккерель (1 Бк) соответствует одному распаду в секунду. До сих пор используется также и исторически первая единица «кюри», допускаемая в качестве внесистемной. Один кюри (1 Kи) соответствует 3,7•10¹⁰ расп/сек (Примерно такое число распадов в секунду наблюдается в 1 г элементарного ²²⁶Ra.). Таким образом,

1Kи= 3,7 • 10¹⁰ Бк. (1.12)

Физический смысл постоянной радиоактивного распада ?, введенной Резерфордом и Содди, можно прояснить следующим образом. Положим в соотношениях (1.8) A/A₀ = N/N₀ = I/I₀ = 0,5. Время, протекшее c момента произвольно выбранного начала отсчета (при t = 0 A = A₀, N = N₀, I = I₀) до момента достижения указанного состояния, называется периодом полураспада и обозначается: t(A/A₀ = N/N₀ = I/I₀ = 1/2) = T_1/2

Отсюда следует: .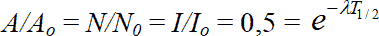

Или, что то же самое: .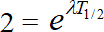

После логарифмирования (в системе натуральных логарифмов) обеих частей последнего равенства получаем соотношение: ln2 = ?T_1/2, откуда следует:

? = ln2/T_1/2. (1.13)

Если положить в общем случае A/A₀ = N/N₀ = I/I_o = 1/n (рассматривать уменьшение начальной активности и начального числа ядер не в два раза, а в n раз), то ? = lnN/T_1/n. Допустим, что n = e (основание натуральных логарифмов). Тогда очевидно, что

? = lne/T_1/e= 1/T_1/e , то есть (1.14)

постоянная радиоактивного распада равна обратному значению отрезка времени, по истечении которого активность радионуклида и число нераспавшихся ядер уменьшаются в e раз. Это время на языке физической статистики называют средним временем жизни атома радиоактивного вещества.

Среднее время жизни равно сумме времен существования всех атомов, деленной на их начальное число (N_o при t =0). Поскольку N является очень большим числом, то эту сумму можно заменить эквивалентным интегралом, полагая N непрерывной функцией от t (как и было принято выше).

Число атомов, распадающихся в промежуток времени между t и t + dt, равно ?Ndt =?N_oe ^{– ?t}dt. Эти атомы имеют продолжительность жизни t. Следовательно, общая продолжительность жизни всех атомов данной группы будет равна t ? N₀ e ^{– ?t}dt.

Суммарную продолжительность жизни (?) всех N₀ атомов можно получить, проинтегрировав полученное выражение по t в пределах от 0 до ?

и поделив его на N₀:

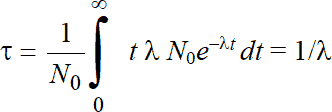, (1.15)

откуда следует, что ? = T_{1/e =} 1/? .

Таким образом, используя соотношения (1.10), (1.13) – (1.15), можно разносторонне интерпретировать физический смысл ? :

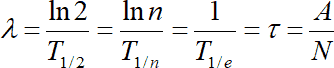(1.16)

Из последнего равенства (? = A/N) следует, что ? можно истолковать как меру, определяющую число актов распада, в единицу времени приходящееся на один атом (атомное ядро) в среднем. Эта мера и есть вероятность распада в единицу времени в собрании N атомов (ядер) в расчете на один атом (ядро).

Отсюда видно, что размерность величины ? – обратные секунды (с ^{– 1}). Табулируют значения констант радиоактивного распада обычно в этих единицах, но гораздо чаще прибегают к понятию «период полураспада» как к интуитивно более понятной величине. При этом выражают его в привычных и обозримых единицах, – от долей секунды до нескольких миллиардов и более лет.

Статистическое обоснование закона радиоактивного распада было предложено Э. Фон Швейдлером в 1905 году. Как только что было выявлено, каждое радиоактивное ядро имеет определенную вероятность распада, а константа ? и есть величина вероятности этого события. Можно показать, что из такого толкования радиоактивности непосредственно следует эмпирически установленный Резерфордом и Содди экспоненциальный закон распада.

Допустим, что вероятность испытать распад в течение некоторого промежутка времени ?t для всех ядер данного радионуклида равна величине w_?t, которая пропорциональна только этому промежутку времени ?t, т.е. w_?t = k?t, где k – коэффициент пропорциональности. Вероятность же пережить этот промежуток времени (т.е. не распасться), как вероятность противоположного события, будет равна 1 – w_?t = 1 – k?t. Вероятность 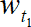пережить некоторый больший промежуток времени t₁ = h?t, где h – произвольное число, будет уже вероятностью сложного события (наступление h раз события, вероятность которого равна 1 – k?t). Эта вероятность в соответствии с теоремой об умножении вероятности выразится следующим образом: w_t1 = (1 – w_?t)^h = (1 – k?t)^h.

Прологарифмируем это равенство: lnw_t1 = hln(1 – k?t).

Пусть при постоянном значении t₁ = h?t ?t стремится к 0. Тогда, полагая слагаемое k?t величиной, пренебрежимо малой по сравнению с единицей, разлагая в ряд ln(1–k?t) по малому параметру и ограничиваясь линейным членом разложения, получим:

lnw_t1 = – hk?t = – kt₁.

Потенцируя это выражение и полагая, что в силу произвольности выбора отрезка времени t₁ индекс «1» не имеет значения, получим:

w_t = e ^{– kt}.

С другой стороны, вероятность атому (ядру) не распасться в течение времени t можно оценить как отношение числа «благоприятных» исходов к их общему числу (в течение времени t каждому атому можно поставить в соответствие только два исхода: он либо распадется, либо не распадется; последний исход и назван здесь «благоприятным»).

Иными словами, если в момент времени, выбранный как начальный (t = 0), существовало N₀ атомов радионуклида, то математическое ожидание числа атомов или среднее число атомов, не распавшихся за время t, будет равно:

N = w_t No= Ne^–kt, (1.17)

а это и есть одно из выражений закона радиоактивного распада (1.9); кроме того, становится очевидным, что коэффициент пропорциональности k, связывающий вероятность ядру испытать распад в течение промежутка времени ?t с его величиной, совпадает с константой радиоактивного распада ? как по статистическому смыслу, так и вследствие изоморфизма уравнений (1.9) и (1.17).

Таким образом, k = w_?t/?t? ? ? A/N, что обсуждено выше (1.16).

Данный текст является ознакомительным фрагментом.