1.3.7. Последовательный радиоактивный распад

1. "Генетическая пара"

Рассмотрим случай, когда продукт распада некоторого радионуклида тоже радиоактивен, но после его распада образуется стабильный изотоп. Будем индексами "1" и "2" помечать параметры и переменные, относящиеся соответственно к "материнскому" и "дочернему" радионуклидам. При этих условиях эволюция "генетической пары" представляет собой вариант классической "бассейновой" задачи: "Прирост числа атомов дочернего радионуклида в единицу времени равен разности скоростей актов распада материнского и дочернего радионуклидов, поскольку скорость распада материнского радионуклида равна скорости возникновения дочернего":

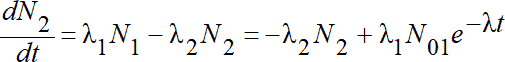. (1.18)

Это линейное неоднородное дифференциальное уравнение первого порядка можно решить, например, методом Лагранжа (метод вариации постоянной). В результате при наложении условия, что при t = 0 N₀₂ = 0 решение (1.18) будет иметь вид:

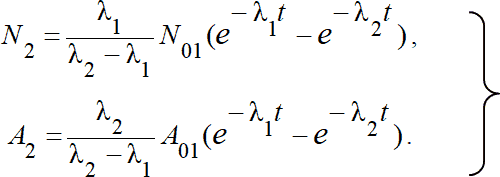(1.19)

Графически эволюция "генетической пары" изображена на рис.1.1.

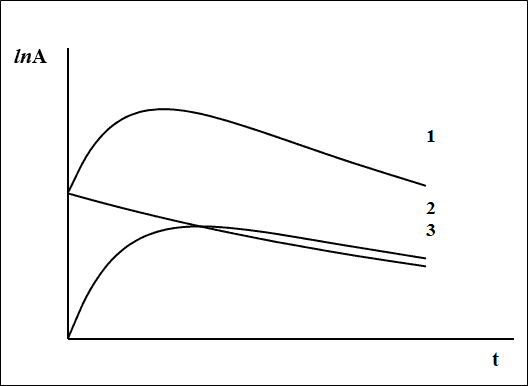
Рис.1.1. Изменение активности при Т₁ >Т₂ (примем условно Т₁=10Т₂): 1 – суммарная активность; 2 – активность дочернего радионуклида; 3 – активность материнского радионуклида.

Важной особенностью взаиморасположения графиков является совпадение точки максимума активности (числа атомов) дочернего радионуклида и точки пересечения графиков A₁(t) и A₂(t) (так же и временных зависимостей N₁ и N₂). В этом можно убедиться, решив соответствующие уравнения: dA₂/dt=0 и A₁=A₂ откуда момент времени (t_max), соответствующий этой точке, определяется следующим образом:

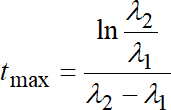. (1.20)

2. Подвижное равновесие

Это состояние в эволюции "генетической пары" достигается только при условии ?₂ > ?₁. В случае ?₂< ?₁ равновесие в любом смысле слова отсутствует, но соотношение (1.20) остается справедливым. Обозначим ?₂ – ?₁ = ? ? и преобразуем (1.11) следующим образом:

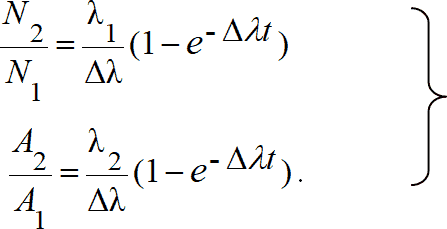. (1.21)

По истечению некоторого времени вследствие монотонного убывания экспоненты можно сделать упрощение 1-е-? ?t H1, приняв заранее определенный уровень погрешности. Но для абсолютного большинства практически интересных случаев можно условно допустить, что этот момент времени совпадает с t_max (см.(1.20)). После упомянутого упрощения соотношения (1.21) приобретают вид:

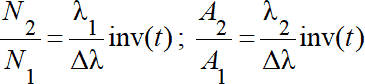, (1.22)

т.е. отношение чисел атомов дочернего и материнского радионуклидов, равно как и значений их абсолютной активности, перестает зависеть от времени, inv (t), в то время как сами значения N₁ , N_2,, A₁ и A₂ продолжают явным образом зависеть от времени.

Таким образом, для "генетической пары" необходимым и достаточным условием наступления подвижного равновесия является неравенство ?₂ > ?₁ (или, что то же самое, T₂ < T₁). Это равновесие наступает не раньше прохождения дочерней активности через максимум и заключается в том, что осуществляются соотношения (1.22). Таким образом, рис.1.1 отражает изменение активности для генетически связанной пары радионуклидов для случая подвижного равновесия.

3. "Вековое" равновесие

Примем более жесткое условие неравенства: ?₂ >> ?₁ (Т₂<<Т₁), но при этом допустим, что период полураспада материнского радионуклида значим в геохронологическом отношении, т.е. уменьшение его активности в технологическом масштабе времени (несколько часов, суток, лет) на точность количественных оценок не влияет. Например, активность радионуклида калий-40 (Т = 1,32·109 лет) по истечению даже миллиона лет уменьшится всего лишь на 0,05%, а за сто лет и вовсе незначимо:5·10–6 %. На этом основании можно принять А₁H const, что позволяет еще более упростить (1.22) следующим образом:

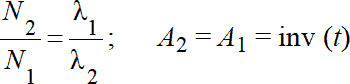. (1.23)

Графически установление векового равновесия для "генетической пары" изображено на рис.1.2.

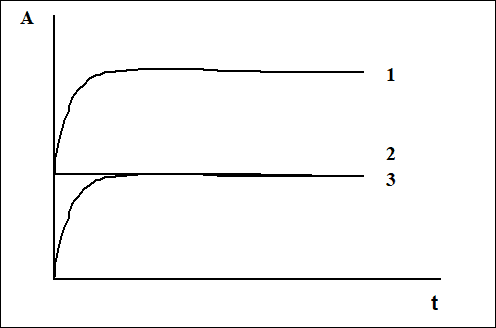
Рис.1.2. Вековое радиоактивное равновесие при Т₁>>Т₂ : 1 – суммарная активность; 2 – активность дочернего радионуклида; 3 – активность материнского радионуклида.

Кинетика установления этого состояния однозначно описывается уравнениями (1.21), которые можно представить в более наглядной форме:

A₂ = A₁ (1–2-n) , (1.24)

где n = t/T₂ – протекшее время, выраженное в единицах периода полураспада дочернего радионуклида. Очевидно, что уже при n = 6 расхождение между A₂ и A₁ составляет всего лишь 1,56%, а при n = 10 менее 0,1%. Таким образом, для "генетической пары" необходимым и достаточным условием наступления векового равновесия является неравенство ?₂ >> ?₁ (Т₂<<Т₁) и практически незначимое уменьшение активности материнского радионуклида в технологическом масштабе времени, A₁ H const (материнский радионуклид должен быть настолько долгоживущим, чтобы оправдалось понятие "векового" равновесия). С погрешностью 1,56 % это равновесие наступает по истечению уже шести периодов полураспада дочернего радионуклида и выражается в равенстве активностей и практической независимости их от времени в технологическом масштабе.

Данный текст является ознакомительным фрагментом.