Игрушечная модель в тридцати двух измерениях

Когда я был маленьким, мне нравилось собирать и разбирать пластиковые модели ракет. Эти модели не могли доставлять спутники на орбиту, не говоря уже о том, чтобы доставить кого-нибудь на Луну. Однако это были вещи, которые я мог держать в руках и с которыми мог играть, а еще они развивали мое воображение. Они были построены в масштабе, и к ним прилагался маленький пластиковый человечек в том же масштабе, что позволяло мне оценить соотношение размеров, понять разницу между перехватчиком и ракетой-носителем, а также разобраться с некоторыми ключевыми понятиями вроде полезной нагрузки и съемных ступеней. Игрушечные модели могут быть интересными и полезными.

Аналогичным образом, для понимания сложных концепций или уравнений могут пригодиться игрушечные модели. Хорошая игрушечная модель создает некоторое представление о реальной вещи, но является достаточно небольшой, чтобы мы могли охватить ее своим сознанием.

В следующих нескольких абзацах я покажу вам игрушечную модель квантовой реальности. Это очень упрощенная модель, но я считаю, что она достаточно сложна, чтобы передать обширность того, что она представляет. Суть в том, что квантовая реальность является ОЧЕНЬ, ОЧЕНЬ БОЛЬШОЙ[36]. Мы создадим игрушечную модель, которая описывает жизнь спинов всего пяти частиц, и обнаружим, что она заполняет пространство 32 измерений.

Начнем с одной квантовой частицы, которая имеет минимальную величину спина. Мы абстрагируемся от всех остальных ее свойств (то есть игнорируем их). Полученный объект называется квантовым битом или кубитом. (Для экспертов: холодный электрон, захваченный в определенном пространственном состоянии, например, с помощью подходящих электрических полей, по сути, является кубитом.) Спин кубита может быть направлен по-разному. Мы напишем: 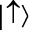для состояния, когда спин кубита определенно направлен вверх, и: 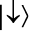для состояния, когда спин кубита определенно направлен вниз.

Кубит также может находиться в состояниях, при которых спин направлен в сторону, и именно здесь начинается все самое интересное. Именно здесь, на данном этапе проявляется основная странность квантовой механики.

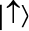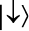Состояния, когда спин направлен в сторону, не являются новыми, независимыми. Эти и все другие состояния кубита представляют собой комбинации состояний и , которые у нас уже есть. Например, состояние, при котором спин направлен на восток, выражается так:

.

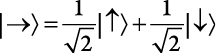Состояние, в котором спин определенно указывает на восток, представляет собой смесь из равных частей северного и южного направлений. При измерении спина в горизонтальном направлении вы всегда будете обнаруживать, что он указывает на восток. Однако если вы измеряете спин в вертикальном направлении, вы с равной вероятностью обнаруживаете, что он указывает либо на север, либо на юг. В этом и заключается смысл этого странного уравнения. Если более подробно, то правило для вычисления вероятности обнаружения определенного результата (спин вверх или спин вниз) при измерении спина в вертикальном направлении заключается в возведении в квадрат множителя, который стоит перед этим состоянием. В данном случае, например, число 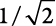умножает состояние «спин вверх», поэтому вероятность обнаружения состояния «спин вверх» составляет .

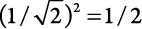Этот пример в миниатюре иллюстрирует компоненты, которые участвуют в описании физической системы, согласно квантовой теории. Состояние системы описывается ее волновой функцией. Вы только что видели волновые функции для трех конкретных состояний. Волновая функция состоит из набора чисел, умножаемых на каждую возможную конфигурацию описываемого объекта. (Это число может быть равно нулю, поэтому, если придираться, мы могли бы написать 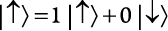.) Число, на которое умножается конфигурация, называется амплитудой вероятности для этой конфигурации. Квадрат амплитуды вероятностей соответствует вероятности наблюдения этой конфигурации.

А как насчет состояния, при котором спин направлен на запад? В силу симметрии это состояние должно иметь равные вероятности для спина вверх и для спина вниз. Однако оно должно отличаться от состояния, при котором спин направлен на восток. Вот как оно выражается:

.

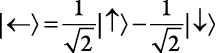Дополнительный знак «?» не влияет на вероятность, поскольку мы возводим число в квадрат. Для восточного и западного направления вероятности одинаковы, однако амплитуды вероятности различны. (Далее мы увидим, к каким последствиям на самом деле приводит знак «?», когда мы будем рассматривать несколько спинов сразу.)

Теперь давайте рассмотрим два кубита. Чтобы получить состояние, при котором оба спина направлены на восток, мы умножаем две копии состояния «спин на восток» и находим:

.

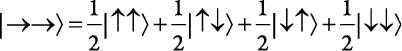Вероятность наблюдения состояния, при котором оба спина направлены вверх, равна (1/2)² = 1/4, как и вероятность состояния «первый спин вверх», «второй спин вниз» и т. д. Аналогичным образом, когда оба спина направлены на запад, мы получаем:

.

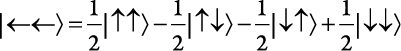Опять же все вероятности обнаружения спинов, направленных вверх и вниз, равны.

Используя только эти два кубита, мы обнаруживаем поистине странное поведение (выражаясь техническим языком, запутанное). Давайте объединим состояние, в котором оба спина направлены на восток, с состоянием, в котором оба направлены на запад. Это можно сделать двумя способами:

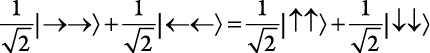(9.1)

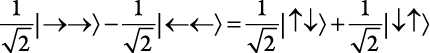(9.2)

В каждом из этих состояний смысл выражений в левой части уравнения заключается в том, что при измерении спинов в горизонтальном направлении мы обнаруживаем: либо оба указывают на восток, либо оба указывают на запад. Каждая из этих возможностей реализуется с вероятностью 1/2. Мы никогда не обнаружим, что один спин указывает на восток, а другой — на запад. Поэтому, когда речь идет об измерениях в горизонтальном направлении, эти два состояния выглядят одинаково. Это все равно, как если бы вы знали, что у вас есть пара носков — либо черных, либо белых, но при этом вы бы не знали, какого именно они цвета. В этом заключается смысл выражений в левой части этих уравнений.

Выражения в правой части сообщают вам, что произойдет, если вы измерите в этих же состояниях оба спина в вертикальном направлении. В этом случае результаты будут совершенно другими. В первом состоянии оба спина будут направлены либо вверх, либо вниз; каждая из этих возможностей может реализоваться с вероятностью 1/2. Второе состояние в рассмотренном выше случае выглядело так же, как первое. Теперь, с другой точки зрения, оно максимально отличается от первого. Во втором состоянии вы никогда не обнаружите, что спины указывают в одном и том же вертикальном направлении: если один направлен вверх, то другой направлен вниз.

Любое из этих состояний вызвало бы недовольство Эйнштейна, Подольского и Розена, поскольку те демонстрируют суть знаменитого ЭПР-парадокса. Измерение спина первого кубита говорит вам о результате, который вы получите, измерив спин второго кубита, на каком бы расстоянии друг от друга они ни находились. На первый взгляд кажется, что это «жуткое действие на расстоянии», как его называл Эйнштейн, способно передавать информацию (то есть сообщить второму спину, куда он должен указывать) со скоростью, превышающей скорость света. Однако это иллюзия, поскольку для того, чтобы два кубита пришли в некоторое конечное состояние, изначально они должны находиться очень близко друг к другу. Позднее мы можем поместить их далеко друг от друга, однако если кубиты не могут двигаться быстрее скорости света, то этого не может и сообщение, переносчиками которого они являются.

В более общем смысле для конструирования всех возможных состояний двух кубитов мы суммируем четыре возможности 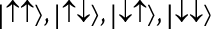, каждая из которых умножается на отдельное число. Это определяет четырехмерное пространство, в котором вы можете передвигаться в четырех различных направлениях.

Описание возможных состояний пяти кубитов подразумевает выбор между вариантами направления вверх и вниз для каждого из них (например, 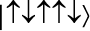или ). Существует 2 ? 2 ? ? 2 ? 2 ? 2 = 32 вероятности, а общее состояние может состоять из вкладов всех состояний, каждый из которых умножается на некоторое число. Вот откуда у нас появляется игрушечная 32-мерная модель. Ничего себе игрушка!