Вывод принципа неопределенности Гейзенберга из теории циферблатов

Вместо того чтобы начать с частицы в определенной точке, подумаем лучше о ситуации, когда мы лишь примерно знаем, где находится частица, но точное ее местоположение неизвестно. Если она где-то в небольшой области пространства, нужно представить ее в виде ряда циферблатов, занимающих всю эту область. В каждой его точке будет находиться по циферблату, и эти циферблаты отразят вероятность, с которой частицу можно найти в этой точке. Если мы возведем в квадрат длины всех стрелок этих циферблатов в каждой точке и сложим, то получим 1, то есть вероятность найти частицу где-то в этой области равна 100 %.

Через некоторое время мы воспользуемся собственными квантовыми правилами для серьезных вычислений, но сначала вынуждены признаться, что забыли упомянуть важное дополнение к правилу поворота стрелок. Мы не хотели вводить его раньше, потому что это чисто техническая деталь, но, если игнорировать ее при вычислении реальных вероятностей, правильных ответов не получим. Относится эта деталь к тому, что написано в конце предыдущего абзаца.

Если начать с одиночного циферблата, стрелка должна иметь длину 1, потому что частица должна находиться в месте расположения циферблата со 100 %-ной вероятностью. Наше квантовое правило гласит: чтобы описать положение частицы в какой-то момент будущего, мы должны переместить циферблат во все точки Вселенной, соответственно тому, как частица может прыгнуть из своего текущего местоположения. Естественно, мы не в силах сделать так, чтобы все стрелки циферблатов имели длину 1, потому что тогда вся интерпретация вероятности рушится. Представьте, например, что частица описывается четырьмя циферблатами, так как находится в четырех разных местах. Если стрелка каждого циферблата имеет длину 1, то вероятность того, что частица находится в любой из четырех позиций, будет равняться 400 % – очевидно, что это нонсенс. Чтобы решить эту проблему, мы должны уменьшать циферблаты, а не только двигать их против часовой стрелки. Это «правило уменьшения» гласит, что после того, как все новые циферблаты будут порождены, каждый из них должен быть разделен на квадратный корень из общего количества часов[11]. Для четырех часов это значит, что каждую стрелку нужно разделить на ?4, то есть стрелка каждого циферблата будет иметь длину ?. Отсюда следует: вероятность того, что частица будет найдена на месте любого из четырех циферблатов, равна (?)2 = 25 %. Таким простым способом мы можем убедиться, что вероятность нахождения частицы где-либо всегда будет 100 %-ной.

Конечно, количество возможных положений может быть бесконечным, так что циферблаты могут оказаться и нулевого размера. Это вызывает тревогу, но математика справится. Для наших целей мы всегда будем считать, что число циферблатов конечно и нам никогда не будет нужно знать, насколько уменьшается каждый циферблат.

Вернемся к предположению, что Вселенная содержит единственную частицу, положение которой точно не известно. Следующий раздел можете воспринимать как небольшую математическую задачу – следить за ходом мысли сначала окажется сложно (тогда попробуйте перечитать), но если вы сможете понять, что происходит, то поймете и то, как возникает принцип неопределенности. Для простоты допустим, что частица движется в одномерном пространстве, то есть находится где-то на прямой линии. Более реалистичный пример для трех измерений не отличается фундаментально, зато его сложнее изобразить. На рис. 4.3 мы сделали зарисовку ситуации одномерного движения, изобразив частицу линией из трех циферблатов. Однако нужно представить, что их намного больше – по одному в каждой точке, где может находиться частица. Просто нарисовать такое количество было бы очень трудно. В этой группе циферблатов, соответствующей исходному положению частицы, циферблат 3 находится слева, а циферблат 1 – справа. Итак, в этой ситуации мы знаем, что частица в начальный момент находится где-то между циферблатами 1 и 3. Ньютон сказал бы, что она останется между циферблатами 1 и 3, если с ней ничего не делать, но как насчет квантового правила? Здесь-то и начинается самое интересное: мы поиграем с правилами циферблатов, чтобы ответить на этот вопрос.

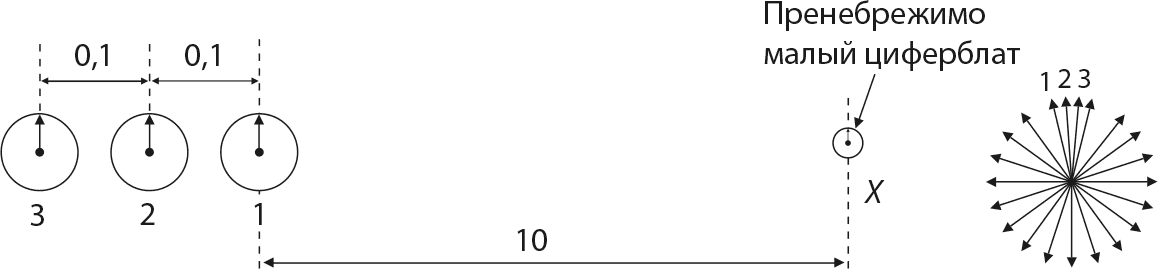
Рис. 4.3. Три циферблата, показывающие одинаковое время и расположенные на одной линии, описывают частицу, в начальный момент находящуюся где-то в области этих циферблатов. Нас интересует, каковы шансы на то, чтобы найти частицу в точке X в некоторый последующий момент времени

Позволим времени идти вперед и выясним, что произойдет с этим рядом циферблатов. Представим себе сначала одну конкретную точку на большом расстоянии от исходной группы циферблатов. На рисунке она отмечена буквой X. О точных параметрах «большого расстояния» поговорим чуть позже, а сейчас это просто значит, что стрелки должны существенно изменить свое положение.

Применив правила игры, мы должны перенести каждый циферблат из исходной группы в точку Х, передвигая стрелки и уменьшая их соответствующим образом. Физически это соответствует тому, что частица прыгает из точки поля в точку Х. В точку Х прибудет несколько циферблатов – по одному из каждой исходной точки, и следует сложить их все. В итоге квадрат длины результирующей стрелки циферблата в точке Х даст нам вероятность нахождения частицы в Х.

Теперь понаблюдаем за процессом в развитии и добавим ряд цифр. Допустим, что точка Х находится на расстоянии 10 единиц от циферблата 1, а ширина области, занимаемой исходной группой циферблатов, – 0,2 единицы. При ответе на очевидный вопрос «Что это за расстояние – 10 единиц?» в наше повествование входит постоянная Планка, но сейчас мы ловко отпихиваем ее в сторону и просто отмечаем, что 1 единица расстояния соответствует 1 полному (12-часовому) обороту стрелки на циферблате. Это значит, что точка Х примерно в 10? = 100 полных оборотах от изначального поля (помните о правиле хода часов). Положим также, что циферблаты в исходной группе были одного размера и все указывали на 12 часов. Предположение об их одинаковом размере – это предположение о том, что частицу можно с одинаковыми шансами найти в точках, соответствующих циферблатам 1, 2 и 3 на нашем рисунке, а значение того, что все циферблаты показывают одинаковое время, выявится позднее.

Чтобы переместить циферблат из точки 1 в точку Х, нужно в соответствии с правилом сделать полный оборот стрелки против хода часов 100 раз. Сейчас перенесемся в точку 3, которая находится в 0,2 единицы от точки 1, и переместим в Х и этот циферблат. Так как этот циферблат должен пройти 10,2 единицы, открутить его стрелку назад нужно чуть дальше – 10,2? раза, что очень близко к 104.

Теперь у нас два циферблата в точке Х, соответствующие частице, прибывшей туда из точки 1, и частице, прибывшей из точки 3. Их нужно сложить, чтобы начать вычислять итоговый циферблат. Поскольку обе стрелки были откручены назад примерно одинаковое количество раз, то они оба показывают приблизительно 12 часов. При сложении они дают часы с более длинной стрелкой, тоже указывающей на 12. Заметьте, роль играет только конечное положение часовой стрелки. Нет смысла фиксировать число ее оборотов. Пока все хорошо, но мы еще не закончили, потому что между правым и левым краями исходной группы еще есть множество маленьких циферблатов.

И мы переводим внимание на циферблат, лежащий посредине исходной группы, то есть в точке 2. Этот циферблат находится в 10,1 единицы от Х, то есть нужно совершить 10,12 оборота стрелки. Это очень близко к 102 полным оборотам, то есть снова получается целое число. Нужно прибавить этот циферблат к остальным из точки Х, и, как и в предыдущий раз, стрелка станет длиннее. Продолжим: есть точка между точками 1 и 2, и при перемещении циферблата в точку Х нужно будет сделать 101 полный оборот, что снова удлинит стрелку получающегося циферблата. И тут наступает важный момент. Если обратиться к циферблату между этими двумя, то его нужно будет подкрутить 100,5 раза до достижения точки Х. Таким образом получится циферблат, стрелка которого укажет на 6 часов, и при сложении мы уменьшим длину стрелки в Х. Немного подумав, вы убедитесь, что, хотя точки, отмеченные как 1, 2 и 3, дают в Х циферблаты, указывающие на 12, как и точки, лежащие между 1–2 и 2–3, но точки, лежащие на ? и ? пути между 1–3 и 2–3, дают циферблаты, указывающие на 6. Всего получается 5 циферблатов со стрелкой вверх и 4 циферблата со стрелкой вниз. При сложении всех этих циферблатов мы получим в точке Х такой циферблат, стрелка которого будет микроскопической, потому что почти все циферблаты будут отменять друг друга.

Такое «аннулирование циферблатов», разумеется, относится и к более реалистическому случаю, когда мы принимаем во внимание абсолютно все точки, лежащие в области между точками 1 и 3. К примеру, точка, лежащая на ? пути от точки 1, дает циферблат со стрелкой на 9 часов, в то время как точка, лежащая на ? пути, указывает на 3 часа – и снова они отменяют друг друга. В суммарном итоге оказывается, что циферблаты, соответствующие всем возможным для частицы маршрутам из любой точки поля в точку Х, отменяют друг друга. Аннулирование показано в правом углу рисунка. Стрелки соответствуют часовым стрелкам, прибывающим в Х из различных точек исходной области.

В результате сложения всех этих стрелок они отменяют друг друга. Это основной момент, который нужно усвоить.

Итак, повторим: мы сейчас показали, что, если исходная группа циферблатов достаточно велика и точка Х достаточно далека, то для каждого циферблата, прибывающего в Х со стрелкой на 12 часов, найдется другой циферблат со стрелкой на 6 часов, отменяющий предыдущий. Для каждого циферблата со стрелкой на 3 часа найдется другой со стрелкой на 9 часов, отменяющий первый, и т. д. Эта массовая отмена подразумевает, что на самом деле нет практически никаких шансов найти частицу в точке Х. Звучит это очень интересно и вдохновляюще, так как кажется, что описание соответствует неподвижной частице. Начав со смехотворного на вид предположения о том, что частица может перемещаться из любой точки пространства в любое другое место Вселенной за очень короткий срок, мы обнаруживаем, однако, что это не так, если начать с группы циферблатов. В ситуации, когда все циферблаты интерферируют друг с другом, частица практически не имеет возможности сдвинуться далеко от исходного положения.

Этот вывод, по словам профессора Оксфордского университета Джеймса Блайни, стал результатом «неконтролируемой квантовой интерференции». Для этого явления и соответствующей ему взаимной отмены циферблатов точка Х должна быть достаточно далека от исходной области, – настолько, чтобы циферблаты могли совершить достаточное количество оборотов. Почему? Потому что если точка Х расположена слишком близко, то стрелки часов, возможно, не успеют сделать даже один оборот, а следовательно, не будут отменять друг друга столь эффективно. Представим, например, что расстояние между циферблатом в точке 1 и точкой Х не 10 единиц, а 0,3 единицы. Теперь стрелка циферблата на передней стороне области повернется меньше, чем в предыдущем случае, совершая всего 0,3? = 0,09 оборота, и укажет на начало второго. Аналогично стрелка циферблата из точки 3 на задней стороне области совершит 0,5? = 0,25 оборота и укажет на 3 часа. Соответственно, все циферблаты в Х укажут на что-то между часом и тремя, то есть больше не отменяют друг друга, а складываются в один большой циферблат, указывающий приблизительно на 2 часа. Все это говорит о том, что существует довольно весомый шанс нахождения частицы в местах, расположенных вблизи от исходной области, но все же вне ее. Под «вблизи» мы понимаем расстояние, недостаточное для того, чтобы получить по меньшей мере один оборот стрелки часов. Все это уже намекает на принцип неопределенности, но по-прежнему выглядит довольно туманно, поэтому давайте разберемся, что именно мы понимаем под «достаточно большой» исходной областью и «достаточно удаленной» от него точкой.

Вслед за Дираком и Фейнманом мы сделали предположение, что, если частица массой m проходит расстояние x за время t, величина поворота стрелок будет пропорциональна действию, то есть mx? / t. Однако слова «пропорциональна» недостаточно, если нужно рассчитать реальные величины. Нужно точно знать, чему равен поворот стрелок. В главе 2 мы говорили о законе всемирного тяготения Ньютона и для точных количественных прогнозов ввели понятие гравитационной постоянной Ньютона, которая определяет величину силы гравитации.

С помощью добавления в уравнение постоянной Ньютона можно подставлять числа в уравнение и вычислять характеристики реальных физических явлений, например период обращения Луны по орбите или маршрут движения космического корабля «Вояджер-2» по Солнечной системе. Но нам нужно что-то подобное и для квантовой механики – такая природная константа, которая «задает масштаб» и позволяет нам взять величину действия и выдать точное предсказание того, сколько оборотов должны сделать часовые стрелки при перемещении частицы на конкретное расстояние из исходного положения за заданное время. Эта константа называется постоянной Планка.