3.2. Несимметричность взаимных превращений теплоты и работы. Принцип Карно

3.2. Несимметричность взаимных превращений теплоты и работы. Принцип Карно

Второй закон термодинамики, так же как и первый, формировался в течение длительного периода трудами многих ученых и инженеров. Без его использования дальнейшее развитие теплоэнергетики, химической технологии и многих других направлений техники и науки было бы невозможным.

Установление общности и количественной эквивалентности различных форм движения, а затем точное формулирование на этой основе первого закона термодинамики было необходимо, но недостаточно. Нужно было установить условия, определяющие возможности перехода одних форм энергии в другие и прежде всего теплоты в работу. Практика показывала, что представление о всеобщей превратимости, эквивалентности (т.е. равноценности) различных видов энергии нуждается в уточнении даже применительно к таким ее формам, как теплота и работа. Действительно, почему переход работы в теплоту совершается очень просто, не вызывая никаких затруднений? Еще на заре цивилизации человек добывал огонь трением, производя безо всякой науки именно такое преобразование. Однако превратить теплоту в работу удалось (если не считать античных паровых игрушек вроде «эолопила» Герона) с большим трудом только во второй половине XVIII в., когда были созданы паровые машины. И дело было здесь не в технической сложности этих машин (хотя это тоже сыграло свою роль), а в принципиальной трудности такого превращения, неясности условий, необходимых для него.

Впервые правильно поставил и решил эту задачу С. Карно, о котором мы уже писали в связи с первой формулировкой закона сохранения энергии. Со знаменитой книги Карно «О движущей силе огня…» начинается не только история термодинамики, но и вся современная теоретическая теплоэнергетика[46].

По теории теплорода работа паровой машины выглядела очень просто. Теплород от дымовых газов, полученных при сжигании топлива, переходил к воде при высокой температуре, превращая ее в пар. Пар расширялся в цилиндре, производя работу. Затем пар направлялся в конденсатор, где при низкой температуре отдавал теплород охлаждающей воде.

Схема такой машины показана на рис. 3.1,а; поток теплорода Q (ширина полосы соответствует его количеству) «падает» с температуры Т₁ на более низкую температуру Т₂ < Т₁. При этом производится работа L. Нетрудно видеть, что такое объяснение работы тепловой машины возникло по аналогии с гидравлической машиной (например, водяной мельницей); только роль воды играет «теплород», а напора, обусловленного высотой падения воды ?h = h₁ — h₂ — разность температур ?T = T₁—T₂ (рис. 3.1, б). Количество воды G, как и количество теплорода Q, не меняется — сколько входит (Q₁), столько и выходит (Q₂). На первых порах такая теория была вполне приемлемой, тем более что из нее следовал правильный и очень важный вывод: тепловая машина может работать только при наличии разности температур. Если ?T = 0, то теплота будет «мертвой», как «мертвая вода» Леонардо да Винчи при ?h = 0.

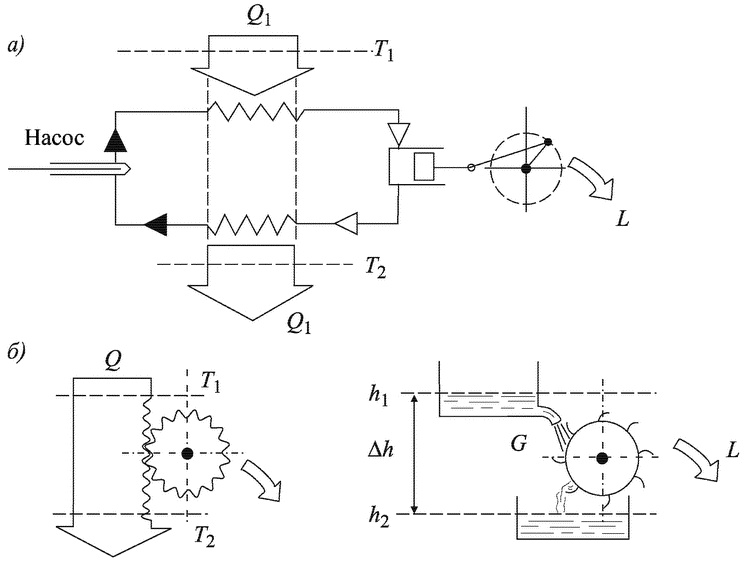
 ^{Рис. 3.1. Схема действия паровой машины (двигателя) с позиций теории теплорода: а — «падение теплорода» с температуры Т₁ до температуры Т₂, б — механическая и гидравлическая аналогии}

У современного читателя, однако, может возникнуть естественный вопрос. Пусть инженеры того времени и не знали закона сохранения энергии, но ведь он все равно действовал! А это означает, что количество отдаваемого внизу при T₂ теплорода (т. е. теплоты) должно было быть существенно меньше, чем то, которое поступило наверху при T₁, на количество произведенной работы, т. е. Q₂ = Q₁ — L.

Как же не заметили этого? Ответ очень прост. Самые лучшие паровые машины того времени имели очень малую эффективность: они превращали в работу не более 3-5% получаемой теплоты. А это означает, что Q₂ отличалось от Q₁ так, как 95 отличается от 100; но точность тепловых измерений в то время была намного меньше 5%. Поэтому разницу между Q₁ и Q₂ просто не могли заметить (тем более что никому не приходило в голову, что ее нужно искать).

С. Карно поставил перед собой задачу определить количественно «движущую силу огня», т. е., говоря современным языком, то максимальное количество работы, которое может дать единица количества теплоты.

Несмотря на то, что С. Карно исходил в этой работе еще из теории теплорода, а закон сохранения движущей силы (т. е. энергии)[47] он сформулировал позже — между 1824 и 1832 гг. — он блестяще решил задачу.

Позднейшим исследователям оставалось лишь придать математическую форму положениям Карно и развить их применительно к новым научным фактам, изложив их с учетом первого закона. Только через четверть века термодинамика пошла дальше, но основные идеи Карно остались незыблемыми. Такая поразительная устойчивость основных положений С. Карно (свойственная вообще великим научным открытиям) связана с тем, что он подошел к задаче с максимально общих позиций, исключив все частности, не имеющие принципиального значения. Он рассматривал не какую-то определенную паровую машину, даже не паровую машину вообще, а абстрактный, идеальный тепловой двигатель, результаты действия которого не зависят от его конструкции. Для этого он ввел специальный цикл, впоследствии названный его именем.

Из многочисленных следствий работы С. Карно для нашей цели — анализа ppm-2 — наиболее важно положение о том, что для непрерывной работы теплового двигателя необходим источник теплоты с более высокой температурой и теплоприемник с более низкой — так называемый принцип Карно. Математическое выражение принципа Карно, определяющее условия перехода теплоты Q в работу L при заданных температурных условиях, было выведено Р. Клаузиусом в виде предельно простой, широко известной формулы

L = Q₁?(T₁ – T₂)/T₁  (3.1)

Здесь, как и на рис. 3.1, высокая температура Т₁ в Кельвинах соответствует подводу теплоты Q₁ к двигателю, а более низкая Т₂ — та, при которой теплота отдается. Из формулы (3.1) прямо следуют многие важные следствия. Для нас имеют значение два вывода.

Первый вывод состоит в том, что получаемая работа всегда меньше подводимой к двигателю теплоты Q. Действительно, коэффициент Карно (Т₁ — Т₂)/Т₁ (или 1 — T₂/T₁) всегда меньше единицы. Другими словами, в работу может быть превращена только часть получаемой теплоты; другая часть, равная Q₂ = Q₁ — L, неизбежно должна быть отдана какому-либо теплоприемнику[48] при температуре Т₂. Чем выше температура Т₁ и ниже Т₂, тем большая доля теплоты Q₁ может быть превращена в работу. Но всю теплоту Q₁ в работу преобразовать нельзя (для этого Т₁ должна была бы быть бесконечно большой или Т₂ бесконечно малой).

Так, например, если Т₁ = 1200 К, а T₂ = 300 К, то из 100 кДж теплоты может быть получено (1200 – 300)/1200 кДж = 75 кДж работы. Остальные 25 кДж могут быть отведены только в виде теплоты Q₂ < Q₁ при температуре Т₂ = 300 К.

Таким образом, из принципа Карно следует, что превратить теплоту в работу полностью нельзя. Следовательно, в природе существует асимметрия во взаимной превратимости теплоты и работы: работа в теплоту может превратиться полностью, но теплота в работу — только частично. Другая, непревратимая часть теплоты неизбежно отводится из двигателя к теплоприемнику (но при более низкой температуре).

Второй вывод из принципа Карно состоит в том, что получение работы из теплоты возможно только в том случае, когда между теплоотдатчиком и теплоприемником есть разность температур (т. е. Т₁ > T₂). Действительно, из формулы (3.1) следует, что чем меньше разность Т₁ — Т₂, тем меньшая доля теплоты Q может быть превращена в работу. Если же Т₁ = Т₂, т. е. если двигатель вступает в тепловой контакт с телами, имеющими одну и ту же температуру, то никакой работы он произвести не может (Т₁ — T₂ = 0, и, следовательно, L = 0 при любом Q).

Никакими ухищрениями обойти оба эти следствия из принципа Карно нельзя.

Второй вывод из принципа Карно убивает наповал идею о двигателе, работающем за счет теплоты, получаемой из равновесной окружающей среды (ppm-2).

Как бы ни была велика связанная с хаотическим тепловым движением молекул внутренняя энергия, содержащаяся в окружающей среде[49], она неработоспособна, ибо в этом случае в нашем распоряжении есть только одна температура — окружающей среды T_О.С..

Таким образом, само по себе наличие энергии еще не говорит о том, что может быть получена работа: энергия может быть и неработоспособной. Поэтому определение энергии, которое еще встречается в некоторых книгах и даже учебниках, как «величины, характеризующей способности тела (или системы) производить работу», в общем случае неверно. Оно досталось по наследству от XVII-XVIII вв., когда представление об энергии (по тогдашней терминологии — «силе») было связано только с механической работой. Принцип Карно ясно показывает, что такое определение (во всяком случае, применительно к внутренней энергии тела и к теплоте, отводимой от него) неверно.

Вокруг нас в воздухе, воде, почве содержится гигантское количество внутренней энергии хаотического молекулярного движения, но, увы, она вопреки надеждам изобретателей ppm-2 для получения работы абсолютно бесполезна. Это утверждает принцип Карно, вытекающий из второго закона термодинамики.

Из всего изложенного неизбежно следует, что единственный способ обоснования возможности «извлекать тепловую энергию из окружающего пространства» и получать из нее работу состоит в низвержении второго закона термодинамики. Вокруг этой крепости — второго закона — и развертывают все баталии изобретатели и теоретики ppm-2.

Чтобы разобраться во всем этом и показать безнадежность попыток опровергнуть второй закон, нужно рассмотреть некоторые его положения, не ограничиваясь принципом Карно. Особое внимание следует уделить вопросу об энтропии — величине, занимающей центральное место в концепции второго закона. На ее долю выпадает максимальное количество атак, кривотолков и даже нехороших слов. Один из ее противников назвал ее даже «ржавым замком», который запирает ворота на пути дальнейшего движения науки.