Глава 27 ЭНЕРГИЯ ПОЛЯ И ЕГО ИМПУЛЬС

Глава 27

ЭНЕРГИЯ ПОЛЯ И ЕГО ИМПУЛЬС

§ 1. Локальные законы сохранения

§ 2. Сохранение энергии и электромагнитное поле

§ 3. Плотность энергии и поток энергии в электромагнитном поле

§ 4. Неопределенность энергии поля

§ 5. Примеры потоков энергии

§ 6. Импульс поля

§ 1. Локальные законы сохранения

То, что энергия вещества не всегда сохра­няется, ясно как день. При излучении света объект теряет энергию. Однако потерянную энергию можно представить в какой-то другой форме, скажем, в форме энергии света. Поэтому закон сохранения энергии не полон, если не рассмотреть энергию, связанную со светом, в частности, и с электромагнитным полем вооб­ще. Сейчас мы подправим его, а заодно и закон сохранения импульса с учетом электромагнит­ного поля. Мы, разумеется, не можем обсуждать их порознь, ибо, согласно теории относитель­ности, это различные проявления одного и того же четырехвектора.

С сохранением энергии мы познакомились еще в начале нашего курса; тогда мы просто сказали, что полная энергия в мире остается постоянной. Теперь же мы хотим сделать очень важное обобщение идеи закона сохранения энергии, которое скажет нам нечто о деталях того, как это происходит. Новый закон будет говорить, что если энергия уходит из какой-то области, то это может происходить только за счет ее вытекания через границы рассматрива­емой области. Это утверждение сильнее, чем просто сохранение энергии без подобных огра­ничений.

Чтобы легче понять смысл этого утверждения, посмотрим, как работает закон сохранения заряда. У нас есть плотность тока j и плотность заряда r, а сохранение заряда описывается тем, что если в каком-то месте заряд уменьшается, то оттуда должен происходить отток зарядов. Мы называем это сохранением заряда. Математически закон сохранения записывается в виде

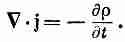
(27.1)

Как следствие этого закона полный заряд всего мира остается постоянным. Заряды никогда не рождались и не уничтожались; в мире как целом нет никакой чистой прибыли зарядов, как нет и никаких потерь. Однако полный заряд мира можно сде­лать постоянным и другим способом. Пусть вблизи точки (1) находится заряд Q₁ , а вблизи точки (2), расположенной от нее на некотором расстоянии, никакого заряда нет (фиг. 27.1). Предположим теперь, что с течением времени заряд Q₁посте­пенно исчезает, но что одновременно с уменьшением Q₁ вблизи точки (2) появляется заряд Q₂, причем так, что в любой момент сумма Q_tи Q₂остается постоянной. Другими словами, в любой промежуточный момент количество заряда, теряемое Q₁ , при­бавляется к Q₂. При этом в мире полное количество заряда сох­раняется. Хотя это тоже «всемирное» сохранение заряда, мы не будем его называть «локальным» сохранением, ибо для того, чтобы заряд перебрался из точки (1) в точку (2), ему не обяза­тельно появляться где-то в пространстве между этими точками. Локально заряд просто «теряется».

Однако такой «всемирный» закон сохранения встречает в теории относительности большие трудности. Понятие «одно­временно» для точек, разделенных расстоянием, неэквивалентно для разных систем. Два события, происходящие одновременно в одной системе, не будут одновременными в системе, движу­щейся относительно нее. Для «всемирного» сохранения только что описанного типа требуется только одно—чтобы заряд, те­ряемый Q₁, одновременно появлялся в Q₂. В противном случае будут такие моменты, когда заряд не сохраняется. По-видимому, способа сделать закон сохранения заряда релятивистски инвариантным, не делая его «локальным», не существует.

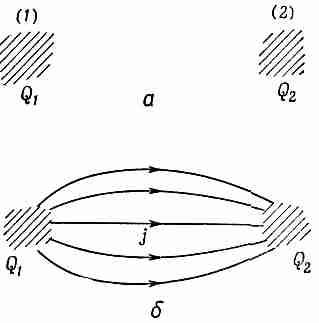
Фиг. 27.1. Два способа описания сохранения заряда

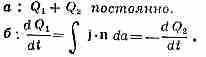
Суть в том, что требование лоренцевой инвариантности, как оказы­вается, удивительнейшим образом ограничивает возможные законы природы. В современной квантовой теории поля, на­пример, теоретики часто пытаются изменить теорию, допустив то, что мы называем «нелокальным» взаимодействием, когда нечто, находящееся здесь, непосредственно влияет на нечто, находящееся там, но мы всегда наталкиваемся на трудности, связанные с принципами относительности.

«Локальные» же законы сохранения основаны на другой идее. Они утверждают, что заряд может перейти из одного места в другое только при том условии, что нечто такое происходит в пространстве между ними. Чтобы описать такой закон, нам нужна не только плотность заряда r, но и величина другого сор­та, именно вектор j, задающий скорость потока заряда через поверхность. При этом поток связан со скоростью изменения заряда уравнением (27.1). Это более сильная формулировка закона сохранения. Она говорит, что заряд сохраняется особым образом, сохраняется «локально».

Сохранение энергии, оказывается, тоже локальный процесс. В мире существует не только плотность энергии в данной об­ласти, но и вектор, представляющий скорость потока энергии через поверхность. Например, когда источник излучает свет, мы можем найти энергию света, излучаемого им. Если мы вообра­зим некую математическую поверхность, окружающую источ­ник света, то потеря энергии этого источника равна потоку энергии через окружающую его поверхность.

§ 2. Сохранение анергии и электромагнитное поле

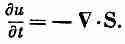
Нам надо теперь описать сохранение энергии в электромаг­нитном поле количественно. Для этого нужно выяснить, сколько энергии находится в единице объема, а также какова скорость ее потока. Рассмотрим сначала энергию только электромагнит­ного поля. Пусть и обозначает плотность энергии поля, т. е. количество энергии в единице объема пространства, а вектор S — поток энергии поля (т. е. количество энергии, прошедшее в единицу времени через единичную поверхность, перпендику­лярную к потоку). Тогда, аналогично сохранению заряда (27.1), можно написать «локальный» закон сохранения энергии поля в виде

(27.2)

Конечно, этот закон, вообще говоря, не верен; энергия поля не сохраняется. Представьте, что вы находитесь в темной комнате, а затем поворачиваете выключатель. Комната внезапно наполняется светом, т. е. в ней оказывается энергия поля, ко­торой раньше не было. Уравнение (27.2) не составляет полного закона сохранения, ибо энергия одного только поля не сохра­няется, а существует еще энергия вещества; сохраняется лишь полная энергия во всем мире. Энергия поля будет изменяться, если оно производит работу над веществом или вещество произ­водит работу над полем.

Однако если внутри интересующего нас объема находится вещество, то мы знаем, сколько энергии оно несет в себе: энергия каждой частицы равна m₀c²/Ц(l-v²/c²). Полная же энергия вещества равна просто сумме энергий всех частиц, а поток ее через поверхность равен просто сумме энергий, переносимой каждой частицей, пересекающей эту поверхность. Но сейчас мы будем иметь дело только с энергией электромагнитного поля: Так что мы должны написать уравнение, которое говорит, что Г полная энергия поля в данном объеме уменьшается либо в ре­зультате вытекания ее из объема, либо потому, что поле передает свою энергию веществу (или приобретает ее, что означает просто отрицательную потерю). Энергия поля в объеме V равна

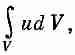
а скорость ее уменьшения равна производной этого интеграла по времени со знаком минус. Поток энергии поля из объема V равен интегралу от нормальной компоненты S по поверхности 2, ограничивающей объем V:

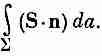
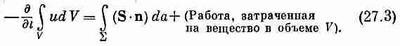
Таким образом,

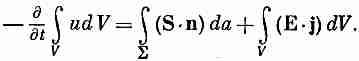
Раньше мы видели, что над каждой единицей объема вещества поле в единицу времени производит работу Е·j. [Сила, действу­ющая на частицу, равна F=q(E+vXB), а мощность равна F-v=qE·v. Если в единице объема содержится N частиц, то эта мощность в единице объема равна NqE·v, a Nqv=j·I Таким образом, величина Е·j должна быть равна энергии, теряемой полем в единице объема за единицу времени. Уравнение (27.3) при этом приобретает вид

(27.4)

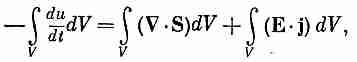
Вот как выглядит наш закон сохранения энергии в поле. Его можно записать как дифференциальное уравнение, подобное (27.2); для этого второе слагаемое нужно превратить в интеграл по объему, что легко делается с помощью теоремы Гаусса. По­верхностный интеграл от нормальной компоненты S равен интегралу от дивергенции S по объему, ограниченному этой поверхностью, так что уравнение (27.3) эквивалентно следую­щему:

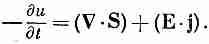
где производную по времени от первого слагаемого мы внесли под интеграл. Поскольку это уравнение верно для любого объема, то интегралы можно отбросить и получить уравнение для энергии электромагнитного поля:

(27.5)

Однако это уравнение не даст нам ничего хорошего, пока мы не узнаем, что такое u и S. Быть может, мне следовало бы просто сказать вам, как они выражаются через Е и В, поскольку это единственное, что нам, собственно, нужно. Однако мне очень хочется изложить вам все те рассуждения, которыми в 1884 г. воспользовался Пойнтинг, чтобы получить формулы для S и u, с тем, чтобы вы понимали, откуда они взялись. (Для дальнейшей работы, впрочем, вам этот вывод не потребуется.)

§ 3. Плотность энергии и поток энергии в электромагнитном поле

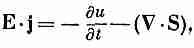
Идея заключается в том, что должны существовать плот­ность энергии u и поток S, которые зависят только от полей Е и В. [В электростатике, например, плотность энергии, как мы знаем, можно записать в виде ¹/₂e₀(Е·Е).] Разумеется, u и S могут зависеть от потенциалов и чего-то другого, но давайте лучше посмотрим, что мы можем написать. Попытаемся перепи­сать величину Е·j в таком виде, чтобы она стала суммой двух слагаемых, одно из которых было бы производной по времени от некоторой величины, а второе — дивергенцией. Тогда первую величину мы бы назвали и, а вторую — S (разумеется, с надле­жащими знаками). Обе величины должны быть выражены только через поля, т. е. мы хотим записать наше равенство в виде

(27.6)

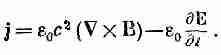
причем левая часть уравнения должна выражаться только через поля. Как это сделать? Разумеется, нужно воспользоваться уравнениями Максвелла. Из уравнения для ротора В имеем

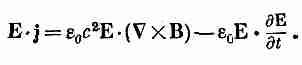
Подставляя это в (27.6), получаем выражение его только через Е и В:

(27.7)

Работа частично нами уже закончена. Последнее слагаемое есть производная по времени — это (д/дt)(¹/₂e₀Е·Е).

Итак, ¹/₂e₀Е·Е должно быть по крайней мере частью u. Такое же выражение получалось у нас и в электростатике. А теперь единственное, что нам остается сделать,— это превра­тить в дивергенцию чего-то второе слагаемое.

Заметьте, что первое слагаемое в правой части (27.7) пере­писывается в виде

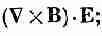
(27.8)

вы знаете из векторной алгебры, что (aXb)·c равно а·(bXc), поэтому первое слагаемое принимает вид

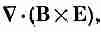
(27.9)

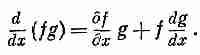
т. е. получилась дивергенция «чего-то», к которой мы так стре­мились. Получилась, но только все это неверно! Я предупреждал вас, что оператор С только «похож» на вектор, а на самом деле он не «настоящий» вектор. Вспомните, что в дифференциальном исчислении существует дополнительное соглашение: когда опе­ратор производной стоит перед произведением, он действует на все стоящее правее него. В уравнении (27.7) оператор С дей­ствует только на В и не затрагивает Е. Но если бы мы записали его в форме уравнения (27.9), то общепринятое соглашение гово­рило бы, что Сдействует как на В, так и на Е. Так что это не одно и то же. В самом деле, если расписать С·(ВXЕ) по ком­понентам, то можно убедиться, что оно равно E· (СXB) плюс какие-то другие слагаемые. Это напоминает взятие производной от произведения в обычном анализе. Например,

Вместо того чтобы выписать все компоненты С· (BXE), мне бы хотелось показать вам один трюк, очень полезный в за­дачах такого рода. Он позволит вам всюду в выражениях, содер­жащих оператор С, пользоваться правилами векторной алгебры, не попадая впросак. Трюк состоит в отбрасывании (по крайней мере на время) правил дифференциального исчисления относи­тельно того, на что действует оператор производной. Вы знаете, что порядок сомножителей важен в двух различных случаях. Во-первых, в дифференциальном исчислении: f(d/dx)g не то же самое, что g(d/dx)f; и, во-вторых, в векторной алгебре: aXb отличается от bXа. Мы можем, если захотим, на минуту отка­заться от правил дифференциального исчисления. Вместо того чтобы говорить, что производная действует на все стоящее правее от нее, мы примем новое правило, избавляющее нас от порядка, в котором записаны сомножители. После этого мы можем крутить ими, как хотим, без всяких помех.

Вот наше новое правило: с помощью индекса мы будем ука­зывать, на что же именно действует дифференциальный опера­тор; при этом порядок сомножителей не имеет никакого значе­ния. Допустим, что оператор д/дх мы обозначили через D. Тогда символ D_fговорит, что берется производная только функции

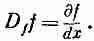
Но если мы имеем выражение D_ffg, то оно означает

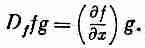
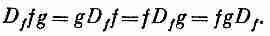
Заметим теперь, что, согласно нашему новому правилу, fD_fg означает то же самое. Одно и то же выражение можно записать любым из следующих способов:

Вы видите, что D_fможет стоять даже после всего. (Странно, почему такому удобному обозначению обычно не учат в книгах по математике и физике.)

Вы, пожалуй, удивитесь: а что, если я хочу написать произ­водную от fg? Если мне нужна производная от обоих членов? Это очень легко: вы пишете D_f(fg)+D_g(fg),т.e.g(df/dx)+f(dg/dx), что в старых обозначениях как раз равно d(fg)/dx.

Вы сейчас увидите, как просто теперь получить новое выра­жение для С·(ВXЕ). Начнем с перехода к новому обозначению и напишем

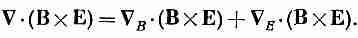
(27.10)

Как только мы сделали это, уже нет больше нужды придержи­ваться строгого порядка. Мы всегда знаем, что С_E действует только на Е, a С_B действует только на В. При этих обстоятель­ствах оператором С можно пользоваться как обычным вектором. (Разумеется, после того как все будет окончено, нам захочется вернуться к «стандартным» обозначениям, которые обычно используются.) Таким образом, теперь мы можем делать различ­ные перестановки сомножителей. Так, средний сомножитель в уравнении (27.10) можно переписать как Е·(С_BXВ). [Надеюсь, вы помните, что a·(bXc) = b·(cXa).] А последний — как В·(EXС_E). Хотя это выглядит несколько странно, но тем не менее здесь все в порядке. Если же мы теперь попытаемся вер­нуться к старым обозначениям, то должны будем расположить операторы С так, чтобы они действовали на свои «собственные» переменные. В первом из них все в порядке, так что мы можем просто опустить индекс у С. Второй же требует некоторой реорганизации, чтобы оператор С поставить перед Е. Этого можно

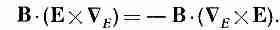
добиться, переставляя сомножители в векторном произ­ведении и меняя знак:

Теперь все стоит на своем месте и можно вернуться к обычным обозначениям. Формула (27.10) эквивалентна следующему равенству:

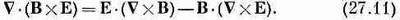
(В этом специальном случае быстрее было бы использовать ком­поненты, но, право же, стоило потратить время ради того, чтобы показать вам математический трюк. Может случиться, что вы больше нигде его не встретите, а он очень удобен тогда, когда в векторной алгебре нужно освободиться от правила порядка членов при дифференцировании.)

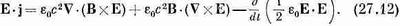
Вернемся теперь к нашему закону сохранения энергии, при­чем для преобразования СXB в (27.7) мы используем новый результат — равенство (27.11). Вот что оно дает:

Теперь вы видите, что мы почти у цели. Одно из наших сла­гаемых — настоящая производная no t, ее мы используем при образовании и, а другое (превосходная дивергенция) войдет в S. К несчастью, справа в середине осталось еще одно слагаемое, ко­торое не является ни дивергенцией, ни производной по t. Так что пока еще не все закончено. После некоторых размышле­ний мы опять обращаемся к уравнениям Максвелла и, к счастью, обнаруживаем, что (СXE) равно —dB/dt.

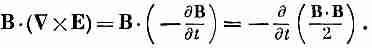
Это позволяет превратить дополнительный член в чистую производную чего-то по времени:

Вот теперь у вас получилось то, что нужно. Уравнение для энергии переписывается в виде

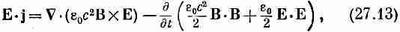
А это, если мы определим u и S как

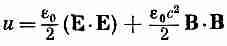
(27.14)

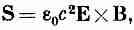
и

(27.15)

в точности напоминает уравнение (27.6). (Перестановкой со­множителей в векторном произведении мы добиваемся правиль­ного знака.)

Итак, наша программа успешно выполнена. Из выражения для плотности энергии мы видим, что она представляет сумму «электрической» и «магнитной» плотностей энергии, которые в точности равны выражениям, полученным нами в статике, когда мы находили выражение для энергии через поля. Кроме того, мы получили выражение для вектора потока энергии электромагнитного поля. Этот новый вектор S=e₀c²EXB по имени своего первооткрывателя называется «вектором Пойнтинга». Он говорит нам о скорости, с которой энергия движется в пространстве. Энергия, протекающая в секунду через малую поверхность da, равна S·nda, где n — вектор, перпендикуляр­ный к поверхности da. (Теперь, когда у нас есть формулы для u и S, можете, если хотите, забыть все выкладки.)

§ 4. Неопределенность энергии поля

Прежде чем заняться некоторыми приложениями формул Пойнтинга [т. е. выражений (27.14) и (27.15)], я хотел бы заме­тить, что на самом деле мы их не «доказали». Все, что мы сде­лали,— это нашли только возможное u и возможное S. Но откуда же нам известно, что, покрутив формулами, мы не придем к дру­гому выражению для u и другому выражению для S? Новое S и новое и будут отличаться от старых, но по-прежнему будут удовлетворять уравнению (27.6). Такое вполне может случиться. Однако в формулы, которые получаются при этом, всегда входят различные производные полей (причем это всегда члены второго порядка типа второй производной или квадрата первой произ­водной). Для u и S можно фактически написать бесконечное число различных выражений, и до сих пор никто не думал над экспериментальной проверкой того, которое же из них истинное. Люди полагают, что простейшее выражение, по-видимому, и должно быть истинным, но надо сознаться, что мы так и не знаем, как же на самом деле распределена энергия в электромагнитном поле. Пойдем по тому же легчайшему пути и постулируем, что энергия поля определяется выражением (27.14). При этом вектор потока S должен задаваться уравнением (27.15).

Самое интересное то, что единого способа избавиться от неопределенности энергии поля, по-видимому, вообще нет. Иног­да утверждают, что эту проблему можно разрешить, используя теорию гравитации; при этом приводятся такие доводы. В теории гравитации источником гравитационного притяжения является вся энергия. Поэтому если нам известно, какие гравитационные силы действуют на свет, то можно правильно определить плот­ность энергии электричества. До сих пор, однако, такими тон­кими экспериментами, которые позволили бы точно определить гравитационное влияние на электромагнитное поле, никто не занимался. Впрочем, установлено, что свет при прохождении около Солнца отклоняется, поэтому мы можем говорить, что Солнце притягивает к себе свет. Во всяком случае, найденные нами выражения для электромагнитной энергии и потока всегда всеми признавались. И хотя иногда результаты, полученные с их использованием, казались странными, никто никогда не обна­ружил в них чего-то невероятного, какого-то расхождения с экспериментом. Согласимся со всеми и будем считать, что, по-видимому, здесь все в порядке.

Мне хотелось бы сделать еще одно замечание о формуле для энергий. Прежде всего формула для энергии поля в единице объема очень проста — это сумма электрической и магнитной энергий, если электрическую энергию мы определим как Е², а магнитную — как В². Эти выражения были найдены нами как возможные выражения для энергии при рассмотрении статиче­ских задач. Кроме него, мы нашли для энергии электростати­ческого поля и несколько других выражений, например j, которое в электростатическом случае равно интегралу от Е·Е. Однако в электродинамическом случае это равенство нарушает­ся, и нет критерия, позволяющего установить, которая из фор­мул правильна. Но теперь мы это знаем. Аналогично, мы нашли выражение для магнитной энергии, которое верно в самом общем случае.

§ 5. Примеры потоков энергии

Наша формула для вектора потока энергии S представляет нечто новое. Теперь следует посмотреть, насколько она годится в некоторых специальных случаях, а также проверить ее на том, что мы знали раньше. Первым нашим примером будет свет. В световой волне векторы Е и В направлены под прямым углом друг к другу и направлению распространения волны (фиг. 27.2). В электромагнитной волне величина В равна (1/с)Е, а поскольку они направлены под прямым углом, то величина (ЕXE) равна просто Е²/с. Таким образом, для света поток энергии в секунду через единичную поверхность равен

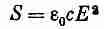
(27.16)

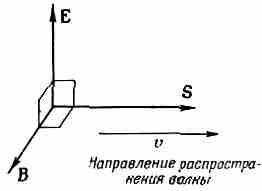
Фиг. 27.2. Векторы Е, В и S световой волны.

В световой волне, где E=E₀cosw(t-х/с), средняя скорость потока энергии через единичную площадь <S>_ср, которая на­зывается «интенсивностью» света, равна среднему значению электрического поля, помноженному на e_ас:

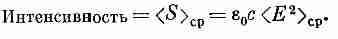
(27.17)

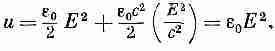
Этот результат, как ни странно, мы уже получали в гл. 31, § 5 (вып. 3), когда изучали свет. Мы получили его совсем другим путем и поэтому можем сейчас в него поверить. Когда у нас есть пучок света, то плотность энергии в пространстве задается урав­нением (27.14). Воспользовавшись теперь тем, что в световой волне сВ=Е, получаем

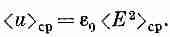
Однако вектор Е изменяется в пространстве, поэтому средняя плотность энергии равна

(27.18)

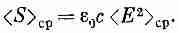
Далее, свет распространяется со скоростью с, поэтому можно думать, что энергия, проходящая в секунду через квадратный метр, равна произведению с на количество энергии в кубическом метре, т. е.

Все в порядке. Мы снова получили выражение (27.17).

Возьмем теперь другой пример, на этот раз очень любопыт­ный. Рассмотрим поток энергии в медленно заряжающемся кон­денсаторе. (Мы не хотим сейчас иметь дело со столь высокими ча­стотами, при которых конденсатор становится похожим на резо­нансную полость, но нам не нужен и постоянный ток.) Возьмем обычный конденсатор с круглыми параллельными пластинами (фиг. 27.3). Между ними создается почти однородное электри­ческое поле, которое изменяется с течением времени. Полная электромагнитная энергия внутри конденсатора в любой момент равна произведению плотности энергии и на объем. Если радиус пластин равен а, а расстояние между ними h, то полная энергия, заключенная между пластинами, будет

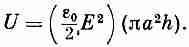
(27.19)

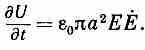
С изменением напряженности Е эта энергия тоже меняется. Когда конденсатор заряжается, внутренний объем приобретает энергию со скоростью

(27.20)

Так что должен существовать поток энергии, направленный откуда-то со стороны внутрь объема. Вы, конечно, думаете, что он идет от проводов, заряжающих конденсатор,— а вот и нет! Поток внутрь никоим образом не может идти с этой стороны, так как Е перпендикулярно к пластинам, а поэтому ЕXВ должно быть параллельно им.

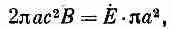
Вы, вероятно, помните, что при зарядке конденсатора воз­никает магнитное поле, которое направлено по окружности вокруг оси. Об этом говорилось в гл. 23. Воспользовавшись последним уравнением Максвелла, мы там нашли, что магнитное поле на краю конденсатора определяется выражением

или

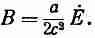
Направление его показано на фиг. 27.3. Таким образом, на краях конденсатора, как видно из рисунка, возникает поток энергии, пропорциональный ЕXВ. Так что энергия на самом деле втекает в конденсатор не со стороны проводов, а со стороны окружаю­щего его пространства.

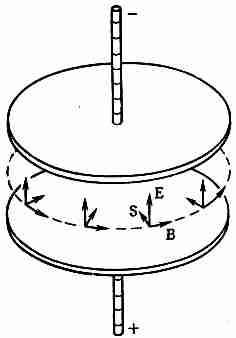
Фиг. 27.3. Вблизи заряженного конденсатора вектор Пойнтинга S направлен внутрь него

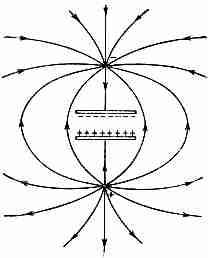
Фиг. 27.4. Поле вне конденсатора, заряженного двумя очень удален­ными зарядами.

Давайте проверим, согласуется ли полный поток через всю поверхность между краями пластин со скоростью изменения внутренней энергии. Для этого лучше всего повторить весь путь, проделанный нами при выводе выражения (27.15). Посмотрим, к чему он приведет. Площадь поверхности равна 2pah, а абсолютная величина S=e₀c²(EXB) равна

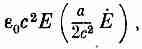
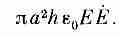
так что полный поток энергии будет

Это совпадает с уравнением (27.20). Удивительная вещь! Ока­зывается, при зарядке конденсатора энергия идет туда не через провода, а через зазор между краями пластин. Вот что говорит нам эта теория!

Как это может быть? Вопрос не из легких, но вот вам один из способов рассуждения. Предположим, у нас есть заряды, расположенные над и под конденсатором вдали от него. Когда такие заряды расположены вдалеке, то конденсатор окружает хотя и слабое, но необычайно протяженное поле (фиг. 27.4). Затем, когда заряды подходят все ближе и ближе, поле стано­вится все сильнее и сильнее и все теснее «обнимает» конденсатор. Так что энергия поля, которая вначале была далеко, движется «по направлению» к конденсатору и в конце концов входит в про­странство между пластинами.

В качестве следующего примера давайте посмотрим, что происходит с кусочком провода (с ненулевым сопротивлением), по которому течет ток. Поскольку провод обладает каким-то сопротивлением, то вдоль него действует электрическое поле, которое порождает ток, а в результате падения потенциала вдоль провода существует также параллельное его поверхности электрическое поле вне провода (фиг. 27.5). Кроме того, наличие тока порождает также магнитное поле, направленное по окружности вокруг провода.

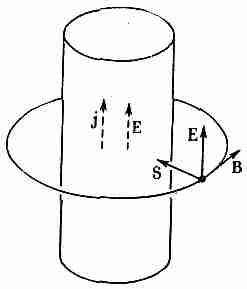
Фиг. 27.5. Вектор Пойнтинга S вблизи провода с током.

Векторы Е и В направлены под прямым углом, а поэтому вектор Пойнтинга направлен радиально, как это показано на рисунке. Внутрь проводника со всех сторон втекает энергия. Она, разумеется, должна быть равна энергии, теряемой проводником в виде тепла.

Таким образом, наша «сумасшедшая» теория говорит, что электроны получают свою энергию, растрачиваемую ими на создание теплоты извне, от потока энергии внешнего поля внутрь провода. Интуиция нам подсказывает, что электрон пополняет свою энергию за счет «давления», которое толкает его вдоль провода, так что энергия как будто должна течь вниз (или вверх) по проводу. А вот теория утверждает, что на самом деле на электрон действует электрическое поле, создаваемое очень да­лекими зарядами, и электроны теряют свою энергию, расходуе­мую на тепло именно из этих полей. Энергия отдаленных заря­дов каким-то образом растекается по большой области простран­ства и затем втекает внутрь провода.

Наконец, чтобы окончательно убедить вас в том, что это явно ненормальная теория, возьмем еще один пример, когда электрический заряд и магнит покоятся — сидят себе рядышком и не шевелятся. Представьте, что мы взяли точечный заряд, по­коящийся вблизи центра магнитного бруска (фиг. 27.6). Все находится в покое, так что энергия тоже не изменяется со вре­менем; Е и В постоянны. Но вектор Пойнтинга утверждает, что здесь есть поток энергии, так как ЕXВ не равно нулю. Если вы понаблюдаете за потоком энергии, то убедитесь, что он циркули­рует вокруг этой системы. Но никакого изменения энергии не происходит; все, что втекает в любой объем, снова вытекает из него.

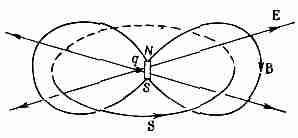
Фиг. 27.6. Заряд и магнит дают вектор Пойнтинга. циркулирую­щий по замкнутой петле.

Это напоминает круговой поток несжимаемой воды. Итак, в такой, казалось бы, статической ситуации есть поток энергии. Выглядит, прямо скажем, абсурдно!

А, может быть, это все-таки не так уж удивительно, если вспомнить, что так называемый «статический» магнит представ­ляет на самом деле непрерывно циркулирующий ток. Внутри постоянного магнита электроны все время крутятся. Так что, может быть, циркуляция энергии не так уж удивительна.

У вас, без сомнения, начинает создаваться впечатление, что теория Пойнтинга, по крайней мере частично, опровергает вашу интуицию относительно того, где находится энергия электро­магнитного поля. Вам может показаться, что необходимо за­няться «починкой» своей интуиции, отработкой ее на множестве примеров. Однако в этом, по-видимому, никакой необходимости нет. Не думаю, чтобы вы оказались в большом затруднении, забыв на время, что энергия втекает внутрь провода извне, а не течет вдоль него. Не так уж важно, используя идею сохра­нения энергии, указать во всех деталях, какой путь избирает энергия. Циркуляция энергии вокруг магнита и заряда в боль­шинстве случаев, по-видимому, совершенно несущественна. Хотя это и не так уж важно, однако ясно, что повседневная интуиция нас обманывает.

§ 6. Импульс поля

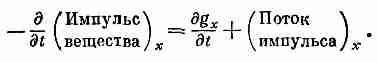
Теперь мне бы хотелось поговорить об импульсе поля. Поле обладает энергией; точно так же в единице объема оно обладает каким-то импульсом. Обозначим плотность импульса через g. Импульс, разумеется, может иметь различные направления, по­этому g должно быть вектором. Временно мы будем говорить об одной компоненте и для начала возьмем x-компоненту. По­скольку любая компонента импульса сохраняется, то мы можем сразу написать закон примерно такого вида:

Левая часть тривиальна. Скорость изменения импульса веще­ства равна просто действующей на него силе. Для частиц F=q(E+vXB), а для распределенных зарядов на единицу объема действует сила F=(rE+jXB). Однако слагаемое «поток импульса» несколько странно. Оно не может быть дивергенцией какого-то вектора, ибо это не скаляр, а скорее x-компонента некоторого вектора. Но как бы то ни было оно должно иметь вид

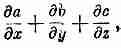
поскольку x-компонента импульса должна течь в каком-либо из трех направлений. Во всяком случае, каковы бы ни были а, b и с, такая комбинация предполагается равной потоку x-ком­поненты импульса.

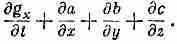
Дальше по правилам той же самой игры напишем rЕ+jXB только через Е и В, исключив плотность заряда r и плотность тока j и затем жонглируя слагаемыми и произведя подстановку, получаем

Сопоставляя затем разные слагаемые, мы должны найти выра­жения для g_x, a, b и с. В общем, здесь масса работы, но мы не собираемся заниматься ею. Вместо этого мы найдем только выражение для плотности импульса g и притом совсем другим способом.

В механике есть очень важная теорема, которая говорит: каков бы ни был поток энергии любого вида (энергия поля или какой-то другой сорт энергии), произведение ее количества, прошедшего через единицу площади в единицу времени, на 1/с² равно импульсу в единице объема пространства. В случае электродинамики эта теорема говорит, что g равно вектору Пойнтинга, поделенному на с²:

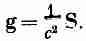
(27.21)

Так что вектор Пойнтинга дает нам не только поток энергии, но после деления на с² и плотность импульса. Этот же результат получился бы из анализа, который мы только что предполагали проделать, однако более заманчиво воспользоваться общей теоремой. Сейчас мы рассмотрим несколько интересных приме­ров и рассуждений, призванных убедить вас в справедливости этой общей теоремы.

Первый пример: возьмем множество заключенных в ящик частиц. Пусть, скажем, их будет Nштук на кубический метр, и пусть они движутся вдоль ящика со скоростью v. Рассмотрим теперь воображаемую плоскость, перпендикулярную к v. Поток энергии через единицу площади этой плоскости в секунду равен Nv (т. е. числу частиц, пересекающих плоскость за се­кунду), умноженному на энергию каждой частицы. Энергия же каждой частицы будет m₀c²/Ц(l-v²/c²). Так что поток энергии равен

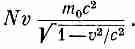
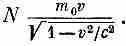
Но импульс каждой частицы равен m₀vЦ(1-v²/c²), откуда плотность импульса будет

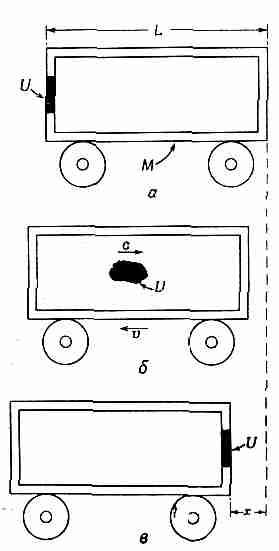
Фиг. 27.7. Порция энергии U, двигаясь со скоростью с, несет импульс, равный U/c.

что в полном согласии с теоремой как раз равно 1/с² на поток энер­гии. Таким образом, для пучка частиц теорема оказывается вер­ной.

Верна она и для света. При изучении света (см. вып. 3) мы установили, что, когда происхо­дит поглощение света, поглоти­телю передается некоторое коли­чество импульса. Действительно, в гл. 34 (вып. 3) мы видели, что импульс равен поглощенной энер­гии, деленной на с [уравнение (34.24)]. Пусть U₀будет энергией, падающей в секунду на единичную площадь, тогда переданный той же поверхности за то же время импульс равен U₀/c. Но импульс распространяется со скоростью с, так что его плотность перед поглотителем должна быть равна U₀/с². Теорема снова справедлива.

Наконец, я приведу рассуждение Эйнштейна, которое еще раз продемонстрирует то же самое утверждение. Предположим, у нас есть вагон с какой-то большой массой М, который может без трения катиться по рельсам. В одном его конце расположено устройство, способное «выстреливать» какие-то частицы или световой импульс (совершенно безразлично, чем оно стреляет), которые ударяются о противоположный конец вагона. Следо­вательно, некоторое количество энергии, скажем U, находив­шееся первоначально на одном конце (фиг. 27.7,а), перелетает на противоположный конец (фиг. 27.7,в). Таким образом, энергия U перемещается на расстояние, равное длине вагона L. Этой энергии U соответствует масса U/с², так что если вагон вначале стоял, то его центр масс должен передвинуться. Эйнштейну не понравилось заключение о том, что центр масс предмета можно переместить какими-то манипуляциями внутри него. Он считал, что никакие внутренние действия не могут изменить центр масс. Но если это так, то при перемещении энергии U с одного конца на другой сам вагон должен откатиться на расстояние х

(фиг. 27.7,в). В самом деле, нетрудно убедиться, что полная масса вагона, умноженная на х, должна быть равна произведе­нию перемещенной энергии U/c²на длину L (при условии, что U/C²много меньше М), т. е.

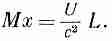
(27.22)

Теперь рассмотрим конкретный случай, когда энергия пере­носится вспышкой света. (Все рассуждения можно повторить и для частиц, но мы будем следовать за Эйнштейном, который интересовался проблемами света.) Что заставляет вагон дви­гаться? Эйнштейн рассуждал так: при испускании света должна быть отдача, какая-то неизвестная отдача с импульсом р. Именно она заставляет вагон откатиться назад. Скорость ва­гона v при такой отдаче должна быть равна импульсу отдачи, поделенному на массу М:

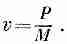
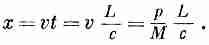
Вагон движется с этой скоростью до тех пор, пока свет не достигнет противоположного конца. Ударяясь, свет отдает импульс вагону и останавливает его. Если х мало, то время, в течение которого вагон движется, равно l/c, так что мы

Подставляя х в (27.22), находим

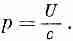
Снова получилось соотношение между энергией и импульсом света. Деля это на с, находим плотность импульса g=p/c, и опять

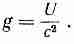
(27.23)

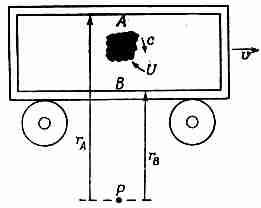
Вас может удивить, так ли уж важна теорема о центре масс. Может быть, она нарушается? Возможно, но тогда вы теряете и закон сохранения момента количества движения. Предполо­жим, что наш вагончик движется по рельсам с некоторой ско­ростью и, и мы «выстреливаем» какое-то количество световой энергии от потолка к полу, например из точки А в точку В (фиг. 27.8). Посмотрим теперь на момент количества движения относительно точки Р. До того как порция энергии U покинула точку А, у нее была масса m=U²/c и скорость v, так что ее мо­мент количества движения был равен mvr_a. Когда же она приле­тела в точку В, масса ее остается прежней, и если импульс всего вагона не изменился, то она по-прежнему должна иметь скорость v.

Фиг. 27.8. Для сохранения мо­мента количества движения отно­сительно точки Р порция энергии U должна нести импульс U/c.

Однако момент количества движения относительно точки Р будет уже mvr_B. Таким образом, если вагону при излу­чении света не передается никакого импульса, т. е. если свет не переносит импульса U/c, то момент количества движения должен измениться. Оказывается, что в теории относительности сохранение момента количества движения и теорема о центре масс тесно связаны между собой. И если неверна теорема, то нарушается и закон сохранения момента количества движения. Во всяком случае, общий закон должен быть справедлив и для электродинамики, так что им можно воспользоваться для полу­чения импульса поля.

Упомянем еще о двух примерах импульса в электромаг­нитном поле. В гл. 26, §2, мы говорили о нарушении закона дей­ствия и противодействия для двух заряженных частиц, движу­щихся перпендикулярно друг другу. Силы, действующие на эти частицы, не уравновешивают друг друга, так что действие и противодействие оказываются неравными, а полный импульс вещества поэтому должен изменяться. Он не сохраняется. Но в такой ситуации изменяется и импульс поля. Если вы рас­смотрите величину импульса, задаваемую вектором Пойнтинга, то она оказывается непостоянной. Однако изменение импульса частицы в точности компенсируется импульсом поля, так что полный импульс частиц и поля все же сохраняется.

Второй наш пример — система заряда и магнита, изобра­женная на фиг. 27.6. К своему огорчению, мы обнаружили, что в этом примере энергия «бегает по кругу», но, как нам теперь известно, поток энергии и импульса пропорциональны друг дру­гу, поэтому здесь мы имеем дело с циркуляцией импульса. Но циркуляция импульса означает наличие момента количества движения. Поле обладает моментом количества движения. Пом­ните парадокс с соленоидом и зарядами на диске, описанный в гл. 17, § 4? Казалось, что при включении тока весь диск должен начать крутиться.

Остается загадка, откуда возникает этот момент количества движения? Ответ на этот вопрос такой: если у вас есть магнитное поле и какие-то заряды, то поле имеет и момент количества движения. Он возник еще при создании самого поля. Когда же поле выключается, момент количества движения отдается обратно. Так что диск в этом парадоксе начнет крутиться. Таинственный циркулирующий поток энергии, который сна­чала кажется чем-то непонятным, на самом деле абсолютно необходим. Ведь существует реальный поток импульса. Он необходим для выполнения закона сохранения момента коли­чества движения в целом.