Глава 14 РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ (II)
Глава 14
РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ (II)
§1. Работа
§2. Движение при наложенных связях
§3. Консервативные силы
§4. Неконсервативные силы
§5. Потенциалы и поля
§ 1. Работа
В предыдущей главе мы ввели много новых понятий и идей, играющих важную роль в физике. Идеи эти столь важны, что, пожалуй, стоит посвятить целую главу внимательному ознакомлению с ними. Мы не будем здесь повторять «доказательства» и красивые приемы, позволяющие просто получать важные результаты, а вместо этого сосредоточим наше внимание на обсуждении самих идей.
Штудируя любой вопрос технического характера, для понимания которого нужна математика, мы всегда сталкиваемся с необходимостью понять и отложить в памяти массу фактов и идей, объединенных определенными связями, Существование этих связей можно «доказать или «показать». Ничего не стоит спутать само доказательство с тем соотношением, которое оно устанавливает. Конечно, куда важнее выучить и запомнить не доказательство, а само соотношение. Тогда уж в любом случае мы сможем сказать: «Легко показать, что...» то-то и то-то верно, а то и действительно показать это, Приводимые доказательства почти всегда состряпаны, сфабрикованы с таким расчетом чтобы, во-первых, их легко было воспроизвести мелом на доске или пером на бумаге и, во-вторых, чтобы они выглядели поглаже. В итоге доказательство выглядит обманчиво просто, хотя, быть может, на самом деле автор много часов искал разные пути расчета, пока не нашел самый изящный — тот, который приводит к результату за кратчайшее время! Глядя на вывод формулы, надо вспоминать не этот вывод, а скорее сам факт, что то-то и то-то можно доказать. Конечно, если доказательство требует особых математических выкладок или «трюков», никогда прежде не виденных, то надо обратить внимание... впрочем, не на сами трюки, а на их идею.
Ни одно из доказательств, приведенных в этом курсе, автор не запомнил с тех времен, когда сам учил физику. Наоборот, он просто вспоминает, что то-то является верным, и, пытаясь пояснить, как это доказывается, сам придумывает доказательство в тот момент, когда оно необходимо. И всякий, кто действительно изучил предмет, должен быть в состоянии поступать так же, не запоминая доказательств. Вот почему в этой главе мы будем избегать вывода различных положений, сделанных ранее, а просто будем подводить итоги.
Первая идея, которую нужно будет переварить,— это то, что работа производится силой. Физический термин «работа» ничего общего не имеет с общежитейским ее смыслом...
Физическая работа выражается в виде ?F·ds, или «контурный интеграл от F по ds «скалярно»; последнее означает, что если сила направлена, скажем, в одну сторону, а тело, на которое сила действует, перемещается в другую сторону, то работу совершает только составляющая силы в направлении перемещения. Если бы, например, сила была постоянна, а смещение произошло на конечный отрезок Ds, то работа, выполненная постоянной силой на этом пути, была бы равна произведению составляющей силы вдоль Ds на Ds. Правило гласит: «работа есть сила на путь», но подразумевается лишь составляющая силы в направлении перемещения, умноженная на Ds, или, что одно и то же, составляющая перемещения в направлении силы, умноженная на F.
Очевидно, что сила, направленная под прямым углом к перемещению, никакой работы не произведет.
Если, далее, вектор смещения Ds разложить на составляющие, т. е. если истинное смещение есть Ds и мы хотим считать, что оно состоит из составляющих смещения Dx; в направлении х, Dy в направлении у и Dz в направлении z, то вся произведенная работа перемещения тела из одного места в другое может быть рассчитана по трем частям: отдельно работа смещения вдоль х, вдоль у и вдоль z. Работа перемещения вдоль х требует знания только соответствующей составляющей силы Fxи т. д., так что работа равна FxDx+FyDy+FzDz. Когда сила не постоянна, а движение запутанное, криволинейное, то нужно разбить путь на множество малых Ds, сложить работы переноса тела вдоль каждого Ds и перейти к пределу при Ds, стремящемся к нулю. В этом смысл понятия «контурный интеграл».
Все, что мы только что сказали, содержится в формуле W=?F·ds. Но одно дело назвать эту формулу прекрасной, и
совсем другое — понять ее смысл и ее следствия.
Смысл слова «работа» в физике настолько отличается от того, что подразумевают под этим словом в обычных обстоятельствах, что надо тщательно проследить это различие. Например, по точному смыслу физического определения работы, если вы держите в руках двухпудовую гирю, вы не совершаете никакой работы. Вас бросает в пот, ваши руки дрожат, вы дышите тяжело, как будто взбежали по лестнице, а работы вы не совершаете. Когда вы взбегаете по лестнице, то считается, что вы совершаете работу; когда вы сбегаете по лестнице вниз, то, согласно физике, мир производит работу над вами, а вот когда вы держите предмет, стоя неподвижно, никакой работы не производится. Физическое определение работы отличается от физиологического по причинам, которые мы сейчас кратко изложим.
Когда вы держите груз, вы, конечно, выполняете «физиологическую» работу. Отчего вас бросает в пот? Почему для такого занятия вам необходимо хорошо питаться? Почему все механизмы внутри вас работают в полную силу, когда вы подставили спину под груз? Ведь можно на этот груз не тратить никаких усилий, стоит лишь положить его на стол, и стол спокойно и мирно, не нуждаясь ни в какой энергии, будет держать себе тот же груз на той же высоте! Физиология дает примерно следующее объяснение. У человека и у других животных есть два рода мышц. Одни, называемые поперечнополосатыми, или скелетными, контролируются нашей волей; таковы, например, мышцы рук. Другие мышцы называются гладкими (например, мышцы внутренностей или у моллюсков большой замыкающий мускул, который закрывает створки). Гладкие мышцы работают очень медленно, но способны «оцепенеть»; это значит, что если, скажем, моллюску нужно удержать свои створки в определенном положении, то он их удержит, какая бы сила на них ни нажимала. Многие часы способен он без устали держать створки под нагрузкой, подобно столу, на который положен груз; мышца «застывает» в определенном положении, молекулы ее как бы схватываются друг с другом, не совершая никакой работы, не требуя от моллюска никаких усилий. Нам же нужны непрерывные усилия, чтобы удержать вес. Это объясняется просто устройством поперечнополосатых мышц. Когда нервный импульс достигает мышечного волокна, оно несколько сокращается и затем опять расслабляется; когда мы держим груз, то в мышцу сплошным и обильным потоком текут нервные импульсы, множество волокон сокращается, пока другие отдыхают. Это даже можно увидеть: когда рука устает держать тяжесть, она начинает дрожать. Происходит это потому, что поток импульсов нерегулярен и уставшие мышцы не успевают вовремя на них ответить. Почему же мышцы собраны по такой неудачной схеме? Неизвестно почему, но природа не сумела создать быстродействующих гладких мышц. А куда удобнее было бы поднимать грузы именно гладкими мышцами: они способны замирать на месте, они могут цепенеть и для этого не нужно было бы совершать никакой работы и не нужна никакая энергия. Правда, у этих мышц есть один недостаток: они очень медленно работают.
Но вернемся к физике и зададим еще один вопрос: зачем нам подсчитывать выполненную работу? Ответ: потому что это интересно и полезно. Потому что работа, которую производит над частицей равнодействующая всех приложенных к ней сил, в точности равна изменению кинетической энергии этой частицы. Если тело толкнуть, оно наберет скорость, и D(v2)=2/m(F·Ds).
§ 2. Движение при наложенных связях
Силы и работа обладают еще одним интересным свойством. Пусть имеется некоторый уклон, какая-то криволинейная колея, по которой частица должна двигаться без трения. Или имеется маятник — груз на ниточке; нить маятника вынуждает груз двигаться по кругу вокруг точки подвеса. Намотав нить на колышек, можно в качании менять точку подвеса, так что траектория груза будет складываться из двух окружностей разного радиуса. Все это примеры так называемых неподвижных связей без трения.
В движении с неподвижными связями без трения эти связи не производят никакой работы, потому что реакции связей всегда прилагаются к телу под прямым углом к самим связям; так обстоит дело и с реакцией колеи и с натяжением нити.
Силы, возникающие при движении частицы вниз по склону под действием тяжести, весьма и весьма запутаны: здесь и реакции связи, и сила тяжести, и т. п. И все же, если основывать свои расчеты движения лишь на сохранении энергии и на учете только силы тяжести, получается правильный результат. Это выглядит довольно странно, потому что это не совсем правильно; надо было бы пользоваться равнодействующей силой. Тем не менее работа, произведенная только силой тяжести, оказывается равной изменению кинетической энергии, потому что работа сил связей равна нулю (фиг. 14.1).
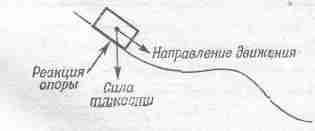
Фиг. 14.1. Силы, действующие на тело, скользящее без трения.
Важное свойство сил, о котором мы говорили, состоит в том, что если силу можно разбить на две или несколько «частей», то работа, выполняемая самой силой при движении по некоторой кривой, равна сумме работ, произведенных каждой «частью» силы. Если мы представляем силу в виде векторной суммы нескольких сил (силы тяжести, реакции связей и т. д., или x-составляющих всех сил плюс y-составляющие и т.д., или еще как-нибудь), то работа всей силы равна сумме работ тех частей, на которые мы ее разделили.
§ 3. Консервативные силы
В природе существуют силы, скажем сила тяжести, обладающие замечательным свойством — «консервативностью» (никаких политических идей, ничего двусмысленного в этом понятии нет). Когда мы подсчитываем, какую работу выполняет сила, двигая тело от одной точки к другой, то вообще работа зависит от траектории; но в особых случаях эта зависимость пропадает. Если работа не зависит от траектории, мы говорим, что сила консервативна. Иными словами, если интеграл от произведения силы на приращения смещений между точками 1 и 2 (фиг. 14.2) один раз вычислен вдоль кривой А, а другой — вдоль кривой В, и оба раза получается одинаковое количество джоулей, и если это выполнено для любой кривой, соединяющей эту пару точек, и если это же справедливо для любой пары точек, то говорят, что сила консервативна. В таких обстоятельствах интеграл работы между точками 1 и 2 можно легко подсчитать и дать для него формулу. А в других случаях это не так просто: нужно задавать еще форму кривой; но когда работа не зависит от кривой, то, ясное дело, остается только зависимость от положений точек 1 и 2.
Чтобы доказать это, рассмотрим фиг. 14.2.
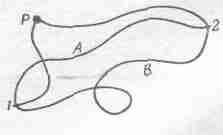
Фиг. 14.2. Возможные пути, соединяющие две точки в поле сил.
Фиксируем произвольную точку Р. Криволинейный интеграл работы на участке (1,2) можно вычислить, разбив его на две части: работу на участке (1, Р) и работу на участке (Р, 2), потому что сейчас у нас всюду консервативные силы, и по какому пути ни пойти, значение работы одно и то же. Работа перемещения из точки Р в любую точку пространства является функцией положения конечной точки. Она зависит и от Р, но мы во всем дальнейшем анализе точку Р закрепим, так что работа перемещения тела от точки Р к точке 2 будет некоторой функцией положения точки 2. Она зависит от того, где находится точка 2; если переместить тело в другую точку, ответ будет другой.
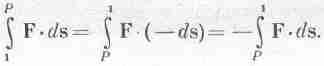
Обозначим эту функцию положения через -U(x, у, z); желая отметить, что речь идет именно о точке 2 с координатами x2, y2, z2, мы будем просто писать U(2), сокращая обозначение U(хг, у2, z2). Работу перемещения из точки 1 в точку Р можно написать, обратив направление интегрирования (переменив знаки всех ds). Другими словами, работа на участке (1,Р) равна работе на участке (P,1) со знаком минус:
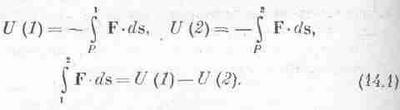
Значит, работа на участке (Р,1) есть -U(1), а на участке (Р,2) есть -U(2). Поэтому интеграл от 1 до 2 равен -U(2) плюс [-U1) назад], т. е. + U(1)-U(2):
Величина U(1)-U(2) называется изменением потенциальной энергии, a U можно назвать потенциальной энергией. Мы будем говорит, что когда предмет находится в положении 2, то он обладает потенциальной энергией U(2), а в положении 1 — потенциальной энергией U(1). Когда он находится в положении Р, его потенциальная энергия равна нулю. Если бы вместо Р взять любую другую точку Q, то оказалось бы (это предоставляется доказать вам самим), что потенциальная энергия всех точек изменилась бы только на постоянную добавку. Так как сохранение энергии зависит только от изменений ее, то эта добавочная постоянная никакого значения не имеет. Вот поэтому точка Р произвольна.
Итак, у нас имеются два утверждения: 1) работа, выполняемая силой, равна изменению кинетической энергии системы, но 2) математически для консервативных сил выполненная работа равна минус изменению функции U, называемой потенциальной энергией. Как следствие этих утверждений возникает еще одно: если действуют только консервативные силы, сумма потенциальной U и кинетической Т энергий остается постоянной:
T+U=const. (14.2)
Рассмотрим формулу потенциальной энергии для ряда случаев. Если поле тяготения однородно, если мы не поднимаемся до высот, сравнимых с радиусом Земли, то сила постоянна и направлена вертикально, а работа равна просто произведению силы на расстояние по вертикали. Стало быть,
U(z)=mgz, (14.3)
и за точку Р с нулевой потенциальной энергией можно принять любую точку на поверхности z=0. Но можно также говорить, что потенциальная энергия равна mg(z-6), если нам так уж этого хочется! Все результаты в нашем анализе останутся теми же, кроме того что потенциальная энергия на поверхности z=0 будет равна -mg6. Разницы никакой, ведь в расчет надо принимать только разности потенциальных энергий.
Энергия, необходимая для сжатия пружины на расстояние х от точки равновесия, равна
U(x)=1/2kx2 (14.4)
и нуль потенциальной энергии приходится на точку х=0, т. е. на равновесное состояние пружины. И здесь тоже мы можем добавить любую константу.
Потенциальная энергия тяготения точечных масс Mи m на расстоянии rдруг от друга равна
U(r)=-GMm/r. (14.5)
Константа здесь выбрана так, чтобы потенциал исчезал на бесконечности. Конечно, эту же формулу можно применить и к электрическим зарядам, поскольку закон один и тот же:
U(r)=q1q2/4pe0r. (14.6)
Давайте теперь поработаем с одной из этих формул, посмотрим, поняли ли мы их смысл.
Вопрос: С какой скоростью должна отправиться ракета с Земли, чтобы покинуть ее?
Ответ: Сумма кинетической и потенциальной энергий должна быть постоянной; покинуть Землю — значит удалиться от нее на миллионы километров; если у ракеты только-только хватает сил, чтобы покинуть Землю, то надо предположить, что там, вдалеке, ее скорость будет равна нулю и что на бесконечности она будет едва-едва двигаться. Пусть а — радиус Земли, а M— ее масса. Кинетическая плюс потенциальная энергии первоначально были равны l/2 mv2 -GmM/a. В конце движения эти обе энергии должны сравняться. Кинетическую энергию в конце движения мы считаем нулевой, потому что тело еле движется (почти с нулевой скоростью), а потенциальная энергия равна величине GmM, деленной на бесконечность, т. е. опять нулевая. Значит, с одной стороны стоит разность двух нулей; поэтому квадрат скорости должен быть равен 2GM/a. Но GM/a2 это как раз то, что называют ускорением силы тяжести g. Итак,
v2=2ga.
С какой скоростью должен двигаться искусственный спутник, чтобы не падать на Землю? Мы когда-то решали эту задачу и получили v2=GM/a. Значит, чтобы покинуть Землю, нужна скорость, в Ц2 большая, чем скорость вращения спутника вокруг Земли. Иными словами, чтобы улететь с Земли, нужно вдвое больше энергии (энергия пропорциональна квадрату скорости), чем чтобы облететь вокруг нее. Поэтому исторически сначала были совершены облеты искусственных спутников вокруг Земли, для чего понадобились скорости около 7,8 км/сек. И только потом космические корабли были заброшены в мировое пространство; для этого потребовалось уже вдвое больше энергии, т. е. скорости около 11,2 км/сек.
Продолжим теперь наш обзор характеристик потенциальной энергии. Давайте рассмотрим взаимодействие двух молекул или двух атомов, например двух атомов кислорода. Когда они находятся далеко друг от друга, они притягиваются с силой, обратно пропорциональной седьмой степени расстояния, а при тесном сближении они сильно отталкиваются. Проинтегрировав минус седьмую степень расстояния, чтобы получить работу, мы увидим, что потенциальная энергия U (функция расстояния между атомами кислорода) изменяется как минус шестая степень расстояния (на больших расстояниях).
Если мы чертим некую кривую потенциальной энергии U(r) (фиг. 14.3), то при больших r она выглядит как r-6, а при достаточно малых r достигает минимума.
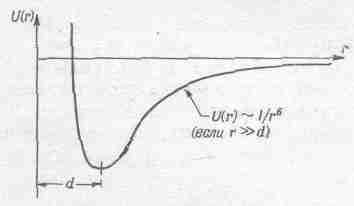
Фиг. 14.3. Потенциальная энергия взаимодействия двух атомов как функция расстояния между ними.
Минимум потенциальной энергии в точке r=d означает, что если мы сдвинемся от нее на малое расстояние, на очень малое расстояние, то произведенная работа, равная изменению потенциальной энергии на этом промежутке, почти равна нулю, потому что на донышке кривой энергия почти не меняется. Значит, в этой точке сила равна нулю, и это есть точка равновесия. Условие равновесия можно высказать и иначе: для удаления из точки равновесия в любую сторону нужно затратить работу. Когда два атома кислорода расположены так, что никакой энергии из их силы взаимодействия больше выжать нельзя, то они находятся в наинизшем энергетическом состоянии и промежуток между ними равен d. Так выглядит молекула кислорода, когда она не нагрета. При нагревании атомы колеблются и расходятся; их можно и совсем развести, но для этого нужно определенное количество работы или энергии, равное разности потенциальных энергий в точках r=d и r=Ґ. При попытке сблизить атомы энергия быстро возрастает вследствие их взаимного отталкивания.
Почему мы говорим о потенциальной энергии? Потому что идея силы не очень пригодна для квантовой механики, там более естественна идея энергии. Когда мы рассматриваем более сложные взаимодействия: ядерного вещества, молекул и т. д., то, хотя понятия силы и скорости «рассасываются» и исчезают, оказывается, что понятие энергии все же остается. Поэтому в книгах по квантовой механике мы находим кривые потенциальной энергии, но очень редко увидим график силы взаимодействия двух молекул, потому что те, кто изучает эти явления, больше уже привыкли думать об энергии, чем о силе.
Заметим еще, что, когда на тело одновременно действуют несколько консервативных сил, потенциальная энергия тела есть сумма потенциальных энергий от каждой силы. Это то, что мы утверждали и раньше, потому что, когда сила представляется векторной суммой сил, работа, производимая ею, равна сумме работ, производимых отдельными силами; поэтому ее можно представить как изменения потенциальных энергий от каждой силы по отдельности. Значит, общая потенциальная энергия равна сумме всех частей.
Мы можем обобщить это на случай системы многих тел, как, например, Юпитера, Сатурна, Урана и т. д. или атомов кислорода, азота, углерода и т. д., взаимодействующих друг с другом попарно, причем силы взаимодействия каждой пары консервативны. В таких условиях кинетическая энергия всей системы есть просто сумма кинетических энергий всех отдельных атомов, или планет, или частиц, а потенциальная энергия системы есть сумма потенциальных энергий взаимодействия отдельных пар, рассчитанных в предположении, что других частиц нет. (На самом деле для молекулярных сил это неверно, и формула получается несколько сложнее; для ньютонова тяготения это определенно справедливо, а для молекулярных сил годится лишь как приближение. Можно, конечно, говорить о потенциальной энергии молекулярных сил, но она иногда оказывается более сложной функцией положений атомов, чем простая сумма попарных взаимодействий.) Поэтому потенциальная энергия в частном случае тяготения представляется суммой по всем парам i и j членов — Gmimj/rij [как было показано в уравнении (13.14)]. Уравнение (13.14) выражает математически следующее предложение: общая потенциальная плюс общая кинетическая энергии не меняются со временем. Пусть себе различные планеты вращаются, обращаются и покачиваются, все равно если подсчитать общую потенциальную и общую кинетическую энергии, то окажется, что их сумма всегда остается постоянной.
§ 4. Неконсервативные силы
Мы потратили немало времени, обсуждая свойства консервативных сил. Что же мы теперь скажем о неконсервативных силах? Мы хотим разобраться в этом вопросе более подробно, чем это обыкновенно делают, и показать, что неконсервативных сил не бывает! Оказывается, все основные силы природы, по-видимому, консервативны. Не подумайте, что это следствие из законов Ньютона. На самом деле, насколько представлял себе это сам Ньютон, силы могут быть неконсервативными, как, например, трение, которое кажется неконсервативным. Употребляя слово «кажется», мы проводим современную точку зрения, которая доказывает, что все глубинные силы, все силы взаимодействия между частицами на самом фундаментальном уровне суть силы консервативные.
Когда мы, например, анализируем систему наподобие большого шарового звездного скопления (фотографию такого скопления мы показывали) с тысячами взаимодействующих звезд, то формула для общей потенциальной энергии состоит просто из суммы слагаемых, каждое из которых выражает взаимодействие какой-то пары звезд; точно так же и кинетическая энергия есть сумма кинетических энергий всех отдельных звезд. Но шаровое скопление как целое движется и в пространстве, и окажись мы от него так далеко, что не смогли бы различать отдельных деталей, мы бы приняли его за единый предмет. Если бы при этом к нему были приложены какие-то силы, то часть из них могла бы двигать его как целое и мы бы увидели, как центр этого тела движется. С другой стороны, прочие силы могли бы, если так можно выразиться, «тратиться» на повышение потенциальной или кинетической энергии «частиц» внутри «тела». Положим, например, что действие этих сил привело бы к расширению всего скопления и увеличению скоростей «частиц». Общая энергия «тела» на самом деле сохранялась бы. Но, глядя издалека нашими слабыми глазами, не различающими беспорядочных внутренних движений, мы бы видели только кинетическую энергию всего тела и нам бы казалось, что энергия не сохраняется, хотя все дело было бы в том, что мы не различаем деталей. Оказывается, что это всегда так: общая энергия Вселенной, кинетическая плюс потенциальная, если как следует посмотреть, всегда постоянна.
Изучая тончайшие свойства вещества на атомном уровне, не всегда легко разделить общую энергию на две части, потенциальную и кинетическую, и не всегда такое разделение необходимо. Во всяком случае, оно возможно почти всегда, так что давайте говорить, что оно всегда возможно и что потенциальная плюс кинетическая энергии мира постоянны. Итак, общая потенциальная плюс кинетическая энергии внутри целого мира постоянны, и если «мир» — это изолированный кусок вещества, то энергия его постоянна, если только нет внешних сил. Но, как мы видели, часть кинетической и потенциальной энергий предмета может быть внутренней (например, внутренние молекулярные движения), внутренней в том смысле, что мы ее не замечаем. Мы знаем, что в стакане воды все колеблется, все части беспрерывно движутся, так что внутри имеется определенная кинетическая энергия, на которую мы обычно никакого внимания не обращаем. Мы не замечаем движения атомов, рождающего теплоту, и поэтому не называем его кинетической энергией, но основа тепла — все-таки кинетическая энергия. Точно так же и внутренняя потенциальная энергия может, например, иметь форму химической энергии: когда мы сжигаем бензин, выделяется энергия, потому что потенциальные энергии атомов при новом их размещении оказываются ниже, чем при прежнем расположении. Строго говоря, теплоту нельзя считать чисто кинетической энергией, в нее входит и часть потенциальной энергии; то же относится и к химической энергии, так что лучше объединить их и говорить, что общая кинетическая и потенциальная энергии внутри тела — это частично тепло, частично химическая энергия и т. д. Во всяком случае, все эти различные формы внутренней энергии иногда рассматривают как «потерянную» энергию в том смысле, как сказано выше; когда мы изучим термодинамику, нам все это станет яснее.
В качестве другого примера возьмем трение. Неверно, что кинетическая энергия в результате трения исчезает; это неверно, хотя скользящее тело и впрямь останавливается и кажется, что кинетическая энергия пропала. Но она не пропадает, ибо атомы внутри тела начинают двигаться с большим запасом кинетической энергии; хоть мы этого и не можем увидеть, но можно догадаться об этом по повышению температуры. Конечно, если не обращать внимания на тепловую энергию, то теорема о сохранении энергии покажется неправильной.
Еще в одном случае может показаться, что энергия не сохраняется: когда мы изучаем часть всей системы. Вполне естественно, что если что-то взаимодействует с чем-то внешним и мы пренебрегаем этим взаимодействием, то теорема о сохранении энергии будет выглядеть неверной.
В классической физике в потенциальную энергию включались только тяготение и электричество, но теперь у нас есть и атомная энергия и многое другое. В классической теории, например, свет — это особая форма энергии, но можно, если нам этого хочется, представить себе энергию света как кинетическую энергию фотонов, и тогда наша формула (14.2) опять окажется справедливой.
§ 5. Потенциалы и поля
Теперь обратимся к некоторым идеям, связанным с потенциальной энергией и с понятием поля. Пусть два больших тела А и В притягивают к себе третье малое тело с суммарной силой F. Мы уже отмечали в гл. 12, что сила притяжения частицы может быть представлена как произведение ее массы mна вектор С, зависящий лишь от положения частицы:
F = mC.
Тяготение можно анализировать, считая, что в каждом месте пространства имеется вектор С, который «действует» на массу, помещенную в это место, но который присутствует там безотносительно к тому, поместили ли мы туда массу или нет. Вектор С имеет три составляющие, и каждая из них является функцией от (х, y, z) — функцией положения в пространстве. Такую вещь мы называем полем и говорим, что тела А и В создают поле, т. е. «делают» вектор С. Когда тело помещено в поле, то сила действия на это тело равна его массе, умноженной на величину вектора поля в той точке, куда тело попало.
С потенциальной энергией можно сделать то же самое. Так как потенциальная энергия, интеграл от (Сила)·(ds), может быть записана в виде массы m, умноженной на интеграл от (Поле)·(ds) — это простое изменение масштаба, — то потенциальную энергию U(x, у, z) тела, расположенного в точке (х, у, z), можно записать как произведение mна другую функцию. Назовем ее потенциалом y.. Интеграл ?C·ds равен
-y, подобно тому как ?F·ds=-U; они отличаются только
масштабом:
U= -?F·ds=-m?C·ds=my. (14.7)
Зная в каждой точке пространства эту функцию y (х, y, z), можно немедленно вычислить потенциальную энергию тела в любой точке, а именно U(x, у, z) — my (х, у, z). Теперь, как видите, это стало делом пустяковым. Но на самом деле это отнюдь не пустяк, потому что иногда намного приятнее описать поле, задав распределение потенциала во всем пространстве, чем задавать С. Вместо трех сложных компонент векторной функции проще задать скалярную функцию y. Кроме того, когда поле создается многими массами, величину y рассчитывать легче, чем три компоненты С: потенциалы—скаляры, их можно просто складывать, не заботясь о направлениях сил. А поле С, как мы сейчас увидим, легко восстановить, зная y. Пусть у нас есть точечные массы m1, m2,... в точках 1, 2..., и мы хотим знать потенциал yв некоторой произвольной точке Р. Тогда он оказывается простой суммой потенциалов отдельных масс в точке Р:
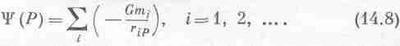
Этой формулой, представляющей потенциал в виде суммы потенциалов отдельных масс, мы пользовались в предыдущей главе, чтобы вычислить потенциал сферического слоя (мы тогда сложили потенциалы всех поясков, на какие был нарезан слой). Итог расчета показан на фиг. 14.4.
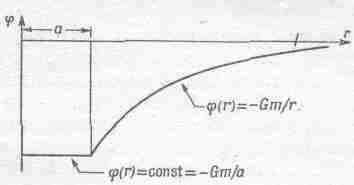
Фиг. 14.4. Потенциал тяготеющего сферического слоя радиусом а.
Потенциал отрицателен, равен нулю на бесконечности, падает как 1/r, пока r не станет равным а, и затем внутри слоя становится постоянным. Вне слоя потенциал равен —Gm/r (т— масса слоя), что полностью совпадает с потенциалом точки с массой т, помещенной в центре сферического слоя. Но такое совпадение существует только для точек снаружи слоя, а во внутренних точках потенциал оказывается равным —Gm/a и больше не меняется! А когда потенциал постоянен, то поля нет: если потенциальная энергия не меняется, то сила отсутствует, потому что, когда мы двигаем тело из одной внутренней точки в другую, работа, выполняемая силой, в точности равна нулю. Почему? Да потому, что работа передвижения тела из одной точки в другую равна минус изменению потенциальной энергии (или соответствующий интеграл от поля равен изменению потенциала). Но потенциальная энергия в обеих точках одинакова, значит, ее изменение равно нулю, и поэтому никакой работы при любых движениях внутри сферического слоя не производится. А это возможно лишь тогда, когда внутри слоя нет никаких сил.
В этих рассуждениях кроется ключ к вычислению силы или напряженности поля, когда потенциальная энергия известна.
Пусть потенциальная энергия тела в точке (х, у, z) дана, а мы хотим узнать, какая сила действует на него в этой точке. Для этого нужно знать потенциал не только в этой точке, но и в соседних. Почему? Попробуем вычислить x-компоненту силы (если мы это сумеем сделать, то точно таким же способом мы вычислим и у- и z-компоненты, определив тем самым всю силу). Если б мы сдвинули тело на малое расстояние Dx, то работа, произведенная силой над телом, равнялась бы x-компоненте силы, умноженной на Dx (если Dx достаточно мало), и должна была бы быть равна изменению потенциальной энергии при переходе от одной точки к другой:
DW=-DU=FxDx. (14.9)
Мы просто применили формулу ?F·ds=-DU для очень
малых расстояний. Теперь разделим на Dx и обнаружим, что сила равна
Fx=-DU/Dx. (14.10)
Конечно, это не совсем точно. На самом деле нам нужно перейти в (14.10) к пределу при Dx, стремящемся к нулю, потому что (14.10) точно соблюдается только для бесконечно малых Dx. Мы узнаем в правой части (14.10) производную U по х и хотим написать -dUldx. Но U зависит и от х, и от у, и от z, и для такого случая математики придумали другое обозначение, которое рассчитано на то, чтобы напоминать нам, что надо быть очень осторожным, дифференцируя такую функцию. Этот символ напоминает, что только х считается изменяющимся, а у и z — нет. Вместо d они просто пишут «6 навыворот», или д. (По-моему, когда начинаешь изучать дифференциальные исчисления, то вообще лучше работать с д, а не с d; d всегда хочется сократить, а вот на д как-то рука не поднимается!) Итак, они пишут dU/dx, а иногда в припадке строгости, желая быть очень бдительными, они ставят за дх скобку с маленькими у, z внизу (dU/dx)yz, что означает: «Продифференцируй U по х, считая у и z постоянными». Но мы чаще всего не будем отмечать, что осталось постоянным, из контекста это всегда можно понять. Но зато всегда будем писать д вместо d как предупреждение о том, что эта производная берется при постоянных значениях прочих переменных. Ее называют частной производной, т. е. производной, для вычисления которой меняют часть переменных, х.
Итак, мы обнаруживаем, что сила в направлении х равна минус частной производной U по х:
Fx=-дU/дx (14.11)
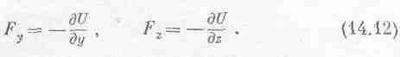
Точно так же и сила в направлении у получается дифференцированием U по у при постоянных х и z, а третья составляющая силы опять-таки есть производная по z при х и у постоянных:
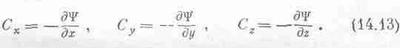
В этом и состоит способ получать силу из потенциальной энергии. Поле получается из потенциала в точности так же:
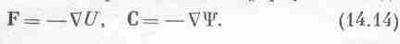
Заметим, кстати, что существует и другое обозначение (впрочем, пока оно нам не понадобится). Так как С есть вектор с компонентами х, у, z, то символы д/дх, д/ду, d/dz, дающие х-, у-, z-компоненты поля, чем-то напоминают векторы. Математики изобрели знаменитый символ С, или grad, называемый «градиентом»; это не величина, а оператор, он делает из скаляра вектор. У него есть три составляющие: x-компонента этого grad есть д/дх, y-компонента — д/ду, а z-компонента— d/dz, и мы можем позабавиться, переписав наши формулы в виде
Глядя на С; мы мгновенно узнаем, что наши уравнения векторные; но на самом деле уравнение (14.14) означает в точности то же, что и (14.11) и (14.12); просто это другой способ записи. Не желая писать каждый раз три уравнения, мы пишем одно лишь СU.
Еще один пример полей и потенциалов связан с электричеством. В этом случае сила, действующая на неподвижное тело, равна заряду, умноженному на поле: F = qЕ. (В x-составляющую силы входят, вообще говоря, и члены, которые зависят от магнитного поля. Но из уравнения (12.10) легко увидеть, что сила, действующая на частицу со стороны магнитных полей, всегда направлена поперек поля и поперек ее скорости. Благодаря этому свойству магнетизм не производит никакой работы над движущимся зарядом, потому что сила перпендикулярна перемещению. Значит, вычисляя кинетическую энергию в электрическом и магнитном полях, можно пренебречь вкладом магнитного поля, так как оно не изменяет кинетической энергии.) Положим, что имеется только электрическое поле. Тогда мы можем рассчитать энергию или произведенную работу точно таким же способом, как и для тяготения: вычислить величину j, равную минус интегралу от Е·ds от произвольной фиксированной точки Р до точки, в которой вычисляется потенциал; тогда потенциальная энергия в электрическом поле равна просто произведению заряда на эту величину j:
j(r) = -E·ds,
U=qj.
В качестве примера рассмотрим две параллельные металлические пластины с поверхностным зарядом ±s (на единицу площади) каждая. Такая штука называется плоским конденсатором. Мы уж убедились раньше, что снаружи пластин сила равна нулю, а между ними существует постоянное электрическое поле. Оно направлено от плюса к минусу и равно s/e0 (фиг. 14.5).

Фиг. 14.5. Поле между параллельными пластинами.
Мы хотим знать, какую работу надо совершить, чтобы перенести заряд от одной пластины к другой. Работа равна интегралу от (Сила.)·(ds). Его можно записать как произведение заряда на значение потенциала на пластине 1 минус та же величина на пластине 2:
W=?F·ds= q(j1-j2).
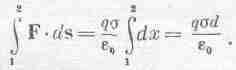
Интеграл здесь легко вычислить, так как сила постоянна, и если обозначить толщину конденсатора d, то интеграл равен
Разница в потенциалах Dj= sd/e0называется напряжением и j измеряют в вольтах. Когда мы говорим, что пара пластин заряжена до определенного напряжения, мы хотим этим сказать, что разность электрических потенциалов двух пластин равна стольким-то вольтам. У конденсатора, сделанного из двух параллельных пластин с поверхностным зарядом ±s, напряжение (или разность потенциалов этой пары пластин) равно sd/e0.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
Глава 27 ЭНЕРГИЯ ПОЛЯ И ЕГО ИМПУЛЬС
Глава 27 ЭНЕРГИЯ ПОЛЯ И ЕГО ИМПУЛЬС § 1. Локальные законы сохранения § 2. Сохранение энергии и электромагнитное поле§ 3. Плотность энергии и поток энергии в электромагнитном поле § 4. Неопределенность энергии поля § 5. Примеры потоков энергии§ 6. Импульс поля§ 1. Локальные
Глава 8 ЭЛЕКТРОСТАТИЧЕСКАЯ ЭНЕРГИЯ
Глава 8 ЭЛЕКТРОСТАТИЧЕСКАЯ ЭНЕРГИЯ §1.Электростатическая энергия зарядов. Однородный шар§2.Энергия конденсатора. Силы, действующие на заряженные проводники§З.Электростатическая энергия ионного кристалла§4.Электростатическая энергия ядра§5.Энергия в
ЭНЕРГИЯ ИЗ СРЕДЫ — ВЕТРЯК И СОЛНЕЧНЫЙ ДВИГАТЕЛЬ — ДВИЖУЩАЯ ЭНЕРГИЯ ИЗ ЗЕМНОГО ТЕПЛА — ЭЛЕКТРИЧЕСТВО ИЗ ЕСТЕСТВЕННЫХ ИСТОЧНИКОВ
ЭНЕРГИЯ ИЗ СРЕДЫ — ВЕТРЯК И СОЛНЕЧНЫЙ ДВИГАТЕЛЬ — ДВИЖУЩАЯ ЭНЕРГИЯ ИЗ ЗЕМНОГО ТЕПЛА — ЭЛЕКТРИЧЕСТВО ИЗ ЕСТЕСТВЕННЫХ ИСТОЧНИКОВ Есть множество веществ помимо топлива, которые возможно смогли бы давать энергию. Огромное количество энергии заключено, например, в
Глава 2. Энергия
Глава 2. Энергия Сохранение массы При рассмотрении импульса мы имели дело с тремя величинами: скоростью, массой и их произведением, т. е. самим импульсом.С точки зрения сохранения мы рассмотрели две из них: импульс, который сохраняется, и скорость, которая не сохраняется.
Глава шестая РАБОТА ИЗМЕНЯЕТ МАССУ
Глава шестая РАБОТА ИЗМЕНЯЕТ МАССУ Масса Допустим, что мы хотим заставить двигаться с определенной скоростью какое-нибудь покоящееся тело. Для этого мы должны приложить к нему силу. Тогда, если движению не препятствуют посторонние силы, вроде силы трения, тело придет в
Глава 11 Энергия и другие сохраняющиеся величины в ОТО
Глава 11 Энергия и другие сохраняющиеся величины в ОТО Я физик и имею право на сохранение энергии. Хуго Штейнхаус Развитие представлений о законах сохранения Идея сохранения появилась еще в Древней Греции в виде догадки о наличии неизменных субстанций в мире, где все
РАБОТА С ТЯЖЕЛОЙ ВОДОЙ
РАБОТА С ТЯЖЕЛОЙ ВОДОЙ 8.55. В предыдущих главах уже упоминалось о преимуществах тяжелой воды в качестве замедлителя. Тяжелая вода лучше, чем графит, замедляет нейтроны и меньше, чем графит, их поглощает. Поэтому возможно построить аггрегат цепной реакции с тяжелой водой и
Глава XII. Работа над атомной бомбой
Глава XII. Работа над атомной бомбой ПЛАН ГЛАВЫ 12.1. Общая цель работы, описанной в предыдущих главах — исследовать возможность создания атомных бомб и производства концентрированных, способных испытывать деление материалов, требующихся для таких бомб. В настоящей главе
РАБОТА ЛАБОРАТОРИИ
РАБОТА ЛАБОРАТОРИИ ВВЕДЕНИЕ12.23. Весь научный персонал в Лос-Аламосе был разделен на 7 отделов, которые потом в разное время реорганизовывались. Весной 1945 года существовали следующие отделы:1. теоретической физики, под руководством Г. Бете;2. экспериментальной ядерной
РАБОТА КОТЛА
РАБОТА КОТЛА Для пуска котла все кадмиевые полосы, кроме одной, удалялись. Оставшаяся полоса медленно выдвигалась наружу. По мере приближения к критическим условиям, интенсивность нейтронов внутри котла быстро возрастала. Следует, однако, заметить, что когда последняя
Глава 2. Е — это энергия
Глава 2. Е — это энергия Слово «энергия» на удивление молодо, проследить происхождение нынешнего его смысла удается лишь до середины 1800 годов. И дело вовсе не в том, что до той поры никто не осознавал, что вокруг нас существуют самые разные силы — потрескивание
Работа
Работа Если толкать или тянуть тело, не встречая при этом никакой помехи, то результатом будет ускорение тела. Происшедшее при этом приращение кинетической энергии называют работой силы A: По закону Ньютона ускорение тела, а следовательно, и прирост кинетической энергии
Сила и потенциальная энергия при колебании
Сила и потенциальная энергия при колебании При всяком колебании около положения равновесия на тело действует сила, «желающая» возвратить тело в положение равновесия. Когда точка удаляется от положения равновесия, сила замедляет движение, когда точка приближается к
ГРАНДИОЗНАЯ РАБОТА
ГРАНДИОЗНАЯ РАБОТА Хотя в их изначальные планы входило выделить оба элемента, после многих усилий им пришлось оставить полоний и заняться только радием. На основе предыдущих экспериментов супруги Кюри пришли к выводу о том, что его химические свойства проще, так что его