Глава 7 Наблюдательные подтверждения ОТО

Глава 7

Наблюдательные подтверждения ОТО

Эксперимент – истинный посредник между человеком и природой.

Леонардо да Винчи

Решение Шварцшильда

Для того чтобы обсудить многие эффекты ОТО, необходимо познакомиться с одним из самых важных решений (а возможно, и самым важным) уравнений ОТО – решением немецкого астронома Карла Шварцшильда (1873–1916). Оно получено в 1916 году, всего лишь через несколько месяцев после публикации Эйнштейном своих уравнений гравитационного поля. Это решение соответствует статическому сферически симметричному вакуумному пространству-времени. (О вакуумных решениях уравнений Эйнштейна см. Дополнение 4.) Слова, выделенные курсивом – это условия (ограничения), при которых искалось решение. Эти же условия определяют, чему в реальности должно соответствовать найденное решение – это пространство-время вокруг изолированного сферически симметричного тела. «Изолированного» – это в идеале, а в реальности – вокруг тела, достаточно удаленного от всех остальных тел. Таким образом, в очень хорошем приближении это решение описывает и гравитационное поле вокруг Солнца и каждой из планет Солнечной системы, шаровых звездных скоплений. Поэтому с использованием именно этого решения были проверены первые эффекты ОТО.

Решение Шварцшильда в математическом плане простое, поэтому мы немного с ним повозимся. Собственно, решением уравнений явилась метрика:

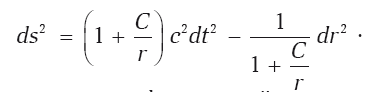
Здесь также в силу сферической симметрии мы опустили угловую часть, оставив только временную и радиальную. C – постоянная интегрирования, без дополнительных предположений или принципов ее определить невозможно. Здесь самое время обратиться к принципу соответствия. При «бесконечном» удалении от центра r ? ? эта метрика обращается в метрику пространства Минковского в сферических координатах, точно так же, как и метрика пространства-времени Ньютона, которую мы уже обсуждали. Значит, на достаточном удалении нам необходимо сравнить новую метрику с метрикой пространства-времени Ньютона, обсуждавшейся в предыдущей главе. При аккуратной процедуре приближения оказывается, что здесь основное возмущение в метрику плоского мира вносится только первым слагаемым в выражении для интервала. Нужно сравнить его с аналогичным членом в метрике Ньютона. Это нам даст C = –2GM/c², после чего метрика Шварцшильда запишется в окончательном виде:

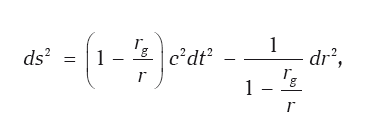
где величина r_g = 2GM/c² называется гравитационным радиусом. Мы так подробно обсуждаем решение Шварцшильда потому, что это еще и базовое решения для черных дыр, речь о которых впереди. Также потом мы обсудим смысл гравитационного радиуса. А сейчас важно отметить, что появился параметр, определяющий решение, – это масса тела M, обращение в нуль этого параметра превращает решение Шварцшильда в метрику плоского мира.