ПРОТИВ ТЕЧЕНИЯ

We use cookies. Read the Privacy and Cookie Policy

ПРОТИВ ТЕЧЕНИЯ

Общая теория относительности была создана А. Эйнштейном на основе минимального числа опытных данных о тяготении, с гениальной интуицией отобранных им. На протяжении многих десятилетий, прошедших с тех пор, все предсказания этой теории, которые можно было проверить, неизменно подтверждались.

Были обнаружены и затем тщательно измерены маленькие поправки в движениях планет Солнечной системы, предсказываемые теорией. В 1919 году А. Эддингтон во время полного солнечного затмения обнаружил искривление световых лучей в поле тяготения Солнца, предсказанное А. Эйнштейном.

Затем было обнаружено покраснение световых лучей, выходящих из повышенного поля тяготения, что также предсказывалось теорией.

Наконец, в 70-е годы с большой степенью уверенности были открыты черные дыры, эти удивительные образования, не похожие ни на что из уже известного в природе. Здесь общая теория относительности выступает не в качестве малых поправок к уже известным процессам, а проявляется во всей полноте, кардинально меняя геометрию пространства и свойства времени.

За все эти годы не было обнаружено ни одного факта, который заставил бы усомниться в теории относительности. Все это, вместе взятое, весь опыт истории науки XX века заставляет относиться весьма серьезно и к другим предсказаниям теории, которые еще не нашли прямого экспериментального или астрофизического подтверждения.

Мы видели, что современная физика, описывающая глубинное строение материи, развивается в направлении, начатом А. Эйнштейном. Выясняется, что природа всех физических взаимодействий едина. Весьма вероятно, что в основе свойств физической материи лежат сложные геометрические особенности пространства-времени.

В этой главе мы расскажем о новых возможностях, предсказываемых теорией. Эти возможности более чем фантастичны. Но такова стремительная современная наука, сводящая почти до нуля путь от фантастики до реальности! Правда, читатель может скептически пожать плечами: «Все, о чем будет говориться, — это пока лишь утверждения, основанные на рядах формул на листках бумаги, исписанных теоретиками. До каких-либо зримых воплощений в практику здесь еще очень далеко!»

И он, безусловно, будет прав. Теория — это еще не практика. Л. Больцман как-то в шутку сказал: «Один из моих друзей определил практика как человека, ничего не понимающего в теории, а теоретика — как мечтателя, вообще не понимающего ничего».

И все же хочется еще раз напомнить, что в XX веке стали практикой такие удивительные открытия, как, например, ядерная энергия или возможность космических полетов. О подтверждении предсказаний общей теории относительности уже говорилось. Будем помнить мудрое изречение, что ничего нет более практичного, чем правильная теория.

Вот почему мы здесь расскажем о смелых мечтаниях теоретиков, об их наиболее дерзких идеях. Как сказал знаменитый английский физик, открывший электрон, Дж. Дж. Томсон: «Из всех услуг, которые могут быть оказаны науке, введение новых идей — самая важная».

Речь пойдет о возможности путешествия в прошлое.

Летом 1988 года я получил от К. Торна копию направленной в журнал «Физикэл ревью леттерз» работы, выполненной им вместе с молодыми его учениками М. Моррисом и У. Юртсевером. В статье приводились теоретические аргументы в пользу принципиальной осуществимости перемещений из будущего в прошлое. Это была смелая работа.

В науке и философии давно укоренилось мнение, что путешествие в прошлое невозможно. Напомним читателю, что возможность путешествия в будущее давно доказана. В разделе «Машина времени» мы уже рассматривали пример машины, позволяющей переместиться в далекое будущее. Это ракета, могущая двигаться с достаточно большой скоростью в космическом пространстве. После полета на ней космонавт, вернувшийся на Землю, оказывается в будущих эпохах истории нашей планеты.

Путешествие в будущее, конечно, непривычно для нас. Например, если космонавт проживет в ракете тридцать лет, а на Земле пройдет полтора века, то он окажется моложе своих праправнуков. Но все же это не ведет к каким-то видимым противоречиям. И жители Земли, и космонавты перемещались из прошлого в будущее во времени, как это всегда имеет место и в привычных для нас условиях. Только перемещение это происходило с разной скоростью — у космонавта много медленнее, чем у жителей Земли.

Иное дело — путешествие в прошлое. В случае такого перемещения можно было бы влиять на события, которые давно свершились. А раз так, то можно было бы менять и наше настоящее, которое зависит от изменяемых в прошлом событий. Хотя подобные истории давно встречаются на страницах фантастических романов, но реальную возможность этого никто из физиков до сих пор серьезно не обсуждал.

После опубликования статьи американских специалистов в научном журнале осенью 1988 года газета «Нью-Йорк таймс» писала: «Если бы удалось показать возможность путешествия в прошлое хотя бы в теории, это само по себе имело бы фундаментальные философские и научные последствия. Поскольку путешественник во времени, возможно, был бы способен теоретически менять ход событий в прошлом, включая свое собственное рождение, законы причинности, на которых основывается наука, были бы повергнуты в хаос».

Далее говорилось, что авторы сенсационного исследования отметают подобные гипотезы и один из них заявил, что они занимаются теоретической физикой, а не философией.

Последнее замечание абсолютно справедливо — сначала надо выявить саму возможность построения машины времени для путешествия в прошлое и только потом посмотреть, к каким следствиям это ведет.

Короткие сообщения о работе американских физиков промелькнули и в наших газетах, и в телевизионных передачах.

Здесь мы снова возвращаемся к машине времени, прообраз которой описан в фантастической повести Г. Уэллса, носящей то же название. Это была первая фантастическая повесть английского писателя, опубликованная в 1895 году и сразу сделавшая его знаменитым.

Сам процесс перемещения во времени в этой повести представляется как своего рода просматривание ускоренно прокручиваемой кинокартины. Путешественник по времени, неподвижно сидящий в кресле машины времени, видит быстро мелькающие «кадры» стремительно развивающихся событий, движущихся вперед при перемещении от прошлого к будущему или движущихся вспять при перемещении в обратном направлении. Этот «полет» в будущее или прошлое великолепно описан Г. Уэллсом. Вспомним, что в то время, когда создавалась повесть, кино только-только зарождалось.

В молодости писатель серьезно увлекался наукой, и это нашло отражение во всем его творчестве, в том числе и в первых произведениях.

Не менее впечатляющим, чем «полет» по времени, выглядит в повести и объяснение сути передвижения по времени, которое излагает герой в беседе с друзьями. Он начинает с очевидного замечания, что все предметы, имея три измерения — длину, ширину и высоту, — обязательно должны существовать хоть какой-то промежуток времени. Это и есть четвертое измерение, заключает герой. Он говорит: «В действительности же существует четыре измерения, из которых три мы называем измерениями пространства, а четвертое — временем существования… Единственное различие между временем и любым из трех пространственных измерений заключается в том, что наше сознание движется вдоль него».

Напомним, что эти строки были написаны за десять лет до создания специальной теории относительности. Далее герой Г. Уэллса утверждает, что разные изображения в нашем трехмерном пространстве помогают изучить четвертое измерение. «Например, вот портрет человека, когда ему было восемь лет, другой — когда ему было пятнадцать, третий — семнадцать, четвертый — двадцать три года и так далее. Все это, очевидно, трехмерные представления его четырехмерного существования, которое является вполне определенной и неизменной величиной в пространстве и времени».

Мы видим, что в этом описании история представляется как бы уже готовой, полностью записанной на ленту, как и у Лапласа. Вдоль этой записи можно скользить и вперед и назад. Герой повести говорит, что все дело в том, чтобы научиться скользить по времени вперед и назад так же легко, как мы это делаем в пространстве. Он подчеркивает, что и в пространстве мы не с одинаковой легкостью можем двигаться по всем направлениям. Так, совсем недавно человек не мог подниматься над поверхностью Земли на значительную высоту. Да и вообще он с гораздо большей легкостью двигается вниз, подчиняясь силе тяготения, чем вверх. Однако, говорит путешественник по времени, человек «вопреки силе тяготения может подняться вверх на воздушном шаре. Почему же ему не надеяться, что в конце концов он будет способен также остановить или ускорить свое движение по времени или даже направить свой путь в противоположную сторону?»

Конечно, повесть Г. Уэллса — это художественное произведение, посвященное социальным проблемам будущего и являющееся в какой-то степени, наверное, своеобразным предупреждением, демонстрирующим, как может деградировать человеческое общество, если будет разделено на антагонистические классы. Но он был великим художником, способным глубоко продумывать и научные детали, принципы, законы. Поэтому так ярко и запоминающе описаны им мечты о полетах во времени.

Не вернемся от этих мечтаний к науке второй половины XX века. Что можно с научной точки зрения сказать о возможности «полетов» в прошлое?

Прежде всего, сразу надо отметить, что представлять себе такое перемещение вспять по времени, как прокручивание кинокартины в обратном направлении «перед человеком, неподвижно сидящим в кресле», заведомо неверно. Мы увидим далее, что для перемещений по времени необходимо двигаться и в пространстве. Заметим также, что ни при каком «полете» по времени сами мы не может помолодеть. В каждом из нас, как и в любом другом человеке или какой-либо системе, время может течь только вперед, только от молодости к старости. Нам известен закон роста беспорядка, увеличения энтропии, а это и определяет старение организма. (Оговоримся здесь все же, что можно вообразить пока чисто фантастическую ситуацию, когда вмешательство извне в процессы в человеческом организме на уровне живой клетки может предотвратить старение и даже вернуть молодость, но это вопрос о регулировке жизненных процессов, а не о беге времени.) Направление «психологической стрелы времени», как мы знаем, совпадает с этой «термодинамической стрелой времени». Но можно представить, что человек с помощью специально сконструированной машины попадает в некий «тоннель», проходя который он движется вспять по отношению ко времени во внешнем пространстве и, выходя через другое отверстие этого «тоннеля», он попадает в прошлое. Сам путешественник в прошлое при этом, разумеется, вовсе не становится более молодым. Однако, попав в прошлое, он может, например, оказаться во времени своей юности или даже в эпохе до момента своего рождения!

Такое путешествие выглядит в некотором смысле как отделение небольшой части потока воды от могучей реки и перекачивание ее насосами по трубам вдоль берега в направлении противоположном основному потоку, а затем сбрасывание этой воды в реку далеко вверху по течению.

Нечто подобное такой картинке, только относящееся к реке времени, и рассматривается современной наукой как теоретическая возможность. Чтобы не рассердить слишком сильно моих коллег-физиков, которым кто-нибудь из читателей может рассказать, о чем я здесь написал, оговорюсь сразу, что некоторые из них (коллег) считают любое путешествие в прошлое решительно невозможным. Но к этим спорам мы еще вернемся.

Чистые теоретики, скорее даже математики, чем физики, уже давно в своих трудах рассматривали причудливые фантастические миры, в которых путешествие в прошлое возможно. Эти миры порождены решением систем уравнений общей теории относительности. По-видимому, все тогда считали, что эти решения не имеют ни малейшего отношения к действительности, хотя и интересны для исследования структуры самой теории. Тот факт, что формулы правильной теории могут давать неправильные — «физически бессмысленные» — результаты, знает, конечно, каждый из своего опыта знакомства со школьной арифметикой. Достаточно поставить в условие задачи неправильные числа, как «правильная» арифметика выдаст невероятный результат: скажем, чтобы вырыть котлован объемом 30 кубических метров за 4 дня при производительности труда равной 3 кубометрам на одного землекопа в день, необходимо… 2,5 землекопа. Подобные «ответы» доводили до слез не одного ребенка. Большинство физиков относило миры с причудливыми свойствами времени к подобным «ответам».

Специалисты все же терпеливо изучали курьезные решения уравнений теории, хотя полностью сознавали их нереальность. Ведь любопытно знать, как могут быть устроены такие вселенные, в которых имеются «петли времени» и можно оказаться в своем прошлом.

Одно из первых решений такого рода было получено К. Геделем в 1949 году. В нем рассматривалась стационарная неменяющаяся со временем Вселенная. Уже поэтому модель не могла отвечать действительности, ибо мы наблюдали разбегание галактик. Вселенная Геделя наполнена однородным веществом с довольно странными свойствами, и, самое важное — она вращается. В такой Вселенной расстояния между всеми частицами вещества неизменны. Если мы прикрепим к каждой частице совершенно одинаковые часы, то как бы мы ни сверяли их друг с другом, чтобы «одновременно» запустить для отсчета времени, это сделать не удастся: нет для этого вещества и связанных с ним часов понятия «одновременно».

В общем, получается весьма экзотическая модель фантастической Вселенной. В этой Вселенной есть, как принято говорить, «петли времени». Из любой ее точки можно отправиться по определенному пути так, что, идя с некоторой скоростью вперед и вперед, обходишь мир и возвращаешься в эту исходную точку точно в момент начала путешествия! Иначе говоря, путешественник огибает этот мир не только в пространстве, но и во времени.

Все это выглядело забавно. Словом, решение было настоящей для теоретиков математической игрушкой. Но и не более. Можно было относиться к существованию «петель времени» в решении К. Геделя как к смешному курьезу, подобному двум с половиной землекопам в рассмотренной выше арифметической задаче.

На решение Геделя обратил мое внимание А. Зельманов, когда я был еще студентом. Сам он использовал это решение как математический пример при доказательстве серьезной теоремы. Я же развлекался, исследуя забавные свойства кривых линий в этой Вселенной.

Теоретики «игрались» и с другими моделями, в которых есть «петли времени».

Одну из таких моделей мы с Я. Зельдовичем рассмотрели в нашей вполне серьезной (более семисот страниц) монографии «Строение и эволюция Вселенной». Эта модель очень поучительна, и я о ней здесь коротко расскажу, надеясь, что в результате вам станет чуть яснее, что имеется в виду, когда говорят о «петлях времени».

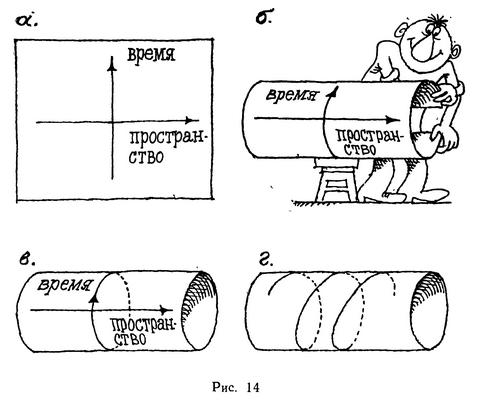
Мы уже изображали на картинках в этой книге пространство-время: по горизонтали откладывали пространственное направление, по вертикали — время. Поступим так и сейчас. Берем листок бумаги (на нем рисунок 14а), изгибаем его, как показано на рисунке 14б, и склеиваем верх рисунка с низом. Получается цилиндр (рисунок 14в), в котором окружности, его образующие, являются «петлями времени» (цилиндр следует считать бесконечно длинным). Скользя вместе с потоком времени по окружности цилиндра, возвращаемся к исходному моменту в прошлом. Можно, конечно, не возвращаться точно к исходному событию. Для этого достаточно перемещаться с течением времени вправо по пространству. Жизненный путь такого путешественника изобразится спиралью (рисунок 14г), она может быть все длиннее и длиннее «по времени» без постоянного кружения по одному и тому же временному пути, как это было при эволюции по «петле времени» на предыдущем рисунке.

Мы обсудили в нашей книге, вышедшей в 1975 году, что было бы с физическими процессами в такой замкнутой по времени Вселенной. При этом подчеркнули, что, несмотря на непривычность и известную «странность» процессов в этой модели мира, можно построить физику, в которой такая ситуация, возможно, не ведет к каким-либо противоречиям.

Все это были лишь короткие замечания о «петлях времени», но мы с Я. Зельдовичем относились к ним по-разному. Я — вполне серьезно и думал, что следует изучать возможность возникновения «петель времени» и в реальной Вселенной. Академику все это не очень нравилось с самого начала. Наша книга была затем переведена на английский язык и издана в Америке. Недавно я внимательно перечитал это место в английском варианте и обнаружил, что описание модели с «петлями времени» отсутствует в тексте! Я. Зельдовича, увы, уже нет в живых, и я не мог спросить, что произошло при переводе. Наверное, он при чтении корректуры выкинул это место, вызывавшее у него, по-видимому, антипатию.

К счастью, в другой книге, изданной мною на английском языке, описание модели с «петлями времени» имеется.

Должен, однако, заметить, что, теперь, уже к несчастью, я все же без должного внимания и серьезности отнесся к изучению возможности существования «петель времени». Отчасти это объясняется скептицизмом Я. Зельдовича, имевшим на меня огромное влияние. Я размышлял о «петлях времени» и до написания нашей книги, иногда возвращался к этим идеям и позже, кое-что пробовал вычислять, но все это делал без должной настойчивости. Только прочитав работу К. Торна и его учеников, я спохватился и буквально «загорелся» желанием хоть на шаг продвинуться к заветной цели — научиться «летать» в прошлое — и стал над этим работать. В чем же состояла суть предложений американских физиков?

Их работу можно разделить на два этапа. Первый состоял в рассмотрении возможности создания своеобразного «тоннеля», соединяющего два отверстия и подобного «горловинам», о которых мы уже говорили в разделе «Дыры в пространстве и времени». Только этот «тоннель» должен быть стабилен, чтобы сквозь него можно было ходить. Иными словами, эта часть работы состояла в доказательстве возможности застабилизировать «тоннель» от «схлопывания» силами тяготения и инерции.

Второй этап заключался в демонстрации того, как можно превратить этот «тоннель» с двумя входами в Машину Времени.

К. Торн вспоминает, что он занялся первой проблемой (как стабилизировать «тоннель») после ознакомления в 1985 году с рукописью романа К. Сагана «Контакт». Напомним, что К. Саган — известный астроном и не менее известный писатель. Он попросил К. Торна как специалиста проглядеть некоторые отрывки из своего нового фантастического романа, в котором решил использовать черные дыры для мгновенных перемещений героев к далеким звездам. Просьбу объяснил тем, что хотел бы как можно меньше вступать в своем романе в противоречие с выводами физики. К. Торну, проглядевшему роман по дороге в автомобиле, было ясно, что собственно черные дыры не годятся для каких-либо межзвездных путешествий. Из них нет выхода. А вот использовать «тоннели», соединяющие две дыры, если как-то застабилизировать и дыры и «тоннели», превратив их в статические конструкции, через которые можно проходить в любом направлении, вполне возможно. (Несколько сделанных им математических вычислений показали, что для стабилизации внутри «тоннеля» должно находиться необычное вещество или физическое поле, по свойствам схожее с вакуумноподобными состояниями (о нем мы говорили выше).

Затем он посоветовал К. Сагану переделать несколько мест в романе, что тот и сделал, переписав отдельные страницы уже в корректуре.

Но сам К. Торн не оставил этой идеи. Вместе со своим учеником М. Моррисом они принялись за работу, и в начале 1987 года первый вариант статьи, посвященной использованию (пока что гипотетическому) стабилизированных «тоннелей» для быстрых межзвездных путешествий, у них уже был готов.

В дальнейшем они вместе с Юртсевером описали более конкретное устройство «тоннеля». Что же необходимо для того, чтобы силы гравитации в столь необычной ситуации не вызвали схлопывания «тоннеля»?

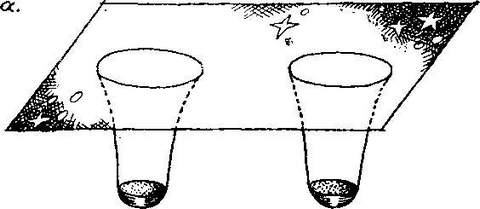
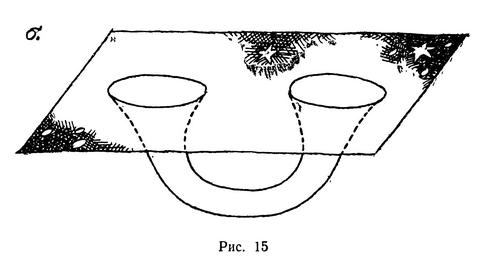
Они предлагают следующую конструкцию. Сначала в двух областях недалеко друг от друга создаются путем сжатия масс огромные гравитационные поля с сильным искривлением пространства в них (см. рисунок 15а). Затем эти области искривления соединяются в «тоннель» (рис. 15б). Возникший «тоннель», соединяющий два отверстия, аналогичен изображенному на рисунке 5а. Отличие от рисунка 5а заключается в том, что американцы предлагают в момент создания «тоннеля» застабилизировать его. Для этого в наиболее узком его месте надо поместить близко расположенные друг к другу две одинаково заряженные идеально проводящие ток пластинки. (В этом сильно искривленном пространстве каждая из пластин будет иметь сферическую форму.) Между пластинами возникнет специфическое вакуумноподобное состояние, называемое электромагнитным «казимировским вакуумом». Поясним на нескольких последующих страницах, что это такое.

О разных вакуумноподобных состояниях уже говорилось. До сих пор мы рассматривали их в необычных условиях больших плотностей и температур. Но оказывается, что особые вакуумноподобные состояния могут существовать и в нашей сегодняшней Вселенной.

Мы вынуждены сделать здесь небольшое отступление, с тем чтобы познакомиться с такими состояниями. Они очень важны во многих аспектах и представляют, конечно, самостоятельный интерес. Для нас же важно, что некоторые из них могут использоваться для стабилизации пространственных «тоннелей».

Прежде всего оказывается, что в нашей сегодняшней Вселенной могут существовать диковинные образования, являющиеся вкраплениями вакуумноподобных состояний или, как их иначе называют, вкраплениями «ложного вакуума» в наш «истинный вакуум».

Поясним, что здесь имеется в виду на упрощенном примере. Для этого вспомним, как образуется «наш вакуум», когда хиггсовское поле, являющееся ложным вакуумом, «скатывается» с потенциальной «горки». в «ложбину». Представим себе, что горка имеет вид холмика, возвышающегося над круглой ложбиной (см. рисунок 16). Теперь шарик, положенный на вершину, может скатиться в любое место круговой ложбинки. Это значит, что наинизшее энергетическое положение шарика может быть различным и характеризоваться точкой в ложбине. Эта точка может отмечаться направлением (стрелкой), по которому скатывался шарик с вершины. Таким образом, наинизшее энергетическое состояние должно характеризоваться еще и стрелкой. В разных точках пространства новый вакуум мог образовываться при «скатывании» шарика по разным направлениям, то есть «стрелка вакуума» может быть ориентирована по-разному, плавно поворачиваясь от места к месту.

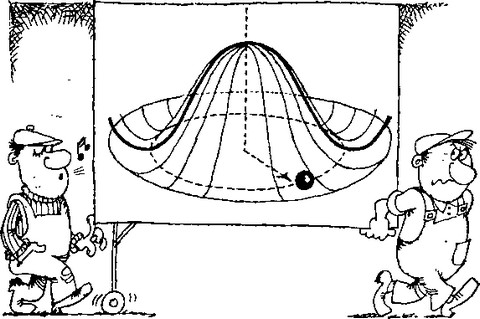
рис.16

Изобразим картину подобных стрелок в разных точках на плоскости. Может случиться так, что, плавно поворачиваясь от точки к точке, стрелки совершат полный поворот, как показано на рисунке 17. Тогда всегда найдется такая точка (точка А на рисунке 17), вблизи и вокруг которой стрелки имеют самые разные направления. Таким образом, в точке А нельзя придать стрелке такого направления, чтобы оно плавно переходило в направление стрелок в соседних точках. Это значит, что старое вакуумноподобное состояние («ложный вакуум») в данном месте не сможет «скатиться с горки» ни по какому направлению, чтобы вместе с другими стрелками образовать новый вакуум с плавным поворотом от точки к точке. В данной точке А останется старый вакуум, а вокруг будет вакуум новый!

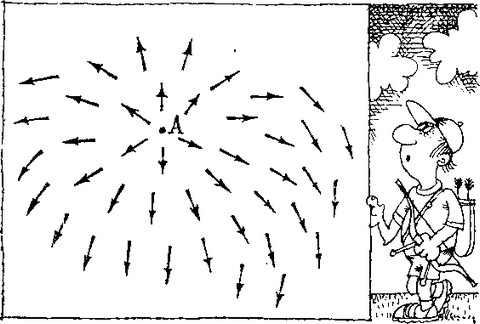
          рис.17

Интересную механическую аналогию возможности возникновения такой странной ситуации, когда система стремится перейти в более выгодное энергетическое состояние, но не всем точкам системы удается это сделать, придумал физик В. Унру.

Рассмотрим множество карандашей, стоящих вертикально на плоскости и соединенных между собой резинками, закрепленными у верхних концов (рисунок 18а). Ясно, что такое их положение неустойчиво, каждый из них при малейшем сотрясении стремится упасть. Но направление, в котором начнет падать каждый карандаш, случайно. Конечно, все они могут упасть примерно в одном направлении (рисунок 18б). Тогда вся система перейдет в более выгодное энергетическое состояние лежащих карандашей. Но представим себе, что далекие друг от друга карандаши начали падать в разные случайные стороны (рисунок 18в), увлекая за собой резинками соседние. Тогда возможно, что вокруг какого-либо карандаша (А на рисунке 18г) его соседи упадут по разным направлениям, натягивая за собой резинки. В результате карандаш А останется стоять, удерживаемый в таком положении растяжками-резинками. Теперь его положение вполне устойчиво и он не будет падать даже при заметных сотрясениях.

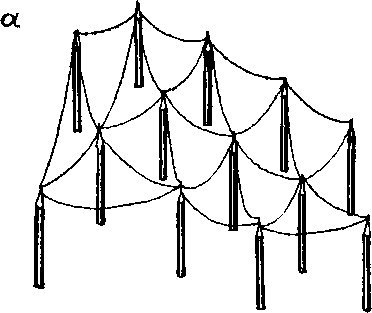
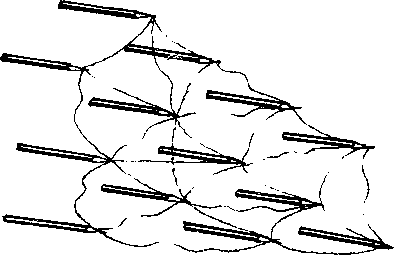
Рис. 18а, б

Так и в случае хиггсовского поля, образующего состояние ложного «вакуума». Оно может вокруг какой-то точки «скатиться» с горки в разных направлениях и тянуть за собой поле в данной точке, которое, как карандаш на растяжках-резинках, уже не может в этой точке «скатиться» с горки и останется в первоначальном положении.

Похожие ситуации могут возникать не только на плоскости, но и в пространстве. Такое, оказывается, возможно при спонтанном нарушении симметрии с понижением температуры образования нового вакуума, в который вкраплены точки старого вакуума и этот старый вакуум не может разрушиться, не может перейти в новый; по аналогии с тем, как карандаш А не может упасть и присоединиться к своим соседям.

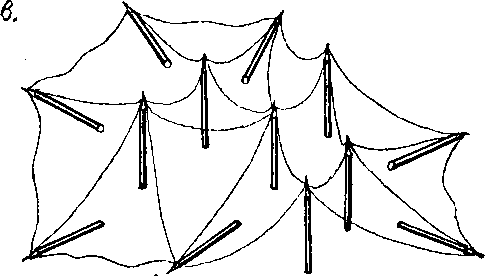
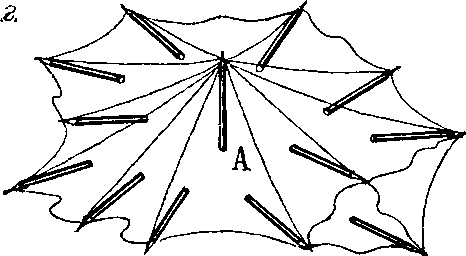
Рис. 18в, г

Необходимость возникновения таких удивительных объектов в теории великого объединения была показана советским физиком А. Поляковым и американским физиком Г. т’Хофтом в 1974 году. Что же это за образования?

Свойства их должны быть удивительны. Прежде всего, оказалось, что они должны быть изолированными магнитными полюсами.

Вспомним по этому поводу следующее весьма странное обстоятельство. Среди элементарных частиц есть электрически заряженные, но нет магнитозаряженных! Конечно, многие элементарные частицы обладают магнитными свойствами. Но при этом они представляют собой маленькие магнитики, то есть у них всегда есть и северный и южный магнитные полюса одновременно. Ни в мире элементарных частиц, ни вообще нигде в природе не обнаружен изолированный только, скажем, северный или только южный магнитный полюс. Они встречаются обязательно в паре. Если разрезать магнит пополам, то мы не получим, конечно, отдельно северный и отдельно южный полюса, а получим два магнита, и у каждого будет пара полюсов. В то же время изолированный электрический заряд — и положительный, и отрицательный — встречается сплошь и рядом. Почему это так? Чем магнитный заряд хуже электрического?

Да ничем! Еще в 1931 году английский физик П. Дирак показал, что изолированные магнитные заряды, как говорят — магнитные монополи, вполне могут существовать в природе. Физики уже давно пришли к твердому убеждению, что все то, что не запрещено специально законами природы, должно реально существовать (хотя иногда и является весьма редким или существующим в экзотических условиях).

Такова же судьба и предсказанного П. Дираком магнитного монополя. Он должен существовать, согласно теории Великого объединения, в виде вкраплений старого вакуума в новый. От этого образования исходят магнитные силовые линии точно так же, как из электрона исходят силовые линии электрического поля. Однако между магнитным монополем и электроном есть весьма существенные различия. Прежде всего, магнитный монополь очень массивен. Его масса должна быть, вероятно, в тысячу миллионов миллиардов раз больше массы протона. Даже с нашей макроскопической точки зрения это не так уж мало и составляет одну стомиллионную долю грамма.

Но наиболее существенное отличие монополя от истинно элементарных частиц состоит в том, что он обладает сложной внутренней структурой в пространстве. Большая часть его массы сосредоточена в очень маленьком объеме — в поперечнике в миллион миллиардов раз меньше размеров атомного ядра. Этот размер во столько же раз меньше размера протона, во сколько маленькая монетка меньше всей Солнечной системы!

Внутри этого крошечного объема сосредоточена большая энергия, там царит Великое объединение всех сил природы (кроме гравитации). Вокруг этого ядрышка есть зона, где присутствуют многочисленные X- и Y-бозоны. Во внешних, достаточно разреженных, областях имеются и W+-, W--, Z0 -бозоны. Внешние границы монополя имеют радиус примерно в сто раз меньше размеров атомного ядра. Читатель наверняка уже догадался, что огромная масса монополя является непреодолимым препятствием для получения его на ускорителях. Однако монополи могли остаться в виде реликтов процессов в очень ранней Вселенной. Как можно было бы их зарегистрировать?

Простейший путь состоит в следующем. Представим себе, что имеется круговая петля сверхпроводника, по которой течет электрический ток. Если магнитный монополь пролетит сквозь такое кольцо, то это приведет к появлению электродвижущей силы в кольце и ток в нем внезапно изменится, что может быть зарегистрировано. Разумеется, при этом должны быть приняты специальные меры защиты этого кольца от других причин, которые могут привести к внезапным изменениям тока в кольце.

Подобные эксперименты были проведены в начале 80-х годов в Стэнфордском университете (США) Б. Кабрерой. Он использовал в качестве проводника ниобиевое кольцо диаметром в пять сантиметров и охлажденное почти до температуры абсолютного нуля. В 1982 году он объявил, что после 150 дней наблюдений им зарегистрировано изменение тока в кольце, которое может быть вызвано пролетом монополя. Однако надежных подтверждений этого результата пока нет и вопрос остается открытым.

С другой стороны, мы знаем, что если монополи и есть в сегодняшней Вселенной, то их не может быть слишком много. В качестве детектора здесь опять выступают астрофизические наблюдения. Известно, что в нашей Галактике имеются крупномасштабные магнитные поля напряженностью около одной миллионной доли напряженности земного магнитного поля. Монополи должны двигаться под действием этих галактических полей, что приводит к уменьшению напряженности полей, подобно тому, как движение электрически заряженных частиц по проводнику от полюса к полюсу батареи вызывает уменьшение напряженности электрического поля. Так как мы надежно наблюдаем галактическое магнитное поле и знаем процессы, которые могут его генерировать, то можно подсчитать то максимально возможное количество монополей, которое могло бы быть во Вселенной, не вызывая еще очень быстрого уменьшения галактического магнитного поля. Оказывается, что в среднем во Вселенной на сто миллиардов миллиардов протонов может быть не больше одного магнитного монополя.

Наконец, монополь обладает еще одним свойством, представляющим незаурядный интерес. Как читатель помнит, внутри монополя, в его сердцевине, плотность энергии огромна и там в изобилии имеются переносчики сил Великого объединения. А эти переносчики могут превращать кварки в лептоны, в частности, вызывать распад протона, когда очень редко они рождаются в нем. Советский физик В. Рубаков в 1981 году обратил внимание на то, что встреча монополя с протоном может приводить к драматическим для протона последствиям. Частицы — переносчики сил Великого объединения внутри монополя могут взаимодействовать с кварками протона, вызывая его распад.

Так магнитный монополь может служить своеобразным катализатором распада протона. Сам он при этом не разрушается.

Описанные выше диковинки могут быть одним из типов «ложного вакуума», существующего в нашей Вселенной. Но в привычных нам условиях может существовать необычный вакуум и другого типа. Это «казимировский вакуум». Причем, если «реликтовый вакуум» — пока только гипотеза, «казимировский вакуум» реально наблюдался. Что это такое?

Необычное состояние было теоретически предсказано нидерландским физиком X. Казимиром, а его проявления экспериментально обнаружены в лаборатории фирмы «Филлипс Глуилампен фабрикен» в Эйндховене. «Казимировский вакуум» появляется между двух очень чистых, плоских, параллельно расположенных проводящих пластинок, когда их сближают на очень малые расстояния.

Виртуальные заряженные пары частиц непрерывно рождаются и аннигилируют в вакууме. Появляясь теперь между пластинками, они взаимодействуют с этими проводящими поверхностями. В результате вакуум между пластинками перестраивается, возникает отличная от нуля энергия (она оказывается отрицательной), и появляется также вакуумное натяжение между пластинками. Это и есть «казимировский вакуум». Он проявляет себя как слабое притяжение между пластинками. Его проявление зависит от степени сближения пластинок, их чистоты и так далее, и обычно оно очень слабо. Но теоретически «казимировский вакуум» можно сделать плотным, а вызываемые им натяжения — огромными.

Вот это необычное явление и предлагают в будущем использовать американские теоретики для стабилизации «тоннеля», соединяющего отверстия. Как мы помним, «казимировский вакуум» в их проекте возникает между двумя пластинами, введенными в «тоннель». Огромные специфические гравитационные силы, вызванные этим вакуумом, стабилизируют «тоннель». В пластинах делаются небольшие люки и изолирующая стенка так, чтобы сквозь пластины можно было проходить.

Надо подчеркнуть, что свойства материала, из которого должны быть сделаны заряженные пластины, столь необычны, что пока подходящее для этого вещество неизвестно в природе. Но, с другой стороны, нет и физических законов, которые запретили бы будущей высокоразвитой цивилизации создать такое вещество. То же можно сказать и о создании самого тоннеля. Пока не совсем ясны «детали» его строительства, хотя нет и каких-то специальных «запретов» природы на его создание.

Итак, предположим, что подобный «тоннель» в будущем будет построен. Тогда с отверстиями, которые он соединяет, можно провести следующую операцию. Их можно растащить на большое расстояние друг от друга, никак не меняя длины «тоннеля» между ними. На первый взгляд это выглядит совершенно невозможным. Но это только на первый взгляд.

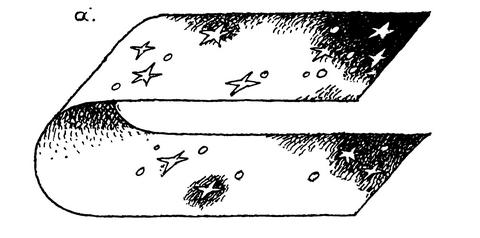
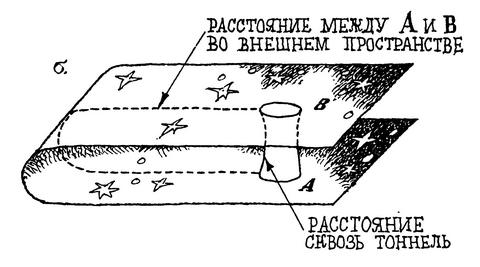
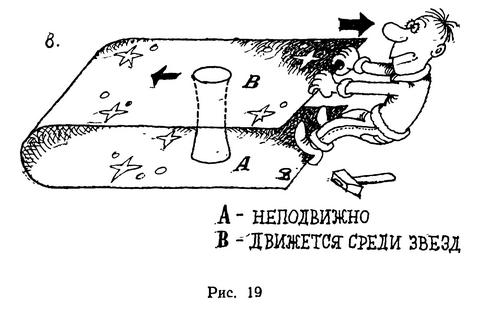
Представим себе опять для наглядности вместо нашего пространства пока без всяких отверстий и «тоннелей» плоский лист. Вообразим также плоские существа, которые могут передвигаться по этому «пространству» среди плоских звезд и могут проводить в нем геометрические измерения. Если теперь плавно изогнуть этот лист, как показано на рисунке 19а, не сминая его и не разрывая, то на листе ничто не изменится. Все геометрические соотношения сохранятся. Расстояния между любыми точками, если их измерять вдоль кратчайших линий, остающихся в пределах листа, не изменятся. Как говорят, внутренняя геометрия листа останется прежней. Но тогда плоские существа не могут знать, изогнут лист в каком-то внешнем пространстве или нет. Все будет на листе совершенно одинаково в обоих случаях. Теперь представим, что при изогнутом листе два отверстия соединены коротким «тоннелем» (рисунок 19б). Мы теперь видим, что путь от одного отверстия до другого во внешнем пространстве может быть большим, а сквозь «тоннель» — совсем коротким. Но это еще не все. Если потянуть за верхний край листа, оставляя на месте нижний край и оба отверстия, то верхняя часть листа будет скользить относительно отверстия В на рис. 19 в. Так как движение относительно, то можно считать, что это верхнее отверстие перемещается среди звезд. Таким образом, расстояние между отверстиями во внешнем пространстве может меняться — увеличиваться и уменьшаться, — а длина «тоннеля» меняться не будет.

Все сказанное об отверстиях и «тоннелях» на нашей двумерной поверхности модели справедливо и в случае отверстий и «тоннелей» в трехмерном пространстве. Только представить себе такую ситуацию с искривленным трехмерным пространством гораздо сложнее. Отверстия А и В снаружи очень похожи на черные дыры. Отличие только в том, что в отверстия можно входить и выходить. Внутри же они соединены коридором и резко отличаются от черных дыр. Здесь можно двигаться и от отверстия А к В и наоборот. Можно так подобрать параметры отверстий и «тоннеля», что гравитационное воздействие на живые существа будет не слишком сильным во время их движения по коридору и вполне ими переносимо.

Теперь ясно, как люди будущего, построившие статический коридор, соединяющий два отверстия А и В, могли бы использовать эту конструкцию. Сначала надо отбуксировать одно из отверстий к далеким звездам, не меняя длины коридора, который может быть пренебрежимо коротким по сравнению с удаленностью отверстий друг от друга во внешнем пространстве (рисунок 19б). Как перемещать в пространстве черные дыры, мы уже разбирали в разделе «Энергия из черных дыр».

А так как наши отверстия снаружи практически не отличаются от черных дыр, то и с ними можно поступать так же.

Наша конструкция теперь может служить Машиной Пространства (пока еще не Машиной Времени). Действительно, путешественник, войдя в отверстие А на рисунке 19б и пройдя короткий тоннель, выйдет из В у далеких звезд. Он потратит на это путешествие совсем немного времени. Для того чтобы попасть к звездам, ему незачем совершать длинный и утомительный межзвездный перелет во внешнем пространстве.

Уже эта Машина Пространства выглядит необычайно интересно. Читатель, надеюсь, простит меня за то, что я описывал некоторые тонкости ее устройства, и в этих местах при чтении требовалась известная внимательность. Результат окупает потраченные усилия.

Теперь мы переходим к наиболее интригующей части. Посмотрим, как отверстия с «тоннелем» переделать в Машину Времени.

Из рассуждений в начале этой главы нам, надеюсь, стало ясно, что для путешествия в прошлое необходимо создать «петли времени». В математических моделях, о которых мы говорили выше, «петли времени» существовали повсюду, но сама модель не имела прямого отношения к действительности.

Сейчас мы увидим, как конструкция со стабильным «тоннелем» может привести согласно расчетам к возникновению «петель времени» в реальной Вселенной. В принципе это возможно сделать даже в окрестности нашей планеты.

Первые наметки такого проекта содержались еще в работе К. Торна и М. Морриса 1987 года. Они затем значительно детализировали и усовершенствовали этот проект в работе с Юртсевером в 1988 году. Когда я прочел эту работу, то предложил свой вариант Машины Времени, опубликованный также осенью 1988 года. Расскажу об этом варианте. Делаю это не только потому, что мне принадлежит авторство, хотя, конечно, каждому легче рассказать о предложенном им самим решении, но главным образом из-за того, что объяснить работу этой версии Машины Времени легче, чем предложенной американскими физиками.

Чтобы проследить за работой Машины Времени, от читателя опять потребуется определенная внимательность. Ничего не поделаешь — это все же Машина Времени. «Все следует сделать простым, насколько это возможно, но не проще», — говорил Эйнштейн. Те из читателей, кто не склонен вникать в тонкости, пусть пропустят следующие пару страниц и обратятся сразу к результату.

Итак, представим себе два отверстия А и В, расположенных на значительном расстоянии друг от друга, но соединенных коротким тоннелем. Поместим у отверстий А и В одинаковые часы. Пусть они находятся все же на достаточном расстоянии от отверстий, чтобы на их ход практически не влияло сильное гравитационное поле отверстий. Однако расстояние должно быть все же мало по сравнению с расстоянием между А и В во внешнем пространстве.

Представим далее путешественника, который отправился от отверстия А и движется к В во внешнем пространстве. Пусть он перемещается не слишком быстро, чтобы время у него текло практически так же, как у А. В момент начала его путешествия одновременно запускают часы А и В. Пусть он затратил на это путешествие 10 лет, что и фиксируется по часам у отверстия В, а затем входит в отверстие В и возвращается через тоннель к А. Так как тоннель очень короткий, то на его преодоление практически совсем не затрачивается времени, то есть путешественник возвращается к А почти в тот же момент, что вошел в В. Пока ничего необычного не произошло — наш герой вернулся к А через 10 лет после отправления.

Изменим теперь ситуацию. Пусть отверстие А все время неподвижно, а отверстие В с большой скоростью обращается вокруг отверстия А. Включим часы А и В одновременно в момент начала кружения В. Часы В, участвуя в стремительном движении вокруг А, согласно выводам специальной теории относительности будут идти медленнее, чем часы А, и будут все больше и больше отставать от А. Пусть скорость их вращения такова, что они идут вдвое медленнее, чем часы А. Значит, когда по часам А пройдет 10 лет, по часам В только 5, если по А пройдет 30 лет, по часам В 15 лет и т. д.

Все это справедливо, если часы А и В сверяются во внешнем пространстве. Наблюдатель у часов А будет реально видеть, что часы В замедлили свой бег и отстали от А. При наблюдениях в телескоп он прямо видит, что секундная стрелка часов В движется вдвое медленнее, чем стрелка его часов. Наблюдатель, находящийся все время у отверстия В (и движущийся с ним), также увидит, что его часы отстают от часов А.

Но совсем иная картина представится наблюдателям, если они будут смотреть друг на друга через «тоннель». Поскольку он очень короткий, то каждый наблюдатель видит, что и часы А, и часы В практически находятся рядом. И хотя силы тяготения и инерции в тоннеле заметны, они из-за его короткости не создают больших перепадов физических условий для часов, и они наблюдателям через тоннель кажутся идущими практически одинаково, показывают одинаковое время.

Итак, в зависимости от способа наблюдения (а лучше сказать — от способа синхронизации часов) результат получается разный! И дело здесь не в каких-то недостатках одного из методов синхронизации — просто свойства потока времени во внешнем пространстве и в «тоннеле» теперь разные!

Посмотрим, к чему это приведет. Пусть опять путешественник отправляется от А к орбите кружения отверстия В и выбирает направление своего прямолинейного движения во внешнем пространстве так, чтобы подойти к орбите В в тот момент, когда в этой же точке окажется стремительно движущееся отверстие В. Видя подлетающее отверстие, путешественник набирает скорость, равную скорости отверстия В, ныряет в него и через «тоннель» возвращается к отверстию А. Все это нетрудно представить.

Мы пока не заботимся о перегрузках, действующих на путешественника. В принципе всегда можно подобрать параметры движений так, чтобы перегрузки были приемлемыми. Все наше внимание сосредоточено сейчас на ходе течения времени, на его темпе.

Проследим внимательно за движением путешественника. Допустим, он отправляется в полет по внешнему пространству, когда отверстие В уже долго кружило вокруг А и часы у В заметно отстали от часов А, скажем, путешественник стартует, когда часы А показывали 20 лет (после начала кружения В), а часы В, шедшие вдвое медленнее, показывали только 10 лет. Все это, разумеется, с точки зрения наблюдателей из внешнего пространства.

Пусть путешественник затратил на полет к В по-прежнему 10 лет по часам А; следовательно, по часам В проходит вдвое меньше времени, то есть всего 5 лет. Так как старт произошел по часам В в 10 лет, то в момент прибытия его к В они показывают 15 лет с начала их кружения. К этому моменту часы А «натикали» уже 30 лет.

Теперь путешественник ныряет в отверстие В. В этот момент он, как и любой наблюдатель у В, может взглянуть сквозь «тоннель» на часы А и увидит, как мы уже установили, что часы А показывают то же время, что и В, то есть 15 лет после начала кружения! Видя перед собой эти часы, он быстро проходит сквозь короткий «тоннель» и практически в тот же момент появляется из отверстия А, откуда он и начинал свое путешествие.

Но он ведь начинал свое путешествие, когда часы А показывали 20 лет! А вернулся, когда на них — 15 лет! То есть он вернулся раньше старта! Свершилось то, что казалось невозможным — путешественник попал в прошлое! Говоря словами Гамлета, «раньше это считалось парадоксом, а теперь доказано».

Если у кого-то из читателей осталось беспокойство за путешественника, ныряющего в стремительно мчащееся отверстие В и испытывающего после этого еще и центробежные ускорения, то пусть он не волнуется. После достаточно продолжительного кружения, когда часы В значительно отстали от часов А, отверстие В можно остановить. Накопленного отставания часов В достаточно. Конструкция уже превратилась в Машину Времени.

Такое же путешествие от А к В во внешнем пространстве, и затем к А сквозь «тоннель», будет возвращать космонавта в его прошлое.

Эта же Машина Времени может служить и для «полета» в будущее. Для этого надо проходить «тоннель» в обратном направлении. Надо, отправляясь от А, сначала пройти по «тоннелю» к отверстию В, выйти из него, а затем по внешнему пространству совершить перелет к А. Вернувшись, вы попадете в достаточно далекое будущее. Заметьте, что вы двигались с умеренной скоростью и замедления времени, предсказываемого специальной теорией относительности, для вашего полета практически не существовало. Здесь вас переносит в будущее именно Машина Времени.

Наконец, подчеркнем еще следующее. Для того, чтобы переноситься в прошлое или будущее с помощью Машины Времени, обязательно надо двигаться! Нельзя, подобно герою повести Г. Уэллса, неподвижно сидеть в кресле «машины», оставаясь все время на одном месте, и ощущать лишь ее тряску. В нашем случае надо перемещаться во внешнем пространстве и по «тоннелю». При этом, чтобы попасть, например, в прошлое, скорость движения должна быть все же не очень малой. Иначе долгие годы путешествия скрадут тот промежуток времени перемещения в прошлое, которое дает Машина Времени.