Глава 11 ВНУТРЕННЕЕ УСТРОЙСТВО ДИЭЛЕКТРИКОВ

We use cookies. Read the Privacy and Cookie Policy

Глава 11

ВНУТРЕННЕЕ УСТРОЙСТВО ДИЭЛЕКТРИКОВ

§1. Молекулярные диполи

§2. Электронная поляризация

§3. Полярные молекулы; ориентационная поляризация

§4. Электрические поля в пустотах диэлектрика

§5. Диэлектрическая проницаемость жидкостей; формула Клаузиуса — Моссотти

§6. Твердые диэлектрики

§7. Сегнетоэлектричество; титанат бария

Повторить: гл. 3 (вып. 3) «Как возникает показатель преломления», гл. 40 (вып. 4) «Принципы статистической механики »

§ 1. Молекулярные диполи

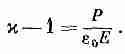
В этой главе мы поговорим о том, почему вещество бывает диэлектриком. В предыдущей главе мы указывали, что свойства электри­ческих систем с диэлектриками можно было бы понять, предположив, что электрическое поле, действуя на диэлектрик, индуцирует в атомах дипольный момент. Именно, если элект­рическое поле Е индуцирует средний диполь­ный момент в единице объема Р, то диэлектри­ческая проницаемость х дается выражением

(11.1)

О применениях этого выражения мы уже говорили; сейчас же нам нужно обсудить меха­низм возникновения поляризации внутри ма­териала под действием электрического поля. Начнем с самого простого примера — поляри­зации газов. Но даже в газах возникают слож­ности: существуют два типа газов. Молекулы некоторых газов, например кислорода, в каж­дой молекуле которого имеются два симметрич­ных атома, лишены собственного дипольного момента. Зато молекулы других газов, вроде водяного пара (у которого атомы водорода и кислорода образуют несимметричную молекулу), обладают постоянным электрическим дипольным моментом. Как мы отмечали в гл. 6 и 7, в молекуле водяного пара атомы водорода в среднем имеют положительный заряд, а атом кислорода — отрицательный. Поскольку цент­ры тяжести положительного и отрицательного зарядов не совпадают, то распределение всего заряда в молекуле обладает дипольным моментом.

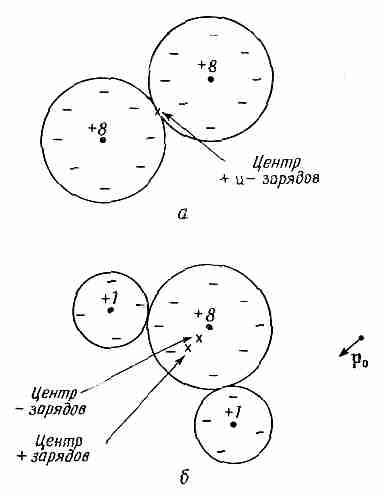
Фиг. 11.1. Молекула кислорода с нулевым дипольным моментом (а) и моле­кула воды с постоянным дипольным моментом р0 (б).

Такая молекула называется полярной молекулой. А у кисло­рода вследствие симмет­рии молекулы центр тяжести и положитель­ных, и отрицательных зарядов один и тот же, так что это неполярная молекула. Она, правда,

может стать диполем, если ее поместить в электрическое поле. Формы этих двух типов молекул нарисованы на фиг. 11.1.

§ 2. Электронная поляризация

Займемся сначала поляризацией неполярных молекул. Начнем с простейшего случая одноатомного газа (например, гелия). Когда атом такого газа находится в электрическом поле, электроны его тянутся в одну сторону, а ядро — в другую, как показано на рис. 10.4 (стр. 200). Хотя атомы имеют очень боль­шую жесткость по отношению к электрическим силам, которые мы можем приложить к ним на опыте, центры зарядов чуть-чуть смещаются относительно друг друга и индуцируется дипольный момент. В слабых полях величина смещения, а следовательно, и дипольного момента пропорциональна напряженности элект­рического поля. Смещение электронного распределения, ко­торое приводит к этому типу индуцированного дипольного момента, называется электронной поляризацией.

Мы уже обсуждали воздействие электрического поля на атом в гл. 31 (вып. 3), когда занимались теорией показателя преломления. Подумав немного, вы сообразите, что теперь нужно сделать то же, что и тогда. Только теперь нас заботят поля, не меняющиеся со временем, тогда как показатель пре­ломления был связан с полями, зависящими от времени.

В гл. 31 (вып. 3) мы предполагали, что центр электронного заряда атома, помещенного в осциллирующее электрическое поле, подчиняется уравнению

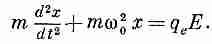
(11.2)

Первый член — это произведение массы электрона на его ускорение, а второй — возвращающая сила; справа стоит сила, действующая со стороны внешнего электрического поля. Если электрическое поле меняется с частотой w, то уравнение (11.2)

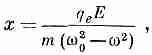
допускает решение

(11.3)

имеющее резонанс при w=w0. Когда раньше мы нашли это решение, то интерпретировали w0 как частоту, при которой атом поглощает свет (она лежит либо в оптической, либо в ультрафиолетовой области, в зависимости от атома). Для нашей цели, однако, достаточно случая постоянных полей, т.е. w=0; поэтому мы можем пренебречь членом с ускорением в (11.2) и получаем смещение

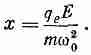
(11.4)

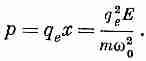
Отсюда находим дипольный момент р одного атома

(11.5)

В таком подходе дипольный момент р действительно пропор­ционален электрическому полю. Обычно пишут

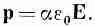
(11.6)

(Снова e0 вошло по историческим причинам.) Постоянная a называется поляризуемостью атома и имеет размерность L3. Это мера того, насколько легко индуцировать электрическим полем дипольный момент у атома. Сравнивая

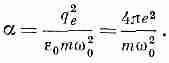
(11.5) и (11.6), получаем, что в нашей простой теории

(11.7)

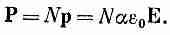
Если в единице объема содержится N атомов, то поляри­зация (дипольный момент единицы объема) дается формулой

(11.8)

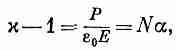
Объединяя (11.1) и (11.8), получаем

(11.9)

или в силу (11.7)

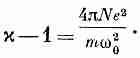
(11.10)

С помощью уравнения (11.9) можно предсказать, что ди­электрическая проницаемость х различных газов должна зависеть от плотности газа и от резонансной частоты w0.

Наша формула, конечно, лишь очень грубое приближение, потому что в уравнении (11.2) мы воспользовались моделью, игнорирующей тонкости квантовой механики. Например, мы считали, что атом имеет только одну резонансную частоту, тогда как на самом деле их много. Чтобы по-настоящему вычислить поляризуемость атомов, нужно воспользоваться последовательной квантовомеханической теорией, однако и классический подход, изложенный выше, дает вполне разумную оценку.

Посмотрим, сможем ли мы получить правильный порядок величины диэлектрической проницаемости какого-нибудь ве­щества. Возьмем, к примеру, водород. Мы уже оценивали (вып. 4, гл. 38) энергию, необходимую для ионизации атома водорода, и получили приближенно

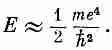
(11.11)

Для оценки собственной частоты w0 можно положить эту энер­гию равной ћw0— энергии атомного осциллятора с собственной частотой w0. Получаем

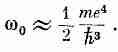
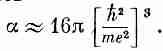
Пользуясь этой величиной в уравнении (11.7), находим элек­тронную поляризуемость

(11.12)

Величина (h2/mez) есть радиус основной орбиты атома Бора (см. вып. 4, гл. 38), равный 0,528 А. При нормальном давлении и температуре (1 атм, 0°С) в газе на 1 см3приходится 2,69·1019 атомов, и уравнение (11.9) дает

c= 1+ (2,69·1019) 16p (0,528·10-8)3 = 1,00020. (11.13) Измеренная на опыте диэлектрическая проницаемость равна

cэксп = 1,00026.

Видите, наша теория почти правильна. Лучшего нельзя было и ожидать, потому что измерения проводились, конечно, с обычным водородом, обладающим двухатомными молекулами, а не одиночными атомами. Не следует удивляться тому, что поляризация атомов в молекуле не совсем такая, как поляри­зация отдельных атомов. На самом деле молекулярный эффект не столь велик. Точное квантовомеханическое вычисление вели­чины a для атомов водорода дает результат, превышающий (11.12) примерно на 12% (вместо 16pполучается 18p), поэтому он предсказывает для диэлектрической проницаемости значе­ние, более близкое к наблюденному. Во всяком случае, со­вершенно очевидно, что наша модель диэлектрика вполне хороша.

Еще одна проверка нашей теории. Попробуем применить уравнение (11.12) к атомам с большей частотой возбуждения. Например, чтобы отобрать электрон у гелия, требуется 24,5 в, тогда как для ионизации водорода необходимы 13,5 в. Поэтому мы предположим, что частота поглощения w0 для гелия должна быть примерно в два раза больше, чем для водорода, а a должна быть меньше в четыре раза. Мы ожидаем, что

хгелнй»1,000050, а экспериментально получено

xгелий=1,000068,

так что наши грубые оценки показывают, что мы на верном пути. Итак, мы поняли диэлектрическую проницаемость не­полярного газа, но только качественно, потому что пока мы еще не использовали правильную атомную теорию движения атомных электронов.

§ 3. Полярные молекулы; ориентационная поляризация

Теперь рассмотрим молекулу, обладающую постоянным дипольным моментом р0 , например молекулу воды. В отсутст­вие электрического поля отдельные диполи смотрят в разных направлениях, так что суммарный момент в единице объема равен нулю. Но если приложить электрическое поле, то сразу же происходят две вещи: во-первых, индуцируется добавочный дипольный момент из-за сил, действующих на электроны; эта часть приводит к той же самой электронной поляризуемости, которую мы нашли для неполярной молекулы. При очень точ­ном исследовании этот эффект, конечно, нужно учитывать, но мы пока пренебрежем им. (Его всегда можно добавить в конце.) Во-вторых, электрическое поле стремится выстроить отдельные диполи, создавая результирующий момент в единице объема.

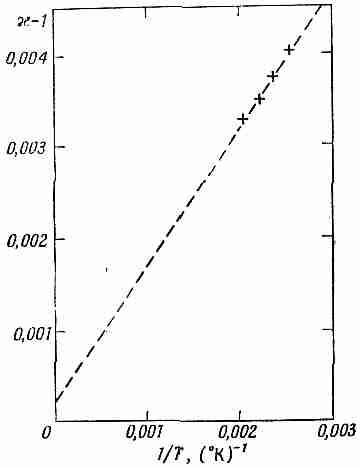
Фиг. 11.2. В газе полярных молекул отдельные моменты ориен­тированы случайным образом, средний момент в небольшом объеме равен нулю (а); под действием электрического поля в среднем возникает некоторое выстраивание молекул (б).

Если бы в газе выстроились все диполи, поляризация была бы очень большой, но этого не происходит. При обычных темпе­ратурах и напряженностях поля столкновения молекул при их тепловом движении не позволяют им как следует выстроить­ся. Но некоторое выстраивание все же происходит, а отсюда и небольшая поляризация (фиг. 11.2). Возникающая поляри­зация может быть подсчитана методами статистической меха­ники, описанными в гл. 40 (вып. 4).

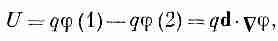
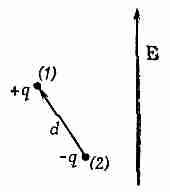
Чтобы использовать этот метод, нужно знать энергию диполя в электрическом поле. Рассмотрим диполь с моментом р0 в электрическом поле (фиг. 11.3). Энергия положительного за­ряда равна qj (1), а энергия отрицательного есть —qj(2). Отсюда получаем энергию диполя

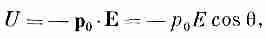
или

(11.14)

где q — угол между р0 и Е. Как и следовало ожидать, энергия становится меньше, когда диполи выстраиваются вдоль поля. Теперь с помощью методов статистической механики мы выясним, насколько сильно диполи выстраиваются. В гл. 40 (вып. 4) мы нашли, что в состоянии теплового равновесия относительное число молекул с потенциальной энергией U пропорционально

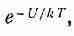
(11.15)

Фие. 11.3. Энергия диполя р0 в поле Е равна —р0·Е.

где U (х, у, z) — потенциальная энергия как функция поло­жения. Оперируя теми же аргументами, можно сказать, что если потенциальная энергия как функция угла имеет вид (11.14), то число молекул под углом 0, приходящееся на единичный телесный угол, пропорционально ехр (— U/kT).

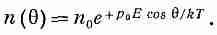
Полагая число молекул на единичный телесный угол, на­правленных под углом q, равным n(q), имеем

(11.16)

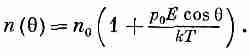
Для обычных температур и полей показатель экспоненты мал, и, разлагая экспоненту, можно воспользоваться прибли­женным выражением

(11.17)

Найдем n , проинтегрировав (11.17) по всем углам; результат должен быть равен N, т.е. числу молекул в единице объема. Среднее значение cos q при интегрировании по всем углам есть нуль, так что интеграл равен просто n0 , умноженному на полный телесный угол 4p. Получаем

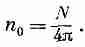
(11.18)

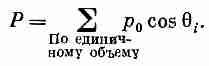
Из (11.17) видно, что вдоль поля (cosq=1) будет ориен­тировано больше молекул, чем против поля (cosq = -1). Поэтому в любом малом объеме, содержащем много молекул, возникнет суммарный дипольный момент на единицу объема, т.е. поляризация Р. Чтобы вычислить Р, нужно знать векторную сумму всех молекулярных моментов в единице объема. Мы зна­ем, что результат будет направлен вдоль Е, поэтому нужно только просуммировать компоненты в этом направлении (ком­поненты, перпендикулярные Е, при суммировании дадут нуль):

Мы можем оценить сумму, проинтегрировав по угловому распределению. Телесный угол, отвечающий q, есть 2psin qdq; отсюда

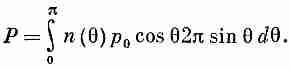
(11.19)

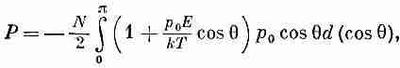
Подставляя вместо n(q) его выражение из (11.17), имеем

что легко интегрируется и приводит к следующему результату:

(11.20)

Поляризация пропорциональна полю Е, поэтому диэлектри­ческие свойства будут обычные. Кроме того, как мы и ожидаем, поляризация обратно пропорциональна температуре, потому что при более высоких температурах столкновения больше разрушают выстроенность. Эта зависимость вида 1/T называется законом Кюри. Квадрат постоянного момента р0появляется по следующей причине: в данном электрическом поле выстраиваю­щая сила зависит от р0, а средний момент, возникающий при выстраивании, снова пропорционален р0. Средний индуцируе­мый момент пропорционален р02

Теперь посмотрим, насколько хорошо уравнение (11.20) согласуется с экспериментом. Возьмем водяной пар. Поскольку мы не знаем, чему равно р0, то не можем прямо вычислить и Р, но уравнение (11.20) предсказывает, что x-1 должна ме­няться обратно пропорционально температуре, и это нам сле­дует проверить.

Из (11.20) получаем

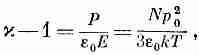
(11.21)

так что x-1 должна меняться прямо пропорционально плот­ности N и обратно пропорционально абсолютной температуре. Диэлектрическая проницаемость была измерена при несколь­ких значениях давления и температуры, выбранных таким об­разом, чтобы число молекул в единице объема оставалось постоянным. (Заметим, что, если бы все измерения выполнялись при постоянном давлении, число молекул в единице объема уменьшалось бы линейно с повышением температуры, а х-1 изменялась бы как T-2, а не как T-1.)

Фиг. 11.4. Измеренные значе­ния диэлектрической проницае­мости водяного пара при не­скольких температурах.

На фиг. 11.4 мы отложили измеренные значения к — 1 как функ­цию 1/T. Зависимость, предсказываемая форму­лой (11.21), выполняется хорошо.

Есть еще одна особен­ность диэлектрической проницаемости полярных молекул — ее изменение в зависимости от частоты внешнего поля. Благодаря тому что молекулы имеют момент инерции, тяжелым молекулам тре­буется определенное время, чтобы повернуться в направлении поля. Поэтому, если использовать частоты из верхней микро­волновой зоны или из еще более высокой, полярный вклад в диэлектрическую проницаемость начинает спадать, так как молекулы не успевают следовать за полем. В противополож­ность этому электронная поляризуемость все еще остается неизменной вплоть до оптических частот, поскольку инерция

электронов меньше.

§ 4. Электрические поля в пустотах диэлектрика

Теперь мы переходим к интересному, но сложному вопросу о диэлектрической проницаемости плотных веществ. Возьмем, например, жидкий гелий, или жидкий аргон, или еще какое-нибудь неполярное вещество. Мы по-прежнему ожидаем, что у них есть электронная поляризуемость. Но в плотных средах значение Р может быть велико, поэтому в поле, действующее на отдельный атом, вклад будет давать поляризация атомов, находящихся по соседству. Возникает вопрос, чему равно электрическое поле, действующее на отдельный атом?

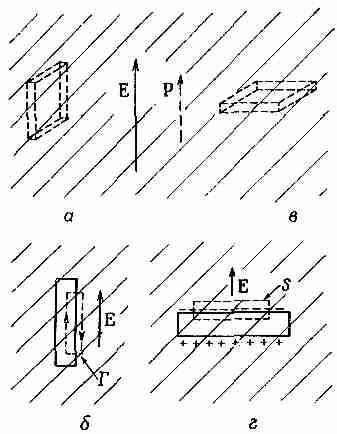
Фиг. 11.5. Поле внутри щели, вырезанной в диэлектрике, за­висит от ее формы, и ориента­ции.

Вообразите, что между пластинами конденсатора находится жидкость. Если пластины заряжены, они создадут в жидкости элек­трическое поле. Но каждый атом имеет заряды, и пол­ное поле Е есть сумма обоих этих вкладов. Это истинное электрическое поле в жидкости меняется очень-очень быстро от точки к точке. Оно чрезвычайно велико внутри атомов, особенно вблизи ядра, и сравнительно мало между атомами. Разность потенциалов между пластинами есть интеграл от этого полного поля. Если мы пренебрежем всеми быстрыми изменениями, то можем представить себе некое среднее электрическое поле Е, равное как раз V/d. (Именно это поле мы исполь­зовали в предыдущей главе.) Это поле мы должны себе пред­ставлять как среднее по пространству, содержащему много атомов.

Вы можете подумать, что «средний» атом в «среднем» поло­жении почувствует именно это среднее поле. Но все не так просто, и в этом можно убедиться, представив, что в диэлект­рике имеются отверстия разной формы. Предположим, что мы вырезали в поляризованном диэлектрике щель, ориентирован­ную параллельно полю (фиг. 11.5, а). Поскольку мы знаем, что СXE = 0, то линейный интеграл от Е вдоль кривой Г, на­правленной так, как показано на фиг. 11.5, б, должен быть равен нулю. Поле внутри щели должно давать такой вклад, который в точности погасит вклад от поля вне щели. Поэтому поле E0 в центре длинной тонкой щели равно Е, т.е. среднему электрическому полю, найденному в диэлектрике.

Рассмотрим теперь другую щель, повернутую своей ши­рокой стороной перпендикулярно Е (фиг. 11.5, в). В этом случае поле e0 в щели не совпадает с Е, потому что на стенках щели возникают поляризационные заряды. Применив закон Гаусса к поверхности S, изображенной на фиг. 11.5, г, мы находим, что поле Ей внутри щели дается выражением

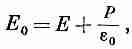
(11.22)

где Е, как и раньше,— электрическое поле в диэлектрике. (Гауссова поверхность охватывает поверхностный поляриза­ционный заряд sпол = Р.) Мы отмечали в гл. 10, что e0Е + Р часто обозначают через D, поэтому e0Е0 = D0равно величине D в диэлектрике.

В ранний период истории физики, когда считалось очень важным определять каждую величину прямым экспериментом, физики были очень довольны, обнаружив, что они могут опре­делить то, что понимают под Е и D в диэлектрике, не ползая в промежутках между атомами. Среднее поле Е численно равно полю Е0, измеренному в щели, параллельной полю. А поле D могло быть измерено с помощью Е0, найденной в щели, перпен­дикулярной полю. Но никто эти поля никогда не измерял (таким способом, во всяком случае), так что это одна из многих бесплодных проблем.

В большинстве жидкостей, не слишком сложных по своему строению, каждый атом в среднем так окружен другими ато­мами, что можно с хорошей точностью считать его находящимся в сферической полости. И тогда мы спросим: «Чему равно поле в сферической полости?» Мы замечаем, что вырезание сфери­ческой дырки в однородном поляризованном диэлектрике равно­сильно отбрасыванию шарика из поляризованного материала, так что мы можем ответить на этот вопрос. (Мы должны пред­ставить себе, что поляризация была «заморожена» до того, как мы вырезали дырку.) Однако в силу принципа суперпозиции поле внутри диэлектрика, до того как оттуда был вынут шарик, есть сумма полей от всех зарядов вне объема шарика плюс полей от зарядов внутри поляризованного шарика.

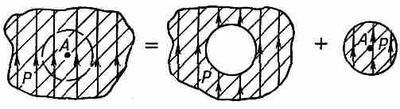
Фиг. 11.6. Поле в любой точке А диэлектрика можно представить в виде суммы поля сферической дырки и поля сферического вкладыша.

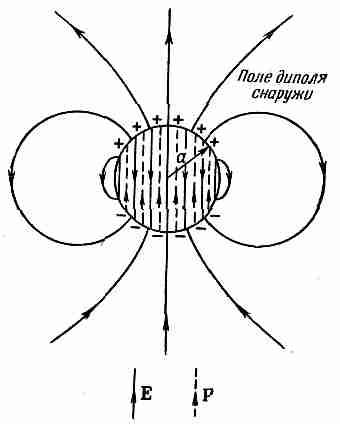
Фиг. 11.7. Электрическое поле однородно поляризо­ванного шарика.

Следова­тельно, если поле внутри однородного диэлектрика мы назовем Е, то можно записать

E=Eдырка+Eшарнк,

(11.23)

где Eдырка — поле в дырке, а Eшарик — по­ле в однородно поля­ризованном шарике (фиг. 11.6). Поле одно­родно поляризованного шарика показано на фиг. 11.7. Электрическое поле внутри шарика однородно и равно

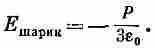
(11.24)

С помощью (11.23) получаем

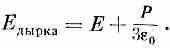
(11.25)

Поле в сферической полости больше среднего поляна величину Р/Зe0. (Сферическая дырка дает поле, находящееся на 1/3 пути от поля параллельной щели к полю перпендикулярной щели.)

§ 5. Диэлектрическая проницаемость жидкостей; формула Клаузиуса — Моссотти

В жидкости мы ожидаем, что поле, поляризующее отдель­ный атом, скорее похоже на Едырка, чем просто на Е. Если взять Eдырка из (11.25) в качестве поляризующего поля, вхо­дящего в (11.6), то уравнение (11.8) приобретет вид

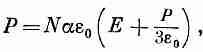
(11.26)

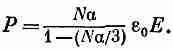
или

(11.27)

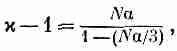
Вспоминая, что х-1 как раз равна Р/e0Е, получаем

(11.28)

что определяет диэлектрическую проницаемость жидкости и через атомную поляризуемость a. Это формула Клаузиуса — Моссотти.

Если Naочень мало, как, например, для газа (потому что там мала плотность N), то членом Na/3 можно пренебречь по сравнению с 1, и мы получаем наш старый результат — уравне­ние (11.9), т.е.

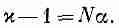
(11.29)

Давайте сравним уравнение (11.28) с некоторыми экспери­ментальными данными. Сначала стоит обратиться к газам, для которых из измерений x можно с помощью уравнения (11.29) найти значение а. Так, для дисульфида углерода при нулевой температуре по Цельсию диэлектрическая проницаемость равна 1,0029, так что Na= 0,0029. Плотность газа легко вычислить, а плотность жидкостей можно найти в справочниках. При 20°C плотность жидкого CS2 в 381 раз выше плотности газа при 0°С, Это значит, что N в 381 раз больше в жидкости, чем в газе, а отсюда (если сделать допущение, что исходная атомная поля­ризуемость дисульфида углерода не меняется при его конден­сации в жидкое состояние) Naв жидкости в 381 раз больше 0,0029, или равно 1,11. Заметьте, что Na/З составляет почти 0,4. С помощью этих чисел мы предсказываем, что величина диэлектрической проницаемости равна 2,76, что достаточно хорошо согласуется с наблюденным значением 2,64.

В табл. 11.1 мы приводим ряд экспериментальных данных по разным веществам, а также значения диэлектрической проницаемости, вычисленной, как только что было описано, no формуле (11.28).

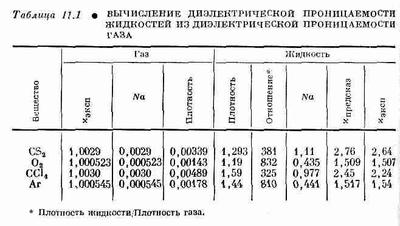
Согласие между опытом и теорией для аргона и кислорода даже лучше, чем для CS2, и не столь хорошее для четыреххлористого углерода. В целом результаты показывают, что уравнение (11.28) работает с хорошей точностью.

Наш вывод уравнения (11.28) справедлив только для элек­тронной поляризации в жидкостях. Для полярных молекул вроде Н2O он неверен. Если провести такие же вычисления для воды, то для Na. получим значение 13,2, что означает, что диэлектрическая проницаемость этой жидкости отрицательна, тогда как опытное значение x равно 80. Дело здесь связано с неправильной трактовкой постоянных диполей, и Онзагер указал правильный способ решения. Мы не можем сейчас останавливаться на этом вопросе, но если он вас интересует, то подробно это обсуждается в книге Киттеля «Введение в фи­зику твердого тела».

§ 6. Твердые диэлектрики

Обратимся теперь к твердым телам. Первый интересный факт относительно твердых тел заключается в том, что у них бывает постоянная поляризация, которая существует даже и без приложения внешнего электрического поля. Примеры можно найти у веществ типа воска, который содержит длинные молекулы с постоянным дипольным моментом. Если растопить немного воску и, пока он еще не затвердел, наложить на него сильное электрическое поле, чтобы дипольные моменты частично выстроились, то они останутся в таком положении и после того, как воск затвердеет. Твердое вещество будет обладать постоянной поляризацией, которая остается и в отсутствие поля. Такое вещество называется электретом.

На поверхности электрета расположены постоянные поляри­зационные заряды. Электрет представляет собой электрический аналог магнита, однако пользы от него гораздо меньше, потому что свободные заряды воздуха притягиваются к его поверхности и в конце концов нейтрализуют поляризационные заряды. Электрет «разряжается» и заметного внешнего поля не со­здает.

Постоянная внутренняя поляризация Р встречается и у не­которых кристаллических веществ. В таких кристаллах каждая элементарная ячейка решетки обладает одним и тем же постоян­ным дипольным моментом (фиг. 11.8). Все диполи направлены в одну сторону даже в отсутствие электрического поля. Многие сложные кристаллы обладают такой поляризацией; обычно мы этого не замечаем, потому что создаваемое ими внешнее поле, как и у электретов, разряжается.

Если, однако, внутренние диполъные моменты кристалла меняются, то внешнее поле становится заметным, потому что блуждающие заряды не успевают собраться и нейтрализовать поляризационные заряды. Если диэлектрик находится в кон­денсаторе, свободные заряды индуцируются на электродах. Моменты могут, например, измениться вследствие теплового расширения, если нагреть диэлектрик. Такой эффект называется пироэлектричеством. Аналогично, если менять напряжения в кристалле, скажем, сгибая его, то момент может снова немного измениться, и тогда обнаружится слабый электрический эффект, называемый пьезоэлектричеством.

Для кристаллов, не обладающих постоянным моментом, можно развить теорию диэлектрической проницаемости, куда включается электронная поляризуемость атомов. Делается это почти так же, как для жидкостей. Некоторые кристаллы имеют внутренние моменты, и вращение их также вносит вклад в x. В ионных кристаллах, таких, как NaCl, возникает также ионная поляризуемость. Кристалл состоит из положительных и отрицательных ионов, расположенных в шахматном порядке, и в электрическом поле положительные ионы тянутся в одну сторону, а отрицательные — в другую; возникает результи­рующее смещение положительных и отрицательных зарядов, а следовательно, и объемная поляризация. Мы могли бы оце­нить величину ионной поляризуемости, зная жесткость кри­сталлов соли, но мы не будем сейчас останавливаться на этом вопросе.

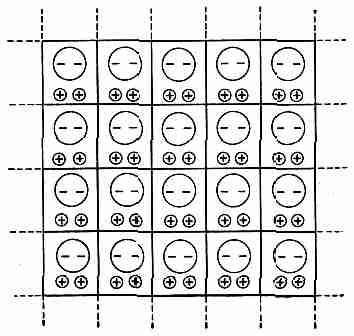
Фиг. 11.8. Сложная кристаллическая решетка может иметь постоянную внутреннюю поля­ризацию Р.

§ 7. Сегиетоэлектричество; титанат бария

Мы опишем здесь особый класс кристаллов, которые, можно сказать, почти случайно обладают «встроенным» постоянным электрическим моментом. Ситуация здесь настолько критична, что, если слегка увеличить температуру выше некоторой, кри­сталл этого класса совсем потеряет постоянный момент. С дру­гой стороны, если структура кристалла близка к кубической, так что электрические моменты могут располагаться в разных направлениях, можно обнаружить большие изменения полного момента при изменении приложенного электрического поля. Все моменты перевертываются в направлении поля, и мы полу­чаем большой эффект. Вещества, обладающие такого рода постоянным моментом, называются сегнетоэлектриками. Мы хотели бы объяснить механизм сегнетоэлектричества на частном примере какого-нибудь сегнетоэлектрического ма­териала. Сегнетоэлектрические свойства могут возникать нес­колькими путями; однако мы разберем только один из них на примере таинственного титаната бария (BaТiO3). Это вещество обладает кристаллической решеткой, основная ячейка кото­рого изображена на фиг. 11.9. Оказывается, что выше некоторой температуры (а именно 118°С) титанат бария — обычный ди­электрик с огромной диэлектрической проницаемостью, а ниже этой температуры он неожиданно приобретает постоянный момент.

При вычислении поляризации твердых тел мы должны сна­чала найти локальные поля в каждой элементарной ячейке. Причем для этого нужно ввести поля самой поляризации, как это делалось в случае жидкости. Но кристалл — не однородная жидкость, так что мы не можем взять в качестве локального поля то, что мы нашли в сферической дыре. Если мы сделаем это для кристалла, то окажется, что множитель 1/3 в уравнении (11.24) слегка изменится, но ненамного. (Для простого куби­ческого кристалла он равен в точности 1/3.) Поэтому предпо­ложим в нашем предварительном обсуждении, что этот множитель для BaTi03 действительно равен 1/3.

Далее, когда мы писали уравнение (11.28), вам, наверное, было интересно знать, что случится, если Naстанет больше 3. На первый взгляд величина x должна бы стать отрицательной. Но такого наверняка не может быть. Посмотрим, что произойдет, если в каком-нибудь определенном кристалле постепенно увеличивать значение a.

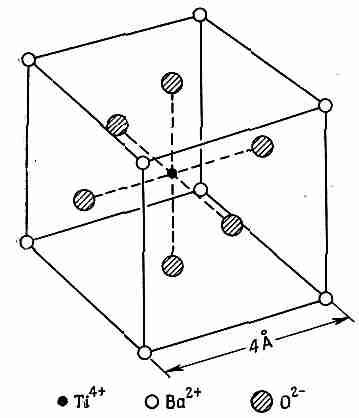
Фиг. 11.9. Элементарная ячей­ка ВаТiO3.

Атомы в действительности запол­няют большую часть пространства; показаны только положения их центров.

По мере роста a растет и поляризация, создавая большее локаль­ное поле. Но увеличившее­ся локальное поле заполяризует атом еще больше, дополнительно усиливая само локальное поле. Если атомы достаточно «податливы», про­цесс продолжается; возникает своего рода обратная связь, приводящая к безудержному росту поляризации (если пред­положить, что поляризация каждого атома увеличивается пропорционально полю). Условие «разгона» возникает при Na = 3. Поляризация, конечно, не обращается в бесконечность, потому что при сильных полях пропорциональность между индуцированным моментом и электрическим полем нарушается, так что наши формулы становятся неправильными. А полу­чается то, что в решетку, оказывается, «встроена» большая внутренняя самопроизвольная поляризация.

В случае ВаТiO3 вдобавок к электронной поляризации имеется довольно большая ионная поляризация, обусловлен­ная, как предполагают, ионами титана, которые могут слегка сдвигаться внутри кубической решетки. Решетка сопротив­ляется большим смещениям, так что ион титана, переместив­шись на небольшое расстояние, затормаживается и останавли­вается. Но тогда у кристаллической решетки образуется по­стоянный дипольный момент.

У большинства сегнетоэлектрических кристаллов такая ситуация действительно возникает при всех достижимых тем­пературах. Однако титанат бария представляет особый интерес: он так деликатно устроен, что при малейшем уменьшении Na момент «высвобождается». Поскольку N с повышением температуры уменьшается (вследствие теплового расширения), то можно изменять Na, меняя температуру. Ниже критической температуры момент сразу образуется, и тогда, накладывая внешнее поле, поляризацию легко повернуть и закрепить в нужном направлении.

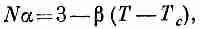
Попробуем разобраться в происходящем более подробно. Назовем критической температуру Тс, при которой Na равно в точности 3. При увеличении температуры значение N немного уменьшается вследствие расширения решетки. Поскольку рас­ширение мало, мы можем сказать, что вблизи критической температуры

(11.30)

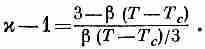
где b — малая константа, того же порядка величины, что и коэф­фициент теплового расширения, т. е. около 10-5—10-6град-1. Подставляя это в выражение (11.28), получаем

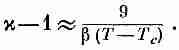
Поскольку мы считаем величину b (Т -Тс) малой по сравне­нию с единицей,можно записать приближенно

(11.31)

Это, конечно, справедливо только для Т>Тс. Мы видим, что если температура чуть выше критической, то величина х огромна. Из-за того, что Na так близко к 3, возникает гро­мадный эффект усиления и диэлектрическая проницаемость легко достигает величины от 50 000 до 100 000. Она тоже весьма чувствительна к температуре. При увеличении температуры диэлектрическая проницаемость уменьшается обратно про­порционально температуре, но в отличие от дипольного газа, где разность x-1 обратно пропорциональна абсолютной температуре, у сегнетоэлектриков она меняется обратно пропор­ционально разности между абсолютной и критической темпе­ратурами (этот закон называется законом Кюри — Вейсса).

Что получается, когда мы понижаем температуру до кри­тического значения? Если кристаллическая решетка состоит из элементарных ячеек вида, изображенного на фиг. 11.9, то, очевидно, можно выбрать цепочки ионов вдоль вертикальных линий. Одна из них состоит попеременно из ионов кислорода и титана. Имеются и другие цепочки, состоящие либо из ионов бария, либо из ионов кислорода, но расстояния между ионами вдоль таких линий оказываются больше. Используем простую модель, вообразив ряд ионных цепочек (фиг. 11.10, а). Вдоль цепочки, которую мы назовем главной, расстояние между ионами равно а, что составляет половину постоянной решетки; поперечное

расстояние между одинако­выми цепочками равно 2а.

Фиг. 11.10. Модели сегнетоалектрика.

а — антисегнетоэлектрик; б — нормальный сегнетовлектрик.

В промежут­ке имеются менее плотные цепочки, которые мы пока не будем рассматри­вать. Чтобы немного упростить наш анализ, предположим еще, что все ионы главной цепочки одинаковы. (Упроще­ние не очень значительное, потому что все важные эффекты еще останутся. Это просто одна из хитростей теорети­ческой физики. Сначала решают видо­измененную задачу, потому что так в первый раз ее легче понять, а затем, разобравшись, как все происходит, вносят все усложнения.)

Попробуем теперь выяснить, что будет происходить в нашей модели. Предположим, что дипольный момент каждого иона равен р, и пусть мы хотим вычислить поле вблизи одного из ионов в цепочке. Мы должны найти сумму полей от всех остальных ионов. Сначала вычислим поле от диполей только в одной вертикальной цепочке; об остальных цепочках поговорим поз­же. Поле на расстоянии r от диполя в направлении вдоль его оси дается формулой

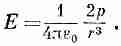
(11.32)

Для точки вблизи любого иона про­чие диполи, расположенные на одина­ковом расстоянии кверху и книзу от него, дают поля в одном и том же на­правлении, поэтому для всей цепочки получаем

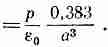
(11.33)

Не представляет большого труда пока­зать, что если бы наша модель была подобна кубическому кристаллу, т. е. если бы следующая идентичная линия проходила на расстоянии а, число 0,383 превратилось бы в 1/3 (~0,333). Другими словами, если бы соседние линии проходили на расстоянии а, они вносили бы в нашу сумму всего лишь —0,050. Однако следующая глав­ная цепочка, которую мы рассмотрим, находится на расстоянии 2а, и, как вы помните из гл. 7, поле, создаваемое периодической структурой, спадает с расстоянием экспоненциально. Поэтому эти линии вносят в сумму гораздо меньше —0,050, и мы можем просто пренебречь всеми остальными цепочками.

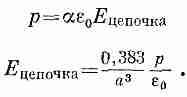
Теперь нужно выяснить, какова должна быть поляризуе­мость а, чтобы привести в действие механизм разгона. Предпо­ложим, что индуцированный момент р каждого атома цепочки в соответствии с уравнением (11.6) пропорционален действую­щему на него полю. Поляризующее поле, действующее на атом, мы получаем из Eцепочка с помощью формулы (11.32). Итак, мы имеем два уравнения:

Имеются два решения: когда Е и р оба равны нулю и когда Е и р не равны нулю, но при условии, что

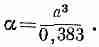
Таким образом, если a достигает величины a3/0,383, устанавли­вается постоянная поляризация, поддерживаемая своим соб­ственным полем. Это критическое равенство должно достигать­ся для титаната бария как раз при температуре Тс. (Заметьте, что если бы поляризуемость a была больше критического зна­чения для слабых полей, то она уменьшится при больших полях и в точке равновесия установится полученное нами ра­венство.)

Для ВаТiO3 промежуток a равен 2·10-8 см, поэтому мы должны ожидать значения a=21,8·10-24 см3. Мы можем сравнить эту величину с известными величинами поляризуе­мости отдельных атомов. Для кислорода a = 30,2·10-24 см3. (Мы на верном пути!) Но для титана a = 2,4·10-24см3. (Слиш­ком мало.) В нашей модели нам, видимо, следует взять среднее. (Мы могли бы рассчитать снова цепочку для перемежающихся атомов, но результат был бы почти такой же.) Итак, aсредн = 16,3·10-24 см3, что недостаточно велико для установ­ления постоянной поляризации.

Но подождите! Мы ведь до сих пор складывали только электронные поляризуемости. А есть еще и ионная поляриза­ция, возникающая из-за смещения иона титана. Однако по­требуется ионная поляризуемость величиной 9,2·10-24 см3.

(Более точное вычисление с учетом перемежающихся атомов показывает, что на самом деле требуется даже 11,9·10-24см3.) Чтобы понять свойства ВаТiO3, мы должны предположить, что возникает именно такая ионная поляризуемость.

Почему ион титана в титанате бария имеет столь большую ионную поляризуемость, неизвестно. Более того, непонятно, почему при меньших температурах он поляризуется одинаково хорошо и в направлении диагонали куба и в направлении диаго­нали грани. Если мы вычислим действительные размеры ша­риков на фиг. 11.9 и попробуем найти, достаточно ли свободно титан держится в коробке, образованной соседними атомами кислорода (а этого хотелось бы, потому что тогда его было бы легко сдвинуть), то получится совсем противоположный ответ. Он сидит очень плотно. Атомы бария держатся намного сво­боднее, но если считать, что это они движутся, то ничего не получится. Так что, как видите, вопрос совсем не ясен; остаются еще загадки, которые очень хотелось бы разгадать.

Возвращаясь к нашей простой модели (см. фиг. 11.10, а), мы видим, что поле от одной цепочки будет вызывать поляриза­цию соседней цепочки в противоположном направлении. Это значит, что, хотя каждая цепочка будет заморожена, постоян­ная поляризация в единице объема будет равна нулю! (Внешние электрические проявления тут не возникли бы, но можно было бы наблюдать определенные термодинамические эффекты.) Такие системы существуют и называются они антисегнетоэлектриками. Поэтому наше объяснение фактически относилось к антисегнетоэлектрикам. Однако в действительности титанат бария устроен очень похоже на то, что изображено на фиг. 11.10, б. Все кислородо-титановые цепочки поляризованы в одном направлении, потому что между ними помещаются проме­жуточные цепочки атомов. Хотя атомы в этих цепочках поляри­зованы не очень сильно и не очень тесно расположены, они все-таки будут немного поляризованы в направлении, антипараллельном кислородо-титановым цепочкам. Небольшие по­ля, создаваемые у следующей кислородо-титановой цепочки, заставят ее поляризоваться параллельно первой. Поэтому ВаТiO3 на самом деле сегнетоэлектрик, и произошло это бла­годаря атомам, находящимся в промежутке. Вы можете спро­сить: «А что же получается с прямым взаимодействием между двумя цепочками О — Ti?» Вспомним, однако, что прямое взаи­модействие убывает с расстоянием экспоненциально; действие цепочки из сильных диполей на расстоянии 2а может быть мень­ше действия цепочки слабых диполей на расстоянии а.

На этом мы закончим довольно подробное изложение наших сегодняшних познаний о диэлектрических свойствах газов, жидкостей и твердых тел.

* S?nger, Steiger, Gachter, Helvetica Physica Acta, 5, 200 (1932).

Имеется перевод: Ч. Киттель, «Введение в физику твердого те­ла», М., 1962.— Прим. ред.

*По-английски сегнетоэлектричество называется ferroelectricity (ферроэлектричество); этот термин возник по аналогии с ферромагнетизмом: наличие спонтанного момента (электрического в сегнетоэлектриках, магнитного в ферромагнетиках), точки Кюри, гистерезиса и т. п. Однако физическая природа этих групп явлений совершенно различ­на.— Прим. ред.