Глава 1 ЭЛЕКТРОМАГНЕТИЗМ

Глава 1

ЭЛЕКТРОМАГНЕТИЗМ

§1 .Электрические силы

§2. Электрические и магнитные поля

§3. Характеристики векторных полей

§4.Законы электро­магнетизма

§5.Что это такое— «поля»?

§6. Электромагнетизм в науке и технике

Повторить: гл. 12 (вып. 1) «Харак­теристики силы»

§ 1. Электрические силы

Рассмотрим силу, которая, подобно тяготе­нию, меняется обратно квадрату расстояния, но только в миллион биллионов биллионов биллионов раз более сильную. И которая от­личается еще в одном. Пусть существуют два сорта «вещества», которые можно назвать поло­жительным и отрицательным. Пусть одинако­вые сорта отталкиваются, а разные — притя­гиваются в отличие от тяготения, при котором происходит только притяжение. Что же тогда случится?

Все положительное оттолкнется со страш­ной силой и разлетится в разные стороны. Все отрицательное — тоже. Но совсем другое прои­зойдет, если положительное и отрицательное перемешать поровну. Тогда они с огромной силой притянутся друг к другу, и в итоге эти невероятные силы почти нацело сбалансируются, образуя плотные «мелкозернистые» смеси положительного и отрицательного; между двумя грудами таких смесей практически не будет ощущаться ни притяжения, ни отталкивания.

Такая сила существует: это электрическая сила. И все вещество является смесью положи­тельных протонов и отрицательных электронов, притягивающихся и отталкивающихся с неимо­верной силой. Однако баланс между ними столь совершенен, что, когда вы стоите возле кого-нибудь, вы не ощущаете никакого действия этой силы. А если бы баланс нарушился хоть немножко, вы бы это сразу почувствовали. Если бы в вашем теле или в теле вашего соседа (стоящего от вас на расстоянии вытянутой руки) электронов оказалось бы всего на 1% больше, чем протонов, то сила вашего отталкивания была бы невообразимо большой. Насколько большой? Доста­точной, чтобы поднять небоскреб? Больше! Достаточной, чтобы поднять гору Эверест? Больше! Силы отталкивания хватило бы, чтобы поднять «вес», равный весу нашей Земли!

Раз такие огромные силы в этих тонких смесях столь совер­шенно сбалансированы, то нетрудно понять, что вещество, стремясь удержать свои положительные и отрицательные заря­ды в тончайшем равновесии, должно обладать большой жестко­стью и прочностью. Верхушка небоскреба, скажем, отклоняется при порывах ветра лишь на пару метров, потому что электри­ческие силы удерживают каждый электрон и каждый протон более или менее на своих местах. А с другой стороны, если рас­смотреть достаточно малое количество вещества так, чтобы в нем насчитывалось лишь немного атомов, то там необязательно будет равное число положительных и отрицательных зарядов, и могут проявиться большие остаточные электрические силы. Даже если числа тех и других зарядов одинаковы, все равно между соседними областями может действовать значительная электрическая сила. Потому что силы, действующие между отдельными зарядами, изменяются обратно пропорционально квадратам расстояний между ними и может оказаться, что отрицательные заряды одной части вещества ближе к положи­тельным зарядам (другой части), чем к отрицательным. Силы притяжения тогда превзойдут силы отталкивания, и в итоге возникнет притяжение между двумя частями вещества, в кото­рых нет избыточного заряда. Сила, удерживающая атомы, и химические силы, скрепляющие между собой молекулы,— все это силы электрические, действующие там, где число зарядов неодинаково или где промежутки между ними малы.

Вы знаете, конечно, что в атоме имеются положительные протоны в ядре и электроны вне ядра. Вы можете спросить: «Если эти электрические силы так велики, то почему же про­тоны и электроны не налезают друг на друга? Если они стре­мятся образовать тесную компанию, почему бы ей не стать еще теснее?» Ответ связан с квантовыми эффектами. Если попы­таться заключить наши электроны в малый объем, окружающий протон, то, согласно принципу неопределенности, у них должен возникнуть средний квадратичный импульс, тем больший, чем сильнее мы их ограничим. Именно это движение (требуемое законами квантовой механики) мешает электрическому притяжению еще больше сблизить заряды.

Тут возникает другой вопрос: «Что скрепляет ядро?» В ядре имеется несколько протонов, и все они положительно заряжены. Почему же они не разлетаются? Оказывается, что в ядре, помимо электрических сил, еще действуют и неэлектрические силы, называемые ядерными. Эти силы более мощные, чем электриче­ские, и они способны, несмотря на электрическое отталкивание,

удержать протоны вместе. Действие ядерных сил, однако, про­стирается недалеко; оно падает гораздо быстрее, чем 1/r². И это приводит к важному результату. Если в ядре имеется слишком много протонов, то ядро становится чересчур большим и оно уже не может удержаться. Примером может служить уран с его 92 протонами. Ядерные силы действуют в основном между про­тоном (или нейтроном) и его ближайшим соседом, а электриче­ские силы действуют на большие расстояния и вызывают оттал­кивание каждого протона в ядре от всех остальных. Чем больше в ядре протонов, тем сильнее электрическое отталкивание, пока (как у урана) равновесие не станет столь шатким, что ядру почти ничего не стоит разлететься от действия электрического отталкивания. Стоит его чуть-чуть «толкнуть» (например, по­слав внутрь медленный нейтрон) — и оно разваливается надвое, на две положительно заряженные части, разлетающиеся врозь в результате электрического отталкивания. Энергия, которая при этом высвобождается,— это энергия атомной бомбы. Ее обычно именуют «ядерной» энергией, хотя на самом деле это «электрическая» энергия, высвобождаемая, как только электри­ческие силы превзойдут ядерные силы притяжения.

Наконец, можно спросить, чем скрепляется отрицательно заряженный электрон (ведь в нем нет ядерных сил)? Если элек­трон весь состоит из вещества одного сорта, то каждая его часть должна отталкивать остальные. Тогда почему же они не разле­таются в разные стороны? А точно ли существуют у электрона «части»? Может быть, следует считать электрон просто точкой и говорить, что электрические силы действуют только между разными точечными зарядами, так что электрон не действует сам на себя? Возможно. Единственно, что можно сейчас сказать,— что вопрос о том, чем скреплен электрон, вызвал много трудно­стей при попытке создать полную теорию электромагнетизма. И ответа на этот вопрос так и не получили. Мы займемся обсуж­дением его немного позже.

Как мы видели, можно надеяться, что сочетание электриче­ских сил и квантовомеханических эффектов определит структуру больших количеств вещества и, следовательно, их свойства. Одни материалы — твердые, другие — мягкие. Некоторые из них — электрические «проводники», потому что их электроны свободны и могут двигаться; другие — «изоляторы», их элек­троны привязаны каждый к своему атому. Позже мы выясним, откуда появляются такие свойства, но вопрос этот очень сложен, поэтому рассмотрим сначала электрические силы в самых про­стых ситуациях. Начнем с изучения одних только законов эле­ктричества, включив сюда и магнетизм, так как и то и другое в действительности суть явления одной и той же природы.

Мы сказали, что электрические силы, как и силы тяготения, уменьшаются обратно пропорционально квадрату расстояния между зарядами. Это соотношение называется законом Кулона. Однако этот закон перестает выполняться точно, если заряды движутся. Электрические силы зависят также сложным обра­зом и от движения зарядов. Одну из частей силы, действующей между движущимися зарядами, мы называем магнитной силой. На самом же деле это только одно из проявлений электрического действия. Потому мы и говорим об «электромагнетизме».

Существует важный общий принцип, позволяющий относи­тельно просто изучать электромагнитные силы. Мы обнаружи­ваем экспериментально, что сила, действующая, на отдельный заряд (независимо от того, сколько там еще есть зарядов или как они движутся), зависит только от положения этого отдель­ного заряда, от его скорости и величины. Силу F, действую­щую на заряд q,

движущийся со скоростью v, мы можем на­писать в виде:

(1.1)

здесь Е — электрическое поле в точке расположения заряда, а В — магнитное поле. Существенно, что электрические силы, действующие со стороны всех прочих зарядов Вселенной, скла­дываются и дают как раз эти два вектора. Значения их зависят от того, где находится заряд, и могут меняться со временем. Если мы заменим этот заряд другим, то сила, действующая на новый заряд, изменяется точно пропорционально величине заряда, если только все прочие заряды мира не меняют своего движения или положения. (В реальных условиях, конечно, каждый заряд действует на все прочие расположенные по со­седству заряды и может заставить их двигаться, так что иногда при замене одного данного заряда другим поля могут изме­ниться.)

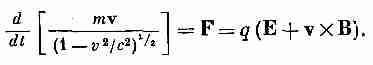
Из материала, изложенного в первом томе, мы знаем, как определить движение частицы, если сила, действующая на нее, известна. Уравнение (1.1) в сочетании с уравнением движения дает

(1.2)

Значит, если Е и В известны, то можно определить движение зарядов. Остается только узнать, как получаются Е и В.

Один из самых важных принципов, упрощающих получение величины полей, состоит в следующем. Пусть некоторое коли­чество движущихся каким-то образом зарядов создает поле E₁ , a другая совокупность зарядов — поле Е₂. Если действуют оба набора зарядов одновременно (сохраняя те же свои положения и движения, какими они обладали, когда рассматривались порознь), то возникающее поле рав­но в точности сумме

Е = Е₁ + Е₂. (1.3)

Этот факт называется принципом на­ложения полей (или принципом су­перпозиции}. Он выполняется и для магнитных полей.

Принцип этот означает, что если нам известен закон для электричес­кого и магнитного полей, образуемых одиночным зарядом, движущимся произвольным образом, то, значит, нам известны все законы электроди­намики. Если мы хотим знать силу, действующую на заряд А, нам нужно только рассчитать величину полей Е и В, созданных каждым из зарядов В, С, D и т. д., и сложить все эти Е и В; тем самым мы найдем поля, а из них — силы, действующие на А. Если бы оказалось, что поле, созда­ваемое одиночным зарядом, отлича­ется простотой, то это стало бы са­мым изящным способом описания законов электродинамики. Но мы уже описывали этот закон (см. вып. 3, гл. 28), и, к сожалению, он довольно сложен.

Оказывается, что форма, в которой законы электродинамики становятся простыми, совсем не такая, какой можно было бы ожидать. Она не проста, если мы захотим иметь формулу для силы, с которой один заряд действует на другой. Правда, когда заряды покоятся, закон силы — закон Кулона — прост, но когда заряды движутся, соотношения усложняются из-за запа­здывания во времени, влияния ускорения и т. п. В итоге лучше не пытаться строить электродинамику с помощью одних лишь законов сил, действующих между зарядами; гораздо более приемлема другая точка зрения, при которой с законами элек­тродинамики легче управляться.

§ 2. Электрические и магнитные поля

Первым делом нужно несколько расширить наши представ­ления об электрическом и магнитном векторах Е и В. Мы опре­делили их через силы, действующие на заряд. Теперь мы наме­реваемся говорить об электрическом и магнитном полях в точке, даже если там нет никакого заряда.

Фиг. 1.1. Векторное поле, пред­ставленное множеством стрелок, длина и направление которых от­мечают величину векторного поля в тех точках, откуда выходят стрелки.

Следовательно, мы утверж­даем, что раз на заряд «действуют» силы, то в том месте, где он стоял, остается «нечто» и тогда, когда заряд оттуда убрали. Если заряд, расположенный в точке (х, у, z), в момент t ощущает действие силы F, согласно уравнению (1.1), то мы связываем векторы Е и В с точкой (х, у, z) в пространстве. Можно считать, что Е (х, y, z, t) и В (х, у, z, t) дают силы, действие которых ощутит в момент t заряд, расположенный в (х, у, z), при условии, что помещение заряда в этой точке не потревожит ни распо­ложения, ни движения всех прочих зарядов, ответственных за поля.

Следуя этому представлению, мы связываем с каждой точкой (х, у, z) пространства два вектора Е и В, способных меняться со временем. Электрические и магнитные поля тогда рассматри­ваются как векторные функции от х, у, z и t. Поскольку вектор определяется своими компонентами, то каждое из полей Е (х, у, 2, t) и В (х, у, z, t) представляет собой три математиче­ские функции от х, у, z и t.

Именно потому, что Е (или В) может быть определено для каждой точки пространства, его и называют «полем». Поле — это любая физическая величина, которая в разных точках про­странства принимает различные значения. Скажем, темпера­тура — это поле (в этом случае скалярное), которое можно записать в виде Т (х, у, z). Кроме того, температура может ме­няться и во времени, тогда мы скажем, что температурное поле зависит от времени, и напишем Т (х, у, z, t). Другим примером поля может служить «поле скоростей» текущей жидкости. Мы записываем скорость жидкости в любой точке пространства в момент t в виде v (х, у, z, t). Поле это векторное.

Вернемся к электромагнитным полям. Хотя формулы, по которым они создаются зарядами, и сложны, у них есть следую­щее важное свойство: связь между значениями полей в некото­рой точке и значениями их в соседней точке очень проста. Нескольких таких соотношений (в форме дифференциальных уравнений) достаточно, чтобы полностью описать поля. Именно в такой форме законы электродинамики и выглядят особенно просто.

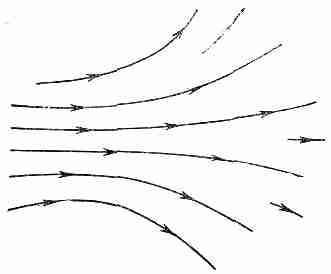
Фиг. 1.2. Векторное поле, пред­ставленное линиями, касательны­ми к направлению векторного поля в каждой точке.

Плотность линий указывает величину вектора поля.

Немало изобретательности было потрачено на то, чтобы помочь людям мысленно представить поведение полей. И самая правильная точка зрения — это самая отвлеченная: надо про­сто рассматривать поля как математические функции коорди­нат и времени. Можно также попытаться получить мысленную картину поля, начертив во многих точках пространства по век­тору так, чтобы каждый из них показывал напряженность и направление поля в этой точке. Такое представление приво­дится на фиг. 1.1. Можно пойти и дальше: начертить линии, которые в любой точке будут касательными к этим векторам. Они как бы следуют за стрелками я сохраняют направление поля. Если это сделать, то сведения о длинах векторов будут утеряны, но их можно сохранить, если в тех местах, где напря­женность поля мала, провести линии пореже, а где велика — погуще. Договоримся, что число линий на единицу площади, расположенной поперек линий, будет пропорционально на­пряженности поля. Это, конечно, всего лишь приближение; иногда нам придется добавлять новые линии, чтобы их коли­чество отвечало напряженности поля. Поле, изображенное на фиг. 1.1, представлено линиями поля на фиг. 1.2.

§ 3. Характеристики векторных полей

Векторные поля обладают двумя математически важными свойствами, которыми мы будем пользоваться при описании законов электричества с полевой точки зрения. Представим себе замкнутую поверхность и зададим вопрос, вытекает ли из нее «нечто», т. е. обладает ли поле свойством «истечения»? Скажем, для поля скоростей мы можем поинтересоваться, всегда ли скорость направлена от поверхности, или, в более общем слу­чае, вытекает ли из поверхности больше жидкости (в единицу времени), нежели втекает.

Фиг. 1.3. Поток векторного поля через поверхность, определяе­мый как произведение среднего зна­чения перпендикулярной состав­ляющей вектора на площадь этой поверхности.

Общее количество жидкости, выте­кающее через поверхность, мы назовем «потоком скорости» через поверхность за единицу времени. Поток через элемент поверхности равен составляющей скорости, перпендикулярной к элементу, умноженной на его площадь. Для произвольной замкнутой поверхности суммар­ный поток равен среднему зна­чению нормальной компоненты скорости (отсчитываемой нару­жу), умноженному на площадь поверхности:

Поток = (Средняя нормальная ком­понента)·(Площадь поверхности).

(1.4)

В случае электрического поля можно математически определить понятие, сходное с истоком жидкости; мы тоже

Фиг. 1.4. Поле скоростей в жид­кости (а).

Представьте себе трубку постоянного се­чения, уложенную вдоль произвольной замкнутой кривой (б). Если жидкость внезапно заморозить повсюду, кроме трубки, то жидкость в трубке начнет циркулировать (в).

Фиг. 1.5. Циркуляция векторного поля, равная произведению

средней касательной составляющей вектора (с учетом ее знака

по отношению к направлению обхода) на длину контура.

называем его потоком, но, конечно, это уже не течение какой-то жидкости, потому что электрическое поле нельзя считать ско­ростью чего-то. Оказывается все же, что математическая вели­чина, определяемая как средняя нормальная компонента поля, по-прежнему имеет полезное значение. Тогда мы говорим о потоке электричества, также определяемом уравнением (1.4). Наконец, полезно говорить и о потоке не только сквозь замкну­тую, но и сквозь любую ограниченную поверхность. Как и прежде, поток сквозь такую поверхность определяется как средняя нормальная компонента вектора, умноженная на пло­щадь поверхности. Эти представления иллюстрируются фиг. 1.3. Другое свойство векторных полей касается не столько по­верхностей, сколько линий. Представим опять поле скоростей, описывающее поток жидкости. Можно задать интересный вопрос: циркулирует ли жидкость? Это значит: существует ли вращательное ее движение вдоль некоторого замкнутого кон­тура (петли)? Вообразите себе, что мы мгновенно заморозили жидкость повсюду, за исключением внутренней части замкну­той в виде петли трубки постоянного сечения (фиг. 1.4). Снаружи трубки жидкость остановится, но внутри она может продолжать двигаться, если в ней (в жидкости) сохранился импульс, т. е. если импульс, который гонит ее в одном направлении, больше импульса в обратном. Мы определяем величину, называемую циркуляцией, как скорость жидкости в трубке, умноженную на длину трубки. Опять-таки мы можем расширить наши пред­ставления и определить «циркуляцию» для любого векторного поля (даже если там нет ничего движущегося). У всякого век­торного поля циркуляция по любому воображаемому замкнутому контуру определяется как средняя касательная компонента вектора (с учетом направления обхода), умноженная на про­тяженность контура (фиг. 1.5):

Циркуляция = (Средняя касательная компонента)·(Длина пути обхода). (1.5)

Вы видите, что это определение действительно дает число, про­порциональное циркуляции скорости в трубке, просверленной в быстрозамороженной жидкости.

Пользуясь только этими двумя понятиями — понятием о потоке и понятием о циркуляции,— мы способны описать все законы электричества и магнетизма. Вам, быть может, трудно будет отчетливо понять значение законов, но они дадут вам некоторое представление о том, каким способом в конечном счете может быть описана физика электромагнитных явлений.

§ 4. Законы электромагнетизма

Первый закон электромагнетизма описывает поток электри­ческого поля:

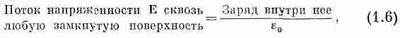
где e₀ — некоторая постоянная (читается эпсилон-нуль). Если внутри поверхности нет зарядов, а вне ее (даже совсем рядом) есть, то все равно средняя нормальная компонента Е равна нулю, так что никакого потока через поверхность нет. Чтобы показать пользу от такого типа утверждений, мы дока­жем, что уравнение (1.6) совпадает с законом Кулона, если только учесть, что поле отдельного заряда обязано быть сфери­чески симметричным. Проведем вокруг точечного заряда сферу. Тогда средняя нормальная компонента в точности равна значе­нию Е в любой точке, потому что поле должно быть направлено по радиусу и иметь одну и ту же величину во всех точках сферы. Тогда наше правило утверждает, что поле на поверхности сферы, умноженное на площадь сферы (т. е. вытекающий из сферы поток), пропорционально заряду внутри нее. Если увеличивать радиус сферы, то ее площадь растет, как квадрат радиуса. Произведение средней нормальной компоненты электрического поля на эту площадь должно по-прежнему быть равно внутрен­нему заряду, значит, поле должно убывать, как квадрат рас­стояния; так получается поле «обратных квадратов».

Если взять в пространстве произвольную кривую и измерить циркуляцию электрического поля вдоль этой кривой, то ока­жется, что она в общем случае не равна нулю (хотя в кулоновом поле это так). Вместо этого для электричества справедлив вто­рой закон, утверждающий, что

И, наконец, формулировка законов электромагнитного поля будет закончена, если написать два соответствующих уравнения для магнитного поля В:

(1.8)

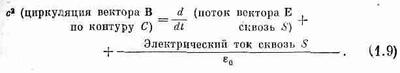
А для поверхности S, ограниченной кривой С:

Появившаяся в уравнении (1.9) постоянная с² — это квадрат скорости света. Ее появление оправдано тем, что магнетизм по существу есть релятивистское проявление электричества. А константа e_о поставлена для того, чтобы возникли привычные единицы силы электрического тока.

Уравнения (1.6) — (1.9), а также уравнение (1.1) — это все законы электродинамики.

Как вы помните, законы Нью­тона написать было очень просто, но из них зато вытекало мно­жество сложных следствий, так что понадобилось немало времени, чтобы изучить их все. Законы электромагнетизма написать несравненно трудней, и мы должны ожидать, что следствия из них будут намного более запутаны, и теперь нам придется очень долго в них разбираться.

Мы можем проиллюстрировать некоторые законы электро­динамики серией несложных опытов, которые смогут нам пока­зать хотя бы качественно взаимоотношения электрического и магнитного полей. С первым членом в уравнении (1.1) вы зна­комитесь, расчесывая себе волосы, так что о нем мы говорить не будем. Второй член в уравнении (1.1) можно продемонстриро­вать, пропустив ток по проволоке, висящей над магнитным бруском, как показано на фиг. 1.6. При включении тока про­волока сдвигается из-за того, что на нее действует сила F=qvXB. Когда по проводу идет ток, заряды внутри него движутся, т. е. имеют скорость v, и на них действует магнит­ное поле магнита, в результате чего провод отходит в сторону.

Когда провод сдвигается влево, можно ожидать, что сам магнит испытает толчок вправо. (Иначе все это устройство можно было бы водрузить на платформу и получить реактивную систему, в которой импульс не сохранялся бы!) Хотя сила чересчур мала, чтобы можно было заметить движение магнитной палочки, однако движение более чувствительного устройства, скажем стрелки компаса, вполне заметно.

Каким же образом ток в проводе толкает магнит? Ток, теку­щий по проводу, создает вокруг него свое собственное магнит­ное поле, которое и действует на магнит. В соответствии с по­следним членом в уравнении (1.9) ток должен приводить к цир­куляции вектора В; в нашем случае линии поля В замкнуты вокруг провода, как показано на фиг. 1.7. Именно это поле В и ответственно за силу, действующую на магнит.

Фиг.1.6.Магнитная палочка, создающая возле провода поле В.

Когда по проводу идет ток, провод смещается из-за действия силы F = qvXB.

Уравнение (1.9) сообщает нам, что при данной величине тока, текущего по проводу, циркуляция поля В одинакова для любой кривой, окружающей провод. У тех кривых (окружно­стей, например), которые лежат далеко от провода, длина ока­зывается больше, так что касательная компонента В должна убывать. Вы видите, что следует ожидать линейного убывания В с удалением от длинного прямого провода.

Мы сказали, что ток, текущий по проводу, образует вокруг него магнитное поле и что если имеется магнитное поле, то оно действует с некоторой силой на провод, по которому идет ток.

Фиг.1.7. Магнитное поле тока, текущего по про­воду, действует на магнит с некоторой силой.

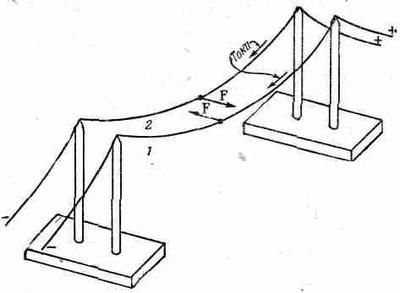
Фиг. 1.8. Два провода, по которым течет ток,

тоже действуют друг на друга с определенной силой.

Значит, следует думать, что если магнитное поле будет создано током, текущим в одном проводе, то оно будет действовать с не­которой силой и на другой провод, по которому тоже идет ток. Это можно показать, применив два свободно подвешенных про­вода (фиг. 1.8). Когда направление токов одинаково, провода притягиваются, а когда направления противоположны — от­талкиваются.

Короче говоря, электрические токи, как и магниты, создают магнитные поля. Но тогда что же такое магнит? Раз магнитные поля создаются движущимися зарядами, то не может ли ока­заться, что магнитное поле, созданное куском железа, на самом деле есть результат действия токов? Видимо, так оно и есть. В наших опытах можно заменить магнитную палочку катушкой с навитой проволокой, как показано на фиг. 1.9. Когда ток проходит по катушке (как и по прямому проводу над нею), наблюдается точно такое же движение проводника, как и преж­де, когда вместо катушки стоял магнит. Все выглядит так, как если бы внутри куска железа непрерывно циркулировал ток. Действительно, свойства магнитов можно понять как непре­рывный ток внутри атомов железа. Сила, действующая на маг­нит на фиг. 1.7, объясняется вторым членом в уравнении (1.1).

Откуда же берутся эти токи? Один источник — это движе­ние электронов по атомным орбитам. У железа это не так, но у некоторых материалов происхождение магнетизма именно таково. Кроме вращения вокруг ядра атома, электрон вращается еще вокруг своей собственной оси (что-то похожее на вращение Земли); вот от этого-то вращения и возникает ток, создающий магнитное поле железа. (Мы сказали «что-то похожее на вра­щение Земли», потому что на самом деле в квантовой механике вопрос столь глубок, что не укладывается достаточно хорошо в классические представления.) В большинстве веществ часть электронов вертится в одну сторону, другая — в другую, так что магнетизм исчезает, а в железе (по таинственной причине, о которой мы поговорим позже) многие электроны вращаются так, что их оси смотрят в одну сторону и это служит источником магнетизма.

Поскольку поля магнитов порождаются токами, то в урав­нения (1.8) и (1.9) нет нужды вставлять добавочные члены, учитывающие существование магнитов. В этих уравнениях речь идет обо всех токах, включая круговые токи от вращающихся электронов, и закон оказывается правильным. Надо еще отме­тить, что, согласно уравнению (1.8), магнитных зарядов, по­добных электрическим зарядам, стоящим в правой части урав­нения (1.6), не существует. Они никогда не были обнаружены.

Первый член в правой части уравнения (1.9) был открыт Максвеллом теоретически; он очень важен. Он говорит, что изменение электрических полей вызывает магнитные явления. На самом деле без этого члена уравнение утеряло бы смысл, ведь без него исчезли бы токи в незамкнутых контурах. А на деле такие токи существуют; об этом говорит следующий при­мер. Представьте конденсатор, составленный из двух плоских пластин.

Фиг. 1.9. Магнитная палочка, показанная на фиг. 1.6,

может быть заменена катушкой, по которой течет

ток.

На провод по-прежнему будет действовать сила.

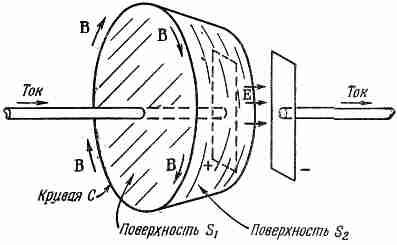
Фиг. 1.10. Циркуляция поля В по кривой С опре­деляется либо током, текущим сквозь поверх­ность S₁ либо быстро­той изменения потока, поля Е сквозь поверх­ность S₂.

Он заряжается током, притекающим к одной из пла­стин и оттекающим от другой, как показано на фиг. 1.10. Про­ведем вокруг одного из проводов кривую С и натянем на нее поверхность (поверхность S₁, которая пересечет провод. В со­ответствии с уравнением (1.9) циркуляция поля В по кривой С дается величиной тока в проводе (умноженной на с²). Но что будет, если мы натянем на кривую другую поверхность S₂ в форме чашки, донышко которой расположено между пласти­нами конденсатора и не касается провода? Через такую поверх­ность никакой ток, конечно, не проходит. Но ведь простое изме­нение положения и формы воображаемой поверхности не должно изменять реального магнитного поля! Циркуляция поля В должна остаться прежней. И действительно, первый член в пра­вой части уравнения (1.9) так комбинируется со вторым членом, что для обеих поверхностей S₁ и S₂возникает одинаковый эффект. Для S₂циркуляция вектора В выражается через сте­пень изменения потока вектора Е от одной пластины к другой. И получается, что изменение Е связано с током как раз так, что уравнение (1.9) оказывается выполненным. Максвелл видел необходимость этого и был первым, кто написал полное урав­нение.

С помощью устройства, изображенного на фиг. 1.6, можно продемонстрировать другой закон электромагнетизма. Отсо­единим концы висящей проволочки от батарейки и присоединим их к гальванометру — прибору, регистрирующему прохожде­ние тока по проводу. Стоит лишь в поле магнита качнуть про­волоку, как по ней сразу пойдет ток. Это новое следствие урав­нения (1.1): электроны в проводе почувствуют действие силы F=qvXB. Скорость их сейчас направлена в сторону, потому что они отклоняются вместе с проволочкой. Это v вместе с вер­тикально направленным полем В магнита приводит к силе, действующей на электроны вдоль провода, и электроны отправ­ляются к гальванометру.