ЗВУЧАНИЕ КРИСТАЛЛА

ЗВУЧАНИЕ КРИСТАЛЛА

Летом 1924 г. академик Абрам Федорович Иоффе получил письмо из Лейдена от своего друга — выдающегося физика-теоретика Пауля Эренфеста. В этом письме сообщалось, что Пауль Эренфест собирается приехать к Иоффе в гости где-то в августе — сентябре. В конце письма — совсем неожиданная просьба: рафинированный физик-теоретик, тончайший ценитель формальной строгости теоретических построений новой физики просит организовать ему возможность принять участие в не очень сложной экспериментальной работе. Что-нибудь с кристаллами.

Я не могу толково объяснить читателю, чем эта просьба была вызвана. Быть может, обычная «охота к перемене мест», желание увидеть любимую науку с иной позиции, быть может, попытка поиска иного поприща: Эренфест был болезненно самокритичен и очень скептически относился к своим достижениям в теоретической физике. Так или иначе, но в августе — сентябре 1924 г. Иоффе и Эренфест «в четыре руки» занимались исследованиями пластического деформирования монокристаллов цинка. Они заметили, что деформирование монокристаллов осуществляется скачкообразно и что скачки сопровождаются потрескиванием. Выражаясь научно, скажем так: пластическое деформирование сопровождается акустической эмиссией.

Где-то я встречал разумную мысль о том, что это очень интересное явление следовало бы именовать «эффект Иоффе — Эренфеста». В Ленинградском физико-техническом институте он очень подробно исследовался ученицей А. Ф. Иоффе Мариной Викторовной Классен-Неклюдовой, ныне известным профессором-кристаллофизиком.

Собственно, и до Иоффе и Эренфеста звучание кристалла слышали неоднократно. Все паяльщики и лудильщики издавна знают, что при деформировании третник (сплав: 1 часть свинца и 2 части олова) потрескивает. Но в данном случае, как и в несметном количестве подобных, важно не то, что кто-то видел физическое явление, а то, что кто-то иной обратил на него внимание, понял его важность, а это и значит — сделал открытие.

Итак, при деформировании кристалл может звучать. Возникает большое количество совсем не риторических вопросов. Почему возникает звук? Почему он подобен не гулу сирены, а тиканью часов. В Ленинградском физико-техническом институте об образцах Иоффе и Эренфеста говорили: цинковые часы. И еще: нельзя ли повлиять на это звучание? Нельзя ли его использовать, дать ему выход в практику?

Будем разбираться в сформулированных вопросах, так сказать, в порядке их поступления.

Начнем с сотворения модели явления, с поисков аналогий, которые могли бы помочь ответить на интересующие нас вопросы. Вспомним, что пластическая деформация сопровождается движением дислокаций. Естественно предположить, что звучание кристалла и движение в нем дислокаций — явления не независимые. Тем более, что сразу же напрашивается аналогия: движение пули в воздухе сопровождается «акустической эмиссией», или, попросту говоря, свистом. С пулей и воздухом все ясно: в пуле, имеющей массу m и летящей со скоростью ?, запасена кинетическая энергия, та самая, которая, как известно, равна m?²/2. Постепенно теряя эту энергию на преодоление сопротивления воздуха, пуля возбуждает в нем упругие волны, которые нашим ухом воспринимаются, как свист. Для того чтобы задуманная нами аналогия оказалась состоятельной, нам нужно подобно массе пули представить себе массу дислокации — величину не совсем обычную. Измерять ее в граммах нельзя, видимо, ее следует измерять в граммах на единицу длины линии дислокации. Без доказательств сообщу читателю, что эта величина определяется произведением плотности вещества кристалла d на квадрат вектора Бюргерса: db². Эта формула не должна вызвать подозрений, все в ней разумно: присутствует и характеристика кристалла (в виде плотности вещества), и характеристика дислокации в виде вектора Бюргерса, который входит в квадрате, символизирующем физически оправданную независимость массы дислокации единичной длины от того, как ориентирован ее вектор Бюргерса. Если бы вектор Бюргерса в формулу, определяющую массу дислокации, входил в первой степени, изменение его ориентации на противоположное меняло бы знак массы, т. е. она могла бы стать отрицательной, что нелепо! Итак, кинетическую энергию дислокации единичной длины можно записать в виде W_?= db²?²/2. А дальше все, как с пулей: дислокация движется в кристалле, теряет свою кинетическую энергию, эта энергия переходит в энергию упругих волн в кристалле, и кристалл звучит. Все ясно!

Здесь, пожалуй, рассуждения «по аналогии» следует прервать. Дальше опасно, легко можно заблудиться. Ну, например, летящая пуля свистит непрерывно, а при пластическом деформировании слышатся потрескивания. Удовлетворимся тем, что аналогия помогла нам понять основное: движущаяся в кристалле дислокация возмущает решетку, передает ей часть своей энергии, в решетке возбуждаются упругие волны, т. е. звук.

Имея в виду описанный дислокационный механизм, можно понять и причину прерывистого звучания. Дело в том, что тот непрерывный свист, который издает летящая пуля, видимо, издает и дислокация. Этот слабый звук наше ухо просто не улавливает. Но вот в момент, когда дислокация выходит за пределы кристалла и когда вместе с ее исчезновением скачкообразно выделяется вся принадлежащая ей кинетическая энергия (подчеркнем: не постепенно передается решетке, а скачкообразно, сполна), мы слышим резкий щелчок. У физиков, занимающихся акустической эмиссией кристаллов, есть специальный термин — «переходное излучение». Оно возникает, когда дислокация переходит из среды с одной плотностью в среду с другой плотностью. Это значит, что скачкообразно меняется масса дислокации, следовательно, и ее кинетическая энергия и, следовательно, должен прозвучать щелчок. Здесь, пожалуй, следует заметить, что термин «переходное излучение» теорией акустической эмиссии кристаллов был заимствован из электродинамики, той ее главы, которая посвящена движению заряда в среде. Пересекая границу между двумя средами, заряд излучает так называемое «переходное излучение».

Можно указать большое количество реальных ситуаций, при которых исчезающая дислокация (или дислокации) должна издавать щелчок. Ну, скажем, с некоторой скоростью навстречу друг другу в одной плоскости скольжения движутся две дислокации с противоположно ориентированными векторами Бюргерса. При встрече такие дислокации исчезают, аннигилируют, при этом выделяется энергия, равная сумме кинетических энергий обеих дислокаций. Если скорости движения дислокаций были не малы, то выделяющаяся при этом энергия может оказаться значительной. Если, например, ?_? ? 10^-1 ?_зв ? 10⁴ см/с, то в металлах, где d ? 10 г/см³, величина W_? ? 5^.10^-6 эрг/см.

Может произойти и по-другому: кольцевая дислокационная линия (дислокационная петля) будет стягиваться в точку, следовательно, уменьшать свою длину, выделять энергию и возбуждать звук. Может быть и так: в процессе пластического деформирования дислокация сорвется с затормозивших ее стопоров и скачкообразно начнет двигаться, издавая при этом звук.

Мы интересовались, нельзя ли повлиять на звучание деформируемого кристалла. Конечно же, можно. Надо предварительно каким-либо способом ввести в кристалл дислокации, а затем, планомерно деформируя его, привести их в движение.

Нам осталось два дела. Во-первых, рассказать о том, как физики экспериментально исследуют звучание кристалла, обусловленное движением дислокаций, и, во-вторых, о том, как можно этот эффект использовать практически.

Экспериментальных работ по акустической эмиссии кристаллов, обусловленной дислокациями, очень не много. Я расскажу лишь об одном опыте, о том, который мне и понравился больше иных, и вызвал полное к себе доверие. Поставлен он был харьковскими кристаллофизиками В. С. Бойко, Р. И. Гарбером и их сотрудниками. Авторы этого опыта воспользовались тем, что во многих кристаллах, в частности и кристалле кальцита, с которым они и экспериментировали, под влиянием извне приложенной сосредоточенной нагрузки (ее можно создать нажатием на лезвие клина, касающегося поверхности кристалла) получаются скопления большого количества однотипных дислокаций.

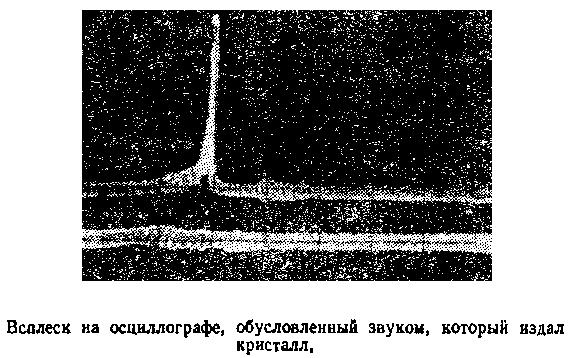
Они образуют стенку, концы которой касаются поверхности кристалла. При снятии внешней нагрузки эти скопления покидают кристалл, с большой скоростью дислокации выходят за его пределы. Акт выхода сопровождается сильной акустической эмиссией. Возникающий звуковой сигнал очень четко можно зарегистрировать осциллографом. Для того чтобы не принять желаемое за действительное, авторы опыта с помощью скоростной кинокамеры следили за выходом дислокаций. Момент выхода дислокаций и момент всплеска звука совпали. Убедительный опыт!

Теперь о практических приложениях, точнее, об одном из них, очень важном и очень красивом. В 1959 г. немецкий физик Кайзер, изучая акустическую эмиссию металлов, обнаружил, что, если образец, который под влиянием определенной внешней нагрузки звучал, освободить от этой нагрузки, а потом повторно нагрузить, он зазвучит лишь при условии, если повторная нагрузка превзойдет начальную. В физической литературе это явление именуется «эффект Кайзера». Зная о нем, представьте себе, что некоторый полый сосуд мы герметически закроем металлической мембраной и опустим его в море на некоторую глубину, где к мембране будет приложено напряжение, обусловленное гидростатическим давлением,

?_h = dgh,

(d — плотность воды, g — ускорение свободного падения, h — глубина погружения). В воде, согласно Кайзеру, мембрана «вызвучит» все, что должна «вызвучать» при напряжении ?_h. После извлечения из воды ее следует вынудить начать звучать под влиянием внешней, точно измеряемой нагрузки ?* > ?_h . Этим самым мы узнаем у мембраны, на какой глубине она находилась. Очевидно, на глубине h = ?*/dg. Таким образом, способность кристалла издавать звуки может быть использована для создания глубиномеров. Я рассказал лишь об общей идее, на которой основан акустический глубиномер. При ее осуществлении возникает много трудностей и ограничений. Трудности преодолеваются, ограничения учитываются.