В КРИСТАЛЛЕ ВОЗНИКАЕТ ТРЕЩИНА
В КРИСТАЛЛЕ ВОЗНИКАЕТ ТРЕЩИНА
Понятия «трещина», «треснуло» настолько будничны, что кажутся само собой разумеющимися. Треснуло — значит появилась трещина! Появилась трещина — значит треснуло! Между тем трещина заслуживает и, по праву, требует пристального внимания к себе. Ведь только что мы сформулировали сентенцию: «треснуло — значит появилась трещина». А с этим не могут мириться ни конструкторы, создающие машины, ни машины, работающие по замыслу конструкторов.
Итак, о том, как в кристалле поселяется трещина. Возможностей поселить в себе трещину у кристалла — множество! Я хочу рассказать о двух механизмах возникновения трещины в кристалле. О тех, которые отличаются наглядностью и оказываются действующими во многих реальных ситуациях.
Вначале одно общее соображение. Кристаллы под влиянием приложенных к ним усилий должны деформироваться. Если возникающие в кристалле напряжения достаточно велики, его деформация со временем будет нарастать. Хочется сказать: кристалл будет «течь». Так вот, если кристаллу ничто не мешает свободно «течь», он и будет «течь», сохраняя сплошность, а если свободно течь ему нечто мешает, в нем под влиянием нагрузки может возникнуть трещина! Соображение общее, и поэтому такие расплывчатые слова, как «ничто» и «нечто», не должны вызывать протеста. Говоря о течении кристалла, я имею в виду, что под влиянием приложенной нагрузки со временем его деформация нарастает, как, скажем, это могло бы происходить с нагретой до высокой температуры стеклянной нитью, к которой подвешен груз. Сейчас важны не конкретные детали, а общая мысль о том, что трещина может возникнуть, если свободная деформация кристалла, его течение почему-либо запрещено. Только эта мысль!
Теперь о двух конкретных механизмах возникновения трещин. Один из них был понят и описан английским ученым Стро и очень скоро вошел в плоть науки о реальном кристалле. Так бывает часто: ранее неизвестное со временем (и иной раз очень скоро!) кажется само собой разумеющимся. Говорят, что новая идея последовательно вызывает две реакции: вначале — «этого не может быть!», а затем — «иначе и быть не может!». Пожалуй, именно такая судьба оказалась и у идеи механизма появления трещины «по Стро». Вот посудите сами.
Помните очерк о движении дислокаций в плоскости скольжения и аналогию между дислокациями движущимися одна за другой, и цепочкой туристов, идущих по тропке? Если температура кристалла высока, дислокации, остановившиеся перед непреодолимым стопором, диффузионно обходят его. А если температура невысока и, следовательно, диффузионная подвижность атомов мала, вблизи стопора будет происходить иное: головная дислокация у стопора остановится, движущаяся за ней приблизится на расстояние, немного меньшее того, которое было между этими дислокациями, когда они скользили беспрепятственно. Головная дислокация испытает при этом давление. Со временем оно будет нарастать по мере приближения последующих дислокаций цепочки. Если у препятствия затормозится ряд следующих друг за другом п дислокаций, головная дислокация будет испытывать на себе напряжение, n-кратно превосходящее внешнее, то, которое вынуждает дислокации скользить. Оно может оказаться настолько большим, что превзойдет прочность кристалла, сдерживающего напор дислокаций, и вблизи кристалла зародится клиновидная трещина. Она появится вследствие объединения ближайших к стопору дислокаций. Следующие дислокации как-бы проваливаются в зародившуюся трещину, и она подрастает. Пока дислокация скользила свободно, кристалл «тек», а когда встретился стопор и движение дислокаций затормозилось, появилась трещина. Все как и следовало из «общего соображения».
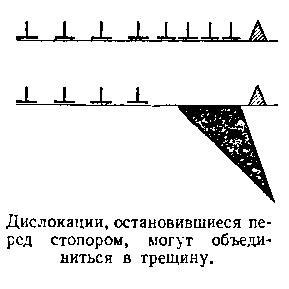
О трещине, возникшей «по Стро», следует кое-что рассказать. Во-первых, ее ширина будет тем больше, чем большее число дислокаций, объединившись, приняло участие в ее формировании. Если это число обозначить п, то ширина трещины будет равна пb, где b — вектор Бюргерса. О такой трещине иногда говорят так: дислокация с Еектором Бюргерса пb. Во-вторых, оказывается, что направление трещины с направлением плоскости скольжения образует угол, близкий к 70°. Не стану приводить расчеты, из которых эта величина следует, а лучше предложу читателю убедиться в правильности утверждения, проделав опыт с моделью кристалла в виде листа белой бумаги. Впервые мне его продемонстрировал профессор Е. Д. Щукин и подарил для этой книги две фотографии, иллюстрирующие последовательные этапы опыта, который он производил, так сказать, собственноручно.
Опыт прост. На листе белой бумаги нужно карандашом провести прямую линию — символ полосы скольжения. Затем на некотором ограниченном участке этой линии бритвой сделать в бумаге разрез. Именно вдоль него можно будет осуществить сдвиг, символизирующий результат скольжения дислокаций. Концы разреза — символы стопоров, далее которых сдвиг не смог и не сможет распространяться. А теперь лист следует положить на гладкий стол, прижать его к столу двумя руками, расположенными с двух сторон от карандашной линии, и, медленно сдвигая руки в противоположных направлениях, спровоцировать сдвиг. При этом бумага, разумеется, прорвется, но не вдоль карандашной линии, а в направлении, образующем с карандашной линией угол, близкий к 70°!
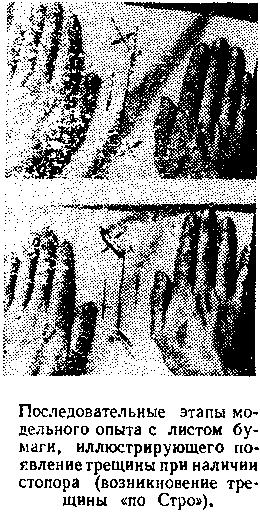
Посоветовав читателю сделать этот модельный опыт, я, разумеется, ничего ему не пояснил. Быть может, лишь помог возникновению интуитивного восприятия правильности одного из следствий теории Стро. А это, пожалуй, не так уж мало. Я тешу себя мыслью, что от модельного опыта, а заодно и от автора популярного изложения большего можно и не требовать.
Механизм «по Стро» — не просто правдоподобный вымысел теоретика. Этот механизм реально действует, особенно в тех случаях, когда деформируется кристаллическое тело, пересеченное множеством границ раздела между элементами его структуры. Граница обычно играет роль стопора, и вблизи нее возникает трещина.
Все рассказанное о механизме возникновения трещины «по Стро» дает основание для важного замечания. Почему, собственно, кристалл «согласился» поселить в себе трещину? А потому, что, образовав ее, дислокации, скопившиеся перед стопором, освободились от действующих на них сил. Вообще говоря, есть, например, уже обсуждавшаяся нами возможность диффузионно обойти препятствие и переместиться в другую плоскость скольжения над или под препятствием, как бы обойти его, а затем скользить в этой другой плоскости, где стопора нет. Напомним еще раз, что при низкой температуре этот процесс не может происходить! Это одна из причин того, что при низкой температуре кристаллы хрупки, а при высокой — пластичны.
На этом, пожалуй, можно окончить рассказ о механизме появления трещины «по Стро» и перейти к рассказу о механизме «по Коттреллу». Коттрелл — английский физик-теоретик.
Механизм «по Коттреллу» от механизма «по Стро» отличается лишь образом стопора, который тормозит свободное скольжение дислокаций. В механизме Коттрелла в роли стопора, тормозящего движение цепочки дислокаций вдоль данного направления скольжения, оказываются такие же дислокации, которые, однако, движутся вдоль другого направления, пересекающегося с данным. Две дислокации, которые двигались вдоль пересекающихся направлений и столкнулись, взаимодействуют. В результате этого взаимодействия образуется новая дислокация. Она расположена так, что не может двигаться ни в одном из пересекающихся направлений скольжения и поэтому оказывается оседлой, покоящейся. О ней говорят: «сидячая дислокация». Каждая пара встретившихся дислокаций образует одну «сидячую». Все «сидячие» дислокации возникают близко друг от друга в области пересечения плоскостей скольжения. В конце концов они сливаются и образуют трещину.
Механизм «по Коттреллу» отчетливо наблюдается во многих кристаллических телах. В качестве примера его действия приведена фотография структуры кристалла NаС1, который всесторонне сжимали с целью залечить имеющуюся в нем пору. Объем поры действительно уменьшился, но вокруг нее образовались трещины «по Коттреллу».