МОДЕЛЬ: АНСАМБЛЬ ПУЗЫРЬКОВ

МОДЕЛЬ: АНСАМБЛЬ ПУЗЫРЬКОВ

Поговорим в начале главы об одной мудрой и красивой модели кристалла. По пути к концу книги она нам понадобится много раз.

О модели мертвого кристалла или, быть может, правильнее о мертвой модели кристалла мы недавно вспоминали: деревянные шарики — атомы, соединяющие их проволочки — символы связей, существующего взаимодействия. Здесь — о модели кристалла, в которой взаимодействие между атомами не заморожено. О ней, великолепно иллюстрирующей (другие причастия: передающей, отражающей) структуры реального кристалла и имеющиеся в нем дефекты, следует рассказать, а затем и воспользоваться ею. Модель эта не нова. Была она придумана выдающимся английским кристаллофизиком Л. Бреггом еще в начале 40-х годов нашего столетия, а затем осуществлена им и его сотрудниками Д. Наем и В. Ломером. Так мы ее и будем называть: модель БНЛ — Брегга — Ная — Ломера.

Пожалуй, самое важное следствие взаимодействия между атомами в кристалле непосредственно вытекает из простейшего факта, который состоит в том, что расстояние между двумя соседними атомами в кристалле при постоянной температуре имеет вполне определенную величину. Это — результат эксперимента, святая святых науки о кристалле. Речь, разумеется, идет о расстоянии между положениями, около которых атомы совершают колебания. Определенное расстояние — это означает, что, если мы попытаемся искусственно его увеличить, атомы, противясь этому, будут друг к другу притягиваться, а если попытаемся его уменьшить, атомы будут отталкиваться, стремясь восстановить определенное расстояние между собой. При некотором расстоянии (именно его мы и назвали определенным) между атомами силы притяжения и отталкивания оказываются равными по величине. На этом расстоянии и расположены атомы в решетке.

Итак, только из факта наличия определенного расстояния между атомами следует, что взаимодействие между ними носит черты и притяжения, и отталкивания. В основе этих двух противоборствующих тенденций во взаимодействии лежат силы электрического происхождения. В кристаллах различного типа они проявляют себя различно: по-одному в металлах, по-иному в диэлектриках и совсем по-иному в полупроводниковых кристаллах. Не стану, не договаривая, намекать на существо этих различий и тем более не стану рассказывать об этом подробно. Здесь нам достаточно знать, что взаимодействие между атомами в кристалле носит черты и притяжения, и отталкивания одновременно.

Хорошо бы придумать такой прием моделирования, который передавал бы конкуренцию сил притяжения и отталкивания, а это и значит — не омертвлял бы взаимодействие между атомами в кристалле. Именно это и сделали авторы модели БНЛ! В качестве строительных элементов модели они использовали не глиняные и не деревянные шарики, а маленькие, абсолютно одинаковые мыльные пузырьки, которые в один слой расположены на поверхности мыльной воды. Плавающий плот из пузырьков и есть модель кристалла. На площади 100 см² можно расположить плот из более десяти тысяч пузырьков диаметром 1 мм. Это вполне макроскопический двумерный «кристалл», им можно моделировать многое, происходящее в реальном кристалле.

Осуществить модель БНЛ просто. Для этого нужно совсем элементарное оборудование: тарелка, игла от медицинского шприца, волейбольная камера и зажим, которым можно было бы с различной силой сжимать резиновую трубку-отросток волейбольной камеры. Тарелку надо почти доверху заполнить мыльной водой и добавить в нее несколько капель глицерина, для того чтобы пузырьки, которые мы будем выдувать на поверхности мыльной воды, получились устойчивыми. Надуть волейбольную камеру, зажать ее отросток и вставить в него иглу от шприца. Разумеется, тупым концом. Если поместить иглу под поверхность воды и немного ослабить зажим, из иглы одна за другой начнут выходить строго одинаковые порции воздуха, которые будут превращаться в столь же одинаковые мыльные пузырьки. В этом очерке — рассказ о взаимодействии между пузырьками, моделирующими атомы. О взаимодействии между атомами, составляющими кристалл, — в следующем.

Мыльные пузырьки не безучастны друг к другу. Два разобщенных мыльных пузыря на поверхности воды друг к другу притягиваются, а соприкоснувшись — отталкиваются друг от друга.

Попытаемся понять происхождение силы притяжения. Бесспорно следующее утверждение: сила появляется вследствие того, что сближение пузырьков сопровождается уменьшением связанной с ними избыточной энергии.

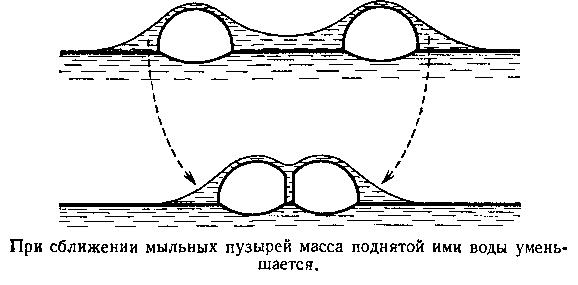
Поначалу хочется предположить, что эта энергия связана с поверхностью пузырей. Логика это желание легко подавит, подсказав, что поверхностная энергия не уменьшается при сближении пузырьков, а значит, их сближение окажется неоправданным. Есть, однако, иное слагаемое избыточной энергии совокупности двух пузырьков, которое оказывается зависящим от расстояния между ними. Дело в том, что каждый из пузырьков окружен областью, где уровень воды поднят над ее средним уровнем в сосуде. И следовательно, потенциальная энергия системы увеличена тем больше, чем большая масса воды и на бо?льшую высоту поднята. Степень поднятия убывает по мере удаления от центра пузырька. Если пузырьки удалены друг от друга на расстояние не очень большое, при котором области поднятия жидкости вокруг каждого из пузырьков частично перекрываются, их сближение оказывается выгодным, так как при этом уменьшается масса поднятой жидкости и, следовательно, связанная с ней избыточная потенциальная энергия. Приводимые рисунки качественно это поясняют.

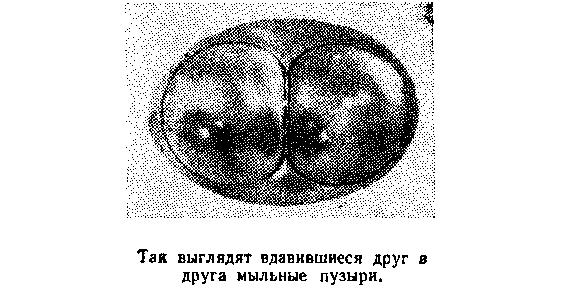
После того, как пузырьки соприкоснутся, прижимающая их сила увеличит давление заключенного в них газа и, следовательно, возникнет сила отталкивания. Обе силы — и притяжения, и отталкивания — нами найдены.

Итак, мы познакомились с моделью БНЛ: двумерный плот из огромного количества одинаковых мыльных пузырьков, взаимодействие между которыми не заморожено и отражает притяжение и отталкивание между атомами в реальных кристаллах.

В модели БНЛ нет пространственной периодичности реальных структур, двумерный плот может иметь только структуру плотной упаковки, подобную паркету, выложенному из шестигранных плит. Это — недостатки модели. Им противостоит огромное достоинство — в ней моделируется взаимодействие между элементами, составляющими кристалл.

Не будем упрекать модель в ее слабостях — и о которых упомянули, и о которых умолчали. Будем ей благодарны за ее сильные стороны.