ОПЫТЫ ПРОФЕССОРА ЛУКИРСКОГО

ОПЫТЫ ПРОФЕССОРА ЛУКИРСКОГО

Опыты эти были поставлены в условиях, не располагавших к академическим исследованиям. 1944 г., война, большая комната Казанского университета шкафами условно разделена на несколько маленьких, в каждой из них — группа физиков Ленинградского физико-технического института, эвакуированного в Казань. В одной из импровизированных комнаток — сотрудники профессора Петра Ивановича Лукирского. Много дел связано с работой на оборону (ими и занят профессор со своими сотрудниками), и как дань естественной любознательности ищущего ученого — опыты с монокристаллами каменной соли. Эти опыты стали классикой кристаллофизики, о них и рассказ.

И по замыслу, и по осуществлению опыты, о которых я буду рассказывать, очень подобны и отличаются лишь формой изучавшегося образца. В одном из опытов длительному высокотемпературному отжигу подвергался тщательно отполированный цилиндр монокристалла каменной соли. Ось цилиндра была ориентирована параллельно ребру куба естественной огранки кристалла.

Результат опыта: до отжига цилиндр бесшумно скатывался по слегка наклоненной поверхности стекла, а после отжига скатывание сопровождалось равномерным постукиванием, как если бы на поверхности цилиндра появились ребра — четыре ребра, равно отстоящих одно от другого. Эти ребра можно и увидеть, рассматривая отожженный цилиндр в отраженном свете.

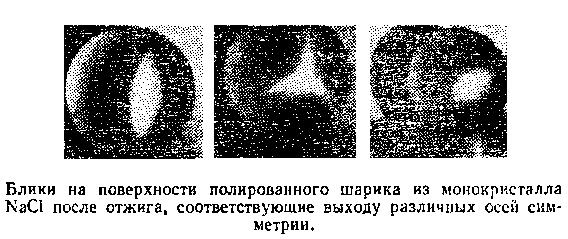
В другом опыте такому же отжигу подвергалась тщательно отполированная монокристальная сфера. Результат опыта: при рассматривании отжигавшейся сферы в отраженном свете на ее поверхности можно отчетливо увидеть фигурные блики, соответствующие выходу осей симметрии второго (эллиптический блик!), третьего (треугольный блик!) и четвертого (квадратный блик!) порядка. (Некоторая прямая в кристалле называется осью симметрии k-го порядка, если при повороте кристалла вокруг этой прямой на угол 360°/k он совмещается с самим собой.) До отжига сфера рассматривалась тщательно, этих бликов не было.

Общий результат обоих опытов можно сформулировать так: кристаллы соли, которым принудительно придана не свойственная им цилиндрическая или сферическая форма, стремятся к восстановлению формы куба — своей естественной огранки. Кристаллографы говорят «естественного габитуса». Высокая температура в этих опытах нужна лишь для того, чтобы придать активность какому-нибудь механизму переноса вещества кристалла, необходимому для формирования «естественного габитуса». Кристаллы, разумеется, предпочтут тот из механизмов, который обеспечит им возможность поскорее избавиться от принудительно заданной формы. Живой кристалл как бы не желает уступать черты первородства и борется за них.

Стремление к естественной огранке обусловлено тем, что среди несметного числа прочих мыслимых она обеспечивает наименьшую поверхностную энергию кристалла яри данном его объеме. Потому она и «естественная». К этой естественной огранке обязывает термодинамика, которая применительно к задаче об огранении кристалла выступает в форме правила Кюри — Вульфа. Первая фраза абзаца передает основную идею этого правила, мудрого и красивого своей простотой.

Правило Кюри — Вульфа может показаться противоречащим не менее мудрому утверждению геометрии, согласно которому из всех тел данного объема минимальную поверхность имеет сфера, и поэтому, если сферический монокристалл стремится к уменьшению поверхностной энергии, ему, казалось бы, не следует ограняться, так как при этом его поверхность лишь увеличится! Поверхность действительно увеличится — геометрия права! А вот энергия уменьшится, потому что при огранении исчезают участки поверхности, которые имеют большую удельную поверхностную энергию, и развиваются участки поверхности, представленные в «естественном габитусе», которые имеют малую поверхностную энергию. Проигрывается поверхность, но выигрывается энергия!

Опыты Лукирского качественно проиллюстрировали основную тенденцию, которой следуют кристаллы, самопроизвольно преобразуя собственную поверхность, и вызвали множество иных опытов, в которых этот процесс изучался точно, количественно. Ставились, например, такие опыты. Тщательно полировалась плоскость произвольного сечения кристалла. Его поверхность в равновесной огранке кристалла не представлена, и поэтому при высокой температуре зеркальная гладкость, заданная принудительно, должна будет нарушаться так, чтобы появились выгодные грани кристалла. В зависимости от ориентации плоскости произвольного сечения кристалла на ней будут появляться различные элементы так называемой «естественной шероховатости».

На стене нашей лаборатории много лет висят две фотографии поверхности зерна кристалла меди. Одну фотографию называют «лестница петергофского фонтана». На ней отчетливо видны чередующиеся светлые и темные полосы, которые в совокупности действительно напоминают лестницу, по которой сплошным потоком течет вода. Поверхность этого зерна меди была тщательно отполирована, а после отжига оно стало шероховатым, превратилось в совокупность ступеней, ребра которых направлены так же, как и ребра в ограненном монокристалле меди. А другая фотография поверхности зерна меди называется «палаточный городок». На ней видна совокупность остроконечных трехгранных выступов, которые ограничены теми же плоскостями, что и равновесный монокристалл.

Почему кристалл, рассеченный по произвольной плоскости, подобно сфере в опыте Лукирского, не ограняется в целом, а допускает формирование «петергофской лестницы» и «палаточного городка»? Да просто потому, что и «лестница», и «городок» лишь этапы на пути к истинному равновесию, этапы, которые завершаются быстрее, при меньшем переносе массы, чем достижение истинно равновесной формы всего кристалла. И на поверхности образцов Лукирского можно было наблюдать промежуточные формы. Однако благодаря тому, что при высокой температуре у кристаллов каменной соли быстро осуществляется нужный перенос массы, в опытах Лукирского процесс стремления к равновесной форме зашел настолько далеко, что можно было на сфере наблюдать блики и при качении цилиндра слышать постукивание.

Опыты Лукирского — впечатляющий пример самопроизвольного преобразования дефекта (поверхность!), которое, как обычно, сопровождается выделением энергии. Потому и самопроизвольного!

Проблема формы поверхности, ограничивающей кристалл (именно ей и посвящены опыты Лукирского), привлекала и привлекает к себе внимание многих крупнейших ученых — экспериментаторов и теоретиков. Ею занимались и американец К. Герринг, и наши отечественные выдающиеся физики-теоретики Я. И. Френкель, И. М. Лифшиц. Л. Д. Ландау этой проблеме посвятил специальную статью, которую с благодарственными словами в адрес А. Ф. Иоффе поместил в сборнике, приуроченном к его семидесятилетию.