ОТВЕТ НА ПРЯМО ЗАДАННЫЙ ВОПРОС
ОТВЕТ НА ПРЯМО ЗАДАННЫЙ ВОПРОС
Вопросу, который был задан естественным кристаллам каменной соли, предшествовала немалая работа физиков — и теоретиков, и экспериментаторов.
Вначале теоретики поставили и решили задачу, которая при первом знакомстве с ней кажется очень искусственной, экзотической, к вопросу отношения не имеющей. Задача вот какая. В кристалле на некотором расстоянии l друг от друга расположены две сферические полости. Для простоты пусть они будут одинаковыми и имеющими радиус R. Допустим, что изнутри к поверхностям полостей приложено всестороннее расширяющее давление Р. Предполагается, однако, что давление мало настолько, что создаваемые им напряжения не превосходят предела упругости кристалла. Это означает, что полости немного, лишь в меру упругой деформации кристалла, увеличивают свой радиус. Новый радиус полостей R1 окажется стабилизированным, а область кристалла, окружающая полость, окажется напряженной. В задаче спрашивается: не может ли под влиянием «внутреннего» давления Р как-то изменяться взаимное расположение полостей?
Решить такую задачу можно, следуя почти очевидной схеме. Надо найти величину упругой энергии, которая появилась в кристалле вследствие того, что к поверхностям полостей приложено давление. Эта энергия состоит из трех слагаемых: энергии поля напряжения вокруг одной полости, энергии поля напряжения вокруг другой полости (согласно условиям нашей задачи эти энергии должны быть между собой равны) и энергии, обусловленной тем, что полости расположены по соседству и связанные с ними напряжения как-то между собой взаимодействуют. Нетрудно также понять, что третье слагаемое, вообще говоря, должно зависеть от расстояния между полостями. А если третье слагаемое зависит от расстояния l, то от него зависит и энергия всей системы.
Вдумавшись в последнюю фразу, можно сразу же получить качественный ответ на вопрос, который сформулирован в задаче: две полости, распираемые изнутри всесторонним давлением, будут сближаться или удаляться в зависимости от того, как изменяется упругая энергия всего кристалла с изменением расстояния между полостями. Будет происходить то, что ведет к уменьшению энергии: если при уменьшении расстояния упругая энергия уменьшается, полости будут сближаться, если увеличивается — будут удаляться. Сформулированный качественный ответ безошибочен в той же мере, в какой безошибочна классическая механика.
Итак, на вопрос «не может ли?» ответ получен: «может!».
Следуя намеченной схеме, теоретики, проделав вычисления, получили нечто большее, чем качественный ответ, — он, как мы видели, появляется без всяких вычислений. Применительно к кристаллам каменной соли, которые имеют кубическую огранку, теоретики предсказали следующее: полости, расположенные параллельно ребру куба, будут слабо отталкиваться, а расположенные вдоль прямой, параллельной диагонали грани куба, будут сильно притягиваться.
Здесь оставим логику и предсказания теоретиков и познакомимся с деятельностью экспериментаторов. Они, ведомые теоретиками, действовали с открытыми глазами. Их эксперимент был прост: как и советовали теоретики, они следили за взаимодействием пар жидких включений в монокристалле каменной соли, расположенных либо вдоль ребра, либо вдоль диагонали грани куба. В эксперименте была одна хитринка, придуманная экспериментаторами. Именно благодаря ей эксперимент дал возможность четко задать кристаллу вопрос, о котором речь впереди. Дело в том, что, как нам известно, для взаимодействия включений необходимо создать внутреннее, распирающее их давление. Экспериментаторы его создали, слегка подогревая образец, разумно рассудив, что, так как коэффициент объемного расширения раствора соли в воде больше, чем собственно соли, в объеме нагретого включения должно возникать распирающее давление. Достаточно нагрева на 10 градусов, чтобы в объеме включения возникало распирающее давление, равное десяткам атмосфер.
Деятельность экспериментаторов завершилась успешно, во всяком случае они достоверно убедились в сближении тех пар, которые расположены вдоль диагонали грани куба, и наблюдаемый процесс засняли, воспользовавшись техникой покадровой киносъемки.
Здесь расстанемся с экспериментаторами, — свое дело они сделали не хуже теоретиков. Теперь все готово для того, чтобы обломку естественного кристалла, добытому в шахте, задать вопрос: был ли в истории его невообразимо долгой жизни нагрев? Не будем допытываться, когда он был, не будем интересоваться, каким он был, а был ли? Если был, то, очевидно, сближение включений, которое наблюдали экспериментаторы в условиях лабораторного опыта, должно было происходить и в естественных условиях. А если так, то близкие «диагональные» соседства жидких включений, естественно, должны отсутствовать, а «реберные» соседства должны быть в наличии. Именно об этом и свидетельствуют изучавшиеся образцы естественной каменной соли. Очень внимательно, воспользовавшись хорошим оптическим микроскопом, мы обследовали большое количество жидких включений в кристаллах каменной соли и убедились в том, что число близко расположенных пар включений тем больше, чем ближе их ориентация к «реберной». «Диагональных» соседств мы вообще не обнаружили.
На заданный вопрос кристалл ответил: нагрев был! В принципе можно получить ответы и на вопросы «когда» и «на сколько градусов», но лежат они под грудой громоздкой математики и ворохом экспериментальных кривых. Оставим профессионалам поиски ответов на эти вопросы.
В заключение этого очерка я хочу рассказать еще об одном опыте, который кое-что добавляет к ответу на прямо заданный вопрос.
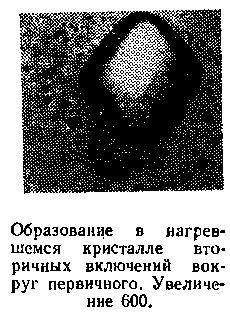
Давно, еще в 1954 г., очень красивый опыт по перегреву кристалла с включениями был выполнен Г. Г. Леммлейном. Он исследовал кристаллы натриевой селитры с замкнутыми жидкими включениями размером около 50 мкм. Кристаллы подвергались значительному перегреву, на величину около 100 °С. После перегрева вокруг первичных включений обнаруживался ореол мелких включений, которые располагались лишь в плоскостях легкого распространения трещин. Ясно, что произошло. Под влиянием внутреннего давления, возникшего при перегреве, вокруг включений возникли трещины, которые заполнились жидким раствором. А затем при охлаждении трещины, залечиваясь, распались на большое количество мелких включений, — подробно об этом рассказано в очерке «В кристалле была трещина». На фотографии, полученной Леммлейном, видно, что во включении, породившем ореол мелких, образовался газовый пузырек. Можно быть уверенным, в том, что его объем практически равен сумме объемов мелких вторичных включений, забравших часть жидкого раствора из первичного. Итак, если вокруг «первичного» макроскопического жидкого включения в ископаемом минерале обнаруживается ореол «вторичных», которые в основном расположены в одной плоскости, можно быть уверенным, что в истории кристалла был нагрев. Кристаллографы и геологи с такими минералами встречаются часто.