Глава 37 МАГНИТНЫЕ МАТЕРИАЛЫ
Глава 37
МАГНИТНЫЕ МАТЕРИАЛЫ
§ 1.Сущность ферромагнетизма
§ 2.Термодинамические свойства
§ 3. Петля гистерезиса
§ 4.Ферромагнитные материалы
§ 5.Необычные магнитные материалы
§ 1. Сущность ферромагнетизма
В этой главе мы поговорим об особенностях и поведении ферромагнетиков и некоторых других необычных магнитных материалов. Но перед тем как приступить к этой теме, я сделаю маленький обзор некоторых вопросов общей теории магнитов, которые мы изучали в предыдущей главе.
Мы сначала представили себе «магнитные» токи, текущие внутри материала и порождающие магнетизм, а затем стали их описывать через объемную плотность токов jмar=СXM. Заметьте, что эти токи нереальные. Даже когда намагниченность вещества однородна, токи в нем на самом деле не исчезают полностью: круговые токи электрона в одном атоме и круговые токи электрона в другом атоме, перекрываясь, не дают в сумме точно нуль. Даже внутри каждого отдельного атома распределение магнетизма не очень гладкое. В атоме железа, например, намагниченность распределена более или менее по сферической поверхности не слишком близко к ядру, но и не слишком далеко от него. Таким образом, магнетизм в веществе — вещь довольно сложная в своих деталях и весьма нерегулярная. Но сейчас мы должны об этих сложностях забыть и рассматривать явление, пользуясь более грубой усредненной моделью. Только тогда становится верным утверждение о равенстве нулю среднего тока при М=0 в ограниченной внутренней области, большой по сравнению с размерами атома. Таким образом, под магнитным моментом единицы объема (намагниченностью) и под jмаг и т. п. на нашем теперешнем уровне рассмотрения мы понимаем среднее по областям, большим по сравнению с пространством, занимаемым отдельным атомом.
В предыдущей главе мы обнаружили, что ферромагнитные материалы обладают следующим интересным свойством: при температурах выше некоторой их магнитные свойства проявляются слабо и лишь ниже этой температуры они становятся сильными магнетиками. Этот факт легко продемонстрировать. Кусок никелевого провода при комнатной температуре притягивается магнитом. Но если мы его нагреем в пламени газовой горелки выше температуры Кюри, то он станет практически немагнитным и не будет притягиваться к магниту, даже если мы поднесем его совсем близко. Если же оставить его остывать возле магнита, то в тот момент, когда его температура упадет ниже критической, он внезапно снова притянется к магниту!
В общей теории магнетизма, которой мы пользуемся, предполагается, что за намагниченность ответствен спин электрона. Спин электрона равен 1/2 и сопровождается магнитным моментом, равным одному магнетону Бора: (m=mb=qeh/2m. Спин электрона может быть направлен либо вверх, либо вниз. Поскольку заряд электрона отрицателен, то магнитный момент его направлен вниз, когда спин направлен вверх, и направлен вверх, когда спин направлен вниз. В соответствии с нашим обычным соглашением магнитный момент электрона (А — число отрицательное. Мы нашли, что потенциальная энергия магнитного диполя в заданном приложенном поле В равна—m·B. Энергия вращающегося электрона зависит также и от расположения соседних спинов. Если в железе момент соседнего атома направлен вверх, то момент следующего атома имеет сильную тенденцию тоже направиться вверх. Именно это делает железо, кобальт и никель такими сильными магнетиками — все моменты атомов в них стремятся быть параллельными. И вот первый вопрос, который мы должны обсудить, — почему так происходит?
Вскоре после развития квантовой механики было замечено, что существуют чрезвычайно мощные кажущиеся силы (однако не магнитные и не другие известные силы), которые стараются выстроить спины соседних электронов противоположно один другому. Эти силы тесно связаны с силами химической валентности. В квантовой механике есть так называемый принцип запрета, который говорит, что два электрона не могут занимать в точности одно и то же состояние, т. е. они не могут находиться в тех же самых условиях в смысле положения и ориентации спина. Если два электрона находятся в одном и том же месте, то единственной возможностью им различаться будет только противоположное направление их спинов. Таким образом, если между атомами имеется область пространства, где скапливаются электроны(так происходит при химической связи), и если на сидящий уже там электрон нам захочется посадить другой, то единственный способ это сделать — направить спин второго электрона противоположно спину первого. Параллельность спинов противоречит принципу запрета, если, конечно, электроны расположены в одной точке. В результате пара близких друг к другу электронов с параллельными спинами обладает гораздо большей энергией, нежели пара электронов с противоположными спинами; в целом же эффект будет таким, как будто действует сила, старающаяся развернуть спины противоположно друг другу. Иногда такие «спин-вращающие» силы называются обменными, но это название только увеличивает таинственность, так что термин этот не слишком удачен. Стремление электронов иметь противоположные спины обязано просто принципу запрета. Но фактически это объясняет отсутствие магнетизма почти у всех веществ! Спины свободных электронов на окраине атомов стремятся уравновешиваться в противоположных направлениях. Проблема заключается в том, чтобы объяснить, почему же материалы, подобные железу, ведут себя совсем не так, как ожидается.
Предполагаемый эффект выстраивания мы учитывали добавлением в выражение для энергии подходящего слагаемого, приговаривая, что если соседние электронные магнитики дают среднюю намагниченность М, то магнитный момент электрона имеет сильную тенденцию смотреть в том же самом направлении, что и средняя намагниченность соседних атомов. Таким образом, для двух возможных ориентации спинов можно написать:

Когда стало ясно, что квантовая механика может объяснить нам огромные спин-ориентирующие силы, пусть даже с очевидно неправильным знаком, то было предложено, что ферромагнетизм возникает именно за счет этих сил, но что вследствие сложности железа и большого числа участвующих в игре электронов знак энергии электронов получается обратным. Как только это стало ясно, т. е. примерно с 1927 г., когда была понята квантовая механика, многие исследователи стали делать разные оценки, прикидки, полуподсчеты, стремясь получить теоретически величину К. Но все равно наиболее поздние вычисления энергии взаимодействия между двумя электронными спинами в железе, предполагавшие прямое взаимодействие между двумя электронами в соседних атомах, дали неправильный знак. Сейчас, описывая это явление, говорят, что за все как-то ответственна сложность ситуации и что есть надежда, что кому-то, кто сумеет проделать вычисления для более сложного случая, удастся получить правильный ответ!
Полагают, что направленный вверх спин одного из электронов внутренней оболочки, который ответствен за магнетизм, стремится заставить спины электронов проводимости, витающих вокруг него, повернуться в противоположную сторону. Можно надеяться, что это ему вполне удастся, ибо электроны проводимости движутся в той же самой области, что и «магнитные» электроны. А поскольку они движутся то туда, то сюда, то могут передать свой приказ перевернуться «вверх ногами» спинам электронов других атомов; таким образом, «магнитный» электрон заставляет электрон проводимости направить спин в противоположную сторону, а тот в свою очередь заставляет следующий «магнитный» электрон направить свой спин противоположно его спину. Это двойное взаимодействие эквивалентно взаимодействию, стремящемуся выстроить два «магнитных» электрона в одном направлении. Иными словами, тенденция соседних спинов быть параллельными есть результат действия промежуточной среды, которая в некотором смысле стремится быть противоположной им обоим. Этот механизм не требует, чтобы все электроны проводимости были повернуты «вверх ногами». Достаточно, чтобы они лишь слегка стремились повернуться вниз, и шансы «магнитных» электронов повернуться вверх перевесят. Как полагают те исследователи, которые работали с этими вещами, это и есть тот механизм, который ответствен за ферромагнетизм. Но должен отметить, что вплоть до сегодняшнего дня никто не может вычислить величину l материала, зная просто, что в периодической системе элементов этот материал стоит, скажем, под номером 26. Короче говоря, мы все еще не можем понять явление до конца.
Теперь же продолжим рассуждения о нашей теории, а потом вернемся снова назад и обсудим некоторые ошибки избранного нами пути. Если магнитный момент какого-то электрона направлен вверх, то его энергия частично обусловлена внешним полем, а частично связана с тенденцией спинов быть параллельными. Поскольку при параллельных спинах энергия меньше, то эффект получается таким же, как и от «внешнего эффективного поля». Но помните, что обязано это не истинным магнитным силам, а более сложному взаимодействию. Во всяком случае, в качестве выражений для энергии двух спиновых состояний «магнитного» электрона мы примем уравнения (37.1). Относительная вероятность этих двух состояний при температуре Т пропорциональна exp[-энергия/kT], что можно записать как е±х, где х=|m|(H+lM/e0с2)/kT. Если затем мы вычислим среднюю величину магнитного момента, то найдем (как и в предыдущей главе), что она равна
M=N |m|thx. (37.2)
Теперь я могу подсчитать внутреннюю энергию материала. Отметим, что энергия электрона в точности пропорциональна магнитному моменту, так что все равно, вычислять ли средний момент или среднюю энергию. Среднее значение энергии будет при этом
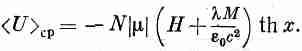
Но это не совсем верно. Выражение lM/e0c2 представляет взаимодействие всех возможных пар атомов, а мы должны помнить, что каждую пару следует учитывать только один раз. (Когда мы учитываем энергию одного электрона в поле остальных, а затем энергию второго электрона в поле остальных, то мы еще раз учитываем часть первой энергии.) Поэтому выражение взаимодействия мы должны разделить на 2 и наша формула для энергии приобретет вид
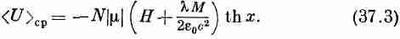
В предыдущей главе мы обнаружили одну очень интересную особенность: для каждого материала ниже определенной температуры существует такое решение уравнений, при котором магнитный момент не равен нулю даже в отсутствие внешнего намагничивающего поля. Если в уравнении (37.2) мы положим Н=0, то найдем
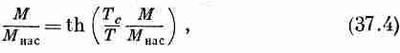
где Мнас=N|m| и Tc=|m|lMнас./ke0c2. Решив это уравнение (графически или каким-то другим способом), мы найдем, что отношение М/Мнаскак функция от T/Tcпредставляет кривую, названную на фиг. 37.1 «квантовая теория».
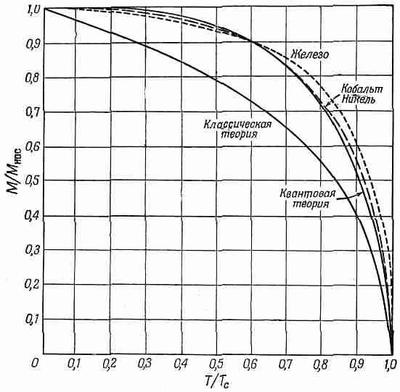
Фиг. 37.1. Зависимость спонтанной намагниченности (Н=0) ферромагнитных кристаллов от температуры.
Пунктирная кривая «Кобальт, Никель» — это полученная экспериментально кривая для кристаллов этих элементов. Теория и эксперимент находятся в разумном согласии. Там же представлены результаты классической теории, в которой вычисления проводились в предположении, что атомные магнитики могут иметь всевозможные ориентации в пространстве.
Можете убедиться, что это предположение приводит к предсказаниям, которые весьма далеки от экспериментальных данных.
Даже квантовая теория недостаточно хорошо описывает наблюдаемое поведение при высоких и низких температурах. Причина этого отклонения заключена в принятом нами довольно грубом приближении: мы предполагали, что энергия атома зависит лишь от средней намагниченности соседних с ним атомов. Другими словами, каждый атом со спином, направленным вверх, находящийся по соседству с данным атомом, из-за квантовомеханического эффекта выстраивания вносит свой вклад в энергию. А сколько таких атомов? В среднем это измеряется величиной намагниченности, но это только в среднем. Может оказаться, что для какого-то одного атома спины всех его соседей направлены вверх. Тогда его энергия будет выше средней. У другого же спины некоторых соседей направлены вверх, а некоторых — вниз, а среднее может быть нулем, и тогда никакого вклада в энергию вообще не будет и т. д. Из-за того что атомы в разных местах имеют различное окружение с различным числом направленных вверх и вниз спинов, нам следовало бы воспользоваться более сложным способом усреднения. Вместо того чтобы брать один атом, подверженный среднему влиянию, нам следовало бы взять каждый атом в его реальной обстановке, подсчитать его энергию, а затем найти среднюю энергию. Но как же все-таки определить, сколько соседей атомов направлено вверх, а сколько — вниз? Это как раз и нужно вычислить, но здесь мы сталкиваемся с очень сложной задачей внутренних корреляций,— задачей, которую никому еще не удавалось решить. Эта животрепещущая и интригующая проблема в течение многих лет волновала умы физиков; по этому вопросу писалось множество статей крупнейшими учеными, но и они не могли найти полного решения.
Оказывается, что при низких температурах, когда почти все атомные магниты направлены вверх и лишь некоторые направлены вниз, задача решается довольно легко; то же самое можно сказать и о высоких температурах, значительно превышающих температуру Кюри Тс, когда почти все они направлены совершенно случайно. Часто легко вычислить небольшие отклонения от некоторой простой идеализированной теории, и довольно ясно, почему такие отклонения имеются при низких температурах. Физически понятно, что по статистическим причинам намагниченность при высоких температурах должна исчезать. Но точное поведение вблизи точки Кюри никогда во всех подробностях не было установлено. Это очень интересная задача, над которой стоит потрудиться, если когда-нибудь вам вздумается взяться за еще не решенную проблему.
§ 2. Термодинамические свойства
В предыдущей главе мы заложили основу, необходимую для вычисления термодинамических свойств ферромагнитных материалов. Они, естественно, связаны с внутренней энергией кристалла, которая обусловлена взаимодействием между различными спинами и определяется формулой (37.3). Для нахождения энергии, связанной со спонтанной намагниченностью (ниже точки Кюри), мы можем в уравнении (37.3) положить Н=0 и, заметив, что thx=М/Мнас, найти, что средняя энергия пропорциональна М2:
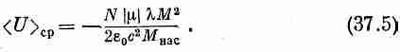
Если мы теперь построим график зависимости намагниченности от температуры, то получим кривую, которая описывается отрицательным квадратом функции (37.1) и представлена на фиг. 37.2, а. Если бы мы измеряли удельную теплоемкость такого материала, то получили бы кривую (фиг. 37.2, б), которая представляет производную кривой, изображенной на фиг. 37.2, а.
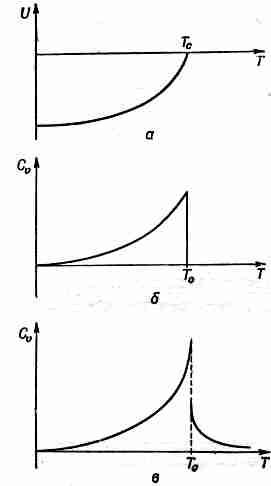
Фиг. 37.2. Энергия в единице объема и удельная теплоемкость ферромагнитного материала.
С увеличением температуры эта кривая медленно растет, но затем при Т = Тснеожиданно падает до нуля. Резкое падение вызвано изменением наклона кривой магнитной энергии, и кривая ее производной попадает прямо в точку Кюри. Таким образом, совершенно без магнитных измерений, лишь наблюдая за термодинамическими свойствами, мы бы смогли установить, что внутри железа или никеля что-то происходит. Однако как из эксперимента, так и из улучшенной теории (с учетом внутренних флуктуации) следует, что эти простые кривые неправильны и что истинная картина на самом деле более сложна. Пик этих кривых поднят выше, а падение до нуля происходит несколько медленнее. Даже если температура достаточно велика, так что спины в среднем распределены совершенно случайно, все равно попадаются области с определенным значением намагниченности, и спины в этих областях продолжают давать небольшую дополнительную энергию взаимодействия, которая медленно уменьшается с ростом температуры и увеличением беспорядка. Так что реальная кривая выглядит так, как показано на фиг. 37.2, в. Одна из целей физики сегодняшнего дня — найти точное теоретическое описание удельной теплоемкости вблизи точки перехода Кюри — захватывающая проблема, не решенная до сих пор. Естественно, что эта проблема очень тесно связана с формой кривой намагничивания в той же самой области.
Опишем теперь некоторые эксперименты, отнюдь не термодинамического характера, которые показывают, что мы все же в каком-то смысле правы в нашей интерпретации магнетизма. Когда материал при достаточно низких температурах намагничен до насыщения, то М очень близка к Мнас, т. е. почти все спины, равно как и магнитные моменты, параллельны. Это можно проверить экспериментально. Предположим, что мы подвесили магнитную палочку на тонкой струне, а затем окружили ее катушкой, так что можем менять магнитное поле, не притрагиваясь к магниту и не прикладывая к нему никакого момента сил. Это очень трудный эксперимент, ибо магнитные силы столь велики, что любая нерегулярность, любой перекос или несовершенство в железе могут дать случайный момент. Однако такой эксперимент был выполнен со всей необходимой аккуратностью и роль случайных моментов была сведена до минимума. С помощью магнитного поля катушки, которая окружает палочку, мы сразу можем перевернуть все магнитные моменты. Когда мы это проделаем, то заодно «сверху вниз» перевернутся и все моменты количества движения, связанные со спином (фиг. 37.3).
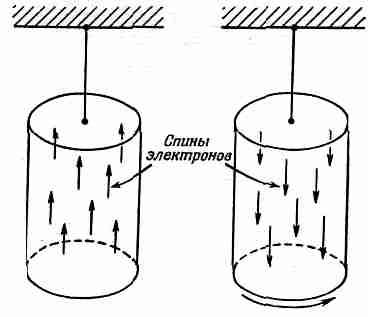
Фиг. 37.3. При перемагничивании железного бруска он приобретает некоторую угловую скорость.
Но поскольку момент количества движения должен сохраняться, то, когда все спины перевернулись, момент количества движения палочки должен измениться в противоположную сторону. Весь магнит должен начать вращаться. Это произошло на самом деле. Когда опыт был проделан, то было обнаружено слабое вращение магнита. Мы можем измерить полный момент количества движения, переданный всему магниту, который просто равен произведению N на h и на изменение момента количества движения каждого спина. Оказалось, что измеренное этим способом отношение момента количества движения к магнитному с 10%-ной точностью совпадает с нашими вычислениями. На самом деле в наших вычислениях мы исходили из того, что атомный магнетизм целиком обязан электронным спинам, однако в большинстве материалов есть еще и орбитальное движение. Орбитальное движение связано с решеткой, но она дает в магнетизм вклад не более нескольких процентов. Действительно, если взять Mнас=Nm и для плотности железа взять значение 7,9, а для m—момент электрона, связанный с его спином, то для магнитного поля получим насыщение около 20 000 гс. Однако опыт показывает, что на самом деле оно имеет значение вблизи 21500 гс. Ошибка в 5 или 10% возникает как раз из-за того, что мы пренебрегли вкладами орбитальных моментов. Таким образом, небольшое расхождение с гиромагнитными измерениями совершенно понятно.
§ 3. Петля гистерезиса
Из нашего теоретического анализа мы заключили, что магнитные материалы ниже некоторой температуры должны становиться спонтанно намагниченными, так что все магнитики в них должны смотреть в одном и том же направлении. Однако для обычного куска ненамагниченного железа это, как мы знаем, неверно. Почему железо не намагничивается все целиком? С помощью фиг. 37.4 я могу объяснить вам это. Допустим, что все железо было бы одним большим кристаллом такой формы, как показано на фиг. 37.4, а, и этот кристалл целиком намагнитился бы в одном направлении.
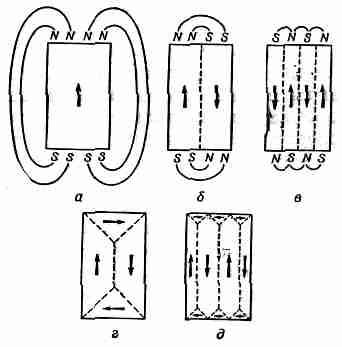
Фиг. 37.4. Образование доменов в монокристалле железа.
При этом создалось бы значительное внешнее магнитное поле, содержащее в себе огромную энергию. Мы можем уменьшить эту энергию поля, если расположим атомы так, чтобы одна часть кубика была намагничена вверх, а другая — вниз, как показано на фиг. 37.4, б. При этом, разумеется, поле вне железа будет занимать меньший объем и будет нести в себе меньше энергии.
Постойте, постойте! В слое между двумя областями рядом с электронами со спином, направленным вверх, сидят электроны со спином, направленным вниз. Но ферромагнетизм появляется только в тех материалах, для которых энергия уменьшается, когда спины параллельны, а не противоположны. Так что вдоль пунктирной линии на фиг. 37.4, б возникает некоторая добавочная энергия. Эта энергия иногда называется энергией стенки. Область, имеющая только одно направление намагниченности, называется доменом. На каждой единице площади разделяющей поверхности между двумя доменами у стенки домена, с противоположных сторон которой у нас расположены атомы, чьи магнитные моменты направлены противоположно, сосредоточена энергия. Конечно, нельзя говорить строго, что на границе моменты двух соседних атомов в точности противоположны, природа-то сделала этот переход более постепенным. Но сейчас нам не стоит интересоваться такими тонкими деталями.
Главный же вопрос теперь заключается вот в чем: выгодны такие стенки или нет? Ответ на него зависит от размеров доменов. Предположим, что мы увеличили размеры так, что все стало вдвое больше. При этом объем внешнего пространства, заполненного магнитным полем данной силы, станет в восемь раз больше, а энергия магнитного поля, которая пропорциональна объему, тоже возрастет в восемь раз. Но площадь границы между двумя доменами, на которой сосредоточена энергия стенки, возрастет только в четыре раза. Следовательно, если кусок железа достаточно велик, ему выгодно расщепиться на некое число доменов. Вот почему лишь очень маленькие кристаллы могут состоять только из одного домена. Любой большой объект, размер которого больше приблизительно одной тысячной миллиметра, будет иметь по крайней мере одну междоменную стенку, а обычный «сантиметровый» объект расщепляется, как это показано на рисунке, на множество доменов. Расщепление на домены будет происходить до тех пор, пока энергия, необходимая на установление еще одной дополнительной стенки, не сравняется с уменьшением энергии магнитного поля вне кристалла.
Природа же нашла еще один способ понижения энергии. Полю нет никакой необходимости выходить наружу, если, как это показано на фиг. 37.4, г, взять маленькие треугольные области с направленной в сторону намагниченностью. При таком расположении, как на фиг. 37.4, г, внешнее поле полностью отсутствует, а площадь доменных стенок лишь незначительно больше.
Но это приводит к новой проблеме. Оказывается, что если намагнитить отдельный кристалл железа, то он изменяет свою длину в направлении намагничивания; так что «идеальный» куб с намагниченностью «вверх» уже не будет безупречным кубом. Его «вертикальный» размер будет отличаться от «горизонтального».Этот эффект называется магнитострикцией. В результате таких геометрических изменений небольшой треугольный кусочек, показанный на фиг. 37.4, г, не сможет больше, так сказать, «умещаться» в отведенном ему пространстве: в одном направлении кристалл становится слишком длинным, а в другом — слишком коротким. Фактически-то он, конечно, умещается, но только немного сплющивается, что приводит к некоторым механическим напряжениям. Отсюда возникает и дополнительная энергия. Полный баланс вкладов в энергию и определяет сложный вид расположения доменов в куске ненамагниченного железа.
А что получится, если мы приложим внешнее магнитное поле? В качестве простого примера рассмотрим кристалл, домены которого показаны на фиг. 37.4, д. Если мы приложим магнитное поле, направленное вверх, то как будет происходить намагничивание кристалла? Прежде всего средняя доменная стенка может передвинуться в сторону (направо) и уменьшить энергию. Она перемещается таким образом, чтобы область направления «вверх» стала больше области направления «вниз», Элементарных магнитиков, направленных по полю, становится больше, а это приводит к понижению энергии. Таким образом, в куске железа в слабых магнитных полях с самого начала намагничивания доменная стенка начнет двигаться и «съедать» области, намагниченные противоположно полю. По мере того как поле продолжает увеличиваться, весь кристалл постепенно превращается в один большой домен, в котором внешнее поле помогает сохранять направление «вверх». В сильном магнитном поле кристаллы намагничиваются в одну сторону как раз потому, что их энергия в приложенном поле уменьшается. Внешнее магнитное поле кристаллов теперь уже не так существенно.
А что если геометрия кристалла не так проста? Что если какая-то ось кристалла и его спонтанная намагниченность направлены в одну сторону, а мы прилагаем поле, направленное в другую, скажем под углом 45°? Можно думать, что домены повернутся так, чтобы их намагниченность стала параллельной полю, а затем они, как и прежде, смогут слиться в один домен. Но сделать это для железа нелегко, ибо энергия, необходимая для намагничивания кристалла, зависит от направления намагничивающего поля относительно кристаллической оси. Намагнитить железо в направлении, параллельном кристаллической оси, относительно легко, но для того чтобы намагнитить его в каком-то другом направлении, скажем под углом 45° к направлению оси, энергии требуется больше. Следовательно, если в таком направлении приложить магнитное поле, то сначала происходит рост доменов, намагниченных в одном из избранных направлений, близких к направлению приложенного поля, пока в эту сторону не будет направлена намагниченность всех областей. Затем при гораздо больших полях общая намагниченность постепенно поворачивается к направлению поля, как это показано на фиг. 37.5.
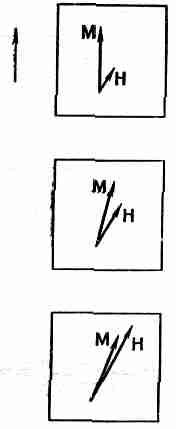
Фиг. 37.5. Намагничивающее поле Н, направленное под некоторым углом к кристаллической оси, постепенно изменяет направление намагниченности М, не изменяя ее величины.
На фиг. 37.6 показаны полученные из опыта кривые намагничивания монокристаллов железа.
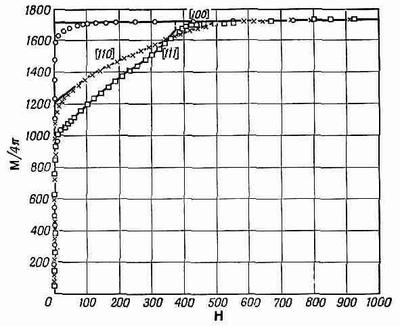
Фиг. 37.6. График компоненты М, параллельной полю Н, при различных направлениях Н (по отношению к осям кристалла).
Чтобы вы поняли их, я предварительно должен объяснить кое-какие обозначения, используемые для описания направлений в кристалле. Существует много способов расслоения кристалла на плоскости, в которых расположены атомы.
Каждый из вас, кто в прошлом работал или бывал в саду или на винограднике, знаком с этим любопытным зрелищем. Посмотрев в одну сторону, вы видите линию деревьев, а если посмотрите в другую,— вам откроется совсем другой ряд и т. д. Так и в кристалле — там есть определенные семейства плоскостей, содержащие много атомов; у таких плоскостей есть важная особенность (для простоты рассмотрим кубический кристалл). Если мы отметим, где эти плоскости пересекаются с тремя осями координат, то окажется, что обратные величины расстояний трех точек пересечения от начала относятся как целые числа. Эти три целых числа и принимаются для обозначения плоскостей. На фиг. 37.7, а, например, показана плоскость, параллельная плоскости yz. Она называется плоскостью (100), так как обратные величины отрезков, отсекаемых этой плоскостью по осям у и z, равны нулю.
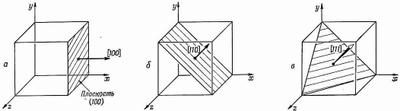
Фиг. 37.7. Способы обозначения кристаллических плоскостей.
Направление, перпендикулярное этой плоскости (в кубическом кристалле), задается тем же самым набором чисел, но записывается в квадратных скобках: [100]. Основную идею в случае кубического кристалла понять очень легко, ибо символ [100] обозначает вектор, который имеет единичную компоненту в направлении оси х и нулевые в направлениях осей у и. z. Комбинация [110] обозначает направление под 45° к осям x и y, как показано на фиг. 37.7, б, а [111] — направление диагонали куба (фиг. 37.7,в).
Вернемся теперь к фиг. 37.6. На ней мы видим кривые намагничивания монокристалла в различных направлениях. Прежде всего заметьте, что для очень слабых полей, столь слабых, что в нашем масштабе их трудно изобразить, намагниченность чрезвычайно быстро возрастает до весьма больших значений. Если приложить поле в направлении [100], т. е. в одном из направлений легкого намагничивания, то кривая идет вверх до еще большего значения, затем несколько закругляется и наступает насыщение. Происходит это потому, что домены, которые уже там есть, ликвидируются очень легко. Чтобы передвинуть доменные стенки и «проглотить» все «неправильные» домены, требуется совсем слабое поле. Монокристаллы железа обладают огромной проницаемостью (в магнитном смысле), гораздо большей, чем поликристаллическое железо. Совершенный кристалл намагничивается очень легко. Почему же его кривая все же закругляется? Почему она не идет прямо до насыщения? Точно не известно. Быть может, вам когда-нибудь удастся изучить это явление. Мы понимаем, почему при больших полях она плоская. Когда весь кубик становится единым доменом, то добавочное магнитное поле не может создать большей намагниченности, она уже равна Mнас— значит, спины всех электронов направлены вверх.
Что получится, если мы попытаемся повторить то же самое для направления [110], которое лежит в плоскости ху под углом 45° к оси х? Мы включаем небольшое поле, и намагниченность за счет роста домена резко увеличивается. Если затем мы продолжаем увеличивать поле, то выясняется, что для достижения насыщения поле должно быть довольно большим, ибо вектор намагниченности нужно повернуть в сторону от направления легкого намагничивания. Если это объяснение правильно, то при экстраполяции кривой [110] точка пересечения с вертикальной осью должна будет давать значение намагниченности, составляющее 1/Ц2от намагниченности насыщения. Оказывается, что так оно на самом деле и происходит. Это отношение очень-очень близко к 1/Ц2. Аналогично для направления [111], которое идет по диагонали куба, мы находим, как и ожидали, что при экстраполяции кривая пересекает вертикальную ось на расстоянии, составляющем 1/Ц2 от значения, соответствующего насыщению.
На фиг. 37.8 показано соответствующее поведение двух других ферромагнетиков: никеля и кобальта.
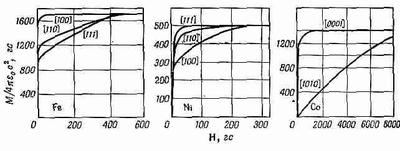
Фиг. 37.8. Кривые намагничивания для монокристаллов железа, никеля и кобальта.
Никель отличается от железа. Оказывается, что направлением легкого намагничивания у него будет направление [111]. Кобальт имеет гексагональную кристаллическую структуру; для этого случая система обозначений была изменена. Здесь в основании шестиугольника располагают три оси и еще одну ось, перпендикулярную к ним, так что здесь используется четыре числа. Направление [0001] — это направление гексагональной оси, а [1010]— направление, перпендикулярное к этой оси. Вы видите, что кристаллы различных металлов устроены по-разному.
Теперь мы рассмотрим такой поликристаллический материал, как обычный кусок железа. Внутри него содержится огромное множество маленьких кристалликов, кристаллические оси которых направлены во все стороны. Но это не то же самое, что домены. Вспомните, все домены были частью одного кристалла, а в куске железа, как видно из фиг. 37.9, содержится множество различных кристаллов с разной ориентацией.
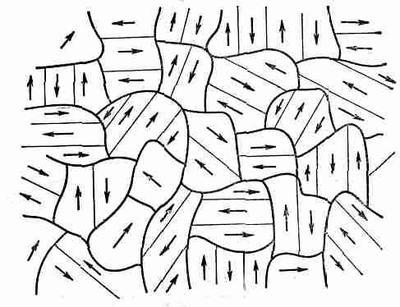
Фиг. 37.9. Микроструктура ненамагниченного поликристаллического ферромагнитного материала.
Каждый кристаллик имеет направление легкого намагничивания и разбивается на домены, которые обычно спонтанно намагничены в атом направлении.
В каждом из этих кристаллов, вообще говоря, содержится несколько доменов. Когда к куску поликристаллического материала мы прилагаем слабое магнитное поле, доменные барьеры в кристалликах начинают смещаться, и домены, направление намагниченности которых совпадает с направлением легкого намагничивания, растут все больше и больше. До тех пор пока поле остается очень малым, этот рост обратим; если мы выключим поле, намагниченность снова вернется к нулю. Этот участок кривой намагничивания обозначен на фиг. 37.10 буквой а.
Для больших полей в области, обозначенной буквой b, все становится гораздо более сложным. В каждом маленьком кристалле материала встречаются напряжения и дислокации, там есть примеси, грязь и дефекты. И при всех полях, за исключением лишь очень слабых, стенки доменов при своем движении наталкиваются на них. Между доменной стенкой и дислокацией (или границей зерна или примесью) возникают взаимодействия. В результате, когда стенка наталкивается на препятствие, она как бы приклеивается и держится там, пока поле не достигнет определенной величины. Затем, когда поле несколько подрастет, стенка внезапно срывается. Таким образом, движение доменной стенки оказывается отнюдь не плавным, как в идеальном кристалле: она движется скачкообразно, то и дело останавливаясь на мгновение. Если бы мы рассмотрели кривую намагничивания в микроскопическом масштабе, то увидели бы нечто подобное изображенному на вставке фиг. 37.10.
Но самое важное заключается в том, что эти прыжки намагничивания могут вызвать потерю энергии. Прежде всего, когда стенка домена проскакивает наконец через препятствие, она очень быстро движется к следующему. Быстрое движение влечет за собой и быстрое изменение магнитного поля, которое в свою очередь создает в кристалле вихревые токи. Последние растрачивают энергию на нагревание металла. Другой эффект состоит в том, что, когда домен неожиданно изменяется, часть кристаллов из-за магнитострикции изменяет свои размеры. Каждый неожиданный сдвиг доменной стенки создает небольшую звуковую волну, которая тоже уносит энергию. Благодаря таким эффектам эта часть кривой намагничивания необратима: происходит потеря энергии. В этом и заключается причина гистерезисного эффекта, ибо движение скачками вперед — одно, а движение назад — уже другое и в оба конца затрачивается энергия. Это похоже на езду по ухабистой дороге.
В конечном счете при достаточно сильных полях, когда все доменные стенки сдвинуты и намагниченность каждого кристаллика направлена по ближайшей к полю оси легкого намагничивания, остаются еще некоторые кристаллики, у которых ось легкого намагничивания далека от направления внешнего магнитного поля. Чтобы повернуть эти магнитные моменты, требуется еще дополнительное поле. Таким образом, в сильных полях именно в области, обозначенной на фиг. 37.10 буквой с, намагниченность возрастает медленно, но гладко.
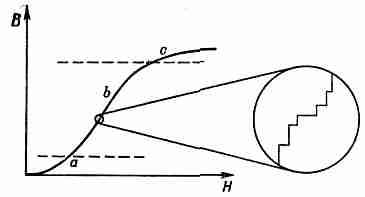
Фиг. 37.10. Кривая намагничивания поликристаллического железа.
Намагниченность не сразу достигает своего насыщения, ибо в этой последней части кривой происходит доворачивание атомных магнитиков в сильном поле. Таким образом, мы видим, почему кривая намагничивания поликристаллического материала обычно имеет вид, изображенный на фиг. 37.10: сначала она немного возрастает и это возрастание обратимо, затем возрастает быстро, но уже необратимо, а потом медленно загибается. Разумеется, между этими тремя областями никакого резкого перехода нет— они плавно переходят одна в другую.
Нетрудно убедиться в том, что процесс намагничивания в средней части кривой носит скачкообразный характер, что доменные стенки при сдвиге прыгают и даже щелкают. Для этого нам нужна только катушка со многими тысячами витков провода, связанная через усилитель с громкоговорителем (фиг. 37.11).
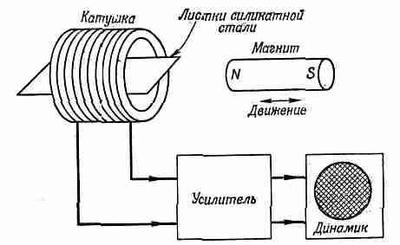
Фиг. 37.11. Скачкообразные изменения намагниченности листков кремнистой стали сопровождаются щелчками в громкоговорителе.
Если внутрь катушки поместить несколько листков кремнистой стали (такого же сорта, как и в трансформаторах) и медленно подносить к этой пачке постоянный магнит, то скачкообразные изменения намагниченности будут создавать в катушке импульсы э. д. с., которые в громкоговорителе будут слышны как отдельные щелчки. По мере приближения магнита к железу на вас обрушится целый град щелчков, напоминающий шум, создаваемый падающими друг на друга песчинками, высыпающимися из наклоненной жестянки. Это прыгают, покачиваются и щелкают доменные стенки по мере увеличения магнитного поля. Это явление называется эффектом Баркгаузена.
По мере приближения магнита к железным листикам шум некоторое время будет все возрастать, но когда магнит окажется совсем близко, шум начинает затихать. Почему? Да потому, что все доменные стенки передвинулись уже насколько возможно и теперь любое увеличение поля просто поворачивает векторы намагниченности в каждом из доменов, а это уже вполне плавный процесс.
Если вы теперь будете плавно отодвигать магнит так, чтобы вернуться назад по нижней петле гистерезиса, то все домены будут тоже стремиться вернуться назад в положение низшей энергии и вы снова услышите град щелчков. Обратите внимание, что если вы отодвинете магнит до какого-то определенного положения, а затем начнете немного двигать магнит взад и вперед, звук будет относительно слабым. Это снова напоминает поведение наклоненной жестянки с песком: когда песчинки «осели» на свое место, небольшой наклон жестянки уже не потревожит их. Небольшое изменение магнитного поля в железе неспособно заставить доменную стенку перескочить через «горб».
§ 4. Ферромагнитные материалы
Сейчас было бы хорошо рассказать о различных сортах магнитных материалов, применяемых в технике, и о некоторых проблемах, связанных с созданием магнитных материалов для разных целей. Прежде всего о самом термине «магнитные свойства железа», который часто приходится слышать. Он, строго говоря, не имеет смысла и способен ввести в заблуждение: «железо» как строго определенный материал не существует. Свойства железа существенно зависят от количества примесей, а также от способа его приготовления. Вы понимаете, что магнитные свойства будут зависеть от того, насколько легко движутся доменные стенки, именно это свойство будет определяющим, а совсем не то, как ведут себя отдельные атомы. Так что практически ферромагнетизм не является свойством атомов железа: это свойство куска железа в определенном состоянии. Железо, например, может находиться в двух различных кристаллических формах. Обычная форма имеет объемноцентрированную кубическую решетку, но может еще иметь и гранецентрированную решетку, которая, однако, стабильна только при температурах выше 1100°С. При этих температурах, разумеется, железо уже прошло точку Кюри. Однако, сплавляя с железом хром и никель (один из возможных составов содержит 18% хрома и 8% никеля), мы можем получить то, что называется нержавеющей сталью; хотя она и состоит главным образом из железа, но сохраняет гранецентрированную решетку даже при низких температурах. Благодаря своей кристаллической структуре этот материал обладает совершенно другими магнитными свойствами. Обычно нержавеющая сталь немагнитна в сколько-нибудь заметной степени, хотя есть сорта с другим составом сплава, которые в какой-то степени магнитны. Хотя такой сплав, как любое вещество, является магнетиком, он не ферромагнетик, как обычное железо, несмотря на то, что в основном он все же состоит из железа.
Существуют специальные материалы, которые были придуманы для получения особых магнитных свойств. О некоторых из них я хочу рассказать. Если нужно сделать постоянный магнит, то требуется найти материал с необычно широкой петлей гистерезиса, чтобы при выключении тока, когда мы спустимся к нулевому намагничивающему полю, намагниченность все же осталась большой. Для таких материалов границы доменов должны быть «заморожены» на месте как можно крепче. Одним из таких материалов является замечательный сплав АлникоV (51% Fe, 8% Аl, 14% Ni, 24% Со, 3% Cu). Довольно сложный состав этого сплава говорит о том кропотливом труде, который надо было затратить, чтоб создать хороший магнит. Сколько терпения потребовалось для того, чтобы, смешивая по-разному пять компонент, проверять разные составы их до тех пор, пока не был найден идеальный сплав! Когда АлникоV затвердевает, у него появляется «вторая фаза», которая, осаждаясь, образует множество маленьких зерен и вызывает очень большие внутренние напряжения. Движение доменных стенок в этом материале очень затруднено. А чтобы получить вдобавок нужное строение, Алнико V механически «обрабатывается» так, чтобы кристаллы выстраивались в форме продолговатых зерен в направлении будущей намагниченности. При этом намагниченность, естественно, стремится смотреть в нужном направлении и противостоять эффектам анизотропии. Более того, в процессе приготовления материал даже охлаждается во внешнем магнитном поле, так что зерна растут с правильной ориентацией кристаллов. Петля гистерезиса АлникоV приведена на фиг. 37.12.
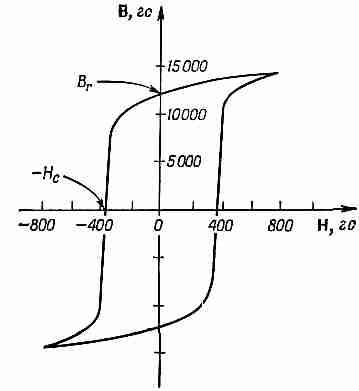
Фиг. 37.12. Петля гистерезиса сплава АлникоV.
Видите, она в 500 раз шире петли гистерезиса мягкого железа, которую я вам показывал (см.фиг.36.8, стр.146). Обратимся теперь к другим сортам материалов. Для изготовления трансформаторов и моторов необходим материал, который был бы «мягким» в магнитном отношении, т. е. такой, намагниченность которого могла бы легко изменяться, так что даже очень малое приложенное поле приводило бы к очень большой намагниченности. Для этого нужны чистые, хорошо отожженные материалы с очень малым количеством дислокаций и примесей, так чтобы доменные стенки могли легко двигаться. Анизотропию желательно сделать как можно меньше. Тогда если даже зерна материала расположены под «неправильным» углом по отношению к полю, материал все равно будет легко намагничиваться. Мы говорили, что железо предпочитает намагничиваться в направлении [100], тогда как никель предпочитает направление [111], так что если мы будем в различных пропорциях смешивать железо и никель, то можно надеяться найти такую их пропорцию, когда сплав не будет иметь никакого предпочтительного направления, т. е. направления [100] и [111] будут эквивалентны. Оказывается, что это достигается при смешивании 70% никеля и 30% железа. Вдобавок (вероятно, по счастливой случайности, а быть может, по какой-то физической взаимосвязи между анизотропией и магнитострикционными эффектами) оказалось, что константы магнитострикции железа и никеля имеют противоположные знаки. Для сплава этих двух металлов магнитострикция исчезает при содержании никеля около 80%. Так что при содержании никеля где-то между 70 и 80% у нас получаются очень «мягкие» магнитные материалы — сплавы, которые очень легко намагничиваются. Они называются пермаллоями. Пермаллои используются в высококачественных трансформаторах (при низких уровнях сигналов), но совершенно не годятся для постоянных магнитов. Приготовлять пермаллои и работать с ними нужно очень осторожно. Магнитные свойства пермаллоя в корне меняются, если его деформировать выше предела его упругости, так что этот материал никоим образом нельзя сгибать. Иначе в результате возникновения дислокаций, поверхностей скольжения и других механических деформаций проницаемость его уменьшается и границы доменов уже будут двигаться не так легко. Впрочем, былую высокую проницаемость можно восстановить отжигом при высокой температуре.
Полезно для характеристики различных магнитных материалов оперировать какими-то числами. Двумя такими характеристиками являются значения В и Н в точках пересечения петли гистерезиса с осями координат (фиг. 37.12). Эти значения называются остаточным магнитным полем Вrи коэрцитивной силой Нс. В табл. 37.1 приведены эти характеристики для некоторых материалов.

§ 5. Необычные магнитные материалы
Здесь мне бы хотелось рассказать о некоторых более экзотических магнитных материалах. В периодической таблице есть немало элементов, имеющих незаполненные внутренние электронные оболочки, а следовательно, и атомные магнитные моменты. Так, сразу вслед за ферромагнитными элементами — железом, никелем и кобальтом — вы найдете хром и марганец. Почему же они не ферромагнитны? Ответ заключается в том, что в выражении (37.1) член с К для этих элементов имеет противоположный знак. В решетке хрома, например, направления магнитных моментов атомов чередуются друг за другом (фиг. 37.13, б).
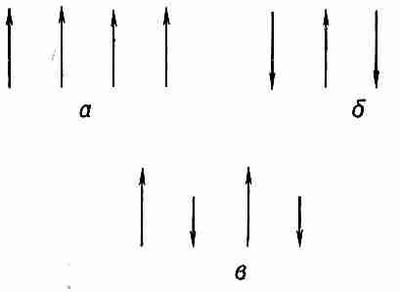
Фиг. 37.13. Относительная ориентация электронных спинов в различных материалах:
а — ферромагнетик;, б — антиферромагнетик; в — феррит.
Так что со своей точки зрения хром все же «магнетик», но с точки зрения технических применений это не представляет интереса, так как не дает внешнего магнитного эффекта. Таким образом, хром — пример материала, в котором кванто-вомеханический эффект вызывает чередование направлений спинов. Такой материал называется антиферромагнетиком. Упорядочивание магнитных моментов в антиферромагнитных материалах зависит и от температуры. Ниже критической температуры все спины выстраиваются в чередующейся последовательности, но если материал нагрет выше определенной температуры, которая по-прежнему называется температурой Кюри, направления спинов внезапно становятся случайными. Этот резкий внутренний переход можно наблюдать на кривой удельной теплоемкости. Он проявляется еще в некоторых особых «магнитных» эффектах. Например, существование чередующихся спинов можно проверить по рассеянию нейтронов на кристалле хрома. Нейтрон сам по себе имеет спин (и магнитный момент), поэтому амплитуда его рассеяния различна в зависимости от того, параллелен ли его спин спину рассеивателя или противоположен. В результате нейтронная интерференционная картина для чередующихся спинов отлична от картины при случайном их распределении.
Существует еще один сорт веществ, у которых квантово-механический эффект приводит к чередующимся спинам электронов, но которые тем не менее являются ферромагнетиками, т. е. их кристаллы имеют постоянную результирующую намагниченность. Идея, лежащая в основе объяснения свойств таких материалов, иллюстрируется схемой на фиг. 37.14.
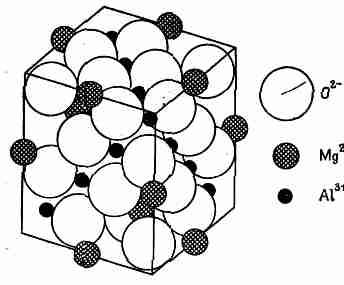
Фиг. 37.14. Кристаллическая структура минерала шпинель (MgOAl2O3).
Ионы Mg2+ занимают тетраэдрические места, и каждый из них окружен четырьмя ионами кислорода; ионы А13+ занимают октаэдрические места, и каждый окружен шестью ионами кислорода.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
1. Тонкая структура и магнитные аномалии
1. Тонкая структура и магнитные аномалии Мы изложили принципы волновой механики электрона. Теперь мы должны показать, почему, несмотря на ее успехи, эта механика в своей первоначальной форме оказалась все же несовершенной и должна претерпеть еще существенные изменения.
Магнитные жидкости
Магнитные жидкости Мы будем поступать здесь так же, как и раньше: начинать с очень простых фактов, а затем отыскивать их теоретическое объяснение. Рис. 321. Пусть у нас имеются два длинных магнита; один из них уравновешен так, что он занимает горизонтальное положение, а
1.4. Магнитные ppm
1.4. Магнитные ppm Первым известным магнитным ppm была машина Петра Пилигрима (1269 г.), уже описанная в начале этой главы (рис. 1.4).Новые виды магнитных вечных двигателей, появившиеся позже, основывались, так же как и первый, на аналогии между силой тяжести и силой притяжения
39. Свойства магнетиков и магнитные свойства тканей человека
39. Свойства магнетиков и магнитные свойства тканей человека Молекулы парамагнетиков имеют отличные от нуля магнитные моменты. При отсутствии магнитного поля эти моменты расположены хаотически и их намагниченность равна нулю. Степень упорядоченности магнитных
Магнитные поля в галактиках
Магнитные поля в галактиках В 1945 году известный уже нам английский астроном Ф. Хойл опубликовал свою гипотезу, согласно которой диффузная первоматерия Галактики сконцентрировалась под воздействием магнитного поля в два рукава, отходящие от центральной части,
97 Магнитные поля на бумаге
97 Магнитные поля на бумаге Для опыта нам потребуются: железные опилки (придется напилить из гвоздей), обычный маленький бытовой магнит, плотный лист бумаги, банка с подсолнечным маслом. Этот опыт потребовал от меня взять напильник и напилить из гвоздей, зажав их в тисках,
Глава 5
Глава 5 Когда дверь больницы открылась и выпустила конвой наружу, Тристам невольно зажмурился от яркого света. Вершины облачного семигорья, окружавшего город, сверкали такой чистой и ослепительной белизной, что ему пришлось идти за полицейскими с закрытыми глазами. Так,
Глава 6
Глава 6 Тюрьма, со слепыми, без единого окна, стенами, размещалась глубоко в недрах облака, на котором была построена Белая Столица. Оказавшись в камере, напуганные Тристам и Том какое-то время молча сидели на кровати, отведенной им на двоих, — в действительности это были
Глава 7
Глава 7 Прошло несколько часов. Тристам и Том лежали на жестких нарах в темной камере без окон, непрестанно ворочаясь с боку на бок. Лишь только напев флейты смолк, старик сразу задремал, что-то неразборчиво бормоча во сне.Тома снова начало знобить; Тристама же разбирал
Глава 8
Глава 8 С прохладным и сыроватым рассветным воздухом смешивался густой дым, валивший из печных труб. На всех перекрестках в центре Белой Столицы были расставлены люди снегобоя. Они походили не столько на стражей порядка, сколько на оккупационные войска.Тристам и Том в
Глава 9
Глава 9 Наступила ночь, за окнами стояла глубокая тишина. Тристам уснул. Рядом с ним, с раскрытой книгой на животе, спал, погруженный в грезы о будущем, Том.В глубине комнаты, растянувшись на матрасе, храпел один из полицейских. Второй сидел на лесенке, стоявшей теперь возле
Глава 10
Глава 10 Тристам внимательно следил за тенью. Она двигалась прямо на военный патруль.«Там ему не проскочить!» — забеспокоился Тристам.Но человек с рюкзаком, наверное, и сам это знал: он вскарабкался по стене и, словно черная кошка, перепрыгивая с крыши на крышу, за считанные
Глава 11
Глава 11 Наутро, как только мальчики проснулись, полицейские повели их вниз, в подземный ход. К счастью, в тесном тоннеле, по которому пришлось продвигаться гуськом, было чисто и сухо.— Долго еще? — спросил Тристам, когда они прошли метров десять.— Тс-с! — шепнул
Глава 13
Глава 13 Когда в гостиную вошел Том, Тристам сидел на диване. Он повесил мамин кулон себе на шею, заправив кристалл под свитер, и смотрел на портрет Миртиль, лежавший перед ним на низеньком столике. Глаза Тристама блестели, как будто он только что плакал.— Ну и тип! —
Магнитные, электрические и гравитационные поля
Магнитные, электрические и гравитационные поля Силовые линии магнитных полей играют большую роль во Вселенной и очень важны для понимания «Интерстеллар», поэтому стоит поговорить о них, прежде чем углубиться в научные аспекты фильма.Наверное, на уроках физики вам