Глава 6 ГАМИЛЬТОНОВА МАТРИЦА

Глава 6

ГАМИЛЬТОНОВА МАТРИЦА

§ 1. Амплитуды и векторы

§ 2. Разложение век­торов состояний

§ 3. Каковы базисные состояния мира?

§ 4. Как состояния меняются во времени

§ 5. Гамильтонова матрица

§ б. Молекула аммиака

Повторить: гл. 49) (вып. 4) «Собст­венные колеба­ния»

§ 1. Амплитуды и векторы

Прежде чем приступить к основной теме этой главы, мы хотели бы изложить несколько математических идей, которые часто встреча­ются в книгах по квантовой механике. Знание их облегчит вам чтение других книг или статей по этому предмету. Первая идея — это тесное математическое подобие между уравнениями квантовой механики и формулами для скаляр­ного произведения двух векторов. Вы помните, что если cи j — два состояния, то амплитуда начать в j и кончить в c может быть записана в виде суммы (по полной совокупности базис­ных состояний) амплитуд перехода из j в одно из базисных состояний и затем из этого базис­ного состояния уже в c:

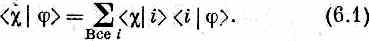
Мы объясняли это при помощи прибора Штер­на — Герлаха, но сейчас напоминаем вам, что в этих приборах нет нужды. Уравнение (6.1) — это математический закон, который верен всег­да, все равно, есть ли у нас фильтровальное оборудование или нет; вообще совсем не обя­зательно воображать наличие какого-то при­бора. Можно рассматривать это просто как формулу для амплитуды <c|j>.

Сопоставим (6.1) с формулой для скалярного произведения двух векторов В и А. Если В и А — обычные трехмерные векторы, то ска­лярное произведение можно написать так:

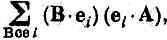
считая, что символ е_i обозначает любой из трех единичных векторов в направлениях х.у и z. Тогда B·e₁— это то, что обычно называют В_х, а В·е₂— то, что обычно называют B_y, и т,д. Значит, (6.2) эквивалентно

В_хА_х+В_уА_у+В_гА_г,

а это и есть скалярное произведение В·А.

Сравнение (6.1) с (6.2) обнаруживает следующую аналогию. Состояния c и j соответствуют двум векторам А и В. Базис­ные состояния i отвечают специальным векторам е_i, к которым мы относим все прочие векторы. Любой вектор может быть представлен как линейная комбинация трех «базисных векто­ров» е_i. Далее, если вам известны коэффициенты при каждом «базисном векторе» в этой комбинации, т. е. три его компонен­ты, то вы знаете о векторе все. Точно так же любое квантовомеханическое состояние может быть полностью описано ампли­тудами <i|j> перехода в базисные состояния, и если эти коэф­фициенты вам известны, то вы знаете все, что можно знать о состоянии. Из-за этой тесной аналогии то, что мы назвали «состоянием», часто именуют «вектором состояния».

Раз базисные векторы е_i перпендикулярны друг другу, то существует соотношение

Это соответствует соотношению (3.25) между базисными со­стояниями i

Теперь вы понимаете, почему говорят, что базисные состоя­ния i все «ортогональны друг другу».

Между (6.1) и скалярным произведением есть одно мини­мальное различие. У нас

а в векторной алгебре

А·В = В·А.

В квантовой механике с ее комплексными числами мы обязаны выдерживать порядок множителей, а в скалярном произве­дении порядок неважен.

Теперь рассмотрим такое векторное уравнение:

оно немножко необычно, но тем не менее верно. И означает оно то же самое, что и

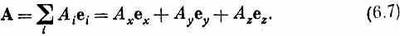
Заметьте, однако, что в (6.6) входит величина, отличная от скалярного произведения. Скалярное произведение — это про­сто число, а (6.6) — векторное уравнение. Одним из великих приемов векторного анализа было абстрагировать от уравне­ний идею самого вектора. Равным образом можно попытаться абстрагировать от уравнения (6.1) то, что в квантовой механике является аналогом «вектора». И это действительно можно сделать. Уберем <c| по обе стороны (6.1) и напишем такое урав­нение (не пугайтесь — это просто обозначение, и через пару минут вы узнаете, что означают эти символы):

Скобку <c|j> представляют себе состоящей из двух полови­нок. Вторую половинку |j> называют кет, а первую <c| на­зывают брэ (поставленные рядом они образуют брэ-кетєbгаcket, скоб-каєскобка — обозначение, предложенное Дираком); полусимволы <c| и |j> также называют векторами состоя­ний. Это не числа отнюдь, а нам вообще-то нужно, чтобы результаты наших расчетов выражались числами; стало быть, такие «незаконченные» величины представляют собой проме­жуточные шаги в расчетах.

До сих пор мы все свои результаты выражали с помощью чисел. Как же мы умудрялись избегать векторов? Забавно, что даже в обычной векторной алгебре можно сделать так, чтобы во все уравнения входили только числа. Например, вместо векторного уравнения типа

F=та всегда можно написать

C·F=C·(ma).

Получается уравнение, связывающее скалярные произведения и справедливое для любого вектора С. Но если оно верно для любого С, то едва ли имеет смысл вообще писать это С!

Теперь вернемся к (6.1). Это уравнение справедливо при любых c. Значит, для сокращения письма мы должны просто убрать c и написать вместо (6.1) уравнение (6.8). Это уравне­ние снабдит нас той же самой информацией, лишь бы мы пони­мали, что его всегда надлежит «завершить», «умножив слева на...», т. е. просто дописав некоторое <c| по обе стороны знака равенства. Следовательно, (6.8) означает в точности то же, что и (6.1),— ни более ни менее. Если вы предпочитаете числа, вы подставляете то <c|, которое вам нужно.

Может быть, вы в уравнении (6.8) уже нацелились и на j? Раз (6.8) справедливо при любом j, зачем же нам его держать? И действительно, Дирак предлагает абстрагироваться и от j, так что остается только

Вот он каков — великий закон квантовой механики! Этот закон утверждает, что если вы вставите любые два состояния c и j с обеих сторон, слева и справа, то опять вернетесь к (6.1). Уравнение (6.9) вообще-то не очень полезно, но зато является неплохим напоминанием о том, что уравнение выполняется для любых двух состояний.

§ 2. Разложение векторов состояний

Посмотрим на уравнение (6.8) еще раз; его можно рассмат­ривать следующим образом. Любой вектор состояния |j> может быть представлен в виде линейной комбинации совокуп­ности базисных «векторов» с подходящими коэффициентами, или, если угодно, в виде суперпозиции «единичных векторов» в подходящих пропорциях. Чтобы подчеркнуть, что коэффи­циенты <i|j> — это просто обычные (комплексные) числа, на­пишем

<i|j>=С_i. Тогда (6.8) совпадает с

Такое же уравнение можно написать и для всякого другого вектора состояния, скажем для |c>, но, конечно, с другими коэффициентами, скажем с D_i. Тогда будем иметь

где D_i — это просто амплитуды <i|c>.

Представим, что мы начали бы с того, что в (6.1) абстра­гировались бы от j. Тогда мы бы имели

Вспоминая, что <c|i>=<i|c>*, можно записать это в виде

А теперь интересно вот что: чтобы обратно получить <c|j>, можно просто перемножить (6.13) и (6.10). Только, делая это, надо быть внимательным к индексам суммирования, потому что они в разных уравнениях разные. Перепишем сперва (6.13):

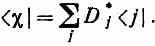
Это ничего не меняет. Объединяя с (6.10), получаем

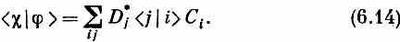
Вспомните, однако, что <j|i>=d_ij, так что в сумме останутся только члены с j=i. Выйдет

где, как вы помните, d*_i=<i|c>*=<c|i>, а C_i=<i|j>. Опять мы являемся свидетелями тесной аналогии со скалярным произведением

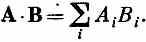
Единственная разница — что D_iнужно комплексно сопрягать. Значит, (6.15) утверждает, что если разложить векторы со­стояний <c| и |j> по базисным векторам <i| или |i), то ампли­туда перехода из j в c дается своего рода скалярным произве­дением (6.15). А это просто (6.1), записанное в других символах. Мы ходим по кругу, привыкая к новым символам.

Может быть, стоит подчеркнуть, что в то время, как про­странственные трехмерные векторы выражаются через три ортогональных единичных вектора, базисные векторы |i> квантовомеханических состояний должны пробегать всю совокуп­ность, отвечающую данной задаче. В зависимости от положения вещей в нее может входить два или три, пять или бесконечно много базисных состояний.

Мы говорили также о том, что происходит, когда частицы проходят через прибор. Если мы выпустим частицы в опре­деленном состоянии j, затем проведем их через прибор, а после проделаем измерение, чтобы посмотреть, находятся ли они в состоянии c, то результат будет описываться амплитудой

Такой символ не имеет близкого аналога в векторной алгебре. (Он ближе к тензорной алгебре, но эта аналогия не так уж полезна.) Мы видели в гл. 3 [формула (3.32)], что (6.16) можно переписать так:

Это пример двукратного применения основного правила (6.9).

Мы обнаружили также, что если вслед за прибором А по ставить другой прибор 5, то можно написать

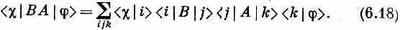
Это опять-таки следует прямо из предложенного Дираком метода записи уравнения (6,9). Вспомните, что между В и A всегда можно поставить черту (|), которая ведет себя совсем как множитель единица.

Кстати говоря, об уравнении (6.17) можно рассуждать и иначе. Предположим, что мы рассуждаем о частице, попадающей в прибор А в состоянии j и выходящей из него в состоянии y. Мы можем задать себе такой вопрос: можно ли найти такое состояние y, чтобы амплитуда перехода от yк c тождественно совпадала с амплитудой <c|A|j>?Ответ гласит да. Мы хотим, чтобы (6.17) заменилось уравнением

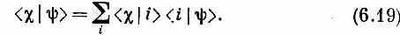
Конечно, этого можно достичь, если взять

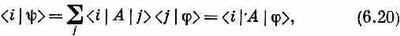
что и определяет собой y. «Но оно не определяет собой y,— скажете вы,— оно определяет только <i|y>». Однако <i|y> все же определяет y; ведь если у вас есть все коэффициенты, связывающие y с базисными состояниями i, то y опреде­ляется однозначно. И действительно, можно поупражняться с нашими обозначениями и записать (6.20) в виде

А раз это уравнение справедливо при всех г, то можно просто писать

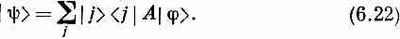
Теперь мы вправе сказать: «Состояние y — это то, что полу­чается, если начать с j и пройти сквозь аппарат A».

Еще один, последний пример полезных уловок. Начинаем опять с (6.17). Раз это уравнение соблюдается при любых c и j, то их обоих можно сократить! Получаем

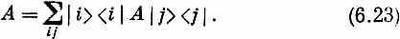
Что это значит? Только то, что получится, если вернуть на свои места j и c. В таком виде это уравнение «недокончено» и неполно. Если умножить его «справа» на |j>, то оно превра­щается в

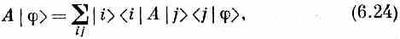
а это снова то же уравнение (6.22). В самом деле, мы бы могли просто убрать из (6.22) все j и написать

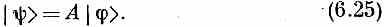
Символ А — это не амплитуда и не вектор; это вещь осо­бого рода, именуемая оператором. Он — нечто, что «опериру­ет» над состоянием, чтобы создать новое состояние; уравнение (6.25) говорит, что |y)> — это то, что получается, если А дей­ствует на |j>. Это уравнение тоже нужно считать недокончен­ным, открытым, пока слева оно не умножится на какое-то «брэ», скажем на <c|, и не обратится в

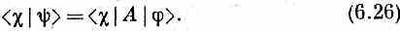
Оператор А, разумеется, полностью описывается тем, что за дается матрица амплитуд <i|A|j>;ее также пишут в виде А_ij— через любую совокупность базисных векторов.

Все эти математические обозначения на самом деле ничего нового не вносят. Единственный резон, почему мы их ввели,— мы хотели показать, как пишутся обрывки уравнений, потому что во многих книжках вы встретите уравнения, написанные в неполном виде, и нет причин вам пугаться, увидев их. Если вы захотите, вы всегда сможете дописать те части, которых не хватает, и получить уравнение, связывающее числа. Оно будет выглядеть более привычно.

Кроме того, как вы увидите, обозначения «брэ» и «кет» очень удобны. Прежде всего мы теперь сможем указывать со­стояния, задавая их вектор состояния. Когда мы захотим вести речь о состоянии с определенным импульсом р, то скажем: «состояние

|р>». Или будем говорить о некотором произволь­ном состоянии |y>. Для единообразия мы всегда, говоря о состоянии, будем употреблять «кет» и писать |y>. (Конечно, этот выбор совершенно произволен; в равной мере мы могли бы остановиться и на «брэ» <y|.)

§ 3. Каковы базисные состояния мира?

Мы обнаружили, что всякое состояние в мире может быть представлено в виде суперпозиции (линейной комбинации с подходящими коэффициентами) базисных состояний. Вы вправе спросить, во-первых: каких именно базисных состояний? Что ж, возможностей здесь немало. Можно, например, взять проек­цию спина на направление z или на некоторое другое направ­ление. Имеется очень-очень много различных представлений— аналогов различных систем координат, которые можно при­менять для представления обычных векторов. Затем можно спросить: с какими коэффициентами их брать? А это уж за­висит от физических обстоятельств. Различные совокупности коэффициентов отвечают разным физическим условиям. Здесь важно знать одну вещь — «пространство», в котором вы ра­ботаете, иными словами, знать, что эти базисные состояния означают физически. Так что первое, что вы, вообще говоря, должны знать,— это на что похожи базисные состояния. Тогда вам станет понятно, как описывать положение вещей на языке этих базисных состояний.

Мы хотели бы чуть-чуть заглянуть вперед и немножко по­говорить о том, каким скорей всего окажется общее квантовомеханическое описание природы — во всяком случае, каким оно будет, судя по нынешним физическим представлениям. Первым делом надо решиться на тот или другой выбор пред­ставления базисных состояний (всегда ведь возможны различ­ные представления). Например, для частицы со спином ¹/₂ можно использовать плюс- и минус-состояния относительно оси z. В оси z нет ничего особенного — можете выбрать любую ось, какую вам захочется. Но для единообразия мы всегда будем брать ось z. Начнем со случая одного электрона. Наряду с двумя возможностями для спина (вверх и вниз по оси z) электрон имеет еще импульс. Мы выбираем совокупность ба­зисных состояний, по одному на каждое значение импульса. А что если у электрона нет определенного импульса? Ничего страшного: мы ведь говорим только, каковы базисные состоя­ния. Если у электрона не будет определенного импульса, то у него какая-то амплитуда будет иметь один импульс, а какая-то — другой и т. д. А если он вертится не обязательно вверх спином, то у него есть какая-то амплитуда вертеться при этом импульсе спином вверх, а какая-то — вниз и т. д. Для пол­ного описания электрона, насколько нам сейчас известно, требуется только, чтобы базисные состояния описывались импульсом и спином. Значит, одна из приемлемых совокуп­ностей базисных состояний |i> для отдельного электрона ука­зывает различные значения импульса и еще направление, куда смотрит спин,— вверх или вниз. Различные смеси амплитуд, т. е. различные сочетания чисел С, описывают различные об­стоятельства. Что делает тот или иной электрон, описывается тем, что сообщается, с какой амплитудой у него спин может быть вверх, а с какой — вниз, и при этом импульс будет равен тому или иному числу, и так для всех мыслимых импульсов. Вы теперь видите, что требуется для полного квантовомеханического описания отдельного электрона.

А как обстоит дело с системами нескольких электронов? В этих случаях базисные состояния становятся сложнее. Пусть электронов пара. Во-первых, имеются четыре мыслимых состоя­ния по отношению к спину: у обоих электронов спины вверх, или у первого вверх, а у второго вниз, или у первого вниз, а у второго вверх, или у обоих вниз. Кроме того, нужно ука­зать, что у первого электрона импульс p₁ а у второго импульс р₂. Базисные состояния для двух электронов требуют указания двух импульсов и двух значков для спина. Для семерки элект­ронов нужно указать семь пар таких чисел.

Если же имеются протон и электрон, то нужно указать на­правление спина протона и его импульс и направление спина электрона и его импульс. По крайней мере, в каком-то при­ближении это так. Мы на самом деле не знаем, каким является правильное представление для нашего мира. Мы начинаем с предположения, что если указать спин и импульс электрона и то же самое для протона, то получатся базисные состояния; все это очень хорошо, но как быть с «протоньими внутренно­стями»? В самом деле, рассудим следующим образом. В атоме водорода, в котором имеются один протон и один электрон, приходится описывать множество различных базисных состояний, отмечать направления вверх и вниз у спинов про­тона и электрона и всевозможные импульсы протона и электро­на. Затем имеются различные комбинации амплитуд С_i;все вместе они описывают характер атома водорода в тех или иных состояниях. Но представьте, что мы смотрим на целый атом водорода, как на «частицу». Если бы мы не знали, что он со­стоит из протона и электрона, то могли бы сказать: «О, я знаю, какие у него базисные состояния — они соответствуют разным импульсам атома водорода». Но это на самом деле не так, ведь у атома водорода есть какие-то внутренние части. Значит, у него могут быть различные состояния с разной внутренней энергией, и описание реальной природы потребовало бы даль­нейших подробностей.

То же и с протоном. Вопрос стоит так: есть ли у протона внутренние части? Должны ли мы описывать протон, задавая все мыслимые состояния протонов, мезонов или странных ча­стиц? Мы этого не знаем. И даже хотя мы допускаем, что элект­рон прост и все, что можно о нем сказать,— это задать его импульс и спин, но ведь не исключена возможность завтра открыть наличие внутри электрона каких-то колесиков и ше­стеренок. А это будет означать, что наше представление не­полно, или неверно, или неточно, так же как и представление атома водорода, описывающее только его импульс, было бы неполным, потому что оно пренебрегало бы тем фактом, что атом водорода может оказаться возбужденным изнутри. Если электрон тоже может оказаться возбужденным изнутри и превратиться еще во что-то, например в мюон, то его следовало бы описывать не простым заданием состояний новой частицы, а, вероятно, в терминах более сложных внутренних колесиков. Главная сегодняшняя проблема в изучении фундаментальных частиц и состоит в том, чтобы открыть, каковы правильные представления для описания природы. В настоящее время мы полагаем, что для электрона достаточно указывать его импульс и спин. Но мы полагаем также, что существует идеализирован­ный протон, имеющий при себе свои p-мезоны, свои K-мезоны и т. д., и все они должны быть отмечены. Но ведь отмечать несколько десятков частиц смысла мало! Вопрос о том, что есть фундаментальная частица, а что — не фундаментальная,— вопрос, о котором столько сейчас говорится,— это вопрос о том, на что будет похоже окончательное представление в окон­чательном квантовомеханическом описании мира. Будет ли такая вещь, как импульс электрона, все еще способна описы­вать природу? И вообще нужно ли весь вопрос ставить именно таким образом! Такие мысли беспрерывно возникают в любом научном исследовании. Во всяком случае, проблема нам по­нятна — как найти представление? Но ответа мы не знаем. Мы даже не знаем, «в этом ли состоит» проблема или нет; но если проблема в этом, то сперва нужно попытаться узнать, «фунда­ментальна» или нет каждая отдельная частица.

В нерелятивистской квантовой механике, где энергии не очень высоки и где вы не затрагиваете внутреннего устройства странных частиц и т. п., вы можете делать весьма сложные расчеты, не заботясь об этих деталях. Вы можете просто оста­новиться на импульсах и спинах электронов и ядер и все будет в порядке. В большинстве химических реакций и других низко­энергетических событий в ядрах ничего не происходит; они не возбуждаются. Дальше, если атом водорода движется мед­ленно и если он спокойно стукается о другие атомы водорода и ничего внутри него не возбуждается, не излучается, никаких сложностей не происходит, а все остается в основном состоя­нии энергии внутреннего движения, — в этом случае вы мо­жете пользоваться приближением, при котором об атоме во­дорода говорят как об отдельном предмете, или частице, не за­ботясь о том, что он может что-то внутри себя с собой сделать. Это будет хорошим приближением до тех пор, пока кинетиче­ская энергия в любом столкновении будет заметно меньше 10 эв, т. е. энергии, требуемой для того, чтобы возбудить атом водо­рода до следующего внутреннего состояния. Мы часто будем прибегать к приближению, при котором исключается возмож­ность внутреннего движения, тем самым уменьшая число де­талей, которые должны быть учтены в наших базисных состояниях. Конечно, при этом мы опускаем кое-какие явления, которые проявляются (как правило) при каких-то высших энер­гиях, но такое приближение сильно упрощает анализ физиче­ских задач. Например, можно рассуждать о столкновении двух атомов водорода при низкой энергии (или о любом химическом процессе), не заботясь о том, что атомные ядра могут возбуж­даться. Итак, подведем итог. Когда мы вправе пренебречь влиянием любых внутренних возбужденных состояний части­цы, мы вправе выбрать базисную совокупность из состояний с определенным импульсом и z-компонентой момента количе­ства движения.

Первой проблемой при описании природы является отыска­ние подходящего представления для базисных состояний. Но это только начало. Надо еще уметь сказать, что «случится». Если известны «условия» в мире в один момент, то мы хотим знать условия в более поздний момент. Значит, надо также найти законы, определяющие, как все меняется со временем. Мы теперь обращаемся ко второй части основ квантовой меха­ники — к тому, как состояния меняются во времени.

§ 4. Как состояния меняются во времени

Мы уже говорили о том, как отображать ход событий, где мы что-то пропускаем через прибор. Но самый привлекатель­ный, самый удобный для рассмотрения «опыт» состоит в том, что вы останавливаетесь и ждете несколько минут, т. е. вы приготовляете состояние j и, прежде чем проанализировать его, оставляете его в покое. Быть может, вы оставите его в покое в каком-то электрическом или магнитном поле — все зависит от физических обстоятельств. Во всяком случае, ка­кими бы ни были условия, вы от момента t₁до момента t₂ ос­тавляете объект на свободе. Допустим, что он выпущен из на­шего первого прибора в состоянии j в момент t₁. А затем он проходит через «прибор», в котором он находится до момента t₂. Во время такой «задержки» могут продолжаться различные события, прилагаться внешние силы,— словом, что-то в это время случается. После такой задержки амплитуда того, что этот объект обнаружится в состоянии c, уже не та же самая, какой она была бы, если бы задержки не было. Так как «ожи­дание» — это просто частный случай «прибора», то можно опи­сать то, что происходит, задав амплитуду в том же виде, как в уравнении (6.17). Поскольку операция «ожидания» представляет особую важность, мы вместо А обозначим ее U, а чтобы отмечать начальный и конечный моменты t₁ и t₂, будем писать U (t₂, t₁). Интересующая нас амплитуда — это

Как и всякая подобная амплитуда, она может быть представ­лена в той или иной базисной системе в виде

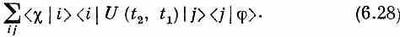
Тогда U описывается заданием полной совокупности амплитуд — матрицы

Кстати, следует отметить, что матрица <i|U(t₂, t₁|j> могла бы дать гораздо больше всяких деталей, чем нам обычно нужно. Теоретик высокого класса, работающий в физике высоких энергий, рассматривает примерно такие проблемы (потому что именно так обычно ставятся эксперименты): он начинает с двух частиц, скажем с протона и протона, налетающих друг на друга из бесконечности. (В лаборатории обычно одна частица покоится, другая же вылетает из ускорителя, кото­рый по атомным масштабам пребывает в бесконечности.) Они сталкиваются, и в итоге появляются, скажем, два К -мезона, шесть p-мезонов и два нейтрона с определенными импульсами в определенных направлениях. Какова амплитуда того, что это случится? Математика здесь выглядит так. Состояние j отмечает спины и импульсы сближающихся частиц. а c — это сведения о том, что получается в конце. К примеру, с какой амп­литудой вы получите шесть мезонов, идущих в таких-то и та­ких-то направлениях, а два нейтрона, вылетающих вот в этих направлениях и со спинами, торчащими так-то и так-то. Ины­ми словами, c отмечается заданием всех импульсов, спинов и т. п. конечных продуктов. И вот работа теоретика состоит в том, чтобы подсчитать амплитуду (6.27). Однако на самом деле его интересует только частный случай, когда t₁=-Ґ, а t₂ =+Ґ. (У нас не бывает экспериментальных данных о де­тальном ходе процесса, известно только, что вошло и что вышло. Предельный случай U (t₂, t₁)при t₁®-Ґ и t₂®+Ґ обозначается буквой S; теоретик нуждается в величине

<c|S|j>.

Или, если пользоваться формой (6.28), ему нужно вычислить матрицу

<i|S|j>,

называемую S-матрицей. Стало быть, если вы увидите физика-теоретика, который меряет шагами комнату и говорит: «Мне нужно только вычислить S-матрицу», — то вы теперь уже будете понимать, над чем он ломает голову.

Как анализировать S-матрицу, т. е. как указать законы для нее,— вопрос интересный. В релятивистской квантовой механике при высоких энергиях это делается одним способом, в нерелятивистской же квантовой механике — другим, более удобным. (Он годится и в релятивистском случае, но перестает быть таким удобным.) Состоит он в том, чтобы вывести U-мат­рицу для небольших интервалов времени, т. е. для близких t₂ и t₁. Если мы сможем найти последовательность таких U для последовательных интервалов времени, то сможем проследить за тем, как все меняется в зависимости от времени. Сразу же ясно, что для теории относительности этот способ не очень хорош, потому что не так уж просто указать, как «одновремен­но» все всюду выглядит. Но не стоит нам думать об этом; нашей заботой будет только нерелятивистская механика.

Рассмотрим матрицу U для задержки от t₁до t₃, где t₃ больше t₂. Иными словами, возьмем три последовательных момента: t₁ меньше t₂, t₂ меньше t₃. Тогда мы утверждаем, что матрица, которая тянется от t₁до t₃, получается перемноже­нием подряд всего того, что происходит при задержке от t₁ до t₂, и затем от t₂до t₃. Это в точности то же самое, что было с двумя последовательными приборами В и А. Тогда, следуя обозначениям, принятым в гл. 3, § 6, мы можем написать

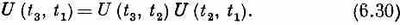
Иначе говоря, можно проанализировать любой интервал вре­мени, если мы умеем анализировать последовательность про­межуточных коротких интервалов. Мы просто перемножаем все куски; это и есть способ нерелятивистского анализа кван­товой механики.

Итак, задача состоит в том, чтобы узнать матрицу U(t₂, t₁) для бесконечно малого интервала времени — для t₂=t₁+Dt. Спросим себя: если сейчас у нас есть состояние j, то как оно будет выглядеть через бесконечно малое время Dt? Посмотрим, как это можно расписать. Обозначим состояние в момент t через |y(t)> (мы указываем зависимость y от времени, чтобы было совершенно ясно, что речь идет об условиях в момент t). Теперь зададим вопрос: каково будет положение вещей через короткое время Dt? Ответ таков:

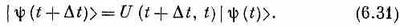
Здесь имеется в виду то же, что и в (6.25), а именно, что амплитуда обнаружить c в момент t+Dt есть

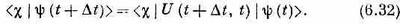
Поскольку мы еще не очень хорошо разбираемся в этих абстрактных вещах, то давайте спроецируем наши амплитуды в определенное представление. Умножая обе части (6.31) на <i|, получаем

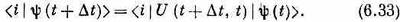
Можно также разложить и |y(t)> на базисные состояния и написать

Понять это можно так. Если через C_i(t)=<i|y|(t)> обозна­чить амплитуду пребывания в базисном состоянии i в момент t, то можно считать эту амплитуду (помните, это просто число!) меняющейся во времени. Каждое С_iстановится функцией времени t. Кроме того, у нас есть информация о том, как амп­литуды С_iменяются во времени. Каждая амплитуда в момент (t+Dt) пропорциональна всем прочим амплитудам в момент t, умноженным на ряд коэффициентов. Обозначим U-матрицу через U_ij, считая, что

U_ij=<i|U|j>.

Тогда (6.34) можно записать так:

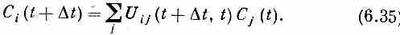
Вот как будет выглядеть динамика квантовой механики.

Нам пока мало известно об U_ij. Мы знаем только, что при Dt, стремящемся к нулю, ничего не должно произойти, просто должно получиться начальное состояние. Значит, U_ij®1 и U_ij®0 при i№j. Иными словами, U_ij®d_ij при Dt®0. Кроме того, мы вполне вправе предположить, что при малых At каж­дый из U_ijобязан отличаться от d_ij на величину, пропорцио­нальную Dt; так что можно писать

Однако обычно по историческим и по иным причинам из коэф­фициентов К_ijвыносят множитель

(-i/h) ; предпочитают писать

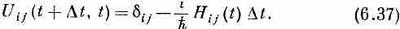
Это, разумеется, то же самое, что и (6.36). Если угодно, это просто определение коэффициентов H_ij(t).Члены H_ij— это как раз производные по t₂от коэффициентов U_ij(t₂, t₁), вычисляемые при t₂=t₁=t,

Подставляя в (6.35) этот вид U, получаем

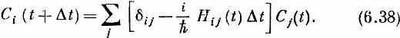
Суммируя члены с d_ij, получаем просто C_i(t), что можно пере­нести в другую сторону уравнения. После деления на Dt мы распознаем в этом производную

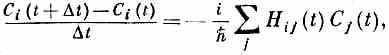
или

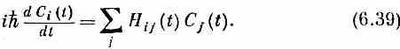
Вы помните, что С_i(t) — это амплитуда <i|y> обнаружить состояние y в одном из базисных состояний i (в момент t). Значит, уравнение (6.39) сообщает нам, как каждый из коэф­фициентов <i|y> меняется со временем. Но это все равно, что сказать, что (6.39) сообщает нам, как со временем меня­ется состояние y, раз мы описываем y через амплитуды < i|y>. Изменение y со временем описывается через матрицу Н_ij, которая, конечно, должна включать все то, что мы делали с системой, чтобы вызвать ее изменения. Если мы знаем матрицу H_{ij, которая содержит в себе всю физику явления и может, вообще говоря, зависеть от времени, то у нас есть полное опи­сание поведения системы во времени. Таким образом, (6.39)— это квантовомеханический закон для динамики мира.}

(Нужно сказать, что мы всегда будем выбирать совокуп­ность базисных состояний, которые фиксированы и со временем не меняются. Иногда используют такие базисные состояния, которые сами меняются. Однако это все равно, что пользова­ться в механике вращающейся системой координат, а мы не хотим входить в подобные тонкости.)

§ 5. Гамилътонова матрица

Идея, стало быть, заключается в том, что для квантовомеханического описания мира нужно выбрать совокупность базисных состояний i и написать физические законы, задавая матрицу коэффициентов Н_ij. Тогда у нас будет все, что нужно,— мы сможем отвечать на любой вопрос о том, что случится. Нам остается выучить правила, по которым находят Н в соответ­ствии с данной физической обстановкой: какое Н отвечает маг­нитному полю, какое электрическому и т. д. Это самая труд­ная часть дела. К примеру, для новых странных частиц мы со­вершенно не представляем, какие Н_ijупотреблять. Иными словами, никто не знает полного H_ijдля всего мира. (Частично трудность заключается в том, что едва ли можно надеяться на открытие Н_ij, раз никому не известно, каковы базисные со­стояния!) Мы действительно владеем превосходными прибли­жениями для нерелятивистских явлений и некоторых других особых случаев. В частности, мы знаем вид Н_ij, требуемый для движений электронов в атомах — для описания химии. Но мы не знаем полного, истинного Н для всей Вселенной.

Коэффициенты H_ijназывают гамильтоновой матрицей, или, короче, просто гамильтонианом. (Как получилось, что Гамильтон, работавший в 30-х годах прошлого века, дал свое имя квантовомеханической матрице,— история длинная.) Много лучше было бы называть ее энергетической матрицей по при чинам, которые станут ясны, когда мы поработаем с ней. Итак все сошлось на гамильтониане. Как узнать гамильтониан — вот в чем вопрос!

У гамильтониана есть одно свойство, которое выводится сразу же:

Н*_ij=H_ji. (6.40)

Это следует из того, что полная вероятность пребывания си­стемы хоть в каком-то состоянии не должна меняться. Если вначале у вас была частица (или любой объект, или весь мир), то с течением, времени она пропасть не может. Полная вероят­ность ее где-то найти равна

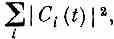
что не должно меняться со временем. Если это обязано выпол­няться для любого начального условия j, то уравнение (6.40) тоже должно соблюдаться.

В качестве первого примера возьмем случай, когда физические условия не меняются со временем; мы имеем в виду внешние физические условия, так что Н не зависит от времени никаких магнитов никто не включает и не выключает. Выберем также систему, для описания которой хватает одного базисного состояния; такое приближение годится для покоящегося атома водорода и сходных систем. Уравнение (6.39) тогда утверж­дает, что

Только одно уравнение — и все! Если Н₁₁постоянно, это диф­ференциальное уравнение легко решается, давая

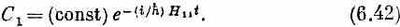
Так зависит от времени состояние с определенной энергией Е=Н₁₁. Вы видите, почему Н_ijследовало бы называть энер­гетической матрицей: она обобщает понятие энергии на бо­лее сложные случаи.

Вслед за этим, чтобы еще лучше разобраться в смысле уравнений, рассмотрим систему с двумя базисными состояниями.

Тогда (6.39) читается так:

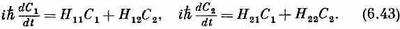
Если все Н опять не зависят от времени, то эти уравнения легко решить. Для интереса займитесь этим сами, а мы позже еще вернемся к ним. Вот вы уже и можете вести расчеты по кван­товой механике, зная об Н только то, что оно не зависит от времени!

§ 6. Молекула аммиака

Теперь мы хотим продемонстрировать, как динамическое уравнение квантовой механики может быть использовано для описания какой-то физической обстановки. Мы выбрали ин­тересный и простой пример, в котором, сделав некоторые ра­зумные предположения о гамильтониане, сможем вывести кое-какие важные (и даже практически важные) результаты. Возьмем случай, когда достаточно двух состояний,— это мо­лекула аммиака.

Молекулу аммиака образуют один атом азота и три атома водорода, плоскость которых проходит мимо атома азота, так что молекула имеет форму пирамидки (фиг. 6.1, а).

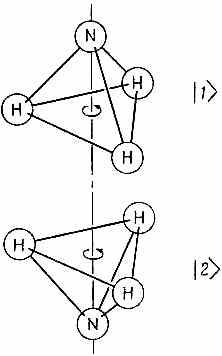
Фиг. 6.I. Два равноценных геометрических расположения молекулы аммиака.

Эта мо­лекула, как и всякая другая, обладает бесконечным количест­вом состояний. Она может вращаться вокруг какой угодно оси; двигаться в любом направлении, вибрировать и т. д. и т. п. Значит, это вовсе не система с двумя состояниями. Но мы сде­лаем следующее приближение: предположим, что все прочие степени свободы закреплены и не связаны с теми, которые нас сейчас интересуют. Будем считать, что молекула может только вращаться вокруг оси симметрии (как показано на рисунке), что импульс ее переносного движения равен нулю и что ее колебания очень слабы. Это фиксирует все условия, кроме одного: для, атома азота все еще существуют два возможных положения — он может оказаться по одну сторону плоскости атомов водорода, а может оказаться и по другую (фиг. 6.1). Так что мы будем рассуждать о молекуле, как если бы она была системой с двумя состояниями. Под этим подразумева­ется, что существуют только два состояния, о которых реально следует заботиться, все же прочее предполагается зафиксиро­ванным. Как видите, если даже известно, что молекула вращается вокруг оси с определенным моментом количества дви­жения и что она движется с определенным импульсом и колеб­лется определенным образом, то все равно еще остаются два Допустимых состояния. Будем говорить, что молекула нахо­дится в состоянии |1>, когда азот «вверху» (фиг. 6.1, а) и в состоянии |2>, когда азот «внизу» (фиг. 6.1, б). Состояния |1> и |2> в нашем анализе поведения молекулы аммиака можно принять за совокупность базисных состояний В каждый момент истинное состояние |y> молекулы может быть представлено заданием C₁=<1|y> — амплитуды пребывания в состоянии 1 и С₂=<2|y> — амплитуды пребывания в состоянии |2>. Тогда, используя (6.8), вектор состояния |y> можно записать так:

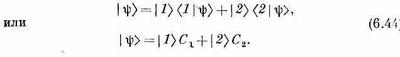
Но вот что интересно: если известно, что молекула в опреде­ленный момент была в определенном состоянии, то в следующий момент она может уже не быть в том же состоянии. Два С-коэффициента меняются со временем в соответствии с уравнениями (6.43), которые верны для любой системы с двумя состояниями. Предположим, к примеру, что вы сделали какое-то наблюде­ние (или как-то отобрали молекулы), так что знаете, что пер­воначально молекула находилась в состоянии |1>. Чуть позже уже появляются некоторые шансы засечь ее в состоянии |2>. Чтобы узнать, сколь велики эти шансы, нужно решить диф­ференциальное уравнение, которое говорит, как амплитуды меняются со временем.

Единственная трудность в том, что мы не знаем, что ставить вместо коэффициентов Н_ijв (6.43). Но кое-что мы все же можем сказать. Предположим, что, если уж молекула оказалась в со­стоянии 1 >, тогда у нее не будет никакого шанса когда-либо по­пасть в состояние |2>, И наоборот. Тогда H₁₂ и H₂₁ будут оба равны нулю, и (6.43) примет вид

Эти уравнения легко решить; получается

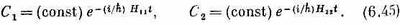
Это просто амплитуды стационарных состояний с энергиями E₁=H₁₁и E₂=H₂₂. Еще мы знаем, что у молекулы аммиака состояния |1>и |2>обладают определенной симметрией. Если природа ведет себя более или менее разумно, то матричные элементы Н₁₁и H₂₂должны равняться друг другу. Мы обозна­чим их через Е₀, потому что они соответствуют энергии, ко­торой обладали бы состояния, будь H₁₂ и H₂₁ равны нулю.

Но (6.45) не отражает того, что на самом деле бывает с аммиаком. Оказывается, что аммиак имеет возможность про­толкнуть свой азот мимо трех водородов и перебросить его по ту сторону. Это очень трудно: чтобы азоту пройти полпути, нужна немалая энергия. Как же он может пройти на другую сторону, если он не располагает достаточной энергией? Просто имеется некоторая амплитуда того, что он проникнет сквозь энергетический барьер. В квантовой механике разрешается быстро проскакивать через энергетически нелегальную об­ласть. Стало быть, существует небольшая амплитуда того, что молекула, начав с состояния |1>, перейдет в состояние |2>. Коэффициенты Н₁₂и Н₂₁на самом деле не равны нулю. И опять из симметрии ясно, что они должны быть одинаковы, по край­ней мере по величине. И действительно, мы уже знаем, что вообще Н_ijравняется комплексно сопряженной величине Н_ji, т. е, они могут отличаться только фазой. Оказывается, как вы потом увидите, что без потери общности можно положить эти коэффициенты равными друг другу. Позднее нам будет удоб­нее считать их равными отрицательному числу; мы примем поэтому H₁₂=H₂₁=-А. Тогда получится следующая пара уравнений:

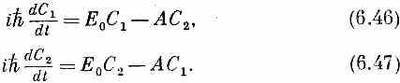
Эти уравнения достаточно просты и могут быть решены разным путем. Удобно решать их так. Складывая их, по­лучаем

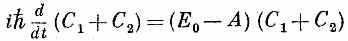
с решением

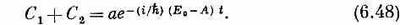
Вычитая затем (6.47) из (6.46), получаем

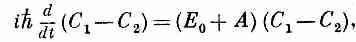
что дает

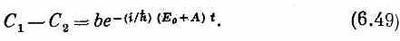
Две постоянные интегрирования мы обозначили а и b; их надо выбрать так, чтобы получились подходящие начальные условия данной физической задачи. Наконец, складывая и вычитая (6.48) и (6.49), получаем C₁и С₂:

Они отличаются только знаком при втором слагаемом.

Решения-то мы получили, но что они значат? (В квантовой механике трудность не только в том, чтобы получить решения но и в том, чтобы разобраться в их смысле!) Заметьте, что при b=0оба решения обладают одинаковой частотой w=(E₀-A)/h Если все меняется с одной частотой, это значит, что система пребывает в состоянии с определенной энергией, в данном слу­чае с энергией (Е₀-А). Значит, существует стационарное состояние с такой энергией; в нем обе амплитуды С₁и C₂равны друг другу. Мы приходим к выводу, что молекула аммиака обладает определенной энергией (Е₀-А), если для атома азота одинакова амплитуда оказаться «вверху» и «внизу».

Имеется другое допустимое стационарное состояние, когда а=0; тогда обе амплитуды обладают частотой (E₀+A)/h. Зна­чит, имеется другое состояние с определенной энергией (Е₀+А), когда две амплитуды равны, но отличаются знаком: C₂=-C₁. Вот и все состояния с определенной энергией. В следующей главе мы поговорим о состояниях молекулы аммиака подроб­нее; здесь же мы отметим еще только некоторые особенности.

Мы приходим к заключению, что из-за того, что имеется некоторая вероятность перескока атома азота из одного по­ложения в другое, энергия молекулы равна не просто Е₀, как можно было ожидать, но обладает двумя энергетическими уровнями (Е₀+А)и (Е₀-А). Каждое из возможных состояний молекулы, какую бы энергию оно ни имело, «расщепляется» на два уровня. Мы говорим «каждое из состояний», потому что, как вы помните, мы выбрали какое-то определенное состояние вращения с определенной внутренней энергией и т. д. И для каждых мыслимых условий подобного рода возникает (из-за возможности переворота молекулы) пара энергетических уров­ней.

Теперь поставим следующий вопрос. Пусть мы знаем, что при t=0молекула находится в состоянии |1>, т. е. что С₁{0)=1 и С₂(0)=0. Какова вероятность того, что молекула будет обна­ружена в момент t в состоянии |2> или же что она окажется в этот момент в состоянии |1>? Наши начальные условия го­ворят нам, какими должны быть а и b в (6.50) и (6.51). Полагая t=0, имеем

Значит, а=b=1. Подставляя их в формулы для С₁(t) и С₂(t) и вынося общий множитель, получаем

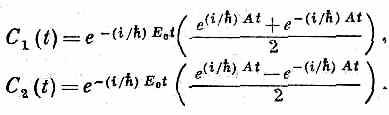
Это можно переписать так:

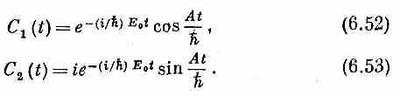
Величина обеих амплитуд гармонически изменяется во времени. Вероятность того, что молекула будет обнаружена в со­стоянии |2> в момент t, равна квадрату модуля C₂(t):

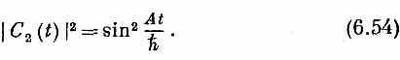
Она, как и следует, начинается с нуля, растет до единицы и затем колеблется вперед и назад между нулем и единицей, как показано на кривой, обозначенной P₂, на фиг. 6.2.

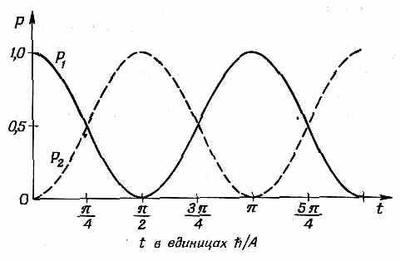
Фиг. 6.2. p₁— вероятность того, что молекула аммиака, находившаяся при t=0 в состоянии |1>, бу­дет обнаружена в момент t тоже в состоянии |1>; Р₂— вероятность того, что она будет обнаружена в состоянии |2>.

Вероят­ность остаться в состоянии |1> тоже, конечно, не остается равной единице. Она «перекачивается» во второе состояние до тех пор, пока вероятность увидать молекулу в первом состоя­нии не обратится в нуль, как показано на кривой Р₁фиг. 6.2. Вероятность попросту переливается туда и обратно между этими двумя состояниями.

Еще раньше мы видели, что бывает, если качаются два одинаковых маятника, слегка связанные друг с другом [см. гл.49 (вып.4)]. Когда мы отводим в сторону один из них и отпускаем, он колеблется, но затем постепенно начинает колебаться дру­гой и вскоре забирает себе всю энергию. Затем процесс обра­щается, и энергию отбирает первый маятник. В точности то же самое происходит и здесь. Скорость, с какой происходит обмен энергией (быстрота просачивания «колебаний»), зависит от связи между маятниками. Кроме того, как вы помните, при двух маятниках существуют два определенных типа движений (каждый с определенной частотой), которые мы назвали фун­даментальными типами колебаний. Если отклонить оба маят­ника вместе, они колеблются с одной частотой. Если же отклонить один в одну сторону, а другой — в другую, то появляется иной стационарный тип колебаний и тоже с определенной частотой. С тем же мы встретились и сейчас — молекула аммиака математически походит на пару маятников. Существуют две частоты (E₀+A)/h и (Е₀-A)/h, при которых они колеблются либо разом, либо навстречу друг другу.

Сходство с маятником ненамного глубже принципа, что у оди­наковых уравнений и решения одинаковы. Линейные уравнения для амплитуд (6.39) очень похожи на линейные уравнения для гармонических осцилляторов. (В действительности именно этой причине обязана успехом наша классическая теория пока­зателя преломления, в которой квантовомеханический атом мы заменяли гармоническим осциллятором, хотя классически неразумно говорить об электронах, циркулирующих вокруг ядра.) Толкнув атом азота в одну сторону, вы получите супер­позицию этих двух колебаний и тем самым своеобразные бие­ния, потому что система не будет находиться в том или ином состоянии с определенной частотой. Однако расщепление уров­ней энергии молекулы аммиака — это строго квантовомеханический эффект.

Расщепление уровней энергии молекулы аммиака имеет важные практические применения, которые мы опишем в сле­дующей главе. Наконец-то у нас будет пример практической физической задачи, которую мы сможем понять при помощи квантовой механики!

* Здесь небольшая неприятность с обозначениями. В этом множителе i означает мнимую единицу Ц-1, а не индекс i, относящийся к i-му базисному состоянию! Надеемся, это не слишком смутит вас.

* Вы можете оказать, что надо писать не просто А, но |А|. Но тогда это будет похоже на символ «абсолютного значения А». Поэтому обычно черточки опускают. Черточка (|) вообще ведет себя очень похоже на множитель единица.