Глава 1 АМПЛИТУДЫ ВЕРОЯТНОСТИ

We use cookies. Read the Privacy and Cookie Policy

Глава 1

АМПЛИТУДЫ ВЕРОЯТНОСТИ

§ 1.Законы композиции амплитуд

§ 2.Картина интерференции от двух щелей

§ З. Рассеяние на кристалле

§ 4. Тождественные частицы

Повторить:гл. 37 (вып. 3) «Кван­товое поведение» ; гл. 38 (вып. 3) « Соотношение между волновой и корпускулярной точками зрения»

§ 1. Законы композиции амплитуд

Когда Шредингер впервые открыл правиль­ные законы квантовой механики, он написал уравнение, которое описывало амплитуду ве­роятности обнаружения частицы в различ­ных местах. Это уравнение было очень похоже на уравнения, которые были уже изве­стны классическим физикам, они ими пользо­вались, чтобы описать движение воздуха в звуковой волне, распространение света и т. д. Так что в начале развития квантовой механики большую часть времени люди занимались ре­шением этого уравнения. Но в то же время началось (в частности, благодаря Борну и Дираку) понимание тех фундаментально новых идей, которые лежали в основе кванто­вой механики. По мере дальнейшего ее разви­тия выяснилось, что в ней есть много такого, что прямо в уравнении Шредингера не содер­жится,— таких вещей, как спин электрона и различные релятивистские явления. Все курсы квантовой механики по традиции начинают с того же самого, повторяя путь, пройденный в историческом развитии предмета. Сперва долго изучают классическую механику, чтобы потом понять, как решается уравнение Шредингера. Затем столь же долго получают различные решения. И лишь после деталь­ного изучения этого уравнения переходят к «высшим» вопросам, таким, как спин электрона.

Сначала мы тоже считали, что лучше всего закончить эти лекции, показав, как решаются уравнения классической физики в различных сложных случаях, таких, как опи­сание звуковых волн в замкнутом пространстве, типы элек­тромагнитного излучения в цилиндрических полостях и т. д. Таков был первоначальный план этого курса. Но затем мы решили отказаться от этого плана и вместо этого дать введение в квантовую механику. Мы пришли к заключе­нию, что то, что обычно именуют «высшими» разделами квантовой механики, на самом деле совсем простая вещь. Нужная для этого математика чрезвычайно проста — требуются лишь несложные алгебраические операции, никаких дифферен­циальных уравнений не нужно (или в крайнем случае нужны самые простые). Проблема только в том, чтобы перепрыгнуть через одно препятствие: усвоить, что мы больше не имеем права детально описывать поведение частиц в пространстве. И вот этим-то мы и собираемся заняться: рассказать вам о том, что обычно называют «высшими» разделами квантовой механики. Но уверяю вас, это самые что ни на есть простые (в полном смысле этого слова), но в то же время самые фундаментальные ее части. Честно говоря, это педагогический эксперимент, и, насколько нам известно, он никогда раньше не ставился.

Конечно, здесь есть своя трудность: квантовомеханическое поведение вещей чрезвычайно странно. Никто не может пола­гаться на то, что его ежедневный опыт даст ему интуитивное, грубое представление о том, что должно произойти. Так что этот предмет можно представить двояким образом: можно либо довольно грубо , описать, что происходит — сообщать более или менее подробно, что случится, но не формулировать точных законов, либо же можно приводить и точные законы в их абстрактном виде. Но тогда эта абстракция приведет к тому, что вы не будете знать, к чему физически она относится. Этот способ не годится, потому что он совершенно отвлеченный, а от первого способа будет оставаться неприятный осадок, потому что никогда не будет точно известно, что верно, а что нет. И мы не знаем, как эту трудность обойти. С этой проблемой мы уже сталкивались раньше [гл. 37 и 38 (вып. 3)1. В гл. 37 изложение относительно строгое, а в гл. 38 дано лишь грубое описание раз­личных явлений. Теперь мы попытаемся найти золотую сере­дину.

Мы начнем эту главу с некоторых общих квантовомеханических представлений. Кое-какие из этих утверждений будут со­вершенно точными, иные же точны лишь частично. При изложении нам будет трудно отмечать, которые из них какие, но к тому времени, когда вы дочитаете книжку до конца, вы уже сами будете понимать, оглядываясь назад, какие части устояли, а какие оказались только грубым объяснением. Главы, которые последуют за этой, не будут столь неточными. Одна из причин, почему мы пытаемся в последующих главах быть как можно более точными, состоит в том, что таким образом мы сможем продемонстрировать одно из самых прекрасных свойств кван­товой механики — как много в ней удается вывести из столь малого.

Мы опять начинаем с выяснения свойств суперпозиции, наложения, амплитуд вероятностей. Для примера мы сошлем­ся на опыт, описанный в гл. 37 (вып. 3) и еще раз показанный здесь на фиг. 1.1.

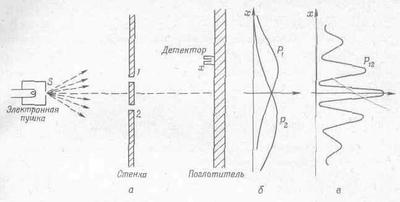
Фиг. 1.1. Интерференционный опыт с электронами.

Имеется источник частиц s, скажем электронов; дальше стоит стенка, в которой имеются две щели; за стенкой помещен детектор; он находится где-то в точке х. Мы спраши­ваем: какова вероятность того, что в точке х будет обнаружена частица? Наш первый общий принцип квантовой механики заключается в том, что вероятность того, что частица достигнет точки х, выйдя из источника s, может быть численно представле­на квадратом модуля комплексного числа, называемого ампли­тудой вероятности, в нашем случае — «амплитудой того, что частица из s попадет в х». К этим амплитудам мы будем прибе­гать так часто, что удобно будет использовать сокращенное обозначение, изобретенное Дираком и повсеместно применяемое в квантовой механике, чтобы отображать это понятие. Мы запишем амплитуду вероятности так:

<Частица попадает в х|Частица покидает s> (1.1)

Иными словами, две скобки <> — это знак, эквивалентный словам «амплитуда (вероятности) того, что»; выражение справа от вертикальной черточки всегда задает начальное условие, а то, что слева,— конечное условие. А иногда будет удобно еще сильнее сокращать, описывая начальные и конечные условия одной буквой. Например, амплитуду (1.1) можно при случав записать и так:

<x|s>. (1.2)

Надо подчеркнуть, что подобная амплитуда — это, конечно, всего-навсего число — комплексное число.

В гл. 37 (вып. 3) мы уже видели, что, когда частица может достичь детектора двумя путями, итоговая вероятность не есть сумма двух вероятностей, а должна быть записана в виде квад­рата модуля суммы двух амплитуд. Мы обнаружили, что ве­роятность того, что электрон достигнет детектора при обеих открытых амбразурах, есть

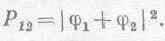(1.3)

Теперь мы этот результат собираемся записать в наших новых обозначениях. Сначала сформулируем наш второй общий принцип квантовой механики. Когда частица может достичь данного состояния двумя возможными путями, полная амплиту­да процесса есть сумма амплитуд для этих двух путей, рас­сматриваемых порознь. В наших новых обозначениях мы на­пишем

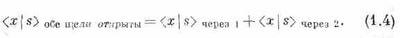
При этом мы предполагаем, что щели 1 и 2 достаточно малы, так что, когда мы говорим, что электрон прошел сквозь щель, не встает вопрос, через какую часть щели он прошел. Конечно, можно разбить каждую щель на участки с конечной амплитудой того, что электрон прошел через верх щели или через низ и т. д. Мы допустим, что щель достаточно мала, так что нам не надо думать об этой детали. Это одна из тех неточностей, о которых мы говорили; суть дела можно уточнить, но мы покамест не будем этого делать.

Теперь мы хотим подробнее расписать, что можно сказать об амплитуде процесса, в котором электрон достигает детектора в точке х через щель 1. Это можно сделать, применив третий общий принцип. Когда частица идет каким-то определенным данным путем, то амплитуда для этого пути может быть записана в виде произведения амплитуды того, что будет пройдена часть пути, на амплитуду того, что и остаток пути будет пройден.

Для установки, показанной на фиг. 1.1, амплитуда перехода от s к х сквозь щель 1 равна амплитуде перехода от s к 1, умно­женной на амплитуду перехода от 1 к х:

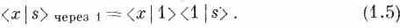
Опять-таки, это утверждение не совсем точно. Нужно добавить еще один множитель — амплитуду того, что электрон пройдет щель в точке 1; но пока это у нас просто щель, и мы положим упомянутый множитель равным единице.

Заметьте, что уравнение (1.5) кажется написанным задом наперед. Его надо читать справа налево: электрон переходит от s к 1 и затем от 1 к х. В итоге если события происходят друг за другом, т. е. если вы способны проанализировать один из путей частицы, говоря, что она сперва делает то-то, затем то-то, потом то-то, то итоговая амплитуда для этого пути вы­числяется последовательным умножением на амплитуду каж­дого последующего события. Пользуясь этим законом, мы мо­жем уравнение (1.4) переписать так:

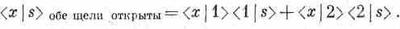
А теперь мы покажем, что, используя одни только эти прин­ципы, уже можно решать и более трудные задачи, наподобие показанной на фиг. 1.2.

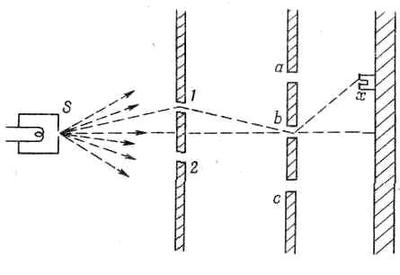
Фиг. 1.2. Интерференционный опыт посложнее.

Тут изображены две стенки: одна с двумя щелями 1 и 2, другая с тремя — а, b и с. За второй стенкой в точке х стоит детектор, и мы хотим узнать амплитуду того, что частица достигнет х. Один способ решения состоит в расчете суперпозиции, или интерференции, волн, проходящих сквозь щели; но можно сделать и иначе, сказав, что имеется шесть возможных путей, и накладывая друг на друга их амплитуды. Электрон может пройти через щель 1, затем через щель а и потом в х, или же он мог бы пройти сквозь щель 1, затем сквозь щель b и затем в x; и т. д. Согласно нашему второму принципу, амплитуды взаимоисключающих путей складываются, так что мы должны записать амплитуду перехода от s к х в виде суммы шести отдельных амплитуд. С другой стороны, согласно третье­му принципу, каждую из них можно записать в виде произведе­ния трех амплитуд. Например, одна из них — это амплитуда перехода от s к 1, умноженная на амплитуду перехода от 1 к а и на амплитуду перехода от а к я. Используя наше сокращенное обозначение, полную амплитуду перехода от s к х можно запи­сать в виде

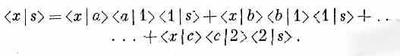
Можно сэкономить место, использовав знак суммы:

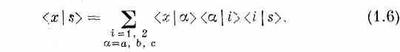
Чтобы, пользуясь этим методом, проводить какие-то вы­числения, надо, естественно, знать амплитуду перехода из од­ного места в другое. Я приведу пример типичной амплитуды. В ней не учтены некоторые детали, такие, как поляризация све­та или спин электрона, а в остальном она абсолютно точна. С ее помощью вы сможете решать задачи, куда входят различные сочетания щелей. Предположим, что частица с определенной энергией переходит в пустом пространстве из положения r1 в положение r2. Иными словами, это свободная частица: на нее не действуют никакие силы. Отбрасывая численный множитель впереди, амплитуду перехода от r1 к r2 можно записать так:

где r12=r2-r1 а р — импульс частицы, связанный с ее энергией Е релятивистским уравнением

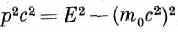
или нерелятивистским уравнением

p2/2m = Кинетическая энергия.

Уравнение (1.7) в итоге утверждает, что у частицы есть волно­вые свойства, что амплитуда распространяется как волна с волновым числом, равным импульсу, деленному на

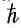
В общем случае в амплитуду и в соответствующую вероят­ность входит также и время. В большинстве наших первона­чальных рассуждений будет предполагаться, что источник испускает частицы с данной энергией беспрерывно, так что о времени не нужно будет думать. Но, вообще-то говоря, мы вправе заинтересоваться и другими вопросами. Допустим, что частица испущена в некотором месте Р в некоторый момент и вы хотите знать амплитуду того, что она окажется в каком-то месте, скажем г, в более позднее время. Это символически мож­но представить в виде амплитуды <r, t = t1 P, t= 0>. И яс­но, что она зависит и от r, и от t. Помещая детектор в разные места и делая измерения в разные моменты времени, вы получите разные результаты. Эта функция r и t, вообще говоря, удовле­творяет дифференциальному уравнению, которое является волно­вым уравнением. Скажем, в нерелятивистском случае это уравне­ние Шредингера. Получается волновое уравнение, аналогичное уравнению для электромагнитных волн или звуковых волн в газе. Однако надо подчеркнуть, что волновая функция, удовлет­воряющая уравнению, не похожа на реальную волну в простран­стве; с этой волной нельзя связать никакой реальности, как это делается со звуковой волной.

Хотя, имея дело с одной частицей, можно начать пытаться мыслить на языке «корпускулярных волн», но ничего в этом хорошего нет, потому что если, скажем, частиц не одна, а две, то амплитуда обнаружить одну из них в r1 а другую в r2 не есть обычная волна в трехмерном пространстве, а зависит от шести пространственных переменных r1и r2. Когда частиц две (или больше), возникает потребность в следующем добавочном прин­ципе. Если две частицы не взаимодействуют, то амплитуда того, что одна частица совершит что-то одно, а другая сделает что-то другое, есть произведение двух амплитуд — амплитуд того, что две частицы проделали бы это по отдельности. Напри­мер, если <а|s1>есть амплитуда того, что частица 1 перейдет из s1 в а, а <b|s2> — амплитуда того, что частица 2 перейдет из s2 в b, то амплитуда того, что оба эти события произойдут вместе, есть

<a|sl><b|s2>.

И еще одну вещь надо подчеркнуть. Предположим, нам не­известно, откуда появляются частицы на фиг. 1.2, прежде чем они пройдут через щели 1 и 2 в первой стенке. Несмотря на это, мы все равно можем предсказать, что произойдет за стенкой (скажем, вычислить амплитуду попасть в х), если только нам даны два числа: амплитуда попадания в 1 и амплитуда попада­ния в 2. Иными словами, из-за того, что амплитуды последова­тельных событий перемножаются, как это показано в уравнении (1.6), все, что вам нужно знать для продолжения анализа,— это два числа, в данном частном случае <1|s> и <2|s>. Этих двух комплексных чисел достаточно для того, чтобы предска­зать все будущее. Это-то и делает квантовую механику простой. В следующих главах выяснится, что именно это мы и делаем, когда отмечаем начальные условия при помощи двух (или нескольких) чисел. Конечно, эти числа зависят от того, где рас­положен источник и каковы другие свойства прибора, но, как только эти числа даны, все подобные детали нам больше не нужны.

§ 2. Картина интерференции от двух щелей

Рассмотрим еще раз вопрос, который мы довольно подробно обсудили раньше, в гл. 37 (вып. 3). Сейчас мы используем идею об амплитуде во всей ее мощи, чтобы показать вам, как она работает. Вернемся к старому опыту, изображенному на фиг. 1.1, добавив к нему еще источник света и поместив его за щелями (ср. фиг. 37.4 гл. 37). В гл. 37 мы обнаружили следующий приме­чательный результат. Если мы заглядывали за щель 1 и заме­чали фотоны, рассеивавшиеся где-то за ней, то распределение вероятности того, что электрон попадал в х при одновременном наблюдении этих фотонов, было в точности такое же, как если бы щель 2 была закрыта. Суммарное распределение для элект­ронов, которые были «замечены» либо у щели 1, либо у щели 2, было суммой отдельных распределений и было совсем не похоже на распределение, которое получалось, когда свет бывал вы­ключен. По крайней мере так бывало, когда использовался свет с малой длиной волн. Когда длина волны начинала расти и у нас исчезала уверенность в том, у какой из щелей произо­шло рассеяние света, распределение становилось похожим на то, которое бывало при выключенном свете.

Посмотрим теперь, что здесь происходит, используя наши новые обозначения и принципы композиции амплитуд. Чтобы упростить запись, можно через j1опять обозначить амплитуду того, что электрон придет в х через щель 1, т. е.

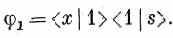
Сходным же образом j2 будет обозначать амплитуду того, что электрон достигнет детектора через щель 2:

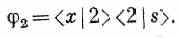
Это — амплитуды проникновения электрона через щель и появле­ния в х, когда света нет. А если свет включен, мы поставим себе вопрос: какова амплитуда процесса, в котором вначале электрон выходит из s, а фотон испускается источником света L, а в конце электрон оказывается в ж, а фотон обнаруживается у щели 1? Предположим, что мы с помощью счетчика D1наблюдаем фотон у щели 1 (фиг. 1.3), а такой же счетчик D2 считает фо­тоны, рассеянные у щели 2.

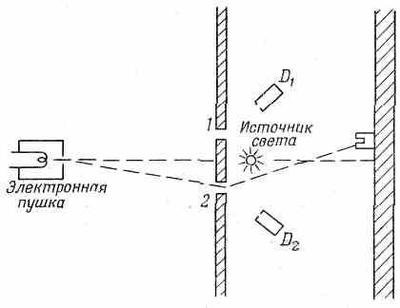
Фиг.1.3. Опыт, в котором определяется, через которую из щелей проник электрон.

Тогда можно говорить об ампли­туде появления фотона в счетчике D1а электрона в x; и об амплитуде появления фотона в счетчике D2, а электрона в х. Попробуем их подсчитать.

Хоть мы и не располагаем правильной математической формулой для всех множителей, входящих в этот расчет, но дух расчета вы почувствуете из следующих рассуждений. Во-первых, имеется амплитуда <1|s> того, что электрон доходит от источника к щели 1. Затем можно предположить, что имеется конечная амплитуда того, что, когда электрон находится у щели 1, он рассеивает фотон в счетчик D1. Обозначим эту ам­плитуду через а. Затем имеется амплитуда <x|1> того, что электрон переходит от щели 1 к электронному счетчику в х. Амплитуда того, что электрон перейдет от s к х через щель 1 ирассеет фотон в счетчик D1тогда равна

<x|l> a <l|s>.

Или в наших прежних обозначениях это просто аj1.

Имеется также некоторая амплитуда того, что электрон, проходя сквозь щель 2, рассеет фотон в счетчик D1. Вы скажете: «Это невозможно; как он может рассеяться в счетчик D1? если тот смотрит прямо в щель 1?» Если длина волны достаточно велика, появляются дифракционные эффекты, и это становится возможным. Конечно, если прибор будет собран хорошо и если используются лишь фотоны с короткой длиной волны, то ам­плитуда того, что фотон рассеется в счетчик D1от электрона в щели 2, станет очень маленькой. Но для общности рассуждения мы учтем тот факт, что такая амплитуда всегда имеется, и обо­значим ее через b. Тогда амплитуда того, что электрон проходит через щель 2 и рассеивает фотон в счетчик D1есть

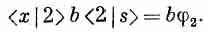
Амплитуда обнаружения электрона в х и фотона в счетчике D1 есть сумма двух слагаемых, по одному для каждого мысли­мого пути электрона. Каждое из них в свою очередь составлено из двух множителей: первого, выражающего, что электрон прошел сквозь щель, и второго — что фотон рассеян таким электроном в счетчик D1;мы имеем

Аналогичное выражение можно получить и для случая, ког­да фотон будет обнаружен другим счетчиком D2. Если допус­тить для простоты, что система симметрична, то а будет также амплитудой попадания фотона в счетчик D2, когда электрон проскакивает через щель 2, a b — амплитудой попадания фо­тона в счетчик D2, когда электрон проходит через щель 1. Соот­ветствующая полная амплитуда — амплитуда того, что фотон окажется в счетчике D2, а электрон в х,— равна

Вот и все. Теперь мы легко можем рассчитать вероятность тех или иных случаев. Скажем, мы желаем знать, с какой ве­роятностью будут получаться отсчеты в счетчике D1при попада­нии электрона в х. Это будет квадрат модуля амплитуды, давае­мой формулой (1.8), т. е. попросту |aj1+bj2|2. Поглядим на это выражение внимательнее. Прежде всего, если b=0 (мы хотели бы, чтобы наш прибор работал именно так), ответ просто равен |j1|2 с множителем |a|2. Это как раз то рас­пределение вероятностей, которое получилось бы при наличии лишь одной щели, как показано на фиг. 1.4, а.

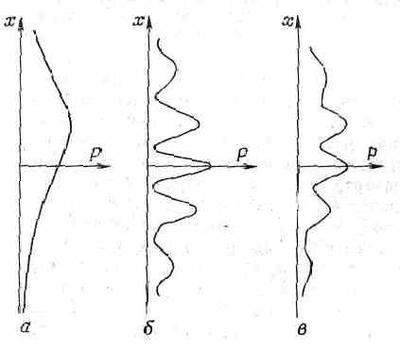
Фиг. 1.4. Вероятность отсчета электрона в х при условии, что в D1 замечен фотон в опыте, показанном на фиг. 1.3. а — при b=0; б — при b=а; в — при 0<b<а.

С другой сторо­ны, если длина волны велика, рассеяние за щелью 2 в счетчик D1 может стать почти таким же, как за щелью 1. Хотя в а и b могут входить какие-то фазы, возьмем самый простой случай, когда обе фазы одинаковы. Если а практически совпадает с b, то полная вероятность обращается в | j1+j2|2, умноженное на |а|2, потому что общий множитель а можно вынести. Но тогда выходит то самое распределение вероятностей, которое получилось бы, если бы фотонов вовсе не было. Следовательно, когда длина волны очень велика (и детектировать фотоны бес­полезно), вы возвращаетесь к первоначальной кривой распре­деления, на которой видны интерференционные эффекты, как показано на фиг. 1.4,б. Когда же детектирование частично все же оказывается эффективным, возникает интерференция между большим количеством j1 и малым количеством j2 и вы получаете промежуточное распределение, такое, какое намечено на фиг. 1.4,в. Само собой разумеется, если нас заинтересуют одно­временные отсчеты фотонов в счетчике D2 и электронов в х, то мы получим тот же результат. Если вы вспомните рассужде­ния гл. 37 (вып. 3), то увидите, что эти результаты описывают количественно то, что было сказано там.

Нам хотелось бы подчеркнуть очень важное обстоятельство и предостеречь от часто допускаемой ошибки. Пусть вас инте­ресует только амплитуда того, что электрон попадает в х, причем вам безразлично, в какой счетчик попал фотон — в D1или в D2. Должны ли вы складывать амплитуды (1.8) и (1.9)? Нет! Никог­да не складывайте амплитуды разных, отличных друг от друга конечных состояний. Как только фотон был воспринят одним из фотонных счетчиков, мы всегда, если надо, можем узнать, не возмущая больше системы, какая из альтернатив (взаимо­исключающих событий) реализовалась. У каждой альтерна­тивы есть своя вероятность, полностью независимая от другой. Повторяем, не складывайте амплитуд для различных конечных условий (под «конечным» мы понимаем тот момент, когда нас интересует вероятность, т. е. когда опыт «закончен»). Зато нужно складывать амплитуды для различных неразличимых альтернатив в ходе самого опыта, прежде чем целиком закон­чится процесс. В конце процесса вы можете, если хотите, ска­зать, что вы «не желаете смотреть на фотон». Это ваше личное дело, но все же амплитуды складывать нельзя. Природа не знает, на что вы смотрите, на что нет, она ведет себя так, как ей положено, и ей безразлично, интересуют ли вас ее данные или нет. Так что мы не должны складывать амплитуды. Мы сперва возводим в квадрат модули амплитуд для всех возможных разных конечных состояний, а затем уж складываем. Пра­вильный результат для электрона в x и фотона то ли в D1то ли в D2 таков:

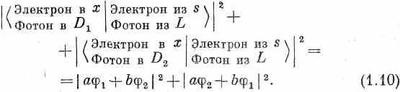
§ 3. Рассеяние на кристалле

Следующий пример — это явление, в котором интерферен­цию амплитуд вероятности следует проанализировать тщатель­нее. Речь идет о процессе рассеяния нейтронов на кристалле. Пусть имеется кристалл, в котором много атомов, а в центре каждого атома — ядро; ядра расположены периодически, и откуда-то издалека на них налетает пучок нейтронов. Различ­ные ядра в кристалле можно пронумеровать индексом i, где i пробегает целые значения 1, 2, 3, ... , N, а N равняется общему числу атомов. Задача состоит в том, чтобы подсчитать вероят­ность того, что нейтрон окажется в счетчике, изображенном на фиг. 1.5.

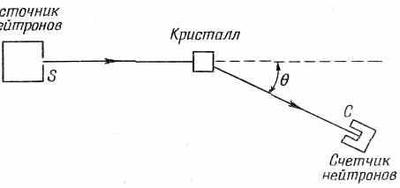
Фиг. 1.5. Измерение рассеяния нейтронов на кристалле.

Для каждого отдельного атома i амплитуда того, что нейтрон достигнет счетчика С, равна амплитуде того, что нейтрон из источника S попадет в ядро i, умноженной на ампли­туду а рассеяния в этом месте и умноженной на амплитуду того, что он из i попадет в счетчик С. Давайте запишем это:

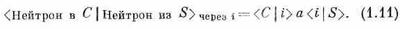
Написав это, мы предположили, что амплитуда рассеяния а — одна и та же для всех атомов. Здесь у нас есть множество, по-видимому, неразличимых путей. Они неразличимы оттого, что нейтрон с небольшой энергией рассеивается на ядре, не выбивая при этом самого атома с его места в кристалле — никакой «отметки» о рассеянии не остается. Согласно нашим прежним рассуждениям, полная амплитуда того, что нейтрон попал в С, включает в себя сумму выражения (1.11) по всем атомам:

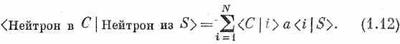
Из-за того, что складываются амплитуды рассеяния на ато­мах, по-разному расположенных в пространстве, у амплитуд будут разные фазы, и это даст характерную интерференционную картину, которую мы уже анализировали на примере рассеяния света на решетке.

Интенсивность нейтронов как функция угла в подобном опыте действительно ч часто обнаруживает сильнейшие изменения — очень острые интерференционные пики, между которы­ми ничего нет (фиг. 1.6, а).

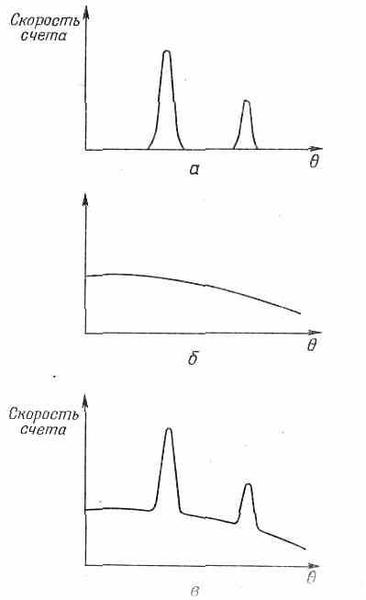
Фиг.1.6. Скорость счета нейтронов как функция угла, а — для ядер со спином 0; б — вероятность рассеяния с перево­ротом спина; в — наблюдаемая скорость счета для ядра со спи­ном 1/2.

Однако в некоторых сортах кристал­лов этого не случается, в них наряду с упомянутыми выше дифракционными пиками имеется общий фон от рассеяния во всех направлениях. Мы должны попытаться понять столь та­инственную с виду причину этого. Дело в том, что мы не учли одного важного свойства нейтрона. Его спин равен 1/2. и тем самым он может находиться в двух состояниях: либо его спин направлен вверх (скажем, поперек страницы на фиг. 1.5), либо вниз. И если у ядер самого кристалла спина нет, то спин нейтрона никакого действия не окажет. Но когда и у ядер кристалла есть спин, равный, скажем, тоже 1/2, то вы заметите фон от описанного выше размазанного рассеяния. Объяснение состоит в следующем.

Если спин нейтрона куда-то направлен и спин атомного ядра направлен туда же, то в процессе рассеяния направление спина не меняется. Если же спины нейтрона и атомного ядра направлены в противоположные стороны, то рассеяние может происходить посредством двух процессов, в одном из которых направления не меняются, а в другом происходит обмен направлениями. Это правило о том, что сумма спинов не должна меняться, аналогично нашему классическому закону сохране­ния момента количества движения. И мы уже в состоянии будем понять интересующее нас явление, если предположим, что все ядра, на которых происходит рассеяние, имеют одно и то же направление спина. Нейтрон с тем же направлением спина тогда рассеется так, что получится ожидавшееся узкое интерферен­ционное распределение. А что будет с нейтроном с противопо­ложным направлением спина? Если он рассеивается без пере­ворота направления спина, то ничего по сравнению со сказан­ным не меняется; но если при рассеянии оба спина перевора­чиваются, то, вообще говоря, можно указать, на каком из ядер произошло рассеяние, потому что именно у этого ядра спин перевернулся. Но если мы в состоянии указать, на каком атоме случилось рассеяние, то причем здесь остальные атомы? Ни при чем, конечно. Рассеяние здесь такое же, как от отдельного атома.

Чтобы учесть этот эффект, надо видоизменить математиче­скую формулировку уравнения (1.12), потому что в том анализе состояния не были охарактеризованы полностью. Пусть вна­чале у всех нейтронов, вылетающих из источника, спин направ­лен вверх, а у всех ядер кристалла — вниз. Во-первых, нам нужна амплитуда того, что в счетчике нейтронов их спин ока­жется направленным вверх и все спины в кристалле будут по-прежнему смотреть вниз. Это ничем не отличается от наших прежних рассуждений. Обозначим через а амплитуду рассея­ния без переворота спина. Амплитуда рассеяния от i-го атома, разумеется, равна

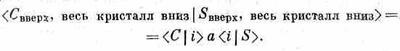
Поскольку все спины атомов направлены вниз, разные альтерна­тивы (разные значения i) нельзя друг от друга отличить. В этом процессе все амплитуды интерферируют.

Но есть и другой случай, когда спин детектируемого нейтро­на смотрит вниз, хотя вначале, в S, он смотрел вверх. Тогда в кристалле один из спинов должен перевернуться вверх, скажем спин k-го атома. Допустим, что у всех атомов амплитуда рас­сеяния с переворотом спина одна и та же и равна 6. (В реальном кристалле имеется еще одна неприятная возможность: пере­вернутый спин переходит к какому-то другому атому, но до­пустим, что в нашем кристалле вероятность этого мала.) Тогда амплитуда рассеяния равна

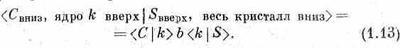
Если мы спросим теперь, какова вероятность того, что у нейтро­на спин окажется направленным вниз, а у k-го ядра — вверх, то она будет равняться квадрату модуля этой амплитуды, т. е. просто |b|2, умноженному на |<С|k><k|S>|2. Второй множитель почти не зависит от того, где атом k расположен в кристалле, и все фазы при вычислении квадрата модуля ис­чезают. Вероятность рассеяния на любом ядре кристалла с пере­воротом спина, стало быть, равна

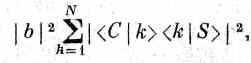
что дает гладкое распределение, как на фиг. 1.6, б.

Вы можете возразить: «А мне все равно, какой атом перевер­нулся». Пусть так, но природа-то это знает, и вероятность на самом деле выходит такой, как написано выше,— никакой интерференции не остается. А вот если вас заинтересует ве­роятность того, что спин в детекторе будет направлен вверх, а спины всех атомов — по-прежнему вниз, то вы должны будете взять квадрат модуля суммы:

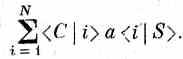
Поскольку у каждого слагаемого в этой сумме есть своя фаза, то они интерферируют и появляется резкая интерференционная картина. И если мы проводим эксперимент, в котором мы не наблюдаем спина детектируемого нейтрона, то могут произойти события обоих типов и сложатся отдельные вероятности. Полная вероятность (или скорость счета) как функция угла тогда выглядит подобно кривой на фиг. 1.6, в.

Давайте еще раз окинем взглядом физику этого опыта. Если вы способны в принципе различить взаимоисключающие ко­нечные состояния (хотя вы и не собирались на самом деле этого делать), то полная конечная вероятность получается подсчетом вероятности каждого состояния (а не амплитуды) и последую­щим их сложением. А если вы неспособны даже в принципе различить конечные состояния, тогда надо сперва сложить амплитуды вероятностей, а уж потом вычислять квадрат моду­ля и находить самую вероятность. Заметьте особенно, что если бы вы попытались представить нейтрон в виде отдельной волны, то получили бы одно и то же распределение и для рассеяния нейтронов, вращающихся спином вниз, и для нейтронов, вра­щающихся спином вверх. Вы должны были бы сказать, что «волна» нейтронов со спином, направленным вниз, пришла ото всех различных атомов и интерферирует так же, как это делает одинаковая по длине волна нейтронов со спином, направленным вверх. Но мы знаем, что на самом деле это не так. Так что (мы уже это отмечали) нужно быть осторожным и не представлять себе чересчур реально волны в пространстве. Они полезны для некоторых задач. Но не для всех.

§ 4. Тождественные частицы

Очередной опыт, который мы хотим описать, продемонстри­рует одно из замечательных следствий квантовой механики. В нем снова встретятся такие физические события, в которых существуют два неразличимых пути и, как всегда при таких об­стоятельствах, возникает интерференция амплитуд. Мы собира­емся рассмотреть рассеяние одних ядер на других при сравни­тельно низкой энергии. Начнем, скажем, с a-частиц (это, как вы знаете, просто ядра гелия), бомбардирующих кислород. Чтобы облегчить анализ реакции, проведем его в системе центра масс, в которой скорости ядра кислорода и a-частицы перед столкновением противоположны, а после столкновения тоже противоположны (фиг. 1.7, а). (Величины скоростей, конечно, различны, поскольку массы различны.) Предположим также, что энергия сохраняется и что энергия столкновения настолько мала, что частицы ни раскалываются, ни переходят в возбужденное состояние. Причина, отчего частицы отклоняют друг друга, состоит попросту в том, что обе они заряжены положительно и, выражаясь классически, отталкиваются, проходя одна мимо дру­гой. Рассеяние на разные углы будет происходить с различной вероятностью, и мы хотим выяснить угловую зависимость подоб­ного рассеяния. (Конечно, все это можно рассчитать классически, и по удивительной случайности оказалось, что ответ на этот вопрос в квантовой механике и в классической — один и тот же. Это очень занятно, потому что ни при каком законе сил, кроме закона обратных квадратов, так не бывает, стало быть, это и впрямь случайность.)

Вероятность рассеяния в разных направлениях можно из­мерить в опыте, изображенном на фиг. 1.7,а.

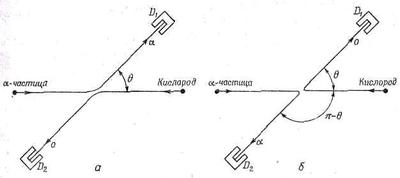
Фиг. 1.7. Рассеяние a-частиц на ядрах кислорода, наблюдаемое в системе центра масс.

Счетчик в положе­нии D1может быть сконструирован так, чтобы детектировать только a-частицы; счетчик в положении D2 может быть устроен так, чтобы детектировать кислород просто для проверки. (В си­стеме центра масс детекторы должны смотреть друг на друга, в лабораторной — нет.) Опыт заключается в измерении вероят­ности рассеяния в разных направлениях. Обозначим через f(q) амплитуду рассеяния в счетчики, когда они расположены под углом q; тогда | f(q)|2 — наша экспериментально опре­деляемая вероятность.

Можно было бы провести и другой опыт, в котором наши счетчики реагировали бы ина a-частицу, ина ядро кислорода. Тогда нужно сообразить, что будет, если мы решим не забо­титься о том, какая из частиц попала в счетчик. Разумеется, когда кислород летит в направлении q, то с противоположной стороны, под углом (p-q), должна оказаться a-частица (фиг. 1.7,б). Значит, если f(q) — амплитуда рассеяния кисло­рода на угол 0, то f(р-q) — это амплитуда рассеяния a-частицы на угол ?. Таким образом, вероятность того, что какая-то частица окажется в счетчике, который находится в положе­нии d1, равна

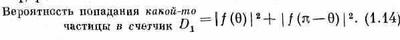
Заметьте, что в принципе оба состояния различимы. Даже если в этом опыте мы их не различали, мы могли бы это сделать. И в соответствии с нашими прежними рассуждениями мы, стало быть, должны складывать вероятности, а не амплитуды.

Приведенный выше результат справедлив для многих ядер. Мишенью здесь могут служить и кислород, и углерод, и бериллий, и водород. Но он неверен при рассеянии a-частиц на a-частицах. В том единственном случае, когда обе частицы в точности одинаковы, экспериментальные данные не согласуются с пред­сказаниями формулы (1.14). Например, вероятность рассеяния на угол 90° в точности вдвое больше предсказанной вышеизло­женной теорией — с частицами, являющимися ядрами «гелия», номер не проходит. Если мишень из Не3, а налетают на нее a-частицы (Не4), то все хорошо. И только когда мишень из Не4, т. е. ее ядра тождественны падающим a-частицам, только тогда рассеяние меняется с углом каким-то особым образом.

Быть может, вы уже догадались, в чем дело? В счетчике a-частица может очутиться по двум причинам: либо из-за рас­сеяния налетевшей a-частицы на угол q, либо из-за рассеяния ее на угол (p-q). Как мы можем удостовериться, кто попал в счетчик — частица-снаряд или частица-мишень? Никак. В случае рассеяния a-частиц на a-частицах существуют две альтернативы, различить которые нельзя. Приходится дать амплитудам вероятности интерферировать при помощи сложе­ния, и вероятность обнаружить в счетчике a-частицу есть квад­рат этой суммы:

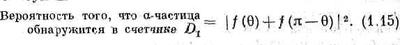
Это совсем не то, что (1.14). Возьмите, скажем, угол я/2 (это легче себе представить). При q=p/2 мы, естественно, имеем f(q)=f(p-q), так что из (1.15) вероятность оказывается равной

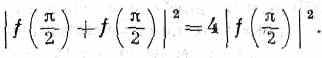
А с другой стороны, если бы не было интерференции, форму­ла (1.14) дала бы только 2|f(p/2)|2. Так что на угол 90° рас­сеивается вдвое больше частиц, чем можно было ожидать. Конечно, и под другими углами результаты будут другие. И мы приходим к необычному выводу: когда частицы тождественны, происходит нечто новое, чего не бывало, когда частицы можно было друг от друга отличить. При математическом описании вы обязаны складывать амплитуды взаимоисключающих процессов, в которых обе частицы просто обмениваются ролями, и происходит интерференция.

Еще более неожиданное явление происходит с рассеянием электронов на электронах или протонов на протонах. Тогда не верен ни один из прежних результатов! Для этих частиц мы должны призвать на помощь совершенно новое правило: если попадающий в некоторую точку электрон обменивается своей индивидуальностью с другим электроном, то новая ам­плитуда интерферирует со старой в противофазе. Это все равно интерференция, но с обратным знаком. В случае a-частиц, когда происходит обмен a-частицами, достигающими счетчика, амплитуды интерферируют с одним и тем же знаком. А в случае электронов амплитуды обмена интерферируют с разными зна­ками. С точностью до одной детали, о которой будет сейчас сказано, правильная формула для электронов в опыте, подобном изображенному на фиг. 1.8, такова:

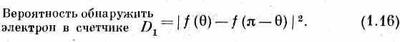
Это утверждение нуждается в уточнении, потому что мы не учли спин электрона (у a-частиц спина нет).

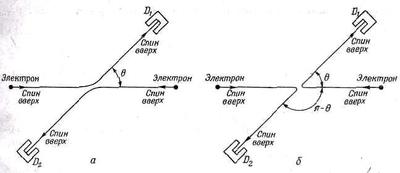
Фиг, 1.8. Рассеяние электронов на электронах.

Если спины сталкивающихся электронов параллельны, то процессы а и б неразличимы.

Спин электрона можно считать направленным либо вверх, либо вниз по отно­шению к плоскости рассеяния. Если энергия в опыте достаточно низка, то магнитные силы, возникающие от токов, будут ма­лы и не повлияют на спин. Предположим в нашем анализе, что так оно и есть, так что нет шансов, чтобы спины при столкно­вении перевернулись. Какой бы спин у электрона ни был, он уносит его с собой. Мы видим теперь, что есть много возможно­стей. У частицы-снаряда и частицы-мишени оба спина могут быть направлены вверх, или вниз, или в разные стороны. Если они оба направлены вверх, как на фиг. 1.8 (или оба — вниз), то после рассеяния останется то же самое, и амплитуда про­цесса будет разностью амплитуд тех двух возможностей, ко­торые показаны на фиг. 1.8. Вероятность обнаружить электрон в счетчике D1тогда будет даваться формулой (1.16).

Предположим, однако, что у «снаряда» спин направлен вверх, а у «мишени» — вниз. У электрона, попавшего в счетчик D1, спин может оказаться либо направленным вверх, либо —вниз, и, измеряя этот спин, мы можем сказать, выскочил ли этот элек­трон из бомбардирующего пучка или же из мишени.

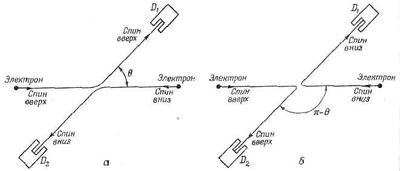
Фиг. 1.9. Рассеяние электронов с антипараллельными спинами.

Эти две возможности показаны на фиг. 1.9; в принципе они различимы, и поэтому интерференции не получится, просто сложатся две вероятности. Все это верно и тогда, когда оба первоначальных спина перевернуты, т. е. если спин слева смотрит вниз, а спин справа — вверх.

Таблица 1.1 · рассеяние неполяризованных частиц со спином 1/2

Наконец, если электроны вылетают случайно (например, они вылетают из накаленной вольфрамовой нити полностью неполяризованным пучком), то с равной вероятностью каждый отдельный электрон вылетит либо спином вверх, либо спином вниз. Если мы не собираемся в нашем опыте измерять в ка­кой-нибудь точке спин электронов, то получается то, что назы­вают экспериментом с неполяризованными частицами. Результат этого эксперимента лучше всего подсчитать, перечислив все мыс­лимые возможности, как это сделано в табл. 1.1. Для каждой различимой альтернативы отдельно подсчитана вероятность. Тогда полная вероятность есть сумма всех отдельных вероят­ностей. Заметьте, что для неполяризованных пучков результат при q=p/2 составляет половину классического результата для независимых частиц.

Поведение тождественных частиц приводит ко многим ин­тересным следствиям; в следующей главе мы обсудим их по­подробнее.

* Вообще-то направление рассеяния должно, конечно, описываться двумя углами — полярным углом j и азимутом q. Тогда следовало бы ска­зать, что рассеяние кислорода в направлении (q,j) означает, что a-частица движется в направлении (p-q, j+p). Однако для кулоновского рассеяния (и многих других случаев) амплитуда рассеяния не зависит от j. Тогда амплитуда того, что кислород полетел под углом 6, совпадает с ам­плитудой того, что a-частица полетела под углом (p-q).

* По-русски, наверно, правильнее говорить амплитуда вероятности, но короче говорить просто амплитуда и примириться с выражением типа «амплитуда того, что электрон находится в точке х».— Прим. ред.

* В американском издании этот том начинается с двух глав из второго тома [гл. 37 и 38 (вып. 3)], кото­рые авторы считали нужным повторить. Это было сде­лано для того, чтобы третий том можно было чи­тать, не обращаясь к прежним томам. В русском издании мы не стали печатать их снова: читатель должен всегда держать первые выпуски под рукой, поэтому нумерация глав в русском издании сдвинута на 2 единицы по сравнению с третьим томом. Из тех же соображений мы не перепечатали вновь гл. 34 и 35, они вошли в вып. 7.— Прим. ред.