4 ЗАГАДКА БЕЛЫХ КАРЛИКОВ

4

ЗАГАДКА БЕЛЫХ КАРЛИКОВ

глава, в которой Эддингтон и Чандрасекар ведут баталии вокруг смерти массивных звезд; должны ли они, погибая, схлопнуться, образуя черные дыры, или их спасет квантовая механика?

Год 1928-й, место действия — южная Индия, город Мадрас на берегу Бенгальского залива. Здесь, в Мадрасском университете, 17-летний индийский юноша Субраманьян Чандрасекар увлечен изучением физики, химии и математики. Чандрасекар — высокий и красивый юноша с царственными манерами — чрезвычайно горд своими академическими «успехами». Он только недавно прочитал классический учебник Арнольда Зоммерфельда «Атомные структуры и спектральные линии» и поэтому весьма обрадовался, узнав, что проживающий в Мюнхене Зоммерфельд — один из величайших в мире физиков-теоретиков — посетил Мадрас.

Сгорая от нетерпения, Чандрасекар отправился к Зоммерфельду в отель и попросил о встрече. Зоммерфельд назначил встречу на другой день. В указанное время гордый Чандрасекар, уверенный в своем владении основами современной физики, подошел к номеру Зоммерфельда в отеле и постучал в дверь. Зоммерфельд, вежливо поприветствовав пришедшего, осведомился об учебе, а затем развеял все его иллюзии. «Физика, которую Вы изучали, дело прошлого. Она полностью изменилась за те пять лет, что прошли с тех пор, как написана моя книга», — объяснил он. Зоммерфельд описал революцию в физическом понимании законов, которые управляют микромиром: миром атомов, молекул, электронов и протонов. В этом мире законы Ньютона, как было обнаружено, уже не справедливы, поскольку не выполняются принципы относительности движения. Им на смену пришел принципиально новый класс физических законов, получивших название законов квантовой механики[60], поскольку они имеют дело с поведением («механикой») частиц среды («квантов»). Появившись всего два года назад, новые законы квантовой механики, тем не менее, уже успешно проявили себя в объяснении поведения атомов и молекул.

Чандрасекар читал в книге Зоммерфельда о первой, предварительной версии этих законов. Однако, как объяснил Зоммерфельд, эти предварительные законы оказались неудовлетворительными. Они хотя и находились в согласии с экспериментами над простыми атомами и молекулами, такими как водород, не могли рассчитать поведение более сложных. Кроме того, эти законы не были логически связаны друг с другом и другими физическими законами. Они были не более чем набором неэстетичных эмпирических правил вычисления.

Новый вариант законов, хотя и более радикальный по форме, выглядел гораздо более многообещающим. Он объяснял сложные атомы и молекулы и, казалось, хорошо согласовывался с остальной физикой.

Чандрасекар потрясенно слушал, боясь пропустить хоть слово.

Квантовая механика и строение белых карликов

Перед расставанием Зоммерфельд подарил Чандрасекару оттиски своей только что написанной статьи. Она содержала основы законов квантовой механики, которые управляют большим числом электронов, заключенных в малом объеме, например в металле.

Чандрасекар как зачарованный прочел оттиски, разобрался в них, а затем много дней провел в университетской библиотеке, изучая все научные статьи по этой теме, которые только смог разыскать. Особенно интересной оказалась статья, озаглавленная «О конденсированном веществе», английского физика Р.Х. Фоулера, опубликованная 10 декабря 1926 г. в журнале Monthly Notices of the Royal Astronomical Society (Ежемесячные записки Королевского астрономического общества). Статья Фоулера указала Чандрасекару на замечательную книгу «Внутреннее строение звезд» знаменитого британского астрофизика Артура С. Эддингтона, в которой Чандрасекар наткнулся на описание загадки белых карликов.

Белые карлики — это определенный тип звезд, обнаруженный астрономами с помощью телескопов. Загадочной в них была чрезвычайно высокая плотность вещества, находящегося внутри этих звезд, гораздо большая, чем та, с которой до сих пор сталкивался человек. Открывая книгу Эддингтона, Чандрасекар, конечно, не знал, что берясь за раскрытие загадки столь высокой плотности, он и Эддингтон в конце концов с неизбежностью столкнутся с возможностью того, что массивные звезды, погибая, могут схлопнуться, превратившись в черные дыры.

«Вероятно, белых карликов очень много», — прочитал Чандрасекар в книге Эддингтона. «Достоверно известны только три, но все они расположены на малом расстоянии от Солнца… Самая известная из этих звезд — спутник [обычной звезды] Сириуса», который называют Сириус В. Сириус и Сириус В — шестая и седьмая ближайшие к Земле звезды, расстояние до них составляет 8,6 св. лет. Сириус, кроме того, — самая яркая звезда на небе. Сириус В обращается вокруг Сириуса так же, как Земля вокруг Солнца, но Сириусу В требуется 50 лет, чтобы закончить один оборот, тогда как Земле — только год.

Эддингтон описал, как астрономы на основе наблюдений в телескоп оценили массу и диаметр Сириуса В. Масса составила 0,85 солнечной, а диаметр 118 000 км. Это означало, что средняя плотность Сириуса В равнялась 61000 г/см³, т. е. в 61 000 раз больше плотности воды, или примерно 1 тонна в кубическом дюйме! «И хотя этот аргумент был известен уже некоторое время», — писал Эддингтон, обычно считалось необходимым добавлять в заключение “это абсурдно”». Большинство астрономов не могло всерьез воспринимать плотность, столь значительно превышающую ту, которая когда-либо встречалась на Земле. Но если бы они узнали всю истину, обнаруженную в результате более поздних астрономических наблюдений (масса 1,05 солнечной, диаметр 31 000 км и плотность 4 млн г/см³ или 60 т/дюйм³), они сочли бы это еще более абсурдным (рис. 4.1).

Далее Эддингтон описал новый ключевой подход, подкрепляющий «абсурдное» положение, согласно которому Сириус В в 61 тыс. раз плотнее воды: если Сириус В действительно столь плотный, то, в соответствии с законами гравитации Эйнштейна, свет, проходя сквозь его мощное гравитационное поле, «покраснел» бы на 6/100 000 — сдвиг, в 30 раз более сильный, чем для света, излучаемого Солнцем, и потому легко обнаружимый. Кажется это предсказание красного смещения было проверено как раз перед тем, как книга Эддингтона была направлена в печать в 1925 г., астрономом В.С. Адамсом в обсерватории Маунт Вильсон, расположенной на вершине горы близ Пасадены в Калифорнии[61].

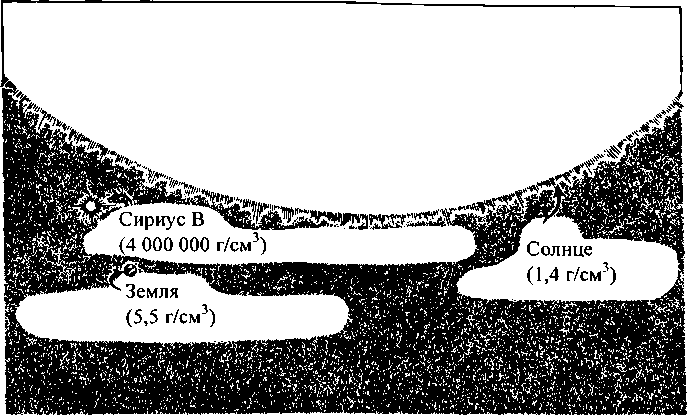
4.1. Сравнение размеров и средних плотностей Солнца, Земли и белого карлика Сириус В на основе современных данных

«Профессор Адамс убил сразу двух зайцев, — писал Эддингтон, — он выполнил еще одну проверку общей теории относительности Эйнштейна и подтвердил наши подозрения относительно того, что вещество с плотностью, в 2000 раз большей, чем у платины, не только возможно, но и реально существует во Вселенной». Еще дальше в книге Эддингтона Чандрасекар нашел описание того, как внутренняя структура звезд, таких как Солнце или Сириус В, поддерживается посредством баланса между внутренним давлением и гравитационным сжатием. Природа подобного баланса может быть понята (у Эддингтона этого нет) из аналогии со сжимаемым в руках мячиком (левая часть рис. 4.2). Внешняя сила сжатия ваших рук в точности компенсируется направленной наружу силой давления воздуха в мячике — давления, которое создается молекулами воздуха, бомбардирующими резиновую стенку мяча.

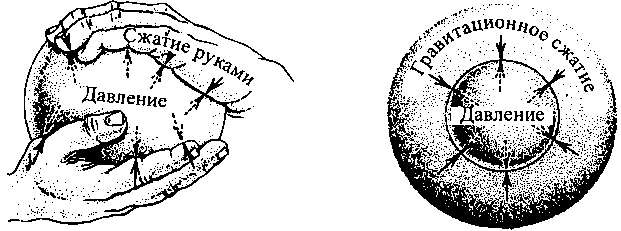
4.2. Баланс между силой давления ваших рук и давлением внутри мяча (слева) и аналогичный баланс между гравитационным сжатием (весом) внешней оболочки звездного вещества и давлением внутреннего объема звезды (справа).

Для звезды (правая часть рис. 4.2) аналогом ваших рук является вес внешней оболочки звездного вещества, а аналогом воздуха в мяче — вещество внутри оболочки. Граница между внешней оболочкой и внутренним шаром может быть выбрана совершенно произвольно — на глубине одного метра, километра, тысячи километров от поверхности звезды… Где бы ни была выбрана граница, должно выполняться требование: вес внешней оболочки, сжимающий внутреннее ядро (гравитационное сжатие внешней оболочки), в точности скомпенсирован давлением молекул внутреннего шара, сталкивающимися с этой оболочкой. Этот баланс, с необходимостью возникающий в каждом месте внутри звезды, определяет структуру звезды, т. е. детали того, как давление, гравитация и плотность меняются от поверхности звезды вглубь, к ее центру.

В книге Эддингтона также обсуждался не дающий покоя физикам парадокс, связанный с представлениями того времени о структуре белых карликов. Эддингтон полагал (так же как и все астрономы в 1925 г.), что давление вещества белых карликов, так же как и в вашем мяче, должно быть обусловлено его теплом. Тепло заставляет атомы вещества двигаться внутри звезды с высокими скоростями, сталкиваясь друг с другом и бомбардируя поверхность границы между внешней оболочкой звезды и его внутренним ядром. При «макроскопическом» рассмотрении, слишком грубом, чтобы различать отдельные атомы, все, что мы можем измерить, это полную силу ударов атомов, которые сталкиваются, скажем, с одним квадратным сантиметром поверхности. Эта полная сила и есть давление внутри звезды.

Когда звезда охлаждается, испуская излучение во внешнее пространство, ее атомы начинают двигаться медленнее, давление ослабевает, и вес внешней оболочки сжимает внутреннее ядро до меньшего объема. Это сжатие вновь нагревает звезду, увеличивая внутреннее давление, пока не будет достигнут новый баланс сжатие-давление, но уже при меньших размерах, чем прежде. Таким образом, поскольку Сириус В продолжает постепенно охлаждаться, излучая тепло в межзвездное пространство, он должен мало-помалу сокращаться в размерах.

Когда закончится это сжатие? Какова окончательная судьба Сириуса В? Самый очевидный (но неверный) ответ, что звезда будет уменьшаться до тех пор, пока не станет столь малой, что превратится в черную дыру, был неприемлем для Эддингтона. Он отказывался даже рассматривать его. Единственное разумное решение, которое он еще мог представить, состояло в том, что звезда должна в пределе охладиться и затем будет поддерживаться уже не тепловым давлением (т. е. давлением, обусловленным теплом), а другим известным в 1925 г. типом давления, а именно, тем, которое обнаруживается в твердых телах, например, в обычном камне, обусловленным отталкиванием электронов близко расположенных атомов. Но как (неправильно) считал Эддингтон, такое «каменное давление» возможно лишь в том случае, если плотность звезды близка к плотности камня — несколько грамм на кубический сантиметр (в 10 тыс. раз меньше, чем плотность Сириуса В).

Такая последовательность аргументов приводила к парадоксу Эддингтона. Чтобы расшириться до плотности камня и тем самым быть в состоянии удерживать себя после охлаждения, Сириусу В требуется совершить колоссальную работу против сил собственной гравитации, а физики не знали адекватного такой работе источника энергии внутри звезды. «Представьте тело, постоянно теряющее тепло, но тем не менее теряющее его недостаточно, чтобы охладиться», — писал Эддингтон. «Это любопытная проблема, и можно было бы сделать множество причудливых предположений касательно того, что в действительности происходит. Мы же оставим в стороне эту трудность, поскольку она не обязательно является неизбежной».

Чандрасекар нашел разрешение этого парадокса 1925 г. в статье Р.Х.Фоулера 1926 г. «О плотном веществе». Решение заключалось в недостаточности законов физики, использованных Эддингтоном. Эти законы необходимо было заменить новыми законами квантовой теории, которые описывали давление внутри Сириуса В и других белых карликов не как обусловленное теплом, а как новый, квантовомеханический феномен: вырожденное движение электронов, также называемое электронным вырождением[62].

Вырождение электронов напоминает человеческую клаустрофобию. Когда вещество сжато до плотности, в 10 тыс. раз превышающей плотность камня, облако электронов, окружающее каждое атомное ядро, занимает в 10 тыс. раз более тесную ячейку. Поэтому каждый электрон оказывается заключенным в «клетку», имеющую объем, в 10 тыс. раз меньший того, в котором ему раньше позволялось двигаться. Имея в распоряжении столь малый объем, электрон, как человек больной клаустрофобией, начинает непроизвольно метаться. Он носится по своей маленькой клетке с очень высокой скоростью, с большой силой ударяясь об электроны в прилегающих ячейках. Это вырожденное движение, как его называют физики, не может быть остановлено охлаждением вещества. Ничто не может его остановить; законы квантовой механики вынуждают электрон двигаться даже при температуре вещества равной абсолютному нулю.

Это вырожденное движение есть следствие особенности вещества, о которой и не думали ньютоновские физики, особенности, называемой корпускулярно-волновым дуализмом. Каждая частица (корпускула), в соответствии с квантовой механикой, при определенных условиях ведет себя как волна, а волна любого типа, при некоторых специальных условиях, — как частица. Поэтому волны и частицы в действительности являются одной и той же сущностью, которая иногда ведет себя как частица, а иногда — как волна.

* * *

Электронное вырождение проще всего понять в рамках дуализма волна-частица. Когда вещество сжато до высокой плотности, и каждый электрон среды заключен в чрезвычайно малом пространстве, сдавленный электронами соседних ячеек, он начинает вести себя во многом как волна. Длина электронной волны (расстояние между ее гребнями) не может быть больше, чем размер ячейки; если бы она была больше, волна выходила бы за пределы этой ячейки. Далее, частицы, имеющие очень малую длину волны, обязательно будут обладать высокой энергией. (Типичный пример — частица, связанная с электромагнитной волной, — фотон. Фотон рентгеновских лучей имеет гораздо более короткую длину волны, чем у видимого света и, как следствие, фотоны рентгеновских лучей гораздо более энергичны, чем фотоны видимого света. Высокая энергия рентгеновских лучей позволяет им проникать через мягкие ткани и кости человека.)

В случае электронов внутри очень плотного вещества короткая длина волны и, соответственно, высокая энергия приводят к их быстрому движению; это означает, что электрон должен двигаться в своей ячейке как странный сверхбыстрый мутант: наполовину — волна, наполовину — частица. Физики говорят, что электрон «вырожден», и называют давление, вызываемое этим беспорядочным высокоскоростным движением, «давлением вырожденных электронов». Избавиться от этого давления невозможно; оно является неизбежным следствием заключения электрона в малом объеме. Более того, чем больше плотность вещества, тем меньше ячейка, тем меньше длина волны электрона, тем выше его энергия, быстрее движение и, следовательно, больше давление вырождения. В обычном веществе с обычной плотностью давление вырождения настолько мало, что им можно пренебречь, но при огромных плотностях белых карликов оно должно быть чрезвычайно большим.

* * *

Когда Эддингтон писал свою книгу, электронное вырождение еще не было предсказано, и поэтому не было никакой возможности правильно рассчитать, как камень или любой другой материал ответит на сжатие до ультравысоких плотностей Сириуса В. С появлением законов электронного вырождения, подобные вычисления стали возможны, и они действительно были предложены и осуществлены Фоулером в статье 1926 г.

Врезка 4.1

Краткая история корпускулярно-волнового дуализма

Уже во время Исаака Ньютона (конец 1600-х) физики столкнулись с вопросом: состоит ли свет из частиц или волн. Ньютон, хотя и колебался, все же склонялся к частицам и назвал их корпускулами, в то время как Христиан Гюйгенс приводил доводы в пользу волн. Представление о частицах света Ньютона возобладало до начала 1800-х, когда открытие, что свет может сам с собой интерферировать (глава 10), убедило физиков в правильности волновых воззрений Гюйгенса. В середине 1800-х Джеймс Кларк Максвелл поставил волновое описание волны на твердую опору своих объединяющих законов электричества и магнетизма, и физики решили, что проблема, наконец, разрешилась. Однако это было до появления квантовой механики.

В 1890-х Макс Планк заметил в форме спектра излучения, испускаемого очень горячими объектами, намеки на то, что физики что-то упустили в понимании природы света. В 1905 г. Эйнштейн показал то, чего не доставало: свет иногда ведет себя как волна, а иногда как частица (теперь называемая фотоном). Эйнштейн объяснил, что он ведет себя как волна, когда интерферирует сам с собой, но как частица в фотоэлектрическом эффекте, когда слабый пучок света падает на поверхность металла. Луч выбивает электроны из металла по одному, именно так, как если бы с электронами сталкивались, выбивая их с поверхности металла, отдельные частицы света (отдельные фотоны). По энергии выбиваемых электронов Эйнштейн определил, что энергия фотона всегда обратно пропорциональна длине волны света. Таким образом, свойства фотона переплетены с волновыми свойствами: длина волны однозначно связана с энергией фотона. Открытие Эйнштейном дуализма волновых и корпускулярных свойств света и первые квантовомеханические законы физики, которые он начал строить вокруг этого открытия, обеспечили ему в 1922 г. Нобелевскую премию 1921 г.

Хотя Эйнштейн сформулировал общую теорию относительности почти единолично, он был только одним среди многих тех, кто внес свой вклад в законы квантовой механики — законы «царства малого».

Когда Эйнштейн обнаружил дуализм волн/частиц света, он еще не понимал того, что электрон или протон тоже могут вести себя иногда как частицы, а иногда как волны. Об этом никто не догадывался до середины 1920-х, когда Луи де Бройль сформулировал такую гипотезу, а затем Эрвин Шрединдгер использовал ее как основу для полного набора законов квантовой механики, законов, в которых электрон является волной вероятности. Вероятности чего? Вероятности локализации частицы. Эти «новые» законы квантовой механики (которые оказались чрезвычайно успешными в объяснении поведения электронов, протонов, атомов и молекул) не будут нас особенно волновать в этой книге. Однако время от времени некоторые из их особенностей будут все же для нас важны. Такой важной особенностью для этой главы является электронное вырождение.

Из расчетов Фоулера следовало, что поскольку электроны в Сириусе В и других белых карликах сжаты в столь малых ячейках, давление вырождения в них гораздо больше температурного (вызванного теплом). Соответственно, когда Сириус В остывает, его слабое термическое давление исчезает, а огромное давление вырождения остается и продолжает противостоять гравитации.

Таким образом, решение парадокса белых карликов Эддингтона имеет две стороны. Во-первых, Сириус В не сдерживает влияние гравитации с помощью температурного давления, как думали ранее, до появления квантовой механики: основную роль играет давление вырождения. Во-вторых, когда Сириус В остывает, ему нет надобности расширяться до плотности камня, чтобы поддерживать себя; как раз наоборот, он будет вполне удовлетворительно поддерживаться давлением вырождения при существующей плотности 4 млн г/см³.

Читая все это и изучая математические выкладки в Мадрасской библиотеке, Чандрасекар был попросту очарован. Это было его первое соприкосновение с современной астрономией, и он обнаружил глубокие следствия двух, идущих рука об руку, революционных идей физики XX века: общая теория относительности Эйнштейна с новым взглядом на природу пространства и времени проявилась в красноволновом сдвиге света, испускаемого Сириусом В, а новая квантовая механика с корпускулярно-волновым дуализмом была ответственна за внутреннее давление Сириуса В. Такая астрономия представлялась благодатным полем, на котором молодой человек мог бы проявить себя.

Продолжая обучение в Мадрасе, Чандрасекар обнаружил дальнейшие приложения квантовой механики к астрономической Вселенной. Он даже написал небольшую статью о своих идеях, отправил ее в Англию Фоулеру, с которым ранее никогда не встречался, и Фоулер представил ее к публикации.

Наконец, в 1930 г. в возрасте 19 лет Чандрасекар получил индийский эквивалент степени бакалавра и в последнюю неделю июля ступил на борт парохода, отплывающего в далекую Англию. Он был принят для продолжения образования в Кембриджский университет — место, где работали его кумиры Фоулер и Эддингтон.

Предельная масса

Восемнадцать дней плавания по морю из Мадраса в Саутгемптон были для Чандрасекара первой за много месяцев возможностью спокойно подумать о физике, не отвлекаясь на рутину учебы и экзаменов. Морское уединение способствовало размышлениям, которые были весьма плодотворны. Настолько, что фактически помогли получить ему Нобелевскую премию, правда, лишь 54 года спустя и только после серьезной борьбы за признание мировым астрономическим сообществом.

На борту парохода Чандрасекар позволил своим мыслям вернуться к белым карликам, парадоксу Эддингтона и разрешению парадокса Фоулером. Решение Фоулера почти наверняка было правильным, и другого не было. Однако Фоулер до конца не разработал детали баланса между вырожденным давлением и гравитацией в звездах типа белого карлика, не рассчитал также и их внутреннюю структуру: каким образом от поверхности к центру меняются плотность, давление и гравитация звезды. И это был вызов — дразнящая проблема, помогающая к тому же бороться со скукой во время долгого путешествия.

Чтобы найти опору при исследовании структуры звезды, Чандрасекару необходимо было получить ответ на следующий вопрос.

Допустим, вещество, из которого состоит белый карлик, уже сжато до некоторой плотности (например, до 1 млн г/см³). Сожмем вещество (т. е. уменьшим его объем и увеличим плотность) еще на 1 %. Вещество будет противиться этому дополнительному сжатию, увеличивая свое внутреннее давление. На сколько процентов возрастет это давление? Физики используют термин «адиабатический коэффициент» для такого процентного изменения давления, обусловленного одним процентом дополнительного сжатия. В этой книге я буду пользоваться более наглядным названием — сопротивление сжатию, или просто сопротивление. (Его не следует путать с «электрическим сопротивлением», это совершенно разные понятия.)

Чандрасекар вывел сопротивление сжатию, изучая шаг за шагом последствия однопроцентного увеличения плотности вещества белого карлика: результирующее уменьшение размера электронной ячейки, уменьшение длины волны электрона, увеличение его энергии и скорости и, наконец, возрастание давления. Результат оказался прост: однопроцентное увеличение плотности приводит к увеличению давления на 5/3 % (1,667 %). Сопротивление вещества белого карлика, следовательно, было равно 5/3.

За много десятилетий до плавания Чандрасекара астрофизики рассчитали составляющие баланса между гравитацией и давлением внутри любой звезды, сопротивление сжатию которой не зависит от глубины. То есть звезды, давление и плотность которой возрастают так, что если продвигаться все глубже внутрь, увеличение плотности на 1 % будет по-прежнему сопровождаться тем же фиксированным приращением давления. Детали получающейся структуры звезды содержались в книге Эддингтона «Внутреннее строение звезд» — этой книгой Чандрасекар весьма дорожил и потому взял ее с собой на борт корабля. Поэтому когда Чандрасекар обнаружил, что вещество белого карлика имеет не зависящее от давления сопротивление сжатию, он был очень доволен. Теперь, обратившись к книге Эддингтона, он мог сразу узнать внутреннюю структуру звезды: как плотность и давление меняются от поверхности к центру.

Среди прочего открытого Чандрасекаром в результате объединения формул, приведенных в книге Эддингтона, с его собственными вычислениями, были выведены значения плотности и скорости вырожденного движения электронов в центре Сириуса В. Ответ состоял в следующем: плотность в центре звезды составляла 360 тыс. г/см³ (или 6 т/дюйм³); средняя скорость электронов = 57 % скорости света.

Как неудобно много! Чандрасекар, как и Фоулер до него, рассчитывал сопротивление вещества белых карликов, основываясь на законах квантовой механики, но игнорируя релятивистские эффекты. Однако если какой-либо объект движется с околосветовой скоростью (даже если это частица, управляемая квантовомеханическими законами), то становятся важными эффекты теории относительности. При скорости, составляющей 57 % скорости света, эти эффекты не должны быть особенно велики, но у более массивного белого карлика большая гравитация требует большего давления в центре звезды для поддержания баланса сил, и средняя скорость электронов, соответственно, будет больше. В таком белом карлике уже нельзя игнорировать релятивистские эффекты. Поэтому Чандрасекар вернулся к исходной точке своего анализа — вычислению сопротивления вещества белого карлика, чтобы на этот раз постараться учесть релятивистские эффекты.

Но их строгий учет потребовал бы объединения законов специальной теории относительности и законов квантовой механики, объединения, которое было разработано позднее совместными усилиями величайших физических умов. Чандрасекару, только недавно закончившему университет, в одиночку это было, конечно, не под силу. Однако уже тогда он смог достаточно оценить принципиальные эффекты, вызываемые высокой скоростью электронов.

Квантовая механика утверждает, что когда достаточно плотное вещество сжимается еще больше, делая каждую электронную ячейку еще меньше, длина волны электрона должна уменьшаться и, соответственно, должна увеличиваться энергия вырожденного движения. Чандрасекар, однако, понял, что природа дополнительной энергии электронов различна и зависит от того, движется ли электрон много медленнее света или же со скоростью, близкой к световой. Если перемещение электрона медленное, то, как обычно, увеличение энергии означает более быстрое движение, т. е. более высокую скорость. Если же электрон движется уже с околосветовой скоростью, то его скорость не сможет сколько-нибудь значительно увеличиться (иначе она превысит световой предел!). Поэтому приращение энергии принимает другую форму, незнакомую в повседневной жизни: дополнительная энергия переходит в инерционность, т. е. возрастает сопротивление электрона ускорению.

Эти две различные судьбы добавочной энергии (дополнительная скорость против дополнительной инерционности) приводят к разным увеличениям электронного давления, а следовательно, и к разным сопротивлениям сжатию. Чандрасекар установил: при низких скоростях электрона сопротивление равно 5/3, как он и рассчитал раньше, а при высоких — 4/3.

Объединив затем полученное им сопротивление 4/3 для релятивистски вырожденного вещества (т. е. вещества настолько плотного, что вырожденные электроны движутся со скоростями, близкими к скорости света) с формулами, приведенными в книге Эддингтона, Чандрасекар вывел свойства белых карликов с высокой плотностью и большой массой. Результат оказался поразительным: вещество с высокой плотностью с трудом может сдерживать гравитацию — настолько, что действие гравитации может быть уравновешено давлением, только если масса звезды меньше 1,4 солнечной. Это означало, в принципе не может существовать белых карликов с массой, превышающей 1,4 массы Солнца!

Имея достаточно ограниченные знания по астрофизике, Чандрасекар был озадачен полученным странным результатом. Только позже, после обсуждения его с Эддингтоном и другими учеными в Кембридже, он пришел к пониманию. Если белый карлик тяжелее Солнца в 1,4 раза, гравитация полностью превозмогает давление вырождения. Если более тяжелая звезда истощает свой внутренний запас тепла и остывает, тяготение выигрывает противоборство с давлением и заставляет звезду неминуемо сжиматься. Но до каких пор? Ответ (в нейтронную звезду или черную дыру) мы рассмотрим в следующих двух главах. Однако в то время Чандрасекар был еще далек от таких проблем.

В тот момент он был просто поставлен в тупик. Вновь и вновь он проверял свои вычисления, но не находил ошибки. Поэтому в оставшиеся несколько дней своего путешествия он старательно записал результаты, оформив их для публикации в две статьи. В одной он описал свои выводы о структуре белых карликов малой массы и плотности, таких как Сириус В. В другой очень кратко объяснялся его вывод, согласно которому не существует белых карликов в 1,4 раза тяжелее Солнца.

* * *

Когда Чандрасекар прибыл в Кембридж, Фоулер был в отъезде. В сентябре, после возвращения Фоулера, Чандрасекар сразу же посетил его и вручил обе свои статьи. Фоулер одобрил первую и отослал ее для публикации в Philosophical Magazine, вторая же статья о максимальной массе белых карликов привела его в недоумение. Он не смог понять доказательства невозможности существования белых карликов с массой, большей 1,4 солнечной массы, полученное Чандрасекаром, но поскольку он был скорее физик, чем астроном, то попросил своего коллегу, известного астронома Е.А. Милна посмотреть статью. Когда и тот не смог понять приводимых в ней доказательств, Фоулер отказался рекомендовать статью в печать.

Чандрасекар был раздосадован. Прошло уже три месяца, как он приехал в Англию, и два месяца Фоулер держал его рукописи. Слишком долго, чтобы ждать одобрения для публикации. Уязвленный Чандрасекар прекратил все попытки опубликовать вторую статью в Британии и отослал по почте рукопись в Америку, в Astrophysical Magazine.

Несколько недель спустя пришел ответ редактора из Чикагского университета: рукопись послана на рецензию американскому физику Карлу Эккарту. В рукописи Чандрасекар приводил без объяснения результаты своих релятивистских и квантовомеханических расчетов, согласно которым сопротивление сжатию при высокой плотности среды составляет 4/3. Это сопротивление, равное 4/3, было существенно для установления предела массы белого карлика. Если бы сопротивление было больше, белые карлики могли бы быть сколь угодно тяжелыми, и Эккарт думал, что оно действительно больше. Чандрасекар немедленно дал ответ, содержащий математическое доказательство равенства сопротивления 4/3 (четырем третям). Эккарт, вникнув в детали, признал правоту Чандрасекара и одобрил рукопись для публикации. Наконец, спустя год после написания она была напечатана[63].

Реакцией астрономического сообщества было непроницаемое молчание. Казалось, никто не заинтересовался. Поэтому Чандрасекар, желая поскорее получить степень доктора философии, обратился к более насущным задачам.

Три года спустя, получив степень доктора, Чандрасекар посетил Россию, чтобы обменяться идеями с советскими учеными. В Ленинграде молодой армянский астроном Виктор Амазаспович Амбарцумян заявил Чандрасекару, что ни один астроном в мире не поверит в его странный предел массы до тех пор, пока на основании физических законов он не рассчитает массы достаточного числа белых карликов и ясно не покажет, что все они лежат ниже провозглашенного порога. При этом было бы явно недостаточно, утверждал Амбарцумян, чтобы Чандрасекар проанализировал только белые карлики с относительно низкой плотностью и сопротивлением, равным 5/3, и белые карлики с чрезвычайно высокой плотностью и сопротивлением 4/3. Ему следовало бы также исследовать несколько белых карликов с промежуточными значениями плотности и сопротивления и показать, что они также имеют массу, меньшую 1,4 солнечной. По возвращении в Кембридж Чандрасекар принял вызов Амбарцумяна.

В качестве основы для анализа белых карликов с промежуточными значениями плотности необходимо было иметь уравнение состояния их вещества при любых значениях плотности — от низкой до предельно большой. (Под термином «состояние» вещества физики понимают плотность и давление в веществе, или, что то же самое, его плотность и сопротивление сжатию, поскольку из плотности и сопротивления можно вычислить давление. Под «уравнением состояния» понимается соотношение между сопротивлением и плотностью, т. е. сопротивление «как функция» плотности.)

К концу 1934 г., когда Чандрасекар принял вызов Амбарцумяна, уравнение состояния для белых карликов, благодаря вычислениям Эдмунда Стоунера из университета Лидса в Англии и Вильгельма Андерсона из Тартусского университета в Эстонии, было уже известно. Уравнение состояния Стоунера — Андерсона показало, что когда вещество белого карлика сжимается все сильнее и сильнее, переходя от нерелятивистского режима низкой плотности и малых скоростей электронов в релятивистскую область чрезвычайно высоких плотностей и околосветовых скоростей движения электронов, сопротивление вещества сжатию плавно спадает от 5/3 до 4/3 (левая часть рис. 4.3). Трудно придумать более простое поведение.

Чтобы ответить на вызов Амбарцумяна, Чандрасекар должен был соединить уравнение состояния (зависимость сопротивления от плотности) с законами баланса между давлением и гравитацией и, исходя из этого, получить дифференциальное уравнение[64], описывающее внутреннюю структуру звезды, т. е. изменение плотности звезды в зависимости от расстояния до ее центра. Затем требовалось решить полученное дифференциальное уравнение для десятка или около того звезд, плотность вещества в центре которых меняется от низких до чрезвычайно высоких значений. Только решая дифференциальное уравнение для каждой отдельной звезды, он мог узнать ее массу и установить меньше ли она 1,4 солнечной.

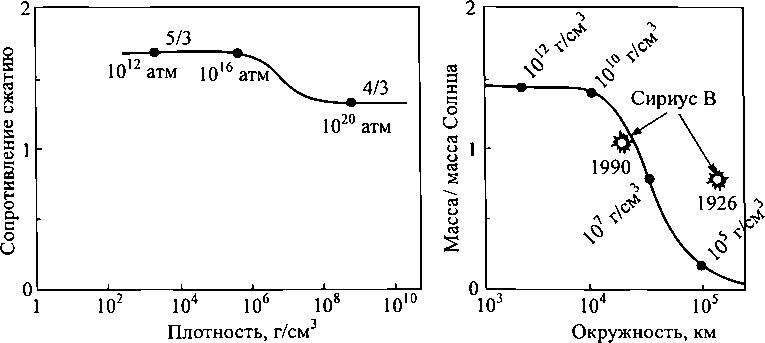
4.3. Уравнение состояния вещества белых карликов, т. е. соотношение между плотностью вещества и сопротивлением сжатию (слева). По горизонтальной оси отложена плотность, до которой сжато вещество, по вертикальной — сопротивление (увеличение давления, в процентах, вызванное ростом плотности на 1 %). Вдоль кривой проставлены значения давления сжатия (равные внутреннему давлению) в единицах атмосферного давления. Диаметр (по горизонтали) и масса (по вертикали) звезд типа белых карликов, рассчитанные Чандрасекаром с помощью механического арифмометра «Брауншвайгер», принадлежавшего Эддингтону (справа)

Для звезд как с малой, так и с предельно большой плотностью, исследованных Чандрасекаром на борту парохода, решение соответствующего дифференциального уравнения и вытекающее из него строение звезды нашлось в книге Эддингтона. Однако для звезд с промежуточными значениями плотности вывести решение с помощью математических формул Чандрасекару никак не удавалось. Вычисления были слишком сложны. Ничего не оставалось, кроме как решить дифференциальные уравнения численно, с помощью счетной машины.

В 1934 г. счетные машины весьма отличались от тех компьютеров, которые появились в 90-е годы. Они напоминали, скорее, простейшие из карманных калькуляторов. За один раз они могли лишь перемножить два числа, причем пользователю требовалось сначала вручную ввести эти числа, а затем повернуть рукоятку. Рукоятка приводила в движение сложную систему шестеренок и колесиков, выполнявших умножение и выдававших ответ.

Но даже и такие калькуляторы были тогда роскошью, и получить к ним доступ было непросто. У Эддингтона, однако, был один — «Брауншвайгер», размер которого примерно соответствовал размеру настольных персональных компьютеров 90-х, и поэтому Чандрасекар, к тому времени уже хорошо знакомый с великим человеком, просто пришел к Эддингтону и попросил на время одолжить ему машину. В тот момент Эддингтон был вовлечен в спор о белых карликах с Милном и был весьма заинтересован поскорее узнать их детально рассчитанную внутреннюю структуру; поэтому он позволил Чандрасекару перенести «Брауншвайгер» в его комнату в Тринити-колледже,

Вычисления были длинными и утомительными. Каждый вечер после обеда Эддингтон, работавший в Тринити-колледже, поднимался к Чандрасекару, чтобы приободрить его и взглянуть, как продвигается дело.

Наконец, много дней спустя, Чандрасекар закончил. Он ответил на вызов Амбарцумяна. Для каждого из десяти типичных белых карликов он рассчитал внутреннюю структуру и затем, зная ее, — полную массу и поперечный размер звезды. Все массы, как и предполагалось, оказались меньше 1,4 солнечной. Более того, когда он нанес все значения масс и диаметров на диаграмму и соединил точки, получилась одна плавная кривая (правая часть рис. 4.3); измеренные массы и поперечники Сириуса В, а также других известных белых карликов относительно хорошо согласовывались с полученной кривой. (С учетом исправлений, полученных в результате современных астрономических наблюдений, согласие становится еще лучше; обратите внимание на новые значения 1990 г. массы и поперечника Сириуса В на рис. 4.3.) Гордый своими результатами, полагая, что астрономы всего мира, наконец, согласятся с его утверждением, что белые карлики не могут быть тяжелее, чем 1,4 массы Солнца, Чандрасекар был счастлив.

Особенно приятной казалась возможность представить полученные результаты на заседании Королевского астрономического общества в Лондоне. Выступление было назначено на пятницу 11 января. Согласно протоколу, детали повестки дня предстоящего заседания должны были оставаться в секрете вплоть до начала заседания, однако мисс Кей Вильямс, ученый секретарь Общества и близкий друг Чандрасекара, обычно тайно заранее посылала ему программу выступлений. Получив в четверг вечером программу по почте, Чандрасекар был удивлен, обнаружив, что сразу после его доклада следует выступление Эддингтона по вопросу о «релятивистском вырождении». Чандрасекар недоумевал. В течение последних нескольких месяцев Эддингтон заходил навестить его, по крайней мере, раз в неделю, читал черновики, но ни разу не упомянул о собственных исследованиях на ту же тему!

Подавив досаду, Чандрасекар спустился к обеду. Эддингтон был в столовой, обедая за главным столом. Приличия, однако, не позволяли просто так побеспокоить столь известного человека, даже если вы были с ним знакомы, и он проявлял некий интерес к вашей деятельности. Поэтому Чандрасекар, сдержавшись, просто сел в стороне.

Врезка 4.2

Объяснение масс и окружностей звезд — белых карликов

Для качественного понимания того, почему белые карлики имеют такие массы и окружности, которые показаны на рис. 4.3, посмотрите на иллюстрацию внизу. На ней показаны среднее давление и гравитация в белом карлике (отложены по вертикали) как функция окружности звезды (отложены вправо) или плотности (отложена влево). Если Вы сжимаете звезду, так что увеличивается ее плотность и уменьшается окружность (движение на рисунке влево), то давление звезды повышается в соответствии со сплошной кривой, быстрее для плотностей, где сопротивление сжатию равно 5/3, и медленнее для больших плотностей, когда сопротивление — 4/3. Это же самое сжатие звезды заставляет поверхность звезды приближаться к ее центру, таким образом, увеличивая силу внутренней гравитации звезды в соответствии с ходом штриховых линий. Скорость увеличения гравитации аналогична 4/3 у сопротивления: увеличение гравитации на 4/3 на каждый процент сжатия. На рисунке показаны несколько штриховых линий гравитации для нескольких значений массы, и чем больше масса звезды, тем сильнее ее гравитация.

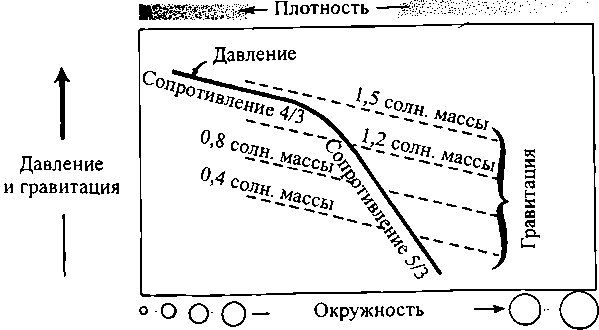
В каждой звезде, например в звезде с массой в 1,2 солнечной, гравитация и давление должны уравновешивать друг друга. Поэтому звезда должна существовать на пересечении штриховой линии гравитации, отмеченной как «1,2 солнечной массы», и сплошной кривой давления: это пересечение определяет окружность звезды (указана на горизонтальной оси графика). Если окружность будет больше, то штриховая линия гравитации звезды будет проходить выше сплошной кривой давления, гравитация преодолеет давление, и звезда будет схлопываться. Если окружность меньше, то давление преодолевает гравитацию, и звезда взрывается.

Пересечения нескольких штриховых линий со сплошной кривой соответствуют массам и окружностям равновесия белых карликов, показанным в правой части рис. 4.3. Для звезды меньшей массы (самая нижняя штриховая линия) окружность в точке пересечении является большой. Для звезды с большей массой (более высокая штриховая линия) — окружность меньше. Для звезды с массой больше 1,4 солнечной вообще нет пересечений, штриховая линия гравитации лежит всегда выше сплошной кривой давления и, таким образом, гравитация всегда преодолевает давление, независимо от того, какова окружность звезды, и заставляет звезду схлопываться.

После обеда Эддингтон сам отыскал Чандрасекара и сказал: «Я попросил Смарта дать Вам полчаса вместо обычных пятнадцати минут». Чандрасекар поблагодарил и собрался было что-то спросить относительно выступления Эддингтона, но тот, извинившись, откланялся. Раздражение Чандрасекара переросло в смятение.

Схватка

На следующее утро Чандрасекар на поезде приехал в Лондон и взял такси до Берлингтон Хаус, где размещалось Королевское астрономическое общество. Когда он со своим другом Биллом Мак-Крэем ожидал начала заседания, к ним приблизился проходивший мимо Эддингтон, и Мак-Крэй, только что ознакомившийся с программой, спросил: «Профессор Эддингтон, что Вы нам поведаете о релятивистском вырождении?» В ответ Эддингтон, повернувшись к Чандрасекару, сказал: «Это будет для вас сюрпризом» и удалился, оставив Чандрасекара в еще большем недоумении.

Но вот заседание началось. Время медленно тянулось, пока президент Общества делал разные объявления, а астрономы выступали с докладами. Наконец, подошла очередь Чандрасекара. Подавив беспокойство, он выступил безупречно, особенно выделив в своем сообщении полученный им максимальный предел массы белых карликов.

После вежливых аплодисментов членов Общества президент предоставил слово сэру Артуру Эддингтону.

Слева: Артур Стэнли Эддингтон, 1932 г. Справа: Субраманьян Чандрасекар, 1934 г. [Слева: предоставлено UPI/Bettmann; справа: предоставлено С. Чандрасекаром]

Эддингтон начал спокойно, сделав обзор истории исследования белых карликов. Затем, набирая обороты, он описал беспокоящие его следствия существования предельной массы. На диаграмме Чандрасекара, на которой по вертикали отложена масса звезды, а по горизонтали диаметр (рис. 4.4), существовала только одна совокупность масс и диаметров звезд, для которой гравитация может быть уравновешена нетепловым давлением (т. е. давлением, которое остается после остывания звезды) — это и есть белые карлики. В области слева от кривой белых карликов Чандрасекара (заштрихованная область, звезды с меньшим диаметром) давление вырождения полностью пересиливает гравитацию, что должно для любой звезды, находящейся в заштрихованной области, привести к взрыву. Справа от кривой (светлая область, звезды с большим, чем у белых карликов, радиусом), напротив, гравитация превозмогает давление вырождения звезды. Каждая холодная звезда, оказавшаяся в этой области, немедленно схлопнется под действием гравитационного сжатия.

Солнце может существовать в светлой области, поскольку сейчас оно очень горячее; его термическому (обусловленному теплом) давлению удается уравновешивать гравитацию. Однако когда Солнце, в конце концов, остынет, его тепловое давление исчезнет, и Солнце не сможет больше себя поддерживать. Гравитация заставит его сжиматься до все меньших размеров, стискивая электроны Солнца во все уменьшающихся ячейках, пока, наконец, они не смогут противопоставить сжатию достаточное давление вырождения. В процессе такого сжатия — «смерти» масса Солнца будет оставаться почти постоянной, тогда как его диаметр будет уменьшаться и, следовательно, оно будет двигаться влево вдоль горизонтальной линии на рис. 4.4, пока, наконец, не остановится на кривой белых карликов — своей гробнице. В этом состоянии, в виде белого карлика, Солнце будет существовать всегда, постепенно остывая и превращаясь в черный карлик — холодный темный твердый объект, с размером, примерно равным размеру Земли, но в миллионы раз более тяжелый и плотный.

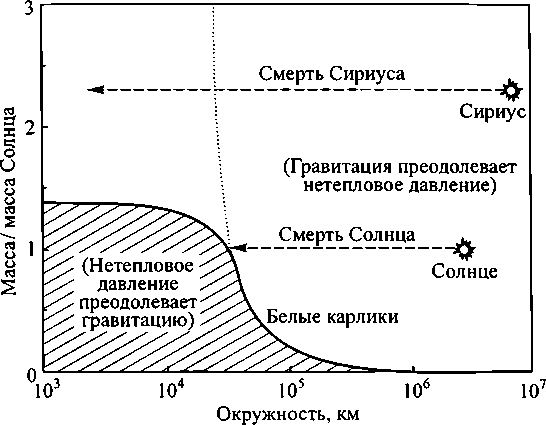
4.4. Когда обычная звезда вроде Сириуса (но не Сириуса В) или Солнца начинает остывать, она должна сжиматься, двигаясь влево на этой диаграмме масс и диаметров звезд. Сжатие Солнца остановится, как только оно достигнет края заштрихованной области (кривая белых карликов). В этом месте давление вырождения сравняется с силами гравитационного сжатия. Сжатие Сириуса, напротив, не может быть остановлено таким же образом, поскольку он никогда не достигнет границы заштрихованной области. Если бы (как заявлял Эддингтон) сопротивление сжатию вещества белых карликов всегда было равно 5/3, т. е. релятивистские эффекты не уменьшали бы его до 4/3 при высоких плотностях, то график зависимости массы от диаметра имел бы вид пунктирной кривой, и сжатие Сириуса остановилось бы на этой линии

Такая конечная судьба Солнца казалась Эддингтону вполне удовлетворительной. Но не конечная судьба звезд, имеющих массу, большую предельной массы, полученной Чандрасекаром (1,4 солнечной), например Сириуса, спутника Сириуса В, массой в 2,3 солнечной. Если Чандрасекар был прав, такая звезда никогда не сможет умереть спокойной смертью, подобной той, что ожидает Солнце. Когда излучение, постоянно испускаемое звездой в пространство, унесет достаточно тепла, и звезда начала остывать, тепловое давление понизится, и гравитационное силы будут уменьшать и уменьшать ее размеры. Но для такой тяжелой звезды, как Сириус, сжатие не может быть остановлено вырожденным давлением. Это становится понятным из рис. 4.4, на котором заштрихованная область не поднимается достаточно высоко, чтобы помешать предначертанному пути сжатия Сириуса. Эддингтон находил это предсказание неприемлемым.