Глава 45 ПРИМЕРЫ ИЗ ТЕРМОДИНАМИКИ

Глава 45

ПРИМЕРЫ ИЗ ТЕРМОДИНАМИКИ

§ 1. Внутренняя энергия

§ 2. Применения

§ 3. Уравнение Клаузиуса –Клайперона

§ 1. Внутренняя энергия

Когда приходится использовать термоди­намику для дела, то оказывается, что она очень трудный и сложный предмет. В этой книге, однако, мы не будем залезать в самые дебри. Эта область особенно интересна для химиков и инженеров, и тем, кому захочется получше познакомиться с ней, следует обратиться к физи­ческой химии или инженерной термодинамике. Есть еще ряд хороших справочных книг, в кото­рых эта тема обсуждается более подробно.

Термодинамика сложна потому, что каждое явление она позволяет описывать многими способами. Если нам нужно описать поведение газа, то мы можем исходить из того, что его давление зависит от температуры и объема, а можно предположить, что объем зависит от давления и температуры. То же самое и с внутренней энергией U: можно сказать, что она определяется температурой и объемом, стоит только выбрать именно эти переменные, но можно говорить о зависимости от температуры и давления или от давления и объема и т. д. В предыдущей главе мы познакомились с дру­гой функцией температуры и объема, называе­мой энтропией S. И теперь ничто не помешает нам построить другие функции этих переменных. Например, функция U-TS тоже зависит от температуры и объема. Таким образом, нам при­ходится иметь дело с большим количеством разных величин, зависящих от разнообразных комбинаций переменных.

Чтобы упростить понимание этой главы, договоримся с самого начала выбрать в качестве независимых переменных температуру и объ­ем. Химики используют для этого температуру и давление, потому что их легче измерять и контролиро­вать в химических реакциях. Но мы используем повсюду в этой главе температуру и объем и изменим этому только в одном месте, чтобы посмотреть, как совершается переход к химическим переменным.

Итак, сначала рассмотрим только одну систему независимых переменных — температуру и объем. Затем нас будут интере­совать только две функции этих переменных: внутренняя энер­гия и давление. Все другие термодинамические функции можно получить с помощью этих двух, но не обязательно это делать именно сейчас. Даже после таких ограничений термодинамика останется еще трудным предметом, но все же уже не столь невоз­можным для понимания!

Сначала немного займемся математикой. Если величина есть функция от двух переменных, то дифференцировать ее придется осторожнее, чем мы это делали раньше, имея дело с одной пере­менной. Что мы понимаем под производной давления по темпе­ратуре? Изменение давления, сопровождающее изменение тем­пературы, разумеется, зависит от того, что случилось с объемом, пока менялась температура. Прежде чем понятие производной по температуре обретет ясный смысл, надо сказать что-то опре­деленное об изменении объема. Например, можно спросить, какова скорость изменения Р относительно Т при постоянном объеме. Тогда отношение изменений обеих этих величин, по существу, обычная производная, которой привыкли присваи­вать символ dP/dT. Мы обычно используем особый символ дР/дТ, он напоминает нам, что Р зависит, кроме Т, еще и от переменной V, и эта переменная не изменяется. Чтобы подчерк­нуть тот факт, что V не изменяется, мы не только используем символ д, но еще пометим индексом остающуюся постоянной переменную (дР/дТ)_у. Конечно, поскольку имеются только две независимые переменные, то это обозначение излишне, но оно, быть может, поможет нам легче пройти сквозь термодинамиче­ские дебри частных производных.

Предположим, что функция f(x, у) зависит от двух незави­симых переменных х и у. Под символом (дf/дх)_умы понимаем самую обычную производную, получаемую общепринятым спо­собом, если у постоянна:

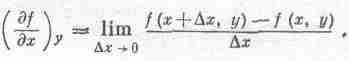
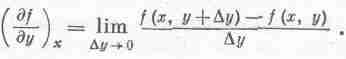
Аналогично определяется и

Например, если f(x, у)=х²+ух, то (df/dx)_y=2x+y, а (дfду)_х=х. Мы можем распространить это на старшие производные:

д²f/дy²или д²f/дудх.

Последний случай означает, что сначала f продифференцировано по х, считая у постоянным, а затем ре­зультат продифференцирован по у, но теперь постоянным стало х. Порядок дифференцирования не имеет значения:

д²fldxdy=д²f/дyдx.

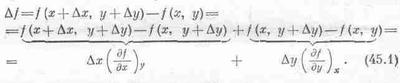
Нам придется подсчитывать изменение Df, происходящее с f(x, у), если х переходит в х+Dх, а у переходит в y+Dy. Будем предполагать, что Dx и Dy бесконечно малы:

Последнее уравнение и есть основное соотношение, связываю­щее приращение Df с Dx и Dy.

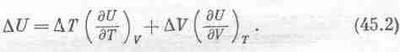
Посмотрим, как используется это соотношение; для этого вычислим изменение внутренней энергии U(Т,V), если тем­пература Т переходит в Т+DT, а объем V переходит в V+DV. Используем формулу (45.1) и запишем

В предыдущей главе мы нашли другое выражение для изме­нения внутренней энергии DU; тогда к подводимому газу прибавлялось тепло DQ:

DU==DQ-РDV. (45.3)

Сравнив (45.2) и (45.3), можно было бы подумать, что P=(дU/дV)_T, но это не так. Чтобы получить верный результат, сначала предположим, что газ получает тепло DQ, причем объем его не изменяется, так что DV=0. Если DV=0, то уравнение (45.3) говорит нам, что DU=DQ, а уравнение (45.2) утверждает, что DU=(дU/дT)_VDT, поэтому (дU/дT)_v=DQ/DT. Отношение DQ/DT—количество тепла, которое нужно подвести к телу, чтобы изменить его температуру на один градус, удерживая объем по­стоянным,— называется удельной теплоемкостью при посто­янном объеме и обозначается символом C_V, Таким образом, мы

показали, что

Теперь снова подведем к газу тепло DQ, но на этот раз догово­римся, что температура газа останется постоянной, а объему мы позволим измениться на DV. В этом случае анализ сложнее, но мы можем вычислить DU, используя аргументы Карно, для чего нам придется снова призвать на помощь цикл Карно из предыдущей главы.

Диаграмма давление — объем для цикла Карно изображена на фиг. 45.1. Мы уже показали, что полная работа, совершаемая газом при обратимом цикле, равна DQ(DT/T), где DQ — тепло, подводимое к газу при температуре Т во время изотермического расширения от V до V+DV, а Т—DТ — это конечная темпе­ратура, которой достигает газ при адиабатическом расширении на втором этапе цикла. Сейчас мы покажем, что эта работа равна, кроме того, заштрихованной площади на фиг. 45.1. Работа газа

во всех случаях жизни равна ?PdV; она положительна, если

газ расширяется, и отрицательна, когда он сжимается. Если вычертить зависимость Р от V, то изменения Р и V изобразятся кривой, в каждой точке которой определенному значению Р соответствует определенное значение V. Работа, произведенная газом, пока его объем изменяется от одного значения до другого

(интеграл ?PdV),— это площадь под кривой, соединяющей на­чальное и конечное значения V. Применим эту идею к циклу Карно и убедимся, что если обойти цикл, помня о знаке совер­шенной газом работы, то чистая работа газа будет равна заштри­хованной на фиг. 45.1 площади.

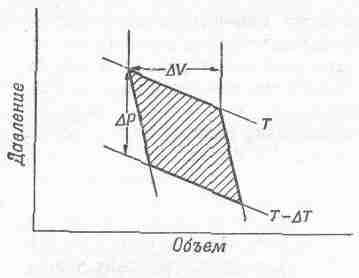
Фиг. 45.1. Диаграмма Р — V для цикла Карно.

Кривые, помеченные Т и Т—DТ,— изотермы; крутые кривые между ни­ми — адиабаты. Когда газ изотермиче­ски расширяется при температуре Т, он получает тепло DQ и увеличивает свой объем на DV; DР—изменение давле­ния при постоянном объеме, темпера­тура в это время падает с Т до Т—DT.

А теперь вычислим эту площадь чисто геометрически. Цикл, который был использован для получения фиг. 45.1, отличается от цикла, описанного в предыдущей главе тем, что теперь DQ и DT бесконечно малы. Наши адиабаты и изотермы очень близки друг к другу, поэтому фигура, описанная жирными линиями на фиг. 45.1, приближается к параллелограмму, когда прира­щения DQ и DТ стремятся к нулю. Площадь этого параллело­грамма в точности равна DVDP (где DV — изменение объема, когда к газу подводится энергия DQ при постоянной темпера­туре, а DР — изменение давления при изменении температуры на DT и постоянном объеме). Легко показать, что заштрихован­ная площадь на фиг. 45.1 равна площади, ограниченной пунк­тиром на фиг. 45.2. А эту фигуру легко превратить в прямо­угольник со сторонами DР и DV, для чего нужно лишь вырезать из нее треугольники и сложить их немного иначе.

Соберем все наши выводы вместе.

Выражение (45.5) содержит в себе суть результатов, следую­щих из аргументов Карно. Всю термодинамику можно вывести из (45.5) и первого закона, содержащегося в уравнении (45.3). Выражение (45.5)— это, в сущности, второй закон, хотя впер­вые Карно сформулировал его несколько иначе, поскольку не пользовался нашим определением температуры.

А теперь можно приступить к вычислению (дUlдV)_T. На­сколько изменится внутренняя энергия U, если объем изменится на DV? Во-первых, внутренняя энергия U меняется за счет подводимого тепла и, во-вторых, за счет совершаемой работы. Подводимое тепло, согласно (45.5), равно

DQ=(dP/дT)_VDV,

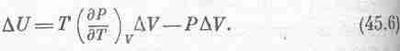
а совершаемая над веществом работа равна —PDV. Поэтому изменение DU складывается из двух кусков

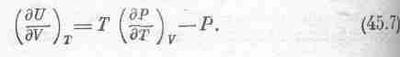
Поделив обе стороны на DV, мы найдем скорость изменения U относительно V при постоянной Т

В нашей термодинамике, где есть только две переменные, Т и V, и только две функции, Р и U, уравнения (45.3) и (45.7) — это основные уравнения, из которых можно вывести все последующие результаты.

§ 2. Применения

Теперь обсудим смысл уравнения (45.7) и посмотрим, почему оно дает ответ на поставленные в предыдущей главе вопросы. Мы занимались рассмотрением такой задачи: в кинетической теории ясно, что рост температуры приводит к увеличению давления, потому что усиливается бомбардировка поршня атомами. Те же физические причины приводят к тому, что при выталкивании поршня от газа отбирается тепло, и чтобы удержать температуру постоянной, надо позаботиться о подводе тепла. При расшире­нии газ остывает, а при нагревании его давление возрастает. Между этими явлениями должна существовать какая-то связь, и она полностью определяется уравнением (45.7). Если мы удерживаем объем постоянным и поднимаем температуру, дав­ление растет со скоростью (дР/дТ)_V. Вот мы и нашли эту связь: если увеличить объем и не подвести какого-то количества тепла для поддержания температуры, то газ остынет, а величина (дU/дV)_Tподскажет нам, сколько именно надо подбавить тепла. Уравнение (45.7) выражает фундаментальную связь между этими двумя эффектами. Именно это мы обещали найти, отправ­ляясь на поиски законов термодинамики. Не зная внутреннего строения газа и лишь веря, что построить вечный двигатель вто­рого рода выше наших сил, мы смогли вывести соотношение между количеством тепла, необходимого для поддержания по­стоянной температуры при расширении газа, и изменением дав­ления газа при нагревании!

Получив от газа все, что нужно, рассмотрим другой случай— резину. Растянув резиновую полоску, мы обнаружили, что ее температура возросла, а нагревание заставило ее сжаться. Какое уравнение дает в случае резины тот же результат, что и уравне­ние (45.3) для газа? Сначала все идет, как и раньше: когда к ре­зине подводится тепло DQ, внутренняя энергия изменяется на DU и производится какая-то работа. Только теперь эта работа равна —FDL вместо PDV, где F — это приложенная к резине сила, a L — длина резиновой полоски. Сила F зависит от тем­пературы и длины резиновой полоски. Заменив в (45.3) PDV на —FDL, получим

DU=DQ+FDL. (45.8)

Сравнивая (45.3) и (45.8), мы убедимся, что уравнение для ре­зины получилось сразу после замены одних букв другими. Если заменить V на L, а Р на —F, то все аргументы цикла Карно ока­жутся применимыми и к резине. Можно тотчас же, скажем, вы­вести, что нужное для растяжения на DL тепло DQ определяется уравнением, аналогичным (45.5): DQ=—Т(дF/дТ)_LDL. Это уравнение говорит нам, насколько увеличится сила, если длина резиновой полоски при нагревании останется постоянной. Надо только узнать, сколько тепла требуется для поддержания по­стоянной температуры при небольшом растяжении полоски. Итак, мы видим, что и к резине, и к газу применимы одни и те же уравнения. Можно даже писать DU=DQ+ADB, где А и В — самые разные величины, сила и длина, давление и объем и т. д. Если интересует поведение газа, нужно заменить A и В на Р и V.

Для примера рассмотрим разность электрических потен­циалов, или электродвижущую силу (э. д. с.) батареи Е, и заряд DZ, прошедший через батарею. Мы знаем, что работа, произво­димая обратимой электрической батареей, например аккуму­лятором, равна EDZ. (Поскольку мы не включили в рассмотре­ние член PDV, то придется потребовать, чтобы объем оставался постоянным.) Посмотрим, что скажет о работе батареи термоди­намика. Если заменить Р на Е, а V на Z, то вместо уравнения (45.6) получится

Это уравнение говорит нам, что при путешествии заряда DZ по батарее меняется внутренняя энергия U. Но почему DU/DZ — это не просто э. д. с. батареи E? Дело в том, что в реальных об­стоятельствах движение зарядов внутри батареи вызывает выделение тепла. Внутренняя анергия батареи изменяется, во-первых, за счет работы, производимой батареей во внешней цепи, и, во-вторых, за счет нагревания батареи. Интересно, что вто­рую часть изменения внутренней энергии опять-таки можно подсчитать, следя, как меняется э. д. с. батареи при изменении температуры. Между прочим, когда заряды текут по батарее, там происходят химические реакции, и уравнение (45.9) указы­вает на отличный способ измерения необходимой для реакции энергии. Для этого нам нужно лишь сделать батарею, работаю­щую на этой реакции, и сначала просто измерить э. д. с., а потом проследить, как меняется э. д. с. с температурой, если ни один заряд не выпускается из батареи!

Мы предположили, что объем батареи можно поддерживать постоянным, только поэтому мы позволили себе пренебречь членом PDV и считать, что работа батареи равна EDZ. Но оказы­вается, что поддерживать объем постоянным технически очень трудно. Гораздо легче держать батарею под постоянным атмо­сферным давлением. Вот почему химики не любят только что написанных нами уравнений: они предпочитают уравнения, которые были бы связаны с постоянным давлением. Мы с самого начала этой главы за независимые переменные приняли V и Т. Химикам больше нравятся Р и Т, поэтому посмотрим теперь, как преобразуются наши выводы при переходе к химической системе переменных. Постарайтесь при этом не ошибиться, потому что мы как-никак сменили детали и перешли от Т и V к Т и Р.

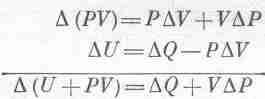
Начнем с (45.3), где DU=DQ-PDV; член PDV можно заме­нить на EDZ или даже на АDВ. Если бы нам удалось как-нибудь заменить PDV на VDP, тогда V и Р поменялись бы ролями и химики остались бы довольны. Тот, кто сообразителен, заметит, что дифференциал произведения PV равен d(PV)=PdV+VdP. Добавив это равенство к (45.3), он получит

Чтобы все наши последующие выводы походили на выводы из уравнения (45.3), давайте будем считать U+PV какой-то новой функцией, назовем ее энтальпией Н, и напишем в таком виде: DH=DQ+VDP.

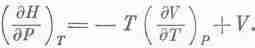
Вот теперь мы готовы перевести все наши рассуждения на химический язык, надо только помнить, что U®H, Р®V, V®P. Химики считают, что вся термодинамика содержится не в уравнении (45.7), а в уравнении

Выяснив, как происходит переход к химическим переменным Т и Р, вернемся к нашим старым переменным. Теперь и уже до конца главы нашими независимыми переменными будут Т и V. Сейчас давайте применим полученные результаты к некото­рым физическим процессам. Сначала рассмотрим идеальный газ. Из кинетической теории известно, что внутренняя энергия газа зависит только от характера движения молекул и от их числа. Внутренняя энергия зависит только от Т, а к V она безразлична. Если изменять V при постоянной Т, то U не изменится. Значит, (dU/dV)_T=0, и уравнение (45.7) говорит нам, что для идеального газа

Т(дP/дT)_V-Р =0^. (45.10)

Уравнение (45.10) — это дифференциальное уравнение, и оно кое-что расскажет нам о Р. Мы расправимся с частной произ­водной так: поскольку частная производная вычислена при постоянном V, можно заменить частную производную обычной, только надо помнить, что все это делается «при постоянном V». Уравнение (45.10) тогда принимает вид

Т=DP/DT-P=0 (при постоянном V), (45.11)

интегрирование не составит для нас труда, и мы получим lnP=lnТ+const (при постоянном V),

P=constXT (при постоянном V). (45.12)

Мы знаем, что давление идеального газа равно

Р=RT/V. (45.13)

Это соотношение совместимо с (45.12), потому что R и V — постоянные. Но зачем же мы мучились, решая эти уравнения? Ведь результат-то был уже известен. Потому что мы пользова­лись двумя независимыми определениями температуры! Однаж­ды мы предположили, что кинетическая энергия молекул про­порциональна температуре. Это предположение привело нас к температурной шкале, которую мы назвали шкалой идеаль­ного газа. Температура Т в уравнении (45.13) отсчитывается по газовой шкале. Мы называли отсчитанную по газовой шкале температуру кинетической температурой. Потом мы определили температуру иначе, и это определение вообще не нуждалось ни в каком веществе. Исходя из второго закона, мы определили то, что можно назвать «абсолютной термодинамической темпера­турой» Т; она появляется в уравнении (45.12). Здесь мы только доказали, что давление идеального газа (идеальный газ для нас нечто, чья внутренняя энергия не зависит от объема) пропор­ционально абсолютной термодинамической температуре. Мы, кроме того, знаем, что давление пропорционально температуре, измеренной по газовой шкале. Таким образом, можно заклю­чить, что кинетическая температура пропорциональна «абсо­лютной термодинамической температуре». Это, конечно, озна­чает, что если бы мы были благоразумны, то показания обеих шкал могли бы всегда жить в согласии. В конце концов эти шкалы можно выбрать так, что они совпадут; постоянную про­порциональности можно положить равной единице. Очень долго люди сами себе создавали трудности, но наконец прев­ратили две шкалы в одну!

§ 3. Уравнение Клаузиуса— Клайперона

Испарение жидкости — это еще одна область, в которой можно применить наши результаты. Предположим, что мы вдвигаем поршень в цилиндр с каким-то веществом.

Естественно задать себе вопрос: как зависит давление от объе­ма, если температура остается постоянной? Иначе говоря, мы хотим начертить изотермические линии на диаграмме Р—V. Вещество в цилиндре — это далеко не идеальный газ, с которым мы имели дело; теперь это жидкость или пар, а может быть, и то и другое вместе. Если сжать вещество достаточно сильно, то оно начнет превращаться в жидкость. Если мы будем увеличи­вать давление, объем изменится очень мало, а наши изотермы при уменьшении объема пойдут резко вверх, как это показано в левой части фиг. 45.3.

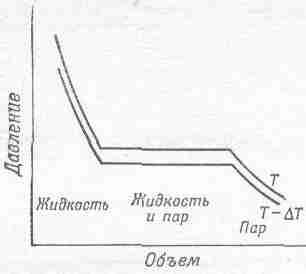
Фиг. 45.3. Изотермы конденси­рующегося пара.

Пар сжимается в цилиндре. Слева — все вещество превратилось в жидкость; справа — вся жидкость испарилась; в середине — в цилиндре сосуществуют жидкость и пар.

Если увеличивать объем, выдвигая поршень из цилиндра, давление будет падать, пока мы не достигнем точки кипения жидкости и в цилиндре появится пар. Дальнейшее вытягивание поршня приведет к более сильному испарению. Когда цилиндр заполнен частично паром, а частично жидкостью, то между ними устанавливается равновесие — жидкость испаряется, пар кон­денсируется, и скорости этих процессов равны. Если предоста­вить пару больший объем, то, чтобы удержать прежнее давле­ние, понадобится больше пара. Поэтому, хоть жидкость все испаряется, давление остается прежним. Вдоль плоской части кривой на фиг. 45.3 давление не изменяется, это давление назы­вается давлением пара при температуре Т. Если объем все увеличивается, наступит момент, когда запасы жидкости иссяк­нут. В такой ситуации давление падает при увеличении объема, ведь теперь мы имеем дело с обычным газом; это изображено в правой части диаграммы Р—V. Нижняя кривая на фиг. 45.3— это изотермическая кривая при более низкой температуре Т—DT. Давление жидкости в этом случае немного меньше, потому что с ростом температуры жидкости расширяются (не все жидкости, вода около точки замерзания поступает наоборот), а давление пара при уменьшении температуры, конечно, падает.

Из двух изотерм можно снова построить цикл, соединив концы их плоских участков (скажем, адиабатами), как это показано на фиг. 45.4. Небольшая зазубрина в нижнем правом углу фигуры несущественна, и мы просто забудем о ней. Исполь­зуем аргументы Карно, которые показывают, как связано тепло, подведенное к жидкости для превращения ее в пар, с работой, совершаемой веществом при обходе цикла. Пусть L—это тепло, необходимое для испарения жидкости в цилиндре. Вспом­ним, как мы рассуждали при выводе уравнения (45.5), и не­медленно скажем, что L(DT/T) равно работе, совершенной ве­ществом. Как и раньше, работа вещества равна площади, за­ключенной внутри цикла. Эта площадь приблизительно равна DP(V_G—V_L), где DР — разность давлений пара при температурах Т и Т—DT, V_G — объем газа, a V_L—объем жидкости. Оба объе­ма надо измерять при давлении, равном давлению пара.

Сравнивая два выражения для работы, мы получаем L(DT/T)= DP(V_G-V_L), или

Уравнение (45.14) связывает скорость изменения давления пара с температурой и количеством тепла, необходимым для испа­рения жидкости. Хотя вывел его Карно, называется оно урав­нением Клаузиуса — Клайперона.

Сравним уравнение (45.14) с результатом, следующим из ки­нетической теории. Обычно V_G гораздо больше V_L. Поэтому V_G-V_L»V_G=RT/P на моль. Если еще предположить, что L — не зависящая от температуры постоянная (хотя это не очень хорошее приближение), то мы получим dP/8T=L/(RT²P). Вот решение этого дифференциального уравнения:

P=const·e^-L/RT. (45.15)

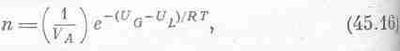
Надо выяснить, в каких отношениях находится это выраже­ние с полученной ранее с помощью кинетической теории за­висимостью давления от температуры. Кинетическая теория говорит, хотя и очень неопределенно, что число молекул пара над жидкостью примерно равно

где U_G—U_L— разность отнесенных к молю внутренних энергий газа и жидкости. Термодинамическое уравнение (45.15) и кине­тическое уравнение (45.16) очень похожи, потому что давление равно nkT, но все-таки это разные уравнения. Однако их можно сделать одинаковыми, если заменить старое предположение L=const предположением о том, что L—U_G=const. Если предположить, что L—U_G — не зависящая от температуры постоянная, то соображения, из которых ранее следовало (45.15), при­ведут теперь к уравнению (45.16).

Это сравнение показывает преимущества и недостатки тер­модинамики по сравнению с кинетической теорией. Прежде всего полученное термодинамически уравнение (45.14) — это точное соотношение, а (45.16) — всего-навсего приближение. Ведь нам пришлось предположить, что U приблизительно постоянна и что наша модель верна. Во-вторых, нам, быть мо­жет, никогда не удастся понять до конца, как газ переходит в жидкость, и все-таки уравнение (45.14) правильно, а (45.16)— это только приближение. В-третьих, хотя мы говорили о прев­ращении газа в жидкость, наши аргументы верны для любого перехода из одного состояния в другое. Например, переход твердое тело — жидкость описывается кривыми, очень похо­жими на кривые фиг. 45.3 и 45.4.

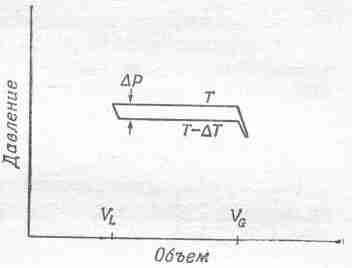
Фиг. 45.4. Диаграмма Р — V для цикла Карно с конденсирующимся в цилиндре паром.

Слева — все вещество переходит в жидкость. Чтобы полностью испарить ее при температуре Т, нужно добавить тепла L. При падении температуры от Т до Т—DT пар расширяется адиаба­тически.

Вводя скрытую теплоту плав­ления М/моль, мы получим формулу, аналогичную уравне­нию (45.14): (дP_пл/дT)_V=M/[T(V_L-V_S)]. Мы можем не знать ничего о кинетической теории процесса плавления, а все же получить правильное уравнение. Однако если мы узнаем кинетическую теорию, то сразу же получим большое пре­имущество. Уравнение (45.14) — это всего лишь дифферен­циальное уравнение, и мы еще совершенно не умеем находить постоянные интегрирования. В кинетической теории можно вычислить и эти постоянные, надо только придумать хорошую модель, описывающую все явление полностью. Итак, в каждой теории есть и хорошее, и плохое. Если познания наши слабы, а картина сложна, то термодинамические соотношения ока­зываются самым мощным средством. Когда же картина упро­щается настолько, что можно ее проанализировать теоретиче­ски, то лучше сначала попробовать выжать из этого анализа как можно больше.

Еще один пример: излучение черного тела. Мы уже гово­рили об ящике, содержащем излучение и ничего больше, и уже толковали о равновесии между излучением и осциллятором.

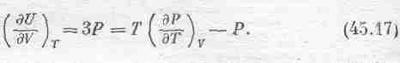
Мы выяснили также, что когда фотоны ударяются о стенки ящи­ка, они создают давление Р. Мы вывели формулу PV=U/3, где U — полная энергия фотонов, а V — объем ящика. Если под­ставить U=3РV в основное уравнение (45.7),то обнаружится, что

Поскольку объем ящика не изменяется, можно заменить (дP/дT)_{Vна dP/dT и получить обыкновенное дифференциальное уравне­ние. Оно легко интегрируется и дает lnP=4lnT+const, или Р=const·T⁴. Давление излучения изменяется как четвертая степень температуры, поэтому заключенная в излучении энер­гия U/V=P/3 тоже меняется как T⁴. Обычно пишут так: U/V=(4s/с)T⁴, где с — скорость света, а s— другая посто­янная. Термодинамика сама по себе ничего не скажет нам об этой постоянной. Это хороший пример и ее могущества, и ее бес­силия. Знать, что U/V изменяется как T⁴, — это уже большое дело, но узнать, чему именно равно U/V при той или иной тем­пературе, можно, только разобравшись в деталях полной тео­рии. У нас есть теория излучения черного тела и сейчас мы вы­числим а.}

Пусть I(w)dw — распределение интенсивности, иначе говоря, поток энергии через 1 м²за 1 сек в интервале частот между w и w+dw:

Распределение плотности энергии =

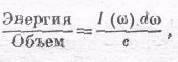
поэтому

U/V=Полная плотность энергии,

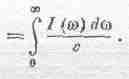
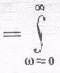(Плотность энергии между w и w+dw),

Мы уже успели узнать, что

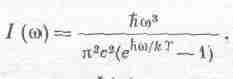
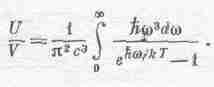
Подставляя выражение для I (w) в наше уравнение для U/V, получаем

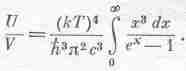
Если сделать замену переменных x=hw/kT, то это выраже­ние примет вид

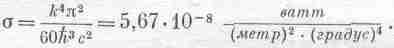
Этот интеграл — просто-напросто какое-то число, и мы можем найти его приближенно. Для этого надо лишь вычертить подын­тегральную кривую и подсчитать площадь под ней. Она прибли­зительно равна 6,5. Математики могут вычислить наш интеграл точно, он равен p⁴/15. Сравнивая это выражение с записан­ным ранее U/V=(4s/с)T⁴, мы найдем s:

Много ли энергии утечет за 1 сек из дырки единичной пло­щади, проделанной в стенке ящика? Чтобы найти поток энер­гии, умножим плотность энергии U/V на с. Еще нужно умножить на ¹/₄; эта четверть набегает вот по каким причинам. Во-первых, ^l/₂появляется из-за того, что мы вычисляем только вырвавшу­юся наружу энергию, и, во-вторых, если поток подходит к дыр­ке не под прямым углом, то вырваться ему труднее; это умень­шение эффективности учитывается умножением на косинус угла с нормалью. Среднее значение косинуса равно ¹/₂. Теперь понятно, почему мы писали U/V=(4s/c)T⁴: так проще выразить поток энергии сквозь маленькую дырку; если отнести поток к единичной площади, то он равен просто sT⁴.

* Поскольку (e^x-1)^-1 =е^-x+е^-2x +..., то интеграл равен

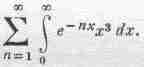
Но 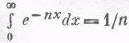, поэтому, дифференцируя три раза по n, мы получаем

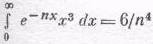, так что интеграл равен 6 (1+¹/₁₆+¹/₈₁+...), и несколько первых членов ряда дают уже хорошее приближение. В гл. 50 мы сможем показать, что сумма обратных четвертых степеней целых чисел равна p⁵/90.