6.3. Рост массы в зависимости от скорости

6.3. Рост массы в зависимости от скорости

Представление зависимости массы от скорости занимает особое положение в современной физике. История формирования соотношения между массой и энергией изложена В. В. Чешевым в работе [1], где, в частности, сказано: «Представление о возрастании массы электрона было отчасти инициировано гипотезой эфира. В 1881 году Дж. Дж. Томсон, исходя из теоретических соображений, указал, что «электрически заряженное тело из-за магнитного поля, которое оно вызывает, согласно теории Максвелла, так должно вести себя, как будто его масса увеличивается на некоторую величину, зависящую от его заряда и формы». В дальнейшем Томсон показал, что масса движущегося заряда должна возрастать с возрастанием его движения. Опыты Кауфмана закрепили представление о возрастании массы движущегося электрона» [1, c.117].

Первоначальное, неуверенное предположение Томсона о наблюдаемом «как будто» бы росте массы в настоящее время переросло в уверенность эквивалентности между массой и энергией, закрепленной в известной формуле Е = mc², где Е — энергия, m — масса. Для нашего же случая существенным является следующее замечание из цитируемой работы: «Результаты экспериментов Кауфмана наводят на мысль, что действие, оказываемое со стороны поля на движущийся заряд, отличается от его же действия на заряд покоящийся» [1, с. 117].

Это явление как будто проявляется при эксплуатации ускорителей заряженных частиц. Но в ускорителях заряженных частиц наблюдается не изменение массы частиц в зависимости от скорости (это наблюдать невозможно), а необъяснимое в современных физических представлениях изменение ускорения заряженных частиц при контролируемых электрическом и магнитном полях.

Из второго закона Ньютона a = F/m, где а — ускорение, F — сила, m — масса, видно, что ускорение зависит и от силы, и от массы. Поэтому более логичным представляется объяснение наблюдаемого ускорения не ростом массы, а результатом изменения сил взаимодействия электрического и магнитного полей с заряженными частицами, движущимися в этих полях.

Изменение сил взаимодействия определяется конечной скоростью распространения возмущения (изменения) напряженности полей. Неизменность сил взаимодействия при движении взаимодействующих тел возможна только в том случае, если скорость распространения возмущения бесконечна.

Рис. 20

Как бы быстро ни был перемещен заряд q в точку К электрического поля напряженностью Е (рис. 20), созданного заряженными пластинами В и Д, положение, показанное на рис. 21, может иметь место только через конечный интервал времени, определяемый скоростью распространения возмущения в поле Е.

Рис. 21

Полагаем, что взаимодействие поля с заряженной частицей в вакууме происходит со скоростью с, скоростью распространения электромагнитного поля, при этом сохраняется равенство импульса силы моменту количества движения. Тогда сила взаимодействия F (v) электрического поля напряженностью Е и частицы, имеющий заряд q и двигающийся в этом поле со скоростью v, будет равна:

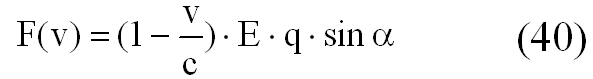
где ? — угол между векторами напряженности Е и скорости v.

Под воздействием ускоряющего поля возрастает скорость, а вместе с ней кинетическая энергия частицы. При этом происходит определенное изменение конфигурации ускоряющего поля и собственного поля ускоряемой частицы, которое приводит к увеличению ее потенциальной энергии, т. е. переходу потенциальной энергии ускоряющего поля в кинетическую энергию и потенциальную энергию ускоряемого заряда. Полная энергия частицы А, равная qU (U — пройденная разность потенциалов), слагается из ее кинетической энергии — E_k и потенциальной — Е_p

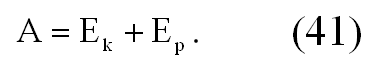
Кинетическая энергия ускоряемой частицы ограничена пределом

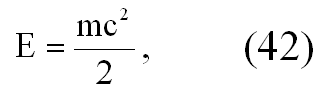
потенциальная же энергия ускоряемой частицы, возможно предела не имеет, пока не виден. Поэтому полная энергия ускоряемой частицы, несмотря на ограничение скорости, продолжает расти и определяется только пройденной разностью потенциалов. Данный процесс обратим, при взаимодействии разогнанной частицы с тормозящим полем происходит освобождение запасенной энергии.

Сила Лоренца — F (v), действующая на движущийся в магнитном поле заряд, определяется аналогичным образом:

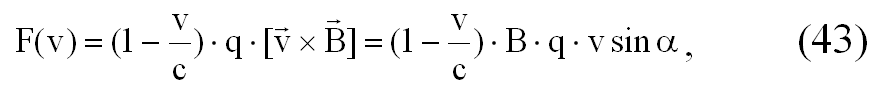
где В — индукция, ? — угол между направлениями скорости и индукции. Сила Лоренца направлена перпендикулярно к плоскости, в которой лежат векторы  B и v.