Как складывать скорости

Как складывать скорости

Если я ждал полчаса и еще час, то всего я потерял времени полтора часа. Если мне дали рубль, а затем еще два, то я всего получил три рубля. Если я купил 200 г винограда, а затем еще 400 г, то у меня будет 600 г винограда. Про время, массу и другие подобные величины говорят, что они складываются алгебраически.

Однако не всякие величины можно так просто складывать и вычитать. Если я скажу, что от Москвы до Коломны 100 км, а от Коломны до Каширы 40 км, то отсюда не следует, что Кашира находится от Москвы на расстоянии 140 км. Расстояния не складываются алгебраически.

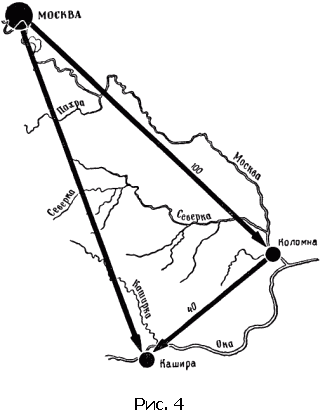
Как же еще можно складывать величины? На нашем примере мы легко найдем нужное правило. Нанесем на бумагу три точки, которые указывают взаимное расположение интересующих нас трех пунктов (рис. 4). На этих трех точках можно построить треугольник. Если две стороны его известны, то можно найти и третью. Для этого, однако, надо знать угол между двумя заданными отрезками.

Неизвестное расстояние находят следующим образом: отложим первый отрезок и из конца его по заданному направлению построим второй. Теперь соединим начало первого отрезка с концом второго. Искомый путь изобразится замыкающим отрезком.

Сложение описанным способом называется геометрическим, а величины, складываемые этим способом, называются векторами.

Для того чтобы отличить начало и конец отрезка, его снабжают стрелкой. Такой отрезок – вектор – указывает длину и направление.

Это правило применяется и при сложении нескольких векторов. Переходя из первой точки во вторую, из второй в третью и т.д., мы пройдем путь, который можно изобразить ломаной линией. Но к той же самой точке можно пройти прямо из отправного пункта. Этот отрезок, замыкающий многоугольник, и будет векторной суммой.

Векторный треугольник показывает, разумеется, и как вычитать один вектор из другого. Для этого проводят их из одной точки. Вектор, проведенный из конца второго в конец первого, и будет разностью векторов.

Кроме правила треугольника, можно пользоваться равноценным ему правилом параллелограмма (рис. 5).

Это правило требует построения параллелограмма на складывающихся векторах и проведения диагонали из их пересечения. На рисунке видно, что диагональ параллелограмма и есть замыкающая треугольника. Значит, оба правила одинаково пригодны.

Векторы используются для описания не только перемещений. Векторные величины встречаются в физике часто.

Рассмотрим, например, скорость движения. Скорость есть перемещение за единицу времени. Раз перемещение – вектор, то и скорость – вектор, смотрящий в ту же сторону. При движении по кривой линии направление перемещения все время изменяется. Как же ответить на вопрос о направлении скорости? Небольшой отрезок кривой направлен так же, как касательная. Поэтому перемещение и скорость тела в каждый данный момент направлены по касательной к линии движения.

Складывать и вычитать скорости по правилу векторов приходится во многих случаях. Необходимость в сложении скоростей возникает, когда тело участвует одновременно в двух движениях. Такие случаи нередки: человек идет по поезду и, кроме того, движется вместе с поездом; капля воды, стекающая по стеклу вагонного окна, движется вниз под действием веса и путешествует вместе с поездом; земной шар движется вокруг Солнца и вместе с Солнцем совершает движение по отношению к другим звездам. Во всех этих и других подобных случаях скорости складываются по правилу сложения векторов.

Если оба движения происходят вдоль одной линии, то векторное сложение превратится в обычное сложение, когда оба движения направлены в одну сторону, и в вычитание, когда движения противоположны.

А если движения происходят под углом? Тогда мы прибегнем к геометрическому сложению.

Если, переправляясь через быструю реку, вы будете держать руль поперек течения, вас снесет вниз. Лодка участвовала в двух движениях: поперек реки и вдоль реки. Суммарная скорость лодки показана на рис. 6.

Еще один пример. Как выглядит движение дождевой струи из окна поезда? Вы, наверное, наблюдали дождь из окон вагона. Даже в безветренную погоду он идет косо, так, как будто его отклоняет ветер, дующий в лоб паровозу (рис. 7).

Если погода безветренная, капля дождя падает вертикально вниз. Но за время падения капли вдоль окна поезд проходит изрядный путь, убегает от вертикали падения, поэтому дождь и кажется косым.

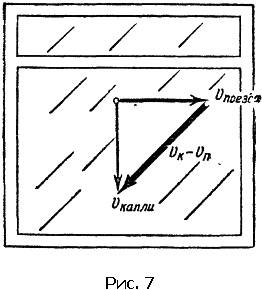
Если скорость поезда v_п, а скорость падения капли v_к, то скорость падения капли по отношению к пассажиру поезда получится векторным вычитанием v_п из v_к*4. Треугольник скоростей показан на рис. 7. Направление косого вектора указывает направление дождя; теперь ясно, почему мы видим дождь косым. Длина косой стрелки дает в выбранном масштабе величину этой скорости. Чем быстрее идет поезд и чем медленнее падает капля, тем более косыми покажутся нам дождевые струи.