Глава 6 ВЕРОЯТНОСТЬ
Глава 6
ВЕРОЯТНОСТЬ
Истинная логика нашего
мира—это подсчет
вероятностей.
Джемс Кларк Максвелл
§ 1. Вероятность и правдоподобие
§ 2. Флуктуации
§ 3. Случайные блуждания
§ 4. Распределение вероятностей
§ 5. Принцип неопределенности
§ 1. Вероятность и правдоподобие
«Вероятность», или «шанс»,— это слово вы слышите почти ежедневно. Вот по радио передают прогноз погоды на завтра: «Вероятно, будет дождь». Вы можете сказать: «У меня мало шансов дожить до ста лет». Ученые тоже часто употребляют эти слова. Сейсмолога интересует вопрос: какова вероятность того, что в следующем году в Южной Калифорнии произойдет землетрясение такой-то силы? Физик может спросить: с какой вероятностью этот счетчик Гейгера зарегистрирует двадцать импульсов в последующие десять секунд? Дипломата или государственного деятеля волнует вопрос: каковы шансы этого кандидата быть избранным президентом? Ну, а вас, конечно, интересует: есть ли шансы что-либо понять в этой главе?
Под вероятностью мы понимаем что-то вроде предположения или догадки. Но почему и когда мы гадаем? Это делается тогда, когда мы хотим вынести какое-то заключение или вывод, но не имеем достаточно информации или знаний, чтобы сделать вполне определенное заключение. Вот и приходится гадать: может быть, так, а может быть, и не так, но больше похоже на то, что именно так. Очень часто мы гадаем, когда нужно принять какое-то решение, например: «Брать ли мне сегодня с собой плащ или не стоит?» «На какую силу землетрясения должен я рассчитывать проектируемое здание?» «Нужно ли мне делать более надежную защиту?» «Следует ли мне менять свою позицию в предстоящих международных переговорах?» «Идти ли мне сегодня на лекцию?»
Иногда мы строим догадки потому, что хотим при ограниченности своих знаний сказать как можно больше о данной ситуации. В сущности ведь любое обобщение носит характер догадки. Любая физическая теория — это своего рода догадка. Но догадки тоже бывают разные: хорошие и плохие, близкие и далекие. Тому, как делать наилучшие догадки, учит нас теория вероятностей. Язык вероятностей позволяет нам количественно говорить о таких ситуациях, когда исход весьма и весьма неопределенен, но о котором все же в среднем можно что-то сказать.
Давайте рассмотрим классический пример с подбрасыванием монеты. Если монета «честная», то мы не можем знать наверняка, какой стороной она упадет. Однако мы предчувствуем, что ври большом числе бросаний число выпадений «орла» и «решки» должно быть приблизительно одинаковым. В этом случае говорят: вероятность выпадения «орла» равна половине.
Мы можем говорить о вероятности исхода только тех наблюдений, которые собираемся проделать в будущем. Под вероятностью данного частного результата наблюдения понимается ожидаемая нами наиболее правдоподобная доля исходов с данным результатом при некотором числе повторений наблюдения. Вообразите себе повторяющееся N раз наблюдение, например подбрасывание вверх монеты. Если NА — наша оценка наиболее правдоподобного числа выпадений с результатом А, например выпадений «орла», то под вероятностью Р(А) результата А мы понимаем отношение
P(A) =NA/N (6.1)
Наше определение требует некоторых комментариев. Прежде всего мы говорим о вероятности какого-то события только в том случае, если оно представляет собой возможный результат испытания, которое можно повторить. Но отнюдь не ясно, имеет ли смысл такой вопрос: какова вероятность того, что в этом доме поселилось привидение?
Вы, конечно, можете возразить, что никакая ситуация не может повториться в точности. Это верно. Каждое новое наблюдение должно происходить по крайней мере в другое время или в другом месте. По этому поводу я могу сказать только одно: необходимо, чтобы каждое «повторное» наблюдение казалось нам эквивалентным. Мы должны предполагать по крайней мере, что каждый новый результат наблюдения возник из равноценных начальных условий и из одного и того же уровня начальных знаний. Последнее особенно важно. (Если вы заглянули в карты противника, то, конечно, ваши прогнозы о шансах на выигрыш будут совсем другими, чем если бы вы играли честно!)
Хочу отметить, что я не собираюсь рассматривать значения N и NАв (6.1) только как результат каких-то действительных наблюдений. Число NА— это просто наилучшая оценка того, что могло бы произойти при воображаемых наблюдениях. Поэтому вероятность зависит от наших знаний и способностей быть пророком, в сущности от нашего здравого смысла! К счастью, здравый смысл не столь уже субъективен, как это кажется на первый взгляд. Здравым смыслом обладают многие люди, и их суждения о степени правдоподобия того или иного события в большинстве случаев совпадают. Однако вероятность все же не является «абсолютным» числом. Поскольку в каком-то смысле она зависит от степени нашего невежества, постольку с изменением наших знаний она может меняться.
Отмечу еще одну «субъективную» сторону нашего определения вероятности. Мы говорили, что NА — это «наша оценка наиболее вероятного числа случаев». При этом, конечно, мы не надеялись, что число нужных нам случаев будет в точности равно NА, но оно должно быть где-то близко к NA; это число более вероятно, чем любое другое. Если подбрасывать монету вверх 30 раз, то вряд ли можно ожидать, что число выпадений «орла» будет в точности 15; скорее это будет какое-то число около 15, может быть 12, 13, 14, 15, 16 или 17. Однако если необходимо выбрать из этих чисел какое-то одно число, то мы бы решили, что число 15 наиболее правдоподобно. Поэтому мы и пишем, что Р (орел) = 0,5.
Но почему все же число 15 более правдоподобно, чем все остальные? Можно рассуждать следующим образом: если наиболее вероятное число выпадений «орла» будет no, а полное число подбрасываний N, то наиболее вероятное число выпадений «решек» равно N-NO. (Ведь предполагается, что при каждом подбрасывании должны выпасть только либо «орел», либо «решка» и ничего другого!) Но если монета «честная», то нет основания думать, что число выпадений «орла», например, должно быть больше, чем выпадений «решки»? Так что до тех пор, пока у нас нет оснований сомневаться в честности подбрасывающего, мы должны считать, что Np=Nо, а следовательно, Np=no=N/2, или Р(орел) = P(решка) = 0,5.
Наши рассуждения можно обобщить на любую ситуацию, в которой возможны mразличных, но «равноценных» (т. е. равновероятных) результатов наблюдения. Если наблюдение может привести к mразличным результатам и ни к чему больше и если у нас нет оснований думать, что один из результатов предпочтительнее остальных, то вероятность каждого частного исхода наблюдения А будет 1/m, т. е. Р(А) = 1/m.
Пусть, например, в закрытом ящике находятся семь шаров разного цвета и мы наугад, т. е. не глядя, берем один из них. Вероятность того, что у нас в руке окажется красный шар, равна 1/7. Вероятность того, что мы из колоды в 36 карт вытащим даму пик, равна 1/36, такая же, как и выпадение двух шестерок при бросании двух игральных костей.
· · ·
В гл. 5 мы определяли размер ядра с помощью затеняемой им площади или так называемого эффективного сечения. По существу речь шла о вероятностях. Если мы «обстреливаем» быстрыми частицами тонкую пластинку вещества, то имеется некая вероятность, что они пройдут через нее, не задев ядер, однако с некоторой вероятностью они могут попасть в ядро. (Ведь ядра столь малы, что мы не можем видеть их, мы, следовательно, не можем прицелиться, и «стрельба» ведется вслепую.) Если в нашей пластинке имеется nатомов и ядро каждого из них затеняет площадь а, то полная площадь, затененная ядрами, будет равна na. При большом числе N случайных выстрелов мы ожидаем, что число попаданий NCбудет так относиться к полному числу выстрелов, как затененная ядрами площадь относится к полной площади пластинки:
NC/N=s/A. (6.2)
Поэтому можно сказать, что вероятность попадания каждой из выстреленных частиц в ядро при прохождении сквозь пластинку будет равна
РC =ns/A, (6.3)
где n/А — просто число атомов, приходящихся на единицу площади пластинки.
§ 2. Флуктуации
Теперь мне бы хотелось несколько подробнее показать, как можно использовать идею вероятности, чтобы ответить на вопрос: сколько же в самом деле я ожидаю выпадений «орла», если подбрасываю монету N раз? Однако, прежде чем ответить на него, давайте посмотрим, что все-таки дает нам такой «эксперимент». На фиг. 6.1 показаны результаты, полученные в первых трех сериях испытаний по 30 испытаний в каждой.

Фиг. 6.1. Последовательность выпадения «орла» и «решки».
Три серии опытов подбрасывания монеты по 30 раз в каждой серии.
Последовательности выпадений «орла» и «решки» показаны в том порядке, как это происходило. В первый раз получилось 11 выпадений «орла», во второй — тоже 11, а в третий — 16. Можно ли на этом основании подозревать, что монета была «нечестной»? Или, может быть, мы ошиблись, приняв 15 за наиболее вероятное число выпадений «орла» в каждой серии испытаний?
Сделаем еще 97 серий, т. е. 100 серий по 30 испытаний в каждой. Результаты их приведены в табл. 6.1.
Таблица б.1 · число выпадений «орла»
Проведено несколько серий испытаний, по 30 подбрасываний монеты в каждой
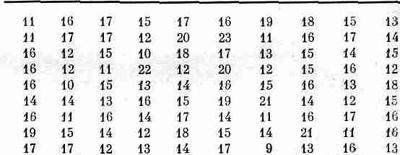
Взгляните на числа, приведенные в этой таблице. Вы видите, что большинство результатов «близки» к 15, так как почти все они расположены между 12 и 18. Чтобы лучше прочувствовать эти результаты, нарисуем график их распределения. Для этого подсчитаем число испытаний, в которых получилось k выпадений «орла», и отложим это число вверх над k. В результате получим фиг. 6.2.

Вертикальные линии показывают число серий, в которых выпадал k раз «орел». Пунктирная кривая показывает ожидаемое число серий с выпадением k раз «орла», полученное из вычисления вероятностей.
Действительно, в 13 сериях было получено 15 выпадений «орла», то же число серий дало 14 выпадений «орла»; 16 и 17 выпадений получались больше чем 13 раз. Должны ли мы из этого делать вывод, что монетам больше нравится ложиться «орлом» вверх? А может быть, мы неправы в выборе числа 15 как наиболее правдоподобного? Может быть, в действительности более правдоподобно, что за 30 испытаний получается 16 выпадений «орла»? Минуточку терпения! Если мы сложим вместе результаты всех серий, то общее число испытаний будет 3000, а общее число выпадений «орла» в этих испытаниях достигает 1492, так что доля испытаний с выпадением «орла» в результате будет 0,497. Это очень близко к половине, но все же несколько меньше. Нет, мы все-таки не можем предполагать, что вероятность выпадения «орла» больше, чем 0,5! Тот факт, что в отдельных испытаниях «орел» чаще выпадал 16 раз, чем 15, является просто случайным отклонением, или флуктуацией. Мы же по-прежнему ожидаем, что наиболее правдоподобным числом выпадений должно быть 15.
Можно спросить: а какова вероятность того, что в серии из 30 испытаний «орел» выпадет 15 раз или 16, или какое-то другое число раз? Мы говорим, что вероятность выпадения «орла» в серии из одного испытания равна 0,5; соответственно вероятность невыпадения тоже равна 0,5. В серии из двух испытаний возможны четыре исхода: ОО, OP, PO, PP. Так как каждый из них равновероятен, то можно заключить: а) вероятность двух выпадений «орла» равна 1/4; б) вероятность одного выпадения «орла» равна 1/4; в) вероятность невыпадения «орла» равна 1/4. Это происходит потому, что существуют две возможности из четырех равных получить одно выпадение «орла» и только одна возможность получить два выпадения или не получить ни одного.
Рассмотрим теперь серию из трех испытаний. Третье испытание с равной вероятностью может дать либо «орел», либо «решку», поэтому существует только один способ получения трех выпадений «орла»: мы должны получить два выпадения «орла» в двух первых испытаниях и затем выпадение «орла» в последнем. Однако получить два выпадения «орла» можно уже тремя способами: после двух выпадений «орла» может выпасть «решка» и еще два способа — после одного выпадения «орла» в первых двух испытаниях выпадет «орел» в третьем. Так что число равновероятных способов получить 3, 2, 1 и 0 выпадений «орла» будет соответственно равно 1, 3, 3 и 1; полное же число всех возможных способов равно 8. Таким образом, получаются следующие вероятности: 1/8. 3/8, 3/8, 1/8.
Эти результаты удобно записать в виде диаграммы (фиг. 6.3).
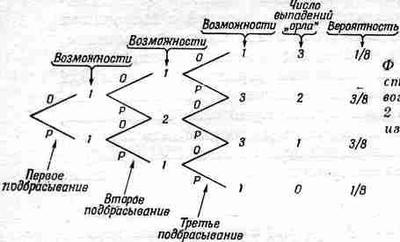
Фиг. 6.3. Диаграмма, иллюстрирующая число различных возможностей получения 0, 1, 2 и 3 выпадений «орла» в серии из трех испытаний.
Ясно, что эту диаграмму можно продолжить, если мы интересуемся еще большим числом испытаний. На фиг. 6.4 приведена аналогичная диаграмма для шести испытаний.
Фиг. 6.4. Диаграмма, подобная изображенной на фиг. 6.3, для серии из шести испытаний.
Число «способов», соответствующих каждой точке диаграммы,— это просто число различных «путей» (т. е., попросту говоря, последовательность выпадения «орла» и «решки»), которыми можно прийти в эту точку из начальной, не возвращаясь при этом назад, а высота этой точки дает общее число выпадений «орла». Этот набор чисел известен под названием треугольника Паскаля, а сами числа называются биномиальными коэффициентами, поскольку они появляются при разложении выражения (а+b)n, Обычно эти числа на нашей диаграмме обозначаются символом
(
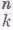 ), или Сnk(число сочетаний из n по k), где n— полное число
), или Сnk(число сочетаний из n по k), где n— полное число
испытаний, а k — число выпадений «орла». Отмечу попутно, что биномиальные коэффициенты можно вычислять по формуле
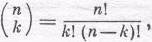 (6.4)
(6.4)
где символ п!, называемый «n-факториалом», обозначает произведение всех целых чисел от 1 до n, т. е. 1 · 2 · 3 . . . (n-1)·п. Теперь уже все готово для того, чтобы с помощью выражения (6.1) подсчитать вероятность Р (k, n) выпадения k раз «орла»! в серии из nиспытаний. Полное число всех возможностей будет 2" (поскольку в каждом испытании возможны два исхода), а число равновероятных комбинаций, в которых выпадет «орел», будет (
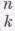 ) , так что
) , так что
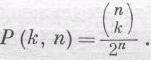 (6.5)
(6.5)
Поскольку Р (k, n) — доля тех серий испытаний, в которых выпадение «орла» ожидается k раз, то из ста серий k выпадений «орла» ожидается 100 Р (k, n) раз. Пунктирная кривая на фиг. 6.2 проведена как раз через точки функции 100 Р (k, 30). Видите, мы ожидали получить 15 выпадений «орла» в 14 или 15 сериях испытаний, а получили только в 13. Мы ожидали получить 16 выпадений «орла» в 13 или 14 сериях испытаний, а получили в 16. Но такие флуктуации вполне допускаются «правилами игры».
Использованный здесь метод можно применять и в более общей ситуации, где в каждом единичном испытании возможны только два исхода, которые давайте обозначим через В (выигрыш) и П (проигрыш). Вообще говоря, вероятности В и П в каждом отдельном испытании могут быть разными. Пусть р, например, будет вероятностью результата В. Тогда q (вероятность результата П) должна быть равна (1-р). В серии из nиспытаний вероятность того, что результат В получится k раз, равна
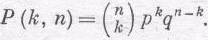 (6.6)
(6.6)
Эта функция вероятностей называется биномиальным законом распределения вероятности.
§ 3. Случайные блуждания
Существует еще одна интересная задача, при решении которой не обойтись без понятия вероятности. Это проблема «случайных блужданий». В простейшем варианте эта задача выглядит следующим образом. Вообразите себе игру, в которой игрок, начиная от точки х=0, за каждый ход может продвинуться либо вперед (до точки х), либо назад (до точки -х), причем решение о том, куда ему идти, принимается совершенно случайно, ну, например, с помощью подбрасывания монеты. Как описать результат такого движения? В более общей форме эта задача описывает движение атомов (или других частиц) в газе — так называемое броуновское движение — или образование ошибки при измерениях. Вы увидите, насколько проблема «случайных блужданий» тесно связана с описанным выше опытом с подбрасыванием монеты.
Прежде всего давайте рассмотрим несколько примеров случайных блужданий. Их можно описать «чистым» продвижением DNза N шагов. На фиг. 6.5 показаны три примера путей при случайном блуждании.
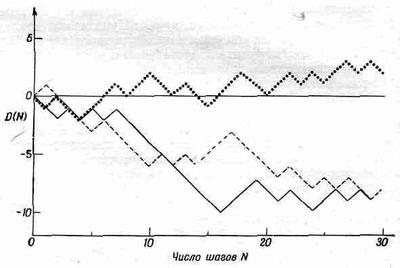
Фиг. 6.5. Три примера случайного блуждания.
По горизонтали отложено число шагов N, по вертикали — координата
D(N), т. е. чистое расстояние от начальной точки.
(При построении их в качестве случайной последовательности решений о том, куда сделать следующий шаг, использовались результаты подбрасывания монеты, приведенные на фиг. 6.1.)
Что можно сказать о таком движении? Ну, во-первых, можно спросить: как далеко мы в среднем продвинемся? Нужно ожидать, что среднего продвижения вообще не будет, поскольку мы с равной вероятностью можем идти как вперед, так и назад. Однако чувствуется, что с увеличением N мы все с большей вероятностью можем блуждать где-то все дальше и дальше от начальной точки. Поэтому возникает вопрос: каково среднее абсолютное расстояние, т. е. каково среднее значение D? Впрочем, удобнее иметь дело не с |D|, а с D2; эта величина положительна как для положительного, так и для отрицательного движения и поэтому тоже может служить разумной мерой таких случайных блужданий.
Можно показать, что ожидаемая величина D2Nравна просто N — числу сделанных шагов. Кстати, под «ожидаемой величиной» мы понимаем наиболее вероятное значение (угаданное наилучшим образом), о котором можно думать как об ожидаемом среднем значении большого числа повторяющихся процессов
блуждания. Эта величина обозначается как <D2N> и называется, кроме того, «средним квадратом расстояния». После одного
шага D2всегда равно +1, поэтому, несомненно, <D21> = 1. (За единицу расстояния всюду будет выбираться один шаг, и поэтому я в дальнейшем не буду писать единиц длины).
, Ожидаемая величина D2Nдля N>1 может быть получена из dn-1. Если после (N-1) шагов мы оказались на расстоянии DN-1, то еще один шаг даст либо DN=DN--1+1, либо DN=DN-1 -1. Или для квадратов
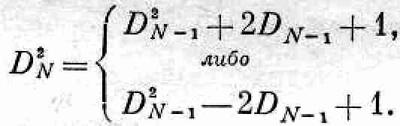
(6.7)
Если процесс повторяется большое число раз, то мы ожидаем, что каждая из этих возможностей осуществляется с вероятностью ?/2, так что средняя ожидаемая величина будет просто средним арифметическим этих значений, т. е. ожидаемая величина D2Nбудет просто D2N-1+1. Но какова величина D2N_1, вернее, какого значения ее мы ожидаем? Просто, по определению, ясно, что это должно быть «среднее ожидаемое значение» <D2N-1>, так что
<D2N>=<D2N-1+1. (6.8)
Если теперь вспомнить, что <D21>= 1, то получается очень простой результат:
<D2N>=N. (6.9)
Отклонение от начального положения можно характеризовать величиной типа расстояния (а не квадрата расстояния); для этого нужно просто извлечь квадратный корень из <.D2N> и получить так называемое «среднее квадратичное расстояние» DC-K:
DC-K=Ц<D2> = ЦN. (6.10)
Мы уже говорили, что случайные блуждания очень похожи на опыт с подбрасыванием монет, с которого мы начали эту главу. Если представить себе, что каждое продвижение вперед или назад обусловливается выпадением «орла» или «решки», то DNбудет просто равно No-NP, т. е. разности числа выпадений «орла» и «решки». Или поскольку No+Np=N(где N — полное число подбрасываний), то DN= 2No-N. Вспомните, что раньше мы уже получали выражение для ожидаемого распределения величины no[она обозначалась тогда через k; см. уравнение (6.5)]. Ну а поскольку N — просто постоянная, то теперь такое же распределение получил ось и для D. (Выпадение каждого «орла» означает невыпадение «решки», поэтому в связи между noи Dпоявляется множитель 2.) Таким образом, на фиг. 6.2 график представляет одновременно и распределение расстояний, на которые мы можем уйти за 30 случайных шагов k=15 соответствует D = 0, a k = 16 соответствует D= 2 и т. д.).
Отклонение no от ожидаемой величины N/2 будет равно
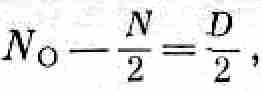
(6.11)
откуда для среднего квадратичного отклонения получаем
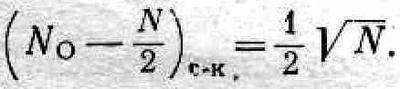
(6.12)
Вспомним теперь наш результат для dc-k. Мы ожидаем, что среднее расстояние, пройденное за 30 шагов, должно быть равно V30 = 5,5, откуда среднее отклонение k от 15 должно быть 5,5:2 = 2,8. Заметьте, что средняя полуширина нашей кривой на фиг. 6.2 (т. е. полуширина «колокола» где-то посредине) как раз приблизительно равна 3, что согласуется с этим результатом.
Теперь мы способны рассмотреть вопрос, которого избегали до сих пор. Как узнать, «честна» ли наша монета? Сейчас мы можем, по крайней мере частично, ответить на него. Если монета «честная», то мы ожидаем, что в половине случаев выпадет «орел», т. е.
<No>/N = 0,5. (6.13)
Одновременно ожидается, что действительное число выпадений «орла» должно отличаться от N/2на величину порядка ЦN/2, или, если говорить о доле отклонения, она равна
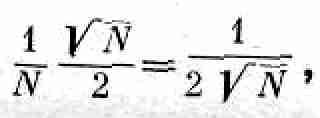
т. е. чем больше N, тем ближе к половине отношение No/N.
На фиг. 6.6 отложены числа NO/N для тех подбрасываний монеты, о которых мы говорили раньше.
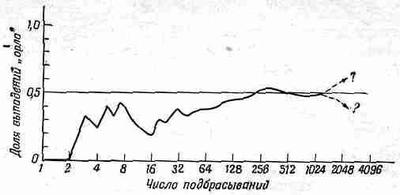
Фиг. 6.6. Доля выпадений «орла» в некоторой частной последовательности N подбрасываний монеты.
Как видите, при увеличении числа N кривая все ближе и ближе подходит к 0,5. Но, к сожалению, нет никаких гарантий, что для каждой данной серии или комбинации серий наблюдаемое отклонение будет близко к ожидаемому отклонению. Всегда есть конечная вероятность, что произойдет большая флуктуация — появление большого числа выпадений «орла» или «решки»,— которая даст произвольно большое отклонение. Единственное, что можно сказать,— это если отклонения близки к ожидаемому 1/2ЦN (скажем, со множителем 2 или 3), то нет оснований считать монету «поддельной» (или что партнер плутует).
Мы не рассматривали еще случаи, когда для монеты или какого-то другого объекта испытания, подобного монете (в том смысле, что возможны два или несколько достоверно не предсказуемых исхода наблюдения, например камень, который может упасть только на какую-то из двух сторон), имеется достаточно оснований полагать, что вероятности разных исходов не равны. Мы определили вероятность Р(O) как отношение <No>/N. Но что принять за величину <Nо>? Каким образом можно узнать, что ожидается? Во многих случаях самое лучшее, что можно сделать, это подсчитать число выпадений «орла» в большой серии испытаний и взять <No> =No (наблюденное). (Как можно ожидать чего-то еще?) При этом, однако, нужно понимать, что различные наблюдатели и различные серии испытаний могут дать другое значение P(О), отличное от нашего. Следует ожидать, однако, что все эти различные ответы не будут расходиться больше чем на 1/2ЦN [если Р(O)близко к половине], Физики-экспериментаторы обычно говорят, что «экспериментально найденная» вероятность имеет «ошибку», и записывают это в виде
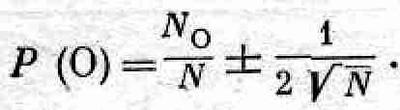
(6.14)
При такой записи подразумевается, что существует некая «истинная» вероятность, которую в принципе можно подсчитать, но что различные флуктуации приводят к ошибке при экспериментальном ее определении. Однако нет возможности сделать эти рассуждения логически согласованными. Лучше все-таки, чтобы вы поняли, что вероятность в каком-то смысле — вещь субъективная, что она всегда основывается на какой-то неопределенности наших познаний и величина ее колеблется при их изменении.
§ 4. Распределение вероятностей
Давайте вернемся к проблеме случайных блужданий, но теперь уже с некоторым изменением. Пусть в дополнение к случайному выбору направления шага (+ или -) некоторым непредсказуемым образом меняется также и его длина, причем требуется выполнение одного-единственного условия, чтобы длина шага в среднем была равна единице. Эта задача уже больше похожа на тепловое движение молекул в газе. Обозначим длину шага через S, которая, вообще говоря, может быть любой, но наиболее часто будет принимать значения где-то «вблизи» единицы. Для большей определенности давайте положим <S2>=1, или, что эквивалентно, SC-K= 1. Вывод выражения для <D2> при этом останется тем же, за исключением того, что уравнение (6.8) изменится теперь следующим образом:
<D2N>=<D2N-1>+<S2>=<D2N-1>+1. (6.15)
Так что, как и прежде,
<D2N>=N. (6.16)
Каково же в этом случае будет распределение расстояний! Какова, например, вероятность того, что после 30 шагов D окажется равным нулю? Вероятность этого равна нулю! Вообще вероятность любой заданной величины D равна нулю. Действительно, совершенно невероятно, чтобы сумма всех шагов назад (при произвольной длине каждого из них) в точности скомпенсировалась шагами вперед. В этом случае мы уже не можем построить график типа изображенного на фиг. 6.2.
Если же, однако, не требовать, чтобы D было в точности равно, скажем, нулю, или единице, или двум, а вместо этого говорить о вероятности получения D где-то вблизи нуля, или единицы, или двух, то при этом мы можем нарисовать график, подобный приведенному на фиг. 6.2. Назовем Р (х,Dx) вероятностью того, что D будет находиться где-то внутри интервала Dx в окрестности величины х (скажем, где-то между х и х+Dx). Если Ax достаточно мало, то вероятность того, что D попадет в этот интервал, должна быть пропорциональна его ширине, т. е. Ax. Поэтому мы можем утверждать, что
Р (х, Dx)=р(х)Dx;. (6.17)
Функция р(х) называется плотностью вероятности.
Вид кривой р(х) зависит как от числа шагов N, так и от распределения шагов по длинам (т. е. от того, какую долю составляют шаги данной длины). К сожалению, я не могу здесь заниматься доказательством этого, а только скажу, что при достаточно большом числе шагов N плотность p(х) одинакова для всех разумных распределений шагов по длинам и зависит лишь от самого N. На фиг. 6.7 показаны три графика р(х) для различных N.
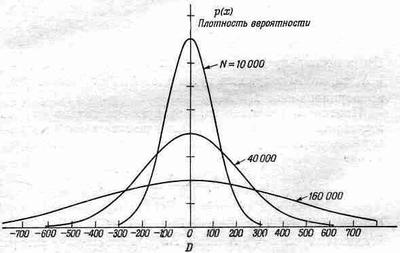
Фиг. 6.7. Плотность вероятности оказаться при случайном блуждании через N шагов на расстоянии D.
D измеряется в единицах средней квадратичной длины шага.
Заметьте, что «полуширины» этих кривых, как это и должно быть по нашим предыдущим расчетам, приблизительно равны Цn.
Вы, вероятно, заметили также, что величина р(х) вблизи нуля обратно пропорциональна ЦN. Это происходит потому, что все кривые по форме очень похожи, только одни «размазаны» больше, а другие — меньше, и, кроме того, площади, ограниченные каждой кривой и осью х, должны быть равны. Действительно, ведь р(х) Dx; это вероятность того, что D находится где-то внутри интервала Dx; (Ax мало). Как определить вероятность того, что D находится где-то между x1 и x2? Для этого разобьем интервал между х1и х2на узкие полоски шириной Ax; (фиг. 6.8) и вычислим сумму членов р (х) Dx; для каждой такой полоски.
Фиг. 6.8. Вероятность [заштрихованная область под кривой р(х)] того, что при случайном блуждании пройденное расстояние D окажется между х1 и х2.
Геометрически эта вероятность [запишем ее в виде Р (x1< D<x2)] равна площади заштрихованной области на фиг. 6.8. При этом чем уже будут наши полоски, тем точнее результат. Поэтому можно записать
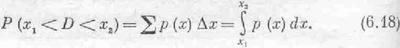
Площадь же ограничения всей кривой просто равна вероятности того, что D принимает какое-то значение между -Ґ и +Ґ. Ясно, что она должна быть равна единице, т. е.
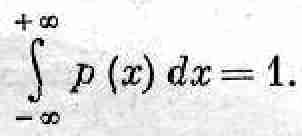
(6.19)
Ну а поскольку ширина кривых на фиг. 6.7 пропорциональна ЦN, то, чтобы сохранить ту же площадь, их высота должна быть пропорциональна 1/ЦN.
Плотность вероятности, которую мы только что описали, встречается наиболее часто. Она известна также под названием нормальной, или гауссовой, плотности вероятности и записывается в виде
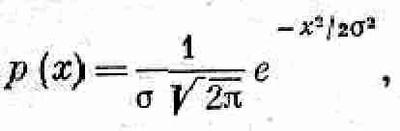
(6.20)
причем величина s называется стандартным отклонением.
В нашем случае s = ЦN или ЦNSc-k, если средняя квадратичная длина шага отлична от единицы.
Мы уже говорили о том, что движения молекул или каких-то других частиц в газе похожи на случайные блуждания. Представьте себе, что мы открыли в комнате пузырек с духами или каким-то другим органическим веществом. Тотчас же молекулы его начнут испаряться в воздух. Если в комнате есть какие-то воздушные течения, скажем циркуляция воздуха, то они будут переносить с собой пары этого вещества. Но даже в совершенно спокойном воздухе молекулы будут распространяться, пока не проникнут во все уголки комнаты. Это можно определить по запаху или цвету. Если нам известен средний размер «шага» и число шагов в секунду, то можно подсчитать вероятность обнаружения одной или нескольких молекул вещества на некотором расстоянии от пузырька через какой-то промежуток времени. С течением времени число шагов возрастает и газ «расползается» по комнате, подобно нашим кривым на фиг. 6.7. Длина шагов и их частота, как вы узнаете впоследствии, связаны с температурой и давлением воздуха в комнате.
Вы знаете, что давление газа вызывается тем, что молекулы его бомбардируют стенки сосуда. Позднее, когда мы подойдем к количественному описанию этого явления, нам понадобится знать, с какой скоростью движутся молекулы, ударяясь о стенку, поскольку сила их ударов зависит от скорости. Однако говорить о какой-то определенной скорости молекул совершенно невозможно. В этом случае необходимо использовать вероятностное описание. Молекула может иметь любую скорость, но некоторые скорости предпочтительнее других. Все происходящее в газе можно описать, сказав, что вероятность того, что данная молекула движется с какой-то скоростью между v и v+Dv, будет равна p(v)Dv, где р(v) — плотность вероятности, которая зависит от скорости v. Позднее я расскажу, как Максвелл, используя общие понятия и идеи теории вероятности, нашел математическое выражение для функции p(v). Примерный вид функции p(v) показан на фиг. 6.9.
???
Фиг. 6.9. Распределение молекул газа по скоростям.
Скорость может иметь любую величину, однако больше шансов за то, что она окажется где-то в окрестности наиболее вероятного или ожидаемого значения
<v>.
О кривой, показанной на фиг. 6.9, часто говорят в несколько ином смысле. Если мы возьмем газ, заключенный в каком-то сосуде (скажем, объемом 1 л), то окажется, что в нем имеется огромное количество молекул (N » 1022). Поскольку р(v)Dv — вероятность того, что первая попавшаяся молекула будет лететь со скоростью, находящейся в интервале Dv, то, по определению, ожидаемое число молекул <DN> со скоростью, находящейся в этом же интервале, будет равно
<DN>=Np(v) Dv. (6.21)
Поэтому Np (v) можно назвать «распределением молекул по скоростям». Площадь под кривой между двумя значениями скоростей vlи v2 [заштрихованная область на фиг. 6.9 для кривой Np(v)] представляет ожидаемое число молекул со скоростями между v1 и v2 . Но в газе, который содержит обычно огромное число молекул, отклонения от ожидаемого значения будут очень малы (порядка 1/ЦN), поэтому часто мы выбрасываем слово «ожидаемое» и говорим просто: «Число молекул со скоростями между v1и v2равно площади заштрихованного участка».Однако нужно все-таки помнить, что речь в таких случаях всегда идет о вероятном числе.
§ 5. Принцип неопределенности
Понятия вероятности оказались очень полезны при описании поведения газа, состоящего из огромного количества молекул. Немыслимо же в самом деле пытаться определить положение и скорость каждой из 1022 молекул! Когда впервые теория вероятности была применена к таким явлениям, то это рассматривалось просто как удобный способ работы в столь сложной обстановке. Однако теперь мы полагаем, что вероятность существенно необходима для описания различных атомных процессов. Согласно квантовой механике, этой математической теории малых частичек, при определении положения частички и ее скорости всегда существует некоторая неопределенность. В лучшем случае мы можем только сказать, что существует какая-то вероятность того, что частица находится вблизи точки х.
Для описания местоположения частицы можно ввести плотность вероятности р1 (х), так что p1 (x) Dx будет вероятностью того, что частица находится где-то между х и х+Dx. Если положение частицы установлено достаточно хорошо, то примерный вид функции P1(x) может иллюстрировать график, приведенный на фиг. 6.10, а.
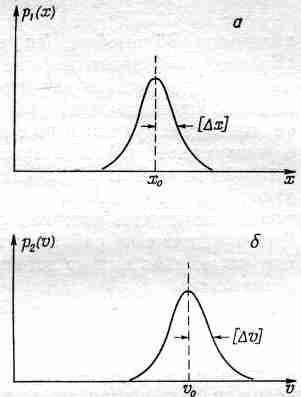
Фиг. 6.10. Плотности вероятности координаты, (а) и скорости (6) частицы.
Точно такое же положение и со скоростью частицы: она тоже неизвестна нам точно. С некоторой вероятностью р2 (v) Dvчастица может двигаться со скоростью, находящейся в интервале между v и v+Dv.
Один из основных результатов квантовой механики состоит в том, что эти две плотности р1 (х) и р2 (v) не могут быть выбраны независимо в том смысле, что они обе не могут быть сколь угодно узкими. Если мы возьмем «полуширины» кривых p1(х) и p2(v) и обозначим их соответственно [Dx] и [Dv] (см. фиг. 6.10), то природа требует, чтобы произведение этих двух полуширив было не меньше величины h/m, где m — масса частицы, a h — некоторая фундаментальная физическая постоянная, называемая постоянной Планка. Это соотношение записывается следующим образом:
[Dx][Dv]>=h/m (6.22)
и называется принципом неопределенности Гейзенберга.
Чтобы это соотношение выполнялось, частица должна себя вести очень курьезно. Вы видите, что правая часть соотношения (6.22) постоянна, а это означает, что если мы попытаемся «приколоть» частицу в каком-то определенном месте, то эта попытка окончится тем, что мы не сможем угадать, куда она летит и с какой скоростью. Точно также если мы попытаемся заставить частицу двигаться очень медленно или с какой-то определенной скоростью, то она будет «расплываться», и мы не сможем точно указать, где она находится.
Принцип неопределенности выражает ту неясность, которая должна существовать при любой попытке описания природы. Наиболее точное и полное описание природы должно быть только вероятностным. Однако некоторым физикам такой способ описания приходится не по душе. Им кажется, что о реальном поведении частицы можно говорить только, когда одновременно заданы импульсы и координаты. В свое время на заре развития квантовой механики эта проблема очень сильно волновала Эйнштейна. Он часто качал головой и говорил: «Но ведь не гадает же господь бог «орел — решка», чтобы решить, куда должен двигаться электрон!» Этот вопрос беспокоил его в течение очень долгого времени, и до конца своих дней он, по-видимому, так и не смог примириться с тем фактом, что вероятностное описание природы — это максимум того, на что мы пока способны. Есть физики, которые интуитивно чувствуют, что наш мир можно описать как-то по-другому, что можно исключить эти неопределенности в поведении частиц. Они продолжают работать над этой проблемой, но до сих пор ни один из них не добился сколько-нибудь существенного результата.
Эта присущая миру неопределенность в определении положения частицы является наиболее важной чертой описания структуры атомов. В атоме водорода, например, который состоит из одного протона, образующего ядро, и электрона, находящегося где-то вне его, неопределенность в местонахождении электрона такая же, как и размеры самого атома! Мы не можем поэтому с уверенностью сказать, где, в какой части атома находится наш электрон, и уж, конечно, не может быть и речи ни о каких «орбитах». С уверенностью можно говорить только о вероятности p(r)DV обнаружить электрон в элементе объема DV на расстоянии rот протона. Квантовая механика позволяет в этом случае вычислять плотности вероятности p(r), которая для невозмущенного атома водорода равна
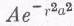 .
.
Это— колоколообразная функция наподобие изображенной на фиг. 6.8, причем число а представляет собой характерную величину радиуса, после которого функция очень быстро убывает. Несмотря на то что существует вероятность (хотя и небольшая) обнаружить электрон на большем, чем а, расстоянии от ядра, мы называем эту величину «радиусом атома». Она равна приблизительно 10-10м.
Если вы хотите как-то представить себе атом водорода, то вообразите этакое «облако», плотность которого пропорциональна плотности вероятности. Пример такого облака показан на фиг. 6.11.

Фиг. 6,11, Воображаемый атом водорода.
Плотность («белизна») облачка пропорциональна плотности вероятности обнаружения электрона.
Такая наглядная картинка, пожалуй, наиболее близка к истине, хотя тут же нужно помнить, что это не реальное «электронное облако», а только «облако вероятностей». Где-то внутри него находится электрон, но природа позволяет нам только гадать, где же именно он находится.
В своем стремлении узнать о природе вещей как можно больше современная физика обнаружила, что существуют вещи, познать которые точно ей никогда не удастся. Многому из наших знаний суждено навсегда остаться неопределенным. Нам дано знать только вероятности.
* Максвелл получил выражение p(v)=
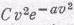 , где а — некоторая связанная с температурой постоянная, а С выбирается таким образом, чтобы полная вероятность была равна единице.
, где а — некоторая связанная с температурой постоянная, а С выбирается таким образом, чтобы полная вероятность была равна единице.
* Эти последние 97 экспериментов проводились следующим образом. Ящик, в котором находились 30 монет, энергично встряхивался; затем подсчитывалось число выпадений «орла».
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
Глава 6 ВЕРОЯТНОСТЬ
Глава 6 ВЕРОЯТНОСТЬ Истинная логика нашегомира—это подсчетвероятностей.Джемс Кларк Максвелл§ 1. Вероятность и правдоподобие§ 2. Флуктуации§ 3. Случайные блуждания§ 4. Распределение вероятностей§ 5. Принцип неопределенности§ 1. Вероятность и правдоподобие«Вероятность»,
Глава 2
Глава 2 Огненный дух «земного электричества»Открытия Гальвани и Вольты никого не оставили равнодушным. Ведь подумать только, без всяких движущихся механических частей, на одном таинственном химическом процессе можно создать источник электрической силы! Такой простой
Глава 3
Глава 3 Великое открытиеС самого момента открытия Эрстедом влияния электрического тока на магнитную стрелку исследователей стала преследовать мысль: «А нельзя ли решить и обратную задачу: превратить магнетизм в электричество?» Во Франции над этой задачей ломали голову
Глава 4
Глава 4 «Русский свет»«Применение электрической энергии в России за последние годы значительно развилось, электротехническая же промышленность в ней до последнего времени находится в младенческом возрасте». Это строчки из толстой книги профессора Артура Вильке
Глава 2
Глава 2 Время свершенийСегодня много говорят о получении энергии с помощью Солнца, ветра, морских волн, об извлечении энергии из недр, за счет использования внутреннего тепла Земли, о приручении морских приливов и о выведении электростанций за пределы атмосферы. Но пока…
Новая вероятность
Новая вероятность Новая вероятность принципиально отличалась от той, которую Максвелл положил в основу статистической физики, а Эйнштейн применил в задаче броуновского движения. Там речь шла об учете огромного числа факторов — например, толчков множества молекул. В
Вероятность грозы: только в облаках
Вероятность грозы: только в облаках Данный прогноз верен везде и всегда, поскольку высотные ветры повсеместно удерживают облака.Теперь немного подробностей.Максимальная и минимальная температуры на Венере совпадают ввиду плотности атмосферы и формы ее перемещения,
Глава 17
Глава 17 Получасом раньше, в тот самый момент, когда в класс Лазурро вбежал полковник, Миртиль поняла, что для их городка наступили последние часы.— Они нас нашли, — твердо сказал полковник. — Они уже здесь. Миртиль, Тристам, идемте со мной, вы должны бежать.Миртиль
Глава 18
Глава 18 Воздушный мотоцикл плыл совсем невысоко, в десяти метрах над облаком. Далеко внизу Том и Тристам различали берега вулканического острова.— Не стрелять! — повторил военный в плаще. — А тех — задержать!Солдаты высыпали на причал и начали обстреливать стрекозу
Глава 8
Глава 8 С прохладным и сыроватым рассветным воздухом смешивался густой дым, валивший из печных труб. На всех перекрестках в центре Белой Столицы были расставлены люди снегобоя. Они походили не столько на стражей порядка, сколько на оккупационные войска.Тристам и Том в
Глава 9
Глава 9 Наступила ночь, за окнами стояла глубокая тишина. Тристам уснул. Рядом с ним, с раскрытой книгой на животе, спал, погруженный в грезы о будущем, Том.В глубине комнаты, растянувшись на матрасе, храпел один из полицейских. Второй сидел на лесенке, стоявшей теперь возле
Глава 10
Глава 10 Тристам внимательно следил за тенью. Она двигалась прямо на военный патруль.«Там ему не проскочить!» — забеспокоился Тристам.Но человек с рюкзаком, наверное, и сам это знал: он вскарабкался по стене и, словно черная кошка, перепрыгивая с крыши на крышу, за считанные
Глава 11
Глава 11 Наутро, как только мальчики проснулись, полицейские повели их вниз, в подземный ход. К счастью, в тесном тоннеле, по которому пришлось продвигаться гуськом, было чисто и сухо.— Долго еще? — спросил Тристам, когда они прошли метров десять.— Тс-с! — шепнул